AcWing 4210. 数字

题目描述
给定一个大于 2 的十进制正整数 A。
该数字在 2∼A−1 进制表示下的各位数字之和均可以求出。
例如，数字 123 在 16 进制表示下，共有 2 位：第 1 位是 7，第二位是 11，各位数字之和为 18。
现在，请你将 A 在 2∼A−1 进制表示下的各位数字之和全部相加，并将得到的结果除以 A−2，最终结果以最简分数形式输出。

输入格式
一个十进制正整数 A。

输出格式
输出格式为 X/Y，其中 X 表示输出答案的分子，Y 表示输出答案的分母。

数据范围
前三个测试点满足 3≤A≤10。
所有测试点满足 3≤A≤1000。

输入样例1：

5

输出样例1：

7/3

输入样例2：

3

输出样例2：

2/1

解题思路
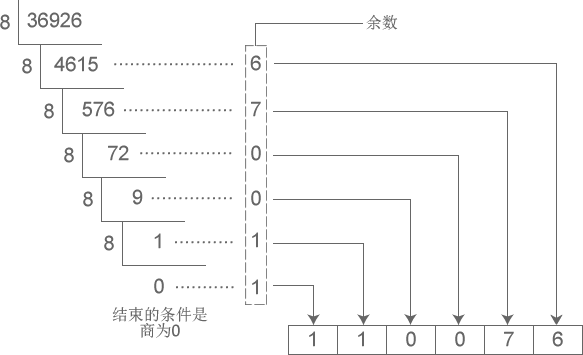
题不难，打卡记忆一下进制转换和辗转相除求最大公约数

代码

#include<iostream>
using namespace std;
int ab(int num, int ni) {int sumi = 0;do{sumi += (num % ni);num /= ni;} while (num != 0);return sumi;
}
int gcd(int m, int n) {if(m % n == 0){return n;}else{return gcd(n, m % n);}
}
int main() {int num;int sum = 0;cin >> num;for (int i = 2; i < num; ++i) {sum += ab(num, i);}int tmp = gcd(sum, num - 2);cout << sum / tmp << "/" << (num - 2) / tmp;}