一、求传递函数表达式residue()
1、极点不同的情况
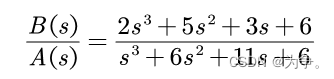
分子和分母的矩阵分别为:
>> num=[2 5 3 6];
>> den=[1 6 11 6];
使用下列命令,即可对分式进行展开,展开后有多项,每一项的分子一定是数字,而分母则是一个多项式,r称为留数,p称为级数,k称为单独项
>> [r,p,k]=residue(num,den)
2、根据分式展开式得到多项式
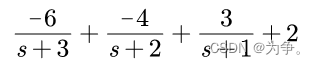
>> r=[-6 -4 3];
>> p=[-3 -2 -1];
>> k=2;
>> [num1,num2]=residue(r,p,k);
>> printsys(num1,num2,'s')
3、极数相等的情况
上边的例子都是分母极数不相等的,所以分母都是一次多项式,但如果考虑到另一种情况,分母也称为特征多项式,这个多项式有重根。
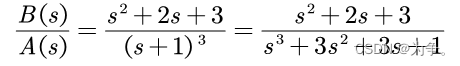
>> num1=[0 1 2 3];
>> num2=[1 3 3 1];
>> [r,p,k]=residue(num1,num2)
可以看到p的数值有三个,且相同,那么分母将不是一次多项式,而是

得到原函数
>> [num1,num2]=residue(r,p,k)
>> printsys(num1,num2,'s')
二、求传递函数的零点、极点以及增益K
格式:[z,p,k]=tf2zp(num,den)
z代表零点,p代表极点,k代表增益
例题1:

>> num=[0 4 16 12];
>> den=[1 12 44 48];
>> [z,p,k]=tf2zp(num,den)
如果已经给定零点、极点和增益,可以使用如下代码生成原来的函数
>> z=[-3;-1];
>> p=[-6;-4;-2];
>> k=4;
>> [num,den]=zp2tf(z,p,k);
>> printsys(num,den,'s')
三、有理假分式展开、求留数、极点和直接项
所谓有理假分式,就是分子的阶数比分母高,这就导致了有理假分式进行分式展开时含有直接项
例题1:求以下式子的的拉普拉斯逆变换
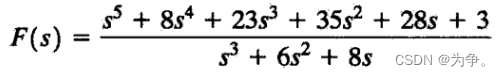
>> num=[1 8 23 35 28 3];
>> den=[1 6 8 0];
>> [r,p,k]=residue(num,den)
可以求出展开式:
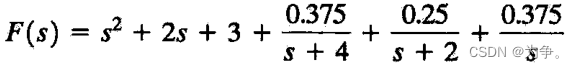
四、给定传递函数的零点、极点以及增益K求原传递函数
tf2zp:根据传递函数的分子分母来求得传递函数的零点、极点以及增益K
zp2tf:根据零点、极点和增益K求取传递函数
五、使用roots命令解多项式的根以及使用poly命令得到原多项式
例题1:
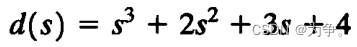
>> clear all
>> d=[1 2 3 4];
>> r=roots(d)
如果已经有原方程的根,则使用命令poly可以生成原多项式的系数
>> poly(r)
六、使用ord2命令生成一个标准的二阶系统
标准的二阶系统:
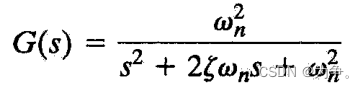
ord2命令能够生成一个二阶系统,但是分子部分没有常数的平方,所以需要乘一个系数
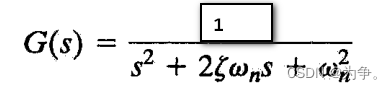
例子:![]()
>> wn=5;
>> damping_ratio=0.4;
>> [num0,den]=ord2(wn,damping_ratio)
>> printsys(num0,den,'s')
七、求传递函数的单位阶跃响应并绘制出曲线
如果传递函数的分子和分母都是已知的,可以通过tf命令来定义传递函数
>> sys=tf(num,den)
num和den分别是传递函数的分子和分母系数,使用step函数来求出响应曲线
>> step(sys)
或者
>> step(num,den)
例题1:
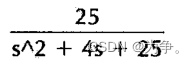
>> num=[25];
>> den=[1 4 25];
>> step(num,den)
八、求传递函数的奈奎斯特曲线
直接绘图
>> num=[0.5];
>> den=[1 2 1 0.5];
>> sys=tf(num,den)
>> nyquist(sys)
在图上显示幅值裕度和相角裕度
>> [Gm,Pm,Wcg,Wcp]=margin(sys)
>> nyquist(sys)
>> title(['Gm=',num2str(Gm),',','Pm=',num2str(Pm)])
九、求传递函数的伯德图
例子:

其中伯德图包括幅频特性曲线和相频特性曲线
1、在10的-1次幂和10的3次幂之间生成200个点:
>> w=logspace(-1,3,200);
2、分子多项式系数:
>> num=5*[0.1 1];
3、分子是一个简单的多项式乘积,使用卷积命令conv来求乘积后的多项式系数
>> f1=[1 0];
>> f2=[0.5 1];
>> f3=[1/2500 0.6/50 1];
>> den=conv(f1,conv(f2,f3));
4、绘制伯德图
>> sys=tf(num,den)
>> bode(sys,w)
十、利用margin求幅值裕度和相角裕度

>> num=[0.5];
>> den=[1 2 1 0.5];
>> sys=tf(num,den);
>> margin(sys)
返回参数不绘图
1、直接使用传递函数求
>> [Gm,Pm,Wcg,Wcp] = margin(sys)
2、利用伯德图返回的参数求
>> [mag,phase,w] = bode(sys)
>> [Gm,Pm,Wcg,Wcp] = margin(mag,phase,w)
十一、根轨迹绘制
某系统的开环传递函数如下,求根轨迹

>> num=[1,2,4];
>> den=conv(conv([1,4,0],[1,6]),[1,1.4,1]);
>> sys=tf(num,den);
>> rlocus(sys) //绘制根轨迹
>> axis([-8 2 -6 6]) //设定坐标范围,实轴[-8 2] 虚轴[-6 6]
在分析系统性能时,除了某一点对应的根轨迹增益外,有时还需要知道该增益对应的其他闭环极点的值,这时候输入以下命令:
>> [k,p]=rlocfind(sys)
十二、已知闭环传递函数求开环传递函数
开环传递函数=feedback(闭环传递函数,-1)
闭环传递函数=feedback(开环传递函数,1)
十三、求解微分方程的解
dsolve(‘方程1’,‘方程2’,…,‘方程n’,‘初始条件’,‘自变量’),
初始条件省缺时,是求微分方程的通解。
Dy代表y的导数,D2y代表y的二阶导数, D3y代表y的三阶导数……
例题1:
![]()
>> y=dsolve('D2y+2*Dy+y-x^2=0','x')
例题2:

>> y1=dsolve('D2y+4*Dy+29*y=0','y(0)=0,Dy(0)=15','x')
例题3:
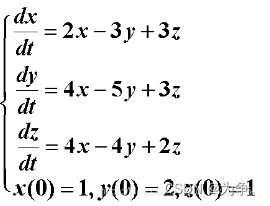
>> eq1='Dx=2*x-3*y+3*z';
>> eq2='Dy=4*x-5*y+3*z';
>> eq3='Dz=4*x-4*y+2*z';
>> [x,y,z]=dsolve(eq1,eq2,eq3,'x(0)=1,y(0)=2,z(0)=1')
十四、泰勒展开
1、求公式f的麦克劳林多项式
格式:taylor(f)
2、求公式f在x=1处的泰勒级数展开
格式:taylor(f,x,’EspansionPoint’,1)
格式:taylor(f,x,1)
3、求函数f的泰勒多项式的n项目
格式:taylor(f,’order’,4)
4、求函数f在x=n处的a阶多项式
格式:taylor(f,x,n,’order’,a)
5、画出展开式的图
ezplot(ans)
十五、状态空间表达式建立
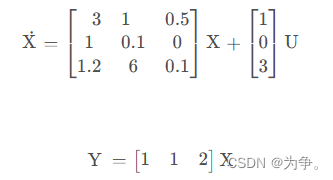
>> A=[3,1,0.5;1 0.1 0;1.2 6 0.1]
>> B=[1;0;3]
>> C=[1 1 2]
>> D=0
>> sys=ss(A,B,C,D) //建立状态空间表达式模型
>> sys=tf(sys) //得到系统多项式形式的传递函数模型
>> sys=zpk(sys) //得到系统零-极点形式的传递函数模型
>> [num,den]=ss2tf(A,B,C,D) //传递函数多项式形式的分子、分母多项式系数
>> [A,B,C,D]=tf2ss(num,den) //与上边的式子反过来
>> [z,p,k]=ss2zp(A,B,C,D) //得到极点、零点、增益
>> [A,B,C,D]=zp2ss(z,p,k) //跟上边的式子反过来
十六、判断系统稳定性
eig函数:直接判定
pzmap函数:图解判定
1、高阶连续系统稳定性的判断
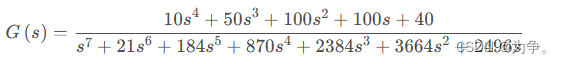
>> num=[10 50 100 100 40];
>> den=[1 21 184 870 2384 3664 2496];
>> sys=tf(num,den);
>> sys1=feedback(sys,1) //求系统单位反馈传递函数
>> pzmap(sys1) //绘制零极点图
>> eig(sys1) //求系统特征根
2、高阶离散系统稳定性判断
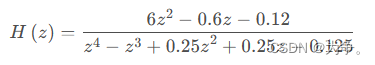
>> num=[6 -0.6 -0.12];
>> den=[1 -1 0.25 0.25 -0.125];
>> sys=tf(num,den,'Ts',0.1)
>> z=tf('z','Ts',0.1)
>> Gc=0.3*(z-0.6)/(z+0.8);
>> sys1=feedback(sys*Gc,1)
>> pzmap(sys1),abs(eig(sys1)')
十七、傅里叶变换
1、傅里叶变换
>> syms x w
>> f=exp(-x^2);
>> g=fourier(f,w)
2、傅里叶逆变换
>> syms x w
>> f=exp(-w^2/4);
>> g=ifourier(f,x)
十八、拉普拉斯变换
1、拉普拉斯变换
例题1:
![]()
>> syms t;
>> x=t*exp(-2*t);
>> X=laplace(x);
>> disp(X)
例题2:
![]()
>> syms t;
>> x=exp(-t)*sin(2*t);
>> X=laplace(x);
>> disp(X)
2、拉普拉斯逆变换
例题1:
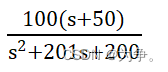
>> syms s;
>> F=100*(s+50)/(s^2+201*s+200);
>> f=ilaplace(F);
>> disp(F)
>> ezplot(f)
例题2:
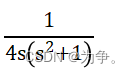
>> syms s;
>> F=1/(4*s*(s^2+1));
>> f=ilaplace(F);
>> disp(f)
>> ezplot(f)
整理自
一:用MATLAB求传递函数的零点,极点以及增益K_Mr.YunLong的博客-CSDN博客_matlab求传递函数零极点
MATLAB学习记录-传递函数的建模2(零-极点形式的传递函数模型)-自动控制篇_Blablabla...的博客-CSDN博客_zp2tf函数
MATLAB学习记录-传递函数的建模1(多项式形式的传递函数模型)-自动控制篇_Blablabla...的博客-CSDN博客_传递函数的分子分母系数