目录
一、递归的定义
1、什么时候会用到递归的方法
1. 定义是递归的
2. 数据结构是递归的
3. 问题的解法是递归的
2、应用递归的原则
3、递归调用顺序问题
1. 首先递归的过程可以总结为以下几点:
2. 递归工作栈
二、 递归和非递归的转化
1. 单向递归可用迭代
举例:斐波拉契数列
2. 尾递归可用迭代
举例:欧几里德求最大公约数
3. 借助栈实现非递归
1. 举例:二叉树的先序遍历
2. 举例:二叉树的中序遍历
三、分治解题步骤
四、汉诺塔问题
1. 问题
2. 解题思路
3. 两个盘子演示
4. 三个盘子演示
5. 四个盘子演示
6. 代码
一、递归的定义
- 在数学及程序设计方法学中为递归下的定义是这样的:若一个对象部分包含地包含它自己,或用它自己来定义它自己,则称这个对象是递归的;若一个过程直接或间接的调用自己,则称这个过程为递归的过程。
- 简而言之,递归方法就是直接或间接地调用其自身
1、什么时候会用到递归的方法
1. 定义是递归的
- 以数学上常用的阶乘函数为例,其定义和计算都是递归的
定义:
求解函数:
int faction(int n)
{if (n == 1)return 1;elsen = faction(n - 1) * n;return n;}2. 数据结构是递归的
- 链表就是一种递归的数据结构,从概念上讲,单链表可以递归的定义为一个结点,当该结点的指针域为NULL的时候,就表明此链表是一个单链表,这个结点的指针域也可以指向另一个单链表,而这个单链表具有同样的结构
- 树也可以采用递归的方式来描述。首先一棵树要么是空,要么由若干非空子树组成(子树的数目可以为空),且这些子树的根都通过一条边连到根上。每个子树同样具有这样的结构,要么为空,要么由根和若干非空子树组成。
3. 问题的解法是递归的
2、应用递归的原则
- 首先是必须要有一些“基本条件”能够采用非递归的方式计算得到,这是使用递归方法的重要前提。基本条件的满足意味着采用递归处理后的子问题可以直接解决时,就停止分解,而这些可以直接求解的问题就叫做递归的“基本条件”。
- 为了使计算最终完结,任何递归调用都要朝着“基本条件”的方向进行。
- 例1:前面所举例的阶乘
if (n == 1)return 1;这就是所谓的基本条件。
- 例2:二分查找(折半查找)
int BinSearch(int* data, int key,int low,int high)//折半查找
{if (low > high)return -1;int mid = (low + high) / 2;//二分查找递归的核心部分if (key < data[mid])return(data, key, low, mid - 1);//继续在data[low,mid-1]左区间查找else if (key > data[mid])return(data, key, mid + 1, high);//继续在data[mid+1,high]右区间查找elsereturn mid;//查找成功
}- 其中:if(low>high)是基本条件之一,即在搜索范围内无法找到想要查找的值,表示搜索失败,递归过程也就结束了;此外,找到想要查找的值递归过程也会结束,也就是“return mid”,其对应的条件是“if(key==data[mid]”。
3、递归调用顺序问题
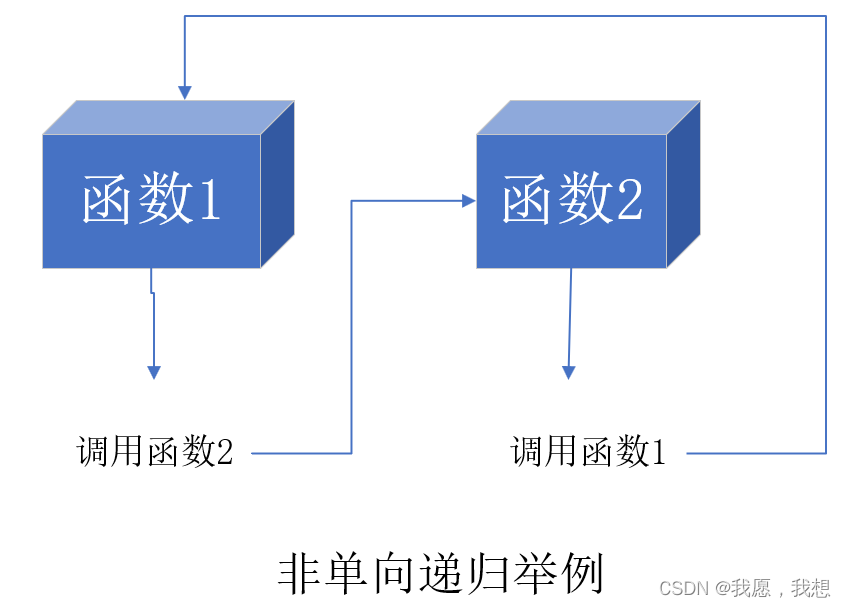
1. 首先递归的过程可以总结为以下几点:
- 递归过程在实现时,需要自己调用自己
- 层层向下递归,退出次序正好相反
- 主程序第一次递归调用自己为内部调用
- 它们返回调用它的过程的地址不同
2. 递归工作栈
- 在递归过程中,递归的执行需要一些薄记空间来记录跟踪前一个递归调用,特别对于那些有一长串递归调用的情况,在某种程度上较同等循环而言更加费时,因为薄记工作本身就要消耗一定时间。这个薄记空间就是递归工作栈。
- 同时,每一次递归调用时,需要为过程中使用的参数、局部变量等另外分配存储空间。
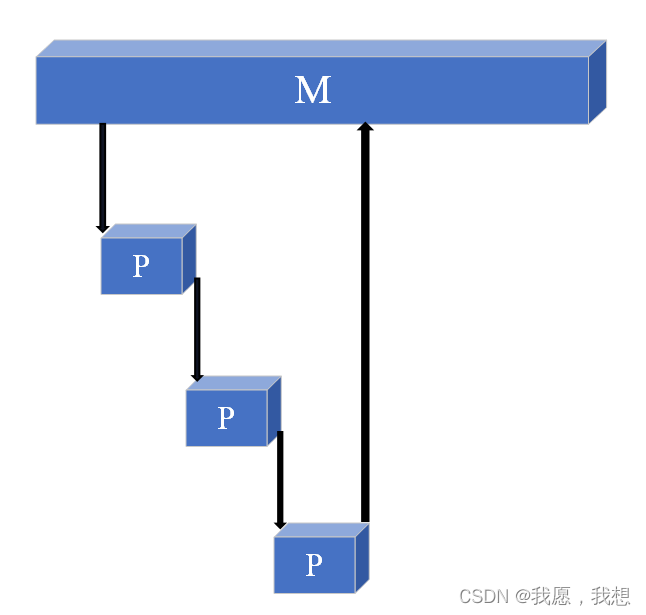
- 每层递归调用需分配函数递归时的活动记录 可以用如下图表示:

- 以下列代码为例:
#include<iostream>
using namespace std;
void Fuction1(int n)
{if (n < 4){printf("%d\n", n);Fuction1(n + 1);}
}
void Fuction2(int n)
{if (n < 4){Fuction2(n + 1);printf("%d\n", n);}
}
int main()
{cout << "第一个函数:" << endl;Fuction1(0);cout << "第二个函数:" << endl;Fuction2(0);return 0;
}- Fuction1函数的执行过程

- Fuction2函数执行过程:
二、 递归和非递归的转化
1. 单向递归可用迭代
- 单向递归: 是指递归的过程总是朝着一个方向进行。斐波拉契数列的求解就是单向递归
-
举例:斐波拉契数列
- 递归求解斐波拉契数列:
int Fib(int n)
{if (n < 2)return n == 0 ? 0 : 1;else if (n >= 2){n = Fib(n - 1) + Fib(n - 2);return n;}
}- 迭代求解斐波拉契数列:
int Fib(int n)
{vector<int> v;v.push_back(0);v.push_back(1);int i = 2;for (i = 2; i <= n; i++){int t = v[i - 1] + v[i - 2];v.push_back(t);}return v[n];
}
2. 尾递归可用迭代
- 尾递归函数是以递归调用作为结尾的函数,它是单向递归的特例,它的递归调用语句只有一个,而且放在过程最后。当递归调用返回时,返回到上一层递归调用语句的下一语句的时候,而这个位置正好是程序的结尾。
- 尾递归示意图:
-
举例:欧几里德求最大公约数
- 是用较大的数除以较小的数,较小的除数和得出的余数构成新的一对数,继续做上面的除法,直到出现能够整除的两个数。
- 递归求解最大公约数:
int gcd(int a, int b)
{if (b == 0)return a;elsegcd(b, a % b);
}- 迭代求解最大公约数:
int gcd(int a, int b)
{int tmp;//保存a%bwhile (b!=0){tmp = a % b;a = b;b = tmp;}return a;
}3. 借助栈实现非递归
1. 举例:二叉树的先序遍历
- 递归先序遍历:
void PreOrder(BTree T)//先序遍历
{if (T != NULL){cout << T->data << " ";//访问根结点PreOrder(T->lchild);//先序遍历左子树PreOrder(T->rchild);//先序遍历右子树}
}- 用栈先序遍历:
bool First(BTree T)
{stack<BTNode*>s;BTNode* p = T;if (p != NULL )//二叉树不为空{s.push(p);while (!s.empty())//栈不为空{p = s.top();cout << s.top()->data << " ";//先访问栈顶元素s.pop();//栈顶元素退栈if (p->lchild != NULL)s.push(p->rchild);//栈顶元素的右孩子结点进栈if (p->rchild != NULL)s.push(p->lchild);//栈顶元素的左孩子结点进栈}}return true;
}2. 举例:二叉树的中序遍历
- 递归中序遍历:
void InOrder(BTree T)//中序遍历
{if (T != NULL){InOrder(T->lchild);cout << T->data << " ";InOrder(T->rchild);}
}- 用栈中序遍历:
bool InOder(BTree T)
{stack<BTNode*>s;BTNode* p = T;while (p != NULL || !s.empty()){while (p != NULL)//当前结点不为空{s.push(p);p = p->lchild;}if (!s.empty()){cout << s.top()->data << " ";//访问栈顶元素p = s.top()->rchild;//先将栈顶元素的右孩子存储起来s.pop();//栈顶元素出栈}}return true;
}三、分治解题步骤
1. 分解:将要解决的问题分解为若干个规模较小、相互独立、与原问题形式相同的子问题
2. 治理:求解各个子问题。由于各个子问题与原问题形式相同,只是规模较小而已,而当子问题划分得足够小时,就可以用较简单的方法解决
3. 合并:按原问题的要求,将子问题的解逐层合并构成原问题的解
- 解决方案示意图:

四、汉诺塔问题
1. 问题
- 在经典汉诺塔问题中,有 3 根柱子及 N 个不同大小的穿孔圆盘,盘子可以滑入任意一根柱子。一开始,所有盘子自上而下按升序依次套在第一根柱子上(即每一个盘子只能放在更大的盘子上面)。移动圆盘时受到以下限制:
- 每次只能移动一个盘子;
- 盘子只能从柱子顶端滑出移到下一根柱子;
- 盘子只能叠在比它大的盘子上。
- 将所有盘子从第一根柱子移到最后一根柱子
2. 解题思路
- 当n=1(盘子数目为1)的时候,只需将盘子从A移到C即可
- 当n>1(盘子数目大于1)的时候,利用B作为辅助,将n-1个较小的盘子从A移到B,再将剩余的一个盘子从A移动到C。最后再将n-1个小盘从B依次移动到C。
3. 两个盘子演示

4. 三个盘子演示

5. 四个盘子演示

6. 代码
#include<iostream>
using namespace std;
void Move(int n, char x, char y)
{cout << "将编号为" << n << "的盘子从" << x << "移向" << y << endl;
}
void hanota(int n,char a,char b,char c)
{if (n == 1)Move(1, a, c);else{hanota(n - 1, a, c, b);//将n-1个盘子从a移到bMove(n, a, c);//将剩下的第n个盘子直接移到c处hanota(n - 1, b, a, c);//又将n-1个盘子从b移到c}
}
int main()
{hanota(3, 'A', 'B', 'C');return 0;
}