前言

最近在忙读研和课内项目的东西，因此有一个月没有更新博客了。之前学习的pyqt和ros的学习都落下了（还没开始）。这一个月大部分时间是在完成课内的自动控制创新实践项目，这个项目是我自己入坑的，希望把自己学的不怎么样的电机和以后可能从事的机器人学都巩固一下。

1. PMSM部分

三相永磁同步电机（PMSM）是我课上没学过的，我参考一些资料，貌似很多工业机器人都用它做伺服控制¹，因此我就打算学习一下PMSM的控制仿真。

1.1 数学模型

PMSM模型借用一下matlab官方文档对PMSM描述的图²：

电压方程：

$$\left[\begin{array}{c}{u}_a\\ u_b\\ u_c\end{array}\right]=\left[\begin{array}{ccc}{R}_s& 0& 0\\ 0& R_s& 0\\ 0& 0& R_s\end{array}\right]\left[\begin{array}{c}{i}_a\\ i_b\\ i_c\end{array}\right]+\left[\begin{array}{c}\frac{d{\psi }_a}{dt}\\ \frac{d{\psi }_b}{dt}\\ \frac{d{\psi }_c}{dt}\end{array}\right]$$

$R_s$ 为定子每相电阻，${\psi }_a$ 为a相磁链

磁链方程：

$$\left[\begin{array}{c}{\psi }_a\\ {\psi }_b\\ {\psi }_c\end{array}\right]=\left[\begin{array}{ccc}L& -M& -M\\ -M& L& -M\\ -M& -M& L\end{array}\right]\left[\begin{array}{c}{i}_a\\ i_b\\ i_c\end{array}\right]+\left[\begin{array}{c}{\psi }_{fa}\\ {\psi }_{fb}\\ {\psi }_{fc}\end{array}\right]$$

• ${\psi }_{fa}$ 为a相绕组和永磁体交链的磁链，与转子空间位置有关
• PMSM气隙均匀分布，因此各相自感和互感为常数

$$\left[\begin{array}{c}{\psi }_{fa}\\ {\psi }_{fb}\\ {\psi }_{fc}\end{array}\right]={\psi }_m\left[\begin{array}{c}cos({\theta }_e)\\ cos({\theta }_e-2\pi /3)\\ cos(\theta +2\pi /3)\end{array}\right]$$

一般定子绕组为Y型接法，中性点无接线引出，则有三相电流之和为零，磁链方程化简为：

$$\left[\begin{array}{c}{\psi }_a\\ {\psi }_b\\ {\psi }_c\end{array}\right]=(L+M)\left[\begin{array}{c}{i}_a\\ i_b\\ i_c\end{array}\right]+{\psi }_m\left[\begin{array}{c}cos({\theta }_e)\\ cos({\theta }_e-2\pi /3)\\ cos(\theta +2\pi /3)\end{array}\right]$$

将PMSM的abc相模型转化为按转子定向的dq模型，变换矩阵P为：

$$\left[\begin{array}{c}d\\ q\\ \ast \end{array}\right]=P\left[\begin{array}{c}a\\ b\\ c\end{array}\right]=2/3\ast \left[\begin{array}{ccc}cos({\theta }_e)& cos({\theta }_e-2\pi /3)& cos(\theta +2\pi /3)\\ -sin({\theta }_e)& -sin({\theta }_e-2\pi /3)& -sin({\theta }_e+2\pi /3)\\ 1/2& 1/2& 1/2\end{array}\right]$$

其中，abc可代表电压、电流和磁链，dq同理

逆变换为：

$$P^{-1}=\left[\begin{array}{ccc}cos({\theta }_e)& -sin({\theta }_e)& 1\\ cos({\theta }_e-2\pi /3)& -sin({\theta }_e-2\pi /3)& 1\\ cos({\theta }_e+2\pi /3)& -sin({\theta }_e+2\pi /3)& 1\end{array}\right]$$

代入电压方程：

$$P^{-1}\left[\begin{array}{c}{u}_d\\ u_q\\ \ast \end{array}\right]=R_s{P}^{-1}\left[\begin{array}{c}{i}_d\\ i_q\\ \ast \end{array}\right]+p(P^{-1}\left[\begin{array}{c}{\psi }_d\\ {\psi }_q\\ \ast \end{array}\right])$$

$p(\cdot )$为微分算子

整理得：
$$\begin{array}{rl}\left[\begin{array}{c}{u}_d\\ u_q\\ \ast \end{array}\right]& =R_s\left[\begin{array}{c}{i}_d\\ i_q\\ \ast \end{array}\right]+Pp(P^{-1})\left[\begin{array}{c}{\psi }_d\\ {\psi }_q\\ \ast \end{array}\right]+\left[\begin{array}{c}\frac{d{\psi }_d}{dt}\\ \frac{d{\psi }_q}{dt}\\ \ast \end{array}\right]\\ & =R_s\left[\begin{array}{c}{i}_d\\ i_q\\ \ast \end{array}\right]+{\omega }_e\left[\begin{array}{c}-{\psi }_q\\ {\psi }_d\\ \ast \end{array}\right]+\left[\begin{array}{c}\frac{d{\psi }_d}{dt}\\ \frac{d{\psi }_q}{dt}\\ \ast \end{array}\right]\end{array}$$

带入磁链方程：

$$\begin{array}{r}{P}^{-1}\left[\begin{array}{c}{\psi }_d\\ {\psi }_q\\ \ast \end{array}\right]=(L+M)P^{-1}\left[\begin{array}{c}{i}_d\\ i_q\\ \ast \end{array}\right]+{\psi }_m\left[\begin{array}{c}cos({\theta }_e)\\ cos({\theta }_e-2\pi /3)\\ cos(\theta +2\pi /3)\end{array}\right]\end{array}$$

整理得：

$$\begin{array}{rl}\left[\begin{array}{c}{\psi }_d\\ {\psi }_q\\ \ast \end{array}\right]& =(L+M)\left[\begin{array}{c}{i}_d\\ i_q\\ \ast \end{array}\right]+\left[\begin{array}{c}{\psi }_m\\ 0\\ 0\end{array}\right]\end{array}$$

求导得：
$$\begin{array}{rl}\left[\begin{array}{c}\frac{d{\psi }_d}{dt}\\ \frac{d{\psi }_q}{dt}\\ \ast \end{array}\right]& =(L+M)\left[\begin{array}{c}\frac{d{i}_d}{dt}\\ \frac{d{i}_q}{dt}\\ \ast \end{array}\right]\end{array}$$

带入电压方程得到最终数学模型：

$$\begin{array}{rl}\left[\begin{array}{c}{u}_d\\ u_q\end{array}\right]& =R_s\left[\begin{array}{c}{i}_d\\ i_q\end{array}\right]+\left[\begin{array}{c}-{\omega }_e{L}_q{i}_q\\ {\omega }_e(L_d{i}_d+{\psi }_m)\end{array}\right]+\left[\begin{array}{c}{L}_d\frac{d{i}_d}{dt}\\ L_q\frac{d{i}_q}{dt}\end{array}\right]\end{array}$$

此时，$L_d=L_q=L+M$

1.2 控制方法

在这里选用id=0的矢量控制方法，并对电流环使用前馈解耦³。控制框图如下：

1.3 PI参数整定

下面按工程设计方法整定PI参数⁴。

1.3.1 电流环

回看数学模型：

$$\begin{array}{rl}\left[\begin{array}{c}{u}_d\\ u_q\end{array}\right]& =R_s\left[\begin{array}{c}{i}_d\\ i_q\end{array}\right]+\left[\begin{array}{c}-{\omega }_e{L}_q{i}_q\\ {\omega }_e(L_d{i}_d+{\psi }_m)\end{array}\right]+\left[\begin{array}{c}{L}_d\frac{d{i}_d}{dt}\\ L_q\frac{d{i}_q}{dt}\end{array}\right]\end{array}$$

可以发现，dq轴控制电压具有耦合项，控制q轴电流会影响d轴电压，控制d轴电流影响q轴电压。因此在控制框图一节中，增加了前馈补偿部分：

这样使得dq轴电流的控制实现解耦，此时考虑如下电压方程：

$$\begin{array}{rl}\left[\begin{array}{c}{u}_d\\ u_q\end{array}\right]& =R_s\left[\begin{array}{c}{i}_d\\ i_q\end{array}\right]+\left[\begin{array}{c}{L}_d\frac{d{i}_d}{dt}\\ L_q\frac{d{i}_q}{dt}\end{array}\right]\end{array}$$

拉氏变换得传递函数：

$$\frac{U_d(s)}{I_d(s)}=\frac{1}{L_{d}s+R_s}$$

可得电流环动态框图⁵：

据博主所说，Kpwm取1即可，$T_d=T_s$。

按典1型系统设计，对象为：
$$\begin{array}{rl}G(s)& =\frac{1}{0.5T_{s}s+1}\ast \frac{1}{T_{d}s+1}\ast \frac{1}{T_{i}s+1}\ast \frac{1/R_s}{\frac{L_d}{R_s}s+1}\\ & \approx \frac{1/R_s}{(T_{\Sigma i}s+1)(\frac{L_d}{R_s}s+1)}\end{array}$$

小时间常数群直接等价于一个惯性环节

拟设计的典1型系统开环传递函数为：
$$G_{opi}(s)=\frac{K_c}{s(T_{c}s+1)}$$

由此可得：
$$\begin{gathered} {\tau }_i=L_d/R_s \\ {T}_c=T_{\Sigma i}=1.5T_s+T_i \end{gathered}$$

取工程最佳参数：
$$\xi =0.707K_c{T}_c=0.5$$

得到：

$$k_i=\frac{0.5R_s{\tau }_i}{T_c}$$

1.3.2转速环

电流环部分等效传递函数为：
$$\begin{array}{rl}{G}_i(s)& =\frac{G_{opi}(s)}{1+G_{opi}(s)}\\ & =\frac{1}{\frac{T_c}{K_c}{s}^2+\frac{1}{K_c}s+1}\\ & \approx \frac{1}{\frac{1}{K_c}s+1}\end{array}$$

忽略高阶部分

按照典2型系统设计转速环，框图为：

按典2型系统设计，对象为：
$$\begin{array}{rl}G(s)& =\frac{1}{T_{w}s+1}\ast \frac{\frac{3}{2}N{\psi }_m}{\frac{1}{K_c}s+1}\ast \frac{30/\pi }{Js}\\ & \approx \frac{1.5\ast 30N{\psi }_m/\pi }{Js(T_{\Sigma n}s+1)}\end{array}$$

拟设计的典2型系统开环传递函数为：
$$G_{opi}(s)=\frac{K_n({\tau }_{n}s+1)}{s^2(T_{n}s+1)}$$

由此可得：
$$T_n=T_{\Sigma n}=1/K_c+T_w$$

取工程最佳参数：
$$h=5$$

得到：

$$\begin{gathered} {\tau }_n=h{T}_n \\ {K}_n=\frac{h+1}{2h^2{T}_n^2} \end{gathered}$$

可以确定PI参数：

$$k_n=J{K}_n{\tau }_n/(1.5N{\psi }_m\ast 30/\pi )$$

1.4 仿真

电机参数如下，此参数参考了伺服电机，但有微小改动：

para	value
最大电流（A）	6.9
转子惯量 （kg*m2）	1e-4
dq轴电感 （mH）	8.35
极对数	4
定子电阻（Ω）	0.18
额定转速（rpm）	3000
磁链（Wb）	0.10667
减速箱减速比	10
PWM频率（Hz）	5000
电流滤波时间常数（ms）	1
转速滤波时间常数（ms）	1

1.4.1 电流环参数仿真

为了使电流环不受转速的影响，给负载输入端施加很大的反抗性负载，使电机堵转。

simulink仿真图：

给定q轴电流为3A，0.05s阶跃：

电流波形

转矩波形

1.4.2 转速环参数仿真

simulink仿真图：

• 0.02s给1000r/min 阶跃信号（空载）

转速波形：

力矩波形：

三相电压：

三相电流：

• 带动2N*m恒转矩负载，0.02s启动（1000rpm阶跃），0.1s调速至500rpm，0.25s反转（-500rpm），0.35s停转。

转速波形：

力矩波形：

三相控制电压：

2. 机械臂部分

机械臂选取puma560的前三个关节进行分析、控制和仿真。机械臂示意图（含其坐标系和各连杆质心）

机械臂参数⁶ 部分参考了论文和根据机械臂的sw模型⁷做了轻微修改。

机械臂参数：

Para	value
$h$ (m)	0.6718
$m_1$ (kg)	10
$m_2$ (kg)	17.4
$m_3$ (kg)	4.8
$I_1$ (kg*m2)	$diag([0.05,0.05,0.35])$
$I_2$ (kg*m2)	$diag([0.13,0.524,0.539])$
$I_3$ (kg*m2)	$diag([66e-3,12.5e-3,86e-3)$
$e_x$ (m)	0.361
$\vec{p}$ (m)	$[0.4318,-0.0203,-0.0453]$
$p_{12}$ (m)	-0.192
$p_{2c}$ (m)	0.025
$p_{3c}$ (m)	0.05

2.1 运动学

符号约定：
三个关节偏转角度分别设为${\theta }_1,{\theta }_2,{\theta }_3$
$h$ 为第一个关节与基座的距离
末端执行器坐标为$\vec{d}=(x_d,y_d,z_d{)}^T$
关节1到关节2距离为：$p_{12}$
关节3到末端执行器距离为：$e_x$
关节2到关节三平移向量为：$\vec{p}=(p_x,p_y,p_z{)}^T$

2.1.1 正运动学

从基座到关节1坐标系：先沿z轴平移h，然后旋转${\theta }_1$
$$T_1^0=\left[\begin{array}{cccc}{c}_1& -s_1& 0& 0\\ s_1& c_1& 0& 0\\ 0& 0& 1& h\\ 0& 0& 0& 1\end{array}\right]$$

关节1坐标系绕x轴旋转90°同时沿原来的y轴平移p12，然后才绕z旋转转一个${\theta }_2$

$$T_2^1=\left[\begin{array}{cccc}{c}_2& -s_2& 0& 0\\ 0& 0& -1& p_{12}\\ s_2& c_2& 0& 0\\ 0& 0& 0& 1\end{array}\right]$$

关节2坐标系先绕x转90°同时平移一个p向量 再绕z旋转${\theta }_3$

$$T_3^2=\left[\begin{array}{cccc}-s_3& -c_3& 0& p_x\\ c_3& -s_3& 0& p_y\\ 0& 0& 1& p_z\\ 0& 0& 0& 1\end{array}\right]$$

第三个关节到执行手腕沿x轴平移$e_x$

$$\left[\begin{array}{c}{x}_d\\ y_d\\ z_d\\ 1\end{array}\right]=T_1^0\ast T_2^1\ast T_3^2\ast \left[\begin{array}{c}{e}_x\\ 0\\ 0\\ 1\end{array}\right]$$

得到正运动学方程：

$x_d=p_x{c}_1{c}_2-p_y{c}_1{s}_2+p_z{s}_1-p_{12}{s}_1-e_x{c}_1{s}_{23}\cdot \cdot \cdot \cdot \cdot \cdot (1)$
$y_d=p_x{s}_1{c}_2-p_y{s}_1{s}_2-p_z{c}_1+p_{12}{c}_1-e_x{s}_1{s}_{23}\cdot \cdot \cdot \cdot \cdot \cdot (2)$

$z_d^{\prime }=z_d-h=p_x{s}_2+p_y{c}_2+e_x{c}_{23}\cdot \cdot \cdot \cdot \cdot \cdot (3)$

2.1.2 逆运动学

三式平方相加 $(1{)}^2+(2{)}^2+(3{)}^2$：
$$x_d^2+y_d^2+z_d^{\prime 2}={\vec{p}}^T\vec{p}+p_{12}^2+e_x^2-2p_{12}{p}_z-2e_x(p_x{s}_3-p_y{c}_3)$$

可解出第三个关节角${\theta }_3$ ：
$$sin({\theta }_3-{\alpha }_3)=\frac{\vec{p}{\vec{p}}^T+p_{12}^2+e_x^2-2p_{12}{p}_z-(x_d^2+y_d^2+z_d^{\prime 2})}{2e_x\sqrt{p_x^2+p_y^2}}=k_3$$

$$\begin{gathered} tan{\alpha }_3=\frac{p_y}{p_x} \\ {\theta }_3={\alpha }_3+asin(k_3) \\ {\theta }_3={\alpha }_3+\pi -asin(k_3) \end{gathered}$$

---

进而通过式(3)解出${\theta }_2$：
$$sin({\theta }_2+{\alpha }_2)=\frac{z_d^{\prime }}{\sqrt{x_d^2+y_d^2+z_d^{\prime 2}-(p_{12}-p_z{)}^2}}=k_2$$

$$\begin{gathered} tan{\alpha }_2=\frac{p_y+e_x{c}_3}{p_x-e_x{s}_3} \\ {\theta }_2=asin(k_2)-{\alpha }_2 \\ {\theta }_2=\pi -asin(k_2)-{\alpha }_2 \end{gathered}$$

---

最后通过式(1),(2)解出${\theta }_1$：
$$\begin{gathered} x_d=(p_x{c}_2-p_y{s}_2-e_x{s}_{23})c_1+(p_z-p_{12})s_1=k{x}_1{c}_1+k{x}_2{s}_1 \\ {y}_d=(p_{12}-p_z)c_1+(p_x{c}_2-p_y{s}_2-e_x{s}_{23})s_1=k{y}_1{c}_1+k{y}_2{s}_1 \end{gathered}$$

$${\theta }_1=atan(\frac{y_{d}k{x}_1-x_{d}k{y}_1}{x_{d}k{y}_2-y_{d}k{x}_2})$$

---

解的存在性：必须满足以下条件，才有解！！

$A=\vec{p}{\vec{p}}^T+p_{12}^2+e_x^2-2p_{12}{p}_z$
$B=2e_x\sqrt{p_x^2+p_y^2}$
$C=x_d^2+y_d^2+z_d^{\prime 2}$

1. $B-A\le C\le B+A$
2. $x_d^2+y_d^2\ge (p_{12}-p_z{)}^2$

解的个数

${\theta }_3$两个解，${\theta }_2$两个解，${\theta }_1$一个解，一共2x2x1=4个解

2.2 动力学

符号约定：
各关节转动惯量：$I_i=diag([I_{xi},I_{yi},I_{zi}])i=1,2,3$
各关节质量：$m_1,m_2,m_3$
关节到质心的距离：$p_{ic}i=2,3$

使用牛顿——欧拉迭代法求解其动力学方程⁸：

初始条件：
$$\begin{gathered} v_0=[0,0,0{]}^T \\ {\omega }_0=[0,0,0{]}^T \\ \dot{v_0}=[0,0,g{]}^T \\ \dot{{\omega }_0}=[0,0,0{]}^T \end{gathered}$$
前向迭代：
$$\begin{gathered} {\omega }_{i+1,i+1}=R_{i+1,i}{\omega }_{i,i}+{\dot{\theta }}_{i+1}{\hat{Z}}_{i+1} \\ {\dot{\omega }}_{i+1,i+1}=R_{i+1,i}{\dot{\omega }}_{i,i}+R_{i+1,i}{\omega }_{i,i}\times {\dot{\theta }}_{i+1}{\hat{Z}}_{i+1}+{\ddot{\theta }}_{i+1}{\hat{Z}}_{i+1} \\ {v}_{i+1,i+1}=R_{i+1,i}(v_{i,i}+{\omega }_{i,i}\times p_{i,i+1}) \\ {\dot{v}}_{i+1,i+1}=R_{i+1,i}({\dot{v}}_{i,i}+{\dot{\omega }}_{i,i}\times p_{i,i+1}+{\omega }_{i,i}\times ({\omega }_{i,i}\times p_{i,i+1})) \\ i=0,1,2 \end{gathered}$$

${\omega }_{i+1,i+1}$ 表示i+1坐标系的相对于世界坐标系的角速度在i+1坐标系下的表示
$R_{i+1,i}$ 表示从i+1坐标系旋转到i坐标系的旋转矩阵
$p_{i,i+1}$ 表示从i关节到i+1关节的距离向量

计算各连杆质心速度、加速度、角速度和角加速度：

$$\begin{gathered} {\omega }_{c,i}={\omega }_{i,i} \\ {\dot{\omega }}_{c,i}={\dot{\omega }}_{i,i} \\ {v}_{c,i}=v_{i,i}+{\omega }_{i,i}\times p_{i,c} \\ {\dot{v}}_{c,i}={\dot{v}}_{i,i}+{\dot{\omega }}_{i,i}\times p_{i,c}+{\omega }_{i,i}\times ({\omega }_{i,i}\times p_{i,c}) \\ i=1,2,3 \end{gathered}$$

由此可计算出各关节受合力和合力矩：
$$\begin{gathered} F_i=m_i{\dot{v}}_{c,i} \\ {N}_i=I_i{\dot{w}}_{c,i}+w_{c,i}\times I_i{w}_{c,i} \end{gathered}$$

反向迭代初始条件：

$$\begin{gathered} f_4=[0,0,0{]}^T \\ {n}_4=[0,0,0{]}^T \end{gathered}$$

反向迭代：
$$\begin{gathered} f_{i,i}=R_{i,i+1}{f}_{i+1,i+1}+F_i \\ {n}_{i,i}=R_{i,i+1}{n}_{i+1,i+1}+p_{i,c}\times F_i+p_{i,i+1}\times R_{i,i+1}{f}_{i+1,i+1}+N_i \\ i=1,2,3 \end{gathered}$$

最终各关节力矩为：
$${\tau }_i=n_{i,i}{\hat{Z}}_{i}i=1,2,3$$

2.3 轨迹规划

轨迹规划部分我们使用三次样条曲线（三次样条曲线规划原理参考博客⁹），首先在笛卡尔空间规划圆弧轨迹，然后使用逆运动学反推关节空间轨迹，然后对关节空间应用三次样条曲线规划得到各时刻的角度、角速度和角加速度。

选取初始机械臂三关节角度为：$[0,0,-\pi /5]$
拟规划轨迹函数表达式：
$$\begin{array}{rl}x& =0.644\\ y& =0.3cos(t)-0.1527\\ z& =0.3sin(t)+0.6436\\ t& \in [0,2\pi ]\end{array}$$

拟跟踪圆弧轨迹：

在关节空间规划使用了博主⁹ 提到的指定初始速度v0和最终速度vn时的参数计算方法，先计算出中间点速度，然后再使用已知始末两点位置速度，推算该小段的三次方程系数。

我们把圆弧轨迹分为30个点，则有30段路程，假设启动和停止这两段花费0.4s，其余的花费0.2s，则这个任务需要在6.4s内完成。

三个关节的期望角度、角速度和角加速度为：

---

---

2.4 控制方法

对puma560的前三个关节（三自由度）进行圆弧轨迹跟踪。由于puma560前三个关节是实现位置调整，后三个关节是实现姿态调整，对于圆弧轨迹跟踪来说，只需要研究前三个关节的运动，这有利于对问题的简化又不失一般性。机构和期望轨迹如下图：

其中，红色球形标记为机械臂末端执行器位置，绿色圆弧为机械臂期望跟踪的轨迹。

2.4.1 基于模型的重力补偿PD控制⁸

对于我们讨论的三自由度机械臂模型，关节角向量为：$\Theta =({\theta }_1,{\theta }_2,{\theta }_3)$，则动力学模型的一般式如下：
$$\tau =M(\Theta )\ddot{\Theta }+V(\Theta ,\dot{\Theta })+G(\Theta )$$
其中，$\tau$为力矩向量，$M(\Theta )$为质量矩阵，$V(\Theta ,\dot{\Theta })$为复杂的非线性耦合项，$G(\Theta )$为关节受到重力矩阵。

对于复杂的非线性时变项由关节角度和其一阶导数的相乘或平方项构成，考虑这一项需要耗费大量的计算资源，而且已有证明指出，仅考虑重力补偿的PD控制器已经可以达到系统的全局渐进稳定⁸。
忽略非线性项后动力学模型为：
$$\tau \approx M(\Theta )\ddot{\Theta }+G(\Theta )$$
进而设计重力补偿的控制率：
$$\begin{gathered} \tau =M(\Theta )f+G(\Theta ) \\ f={\ddot{\Theta }}_d+K_d({\dot{\Theta }}_d-\dot{\Theta })+K_p({\Theta }_d-\Theta ) \end{gathered}$$
联立上面三式得到系统模型为：
$$\ddot{e}+K_d\dot{e}+K_{p}e=0$$
其中，$e={\Theta }_d-\Theta$。这时希望系统具有临界阻尼的特性，因此希望参数具有关系：
$$K_d=2\sqrt{K_p}$$

由此得到控制框图如下：

---

• 仿真结果

任意指定一组PD参数：P = 5，D = 0.1进行10s仿真，对关节角度跟随效果如下：

由图可见，关节角度跟踪快速而且较为准确，其中前两个关节跟踪误差小，而第三个关节跟踪误差较大，这是因为在轨迹规划的时候，第三个关节要活动的范围更大，因此会出现明显偏差。但对于较为随意指定的PD参数，机械臂跟踪效果良好，体现了这种控制方法的鲁棒性。
现在，我们尝试按照使系统具有临界阻尼特性的规则进行参数设置，若使系统具有较大带宽，不妨取${\omega }_n=5rad/s$。此时P = 25, D = 10。仿真得到关节角度跟随效果如下：

可见效果明显提升，三个关节期望角度和实际角度基本吻合。我们进一步量化这两组参数的差距，我们定义当前时刻的误差等于末端执行器在笛卡尔坐标系下位置与期望位置的欧氏距离，我们对这两组PD参数进行量化评估：

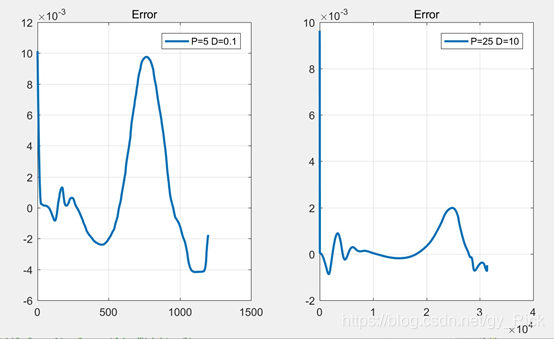
由图可见，使用后一组PD参数下，末端执行器的跟踪误差比第一组显著减小，误差小于大部分时刻在1mm以内。

2.4.2 非线性前馈控制⁸

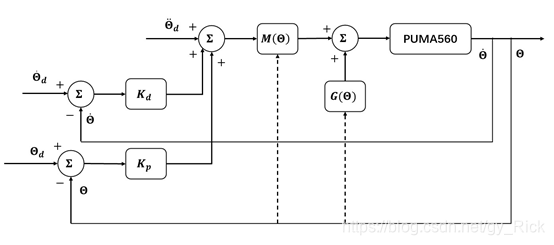
非线性前馈控制将充分利用机械臂的动力学模型，将期望轨迹对应的期望关节角度、角速度和角加速度通过正运动学计算出期望的力矩，将此力矩作为前馈量和PID控制器输出的控制量相加作为总控制量对机械臂进行控制，控制框图如下：

---

• 仿真结果

对这种控制方式沿用上一节的PD参数进行仿真，得到关节角度跟踪效果如下：

由上图可见，采用非线性前馈PD控制三组关节跟踪与期望角度基本吻合。这得益于非线性前馈完全使用了机械臂的动力学模型，而且前馈控制的好处是可以离线计算前馈的力矩，这有利于快速伺服。
再次评估在同组PD参数下第一种控制方案和改组方案的误差对比：

两种方案在轨迹跟踪误差上都小于2mm，但第一种方法在精度上比第二种方法略胜一筹。

3. 集成仿真

在设计过程中，小组成员分成PMSM和机械臂两部分进行设计。机械臂部分，由以上控制方法得知，输入控制量是力矩给定值，也就是说，对应的电机的输出需要跟踪给定力矩。考虑到此情况，我们仅需使用PMSM的电流环部分即可，因为力矩和电流有明确的关系，因此只需要给出期望力矩的对应电流给定，即可使电机输出期望力矩。
另外，仅存在电流环的PMSM会受到电压限制而造成失步，因此对于输入到电机的负载也需要准确计算。实际应用中，电机通过减速箱驱动真实负载运作，但仿真环境下难以得到两种机构拖动的模拟，只能在仿真时准确计算机械臂相应位姿的负载，用这个数值输入到PMSM模型。而电机的转动除以减速比后，必须等于关节转动角度。
若当前时刻对应的关节角度、角速度和角加速度分别为${\Theta }_t,{\dot{\Theta }}_t,{\ddot{\Theta }}_t$，这时候对应动力学模型为：
$${\tau }_t=M({\Theta }_t)\ddot{\Theta }+V({\Theta }_t,{\dot{\Theta }}_t)+G({\Theta }_t)$$
对比电机运动方程：
$$T_e-T_L=Jd\omega /dt$$
可以发现当前时刻下机械臂关节负载为：
$$T_L=V({\Theta }_t,{\dot{\Theta }}_t)+G({\Theta }_t)$$

---

• 仿真结果：

总体集成仿真图如下：

由于所有部件仿真所需时间很长，限于硬件限制，在这里仅对第三个关节使用PMSM驱动，而前两个关节依然使用直接给理想力矩源的方式，通过对第三个关节的控制即可验证模型的可用性。控制方案选择非线性前馈的方式，PD参数选择同第二部分。

关节跟踪图：

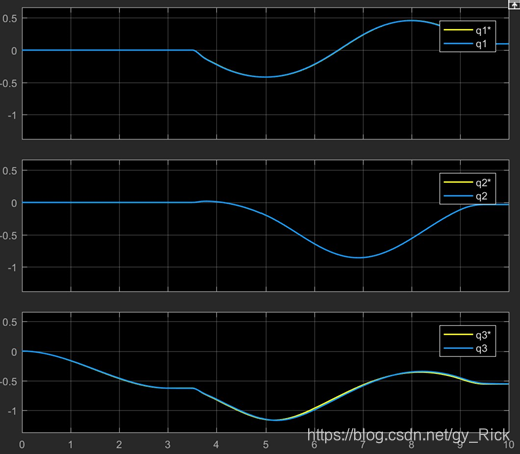
PMSM提供的力矩跟随期望力矩图：

使用PMSM和未使用时的误差对比图：

最后：

还参考了很多其他资料，感谢这些作者^{10 11 12}

相关代码：github

引用

---

1. 黄志坚.机器人驱动与控制及应用实例[M].化学工业出版社:北京,2016. ↩︎

2. https://www.mathworks.com/help/physmod/sps/ref/pmsm.html?s_tid=srchtitle ↩︎

3. 袁雷,胡冰新,魏克银,等.现代永磁同步电机控制原理及MATLAB仿真[M].北京航空航天大学出版社:北京,2016. ↩︎

4. 阮毅,杨影,陈伯时.电力拖动自动控制系统——运动控制系统[M].机械工业出版社:北京,2016. ↩︎

5. sy243772901.永磁同步电机矢量控制（三）——电流环转速环 PI 参数整定[EB/OL].https://blog.csdn.net/sy243772901/article/details/82221672,2019-05-17. ↩︎

6. Armstrong B, Khatib O, Burdick J. The explicit dynamic model and inertial parameters of the PUMA
   560 arm[C]//Robotics and Automation. Proceedings. 1986 IEEE International Conference on. IEEE, 1986,
   3: 510-518. ↩︎

7. https://github.com/nimasarli/puma560_description ↩︎

8. John J.Craig.机器人学导论[M].机械工业出版社:中国北京,2006:60-65, 235-237, 243-244. ↩︎ ↩︎ ↩︎ ↩︎

9. xuuyann.机器人轨迹规划：三次样条曲线[EB/OL].https://blog.csdn.net/qq_26565435/article/details/105940288,2020-05-05. ↩︎ ↩︎

10. ZHENG Fan. ENGG 5402 Course Project: Simulation of PUMA 560 Manipulator[D] ,2015-04-05. ↩︎

11. 付博.永磁同步电动机动态解耦控制技术研究[D].黑龙江:哈尔滨工业大学,2010-06. ↩︎

12. 潘月斗.现代交流电机控制技术[M].机械工业出版社:北京,2018 ↩︎