题目链接:https://leetcode.cn/problems/xuan-zhuan-shu-zu-de-zui-xiao-shu-zi-lcof/
1. 题目介绍(11. 旋转数组的最小数字)
把一个数组最开始的若干个元素搬到数组的末尾,我们称之为数组的旋转。
给你一个可能存在 重复 元素值的数组 numbers ,它原来是一个升序排列的数组,并按上述情形进行了一次旋转。请返回旋转数组的最小元素。例如,数组 [3,4,5,1,2] 为 [1,2,3,4,5] 的一次旋转,该数组的最小值为 1。
注意,数组 [a[0], a[1], a[2], …, a[n-1]] 旋转一次 的结果为数组 [a[n-1], a[0], a[1], a[2], …, a[n-2]] 。
【测试用例】:
示例 1:
输入:numbers = [3,4,5,1,2]
输出:1
示例 2:
输入:numbers = [2,2,2,0,1]
输出:0
【条件约束】:
提示:
- n == numbers.length
- 1 <= n <= 5000
- -5000 <= numbers[i] <= 5000
- numbers 原来是一个升序排序的数组,并进行了 1 至 n 次旋转
【相同题目】:
注意:本题与 154. 寻找旋转排序数组中的最小值II 相同
2. 题解
2.1 穷举起手 – O(n)
时间复杂度O(n),空间复杂度O(1)
人狠话不多,起手就穷举,简单又易懂,大力有奇效。
class Solution {// 第一种方法:穷举public int minArray(int[] numbers) {int min = numbers[0];for (int i = 1; i < numbers.length; i++){if (numbers[i] <= min){min = numbers[i];}}return min;}
}
2.2 二分法 – O(logn)
时间复杂度O(logn),空间复杂度O(1)
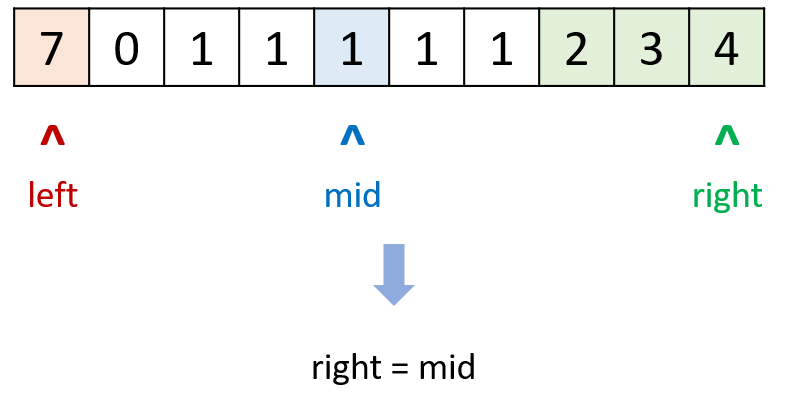
二分清晰但略微麻烦,定义头尾索引,循环缩进,不断缩小范围,逼近最小值,但存在两个特例:
- 数组本身,即把一个数组的前0个元素搬到数组的末尾,如 [1,2,3,4,5];
nums[start] = nums[mid] = nums[end],如出现[1,0,1,1,1]时,找不到最小值0,而是会返回1,因此当该情况方式时,我们将采用顺序遍历的方式,在start到end比较找出最小值。
class Solution {// 第二种方法:二分法public int minArray(int[] numbers) {// 1. 判空if (numbers == null || numbers.length <= 0) return -1;// 2. 初始化头索引、尾索引、中值索引int start = 0;int end = numbers.length-1;// 3. 初始化mid为start,是为了防止出现未旋转的特例,即把一个数组的前0个元素搬到数组的末尾(数组本身)int mid = start;// 4. 循环结束条件:start指到了最小值的前一个元素,end指到了最小值while (numbers[start] >= numbers[end]){if (end - start == 1) {mid = end;break;}// 5. 计算中点mid = (start + end)/2;// 7. 特例:当出现[1,0,1,1,1],这种start=mid=end的情况,就无法正确判断最小值了,所以这里我们让它去顺序遍历,找出最小值if (numbers[start] == numbers[mid] && numbers[end] == numbers[mid]) return minForAll(numbers,start,end);// 6. 与中点比较,不断缩小范围if (numbers[start] <= numbers[mid]){start = mid;} else if (numbers[end] >= numbers[mid]){end = mid;}}return numbers[mid];}// 顺序遍历,找出start到end范围内的最小值public int minForAll(int[] numbers,int start, int end){int min = numbers[start];for (int i = start; i <= end; i++){if (numbers[i] <= min){min = numbers[i];}}return min;}
}
二分改进:
- 时间复杂度O(logn),在特例情况下(例如 [1,1,1,1])会退化到O(n)
- 空间复杂度O(1)

class Solution {public int minArray(int[] numbers) {int i = 0, j = numbers.length - 1;while (i < j) {int m = (i + j) / 2;if (numbers[m] > numbers[j]) i = m + 1;else if (numbers[m] < numbers[j]) j = m;else {int x = i;for(int k = i + 1; k < j; k++) {if(numbers[k] < numbers[x]) x = k;}return numbers[x];}}return numbers[i];}
}
2.3 库函数求解 – O (n*log (n))
时间复杂度O (n*log (n)),空间复杂度O(1)
除此之外,还可以采用Stream,以及Collection求解最大/最小值
class Solution {// 第三种方法:库函数public int findMin(int[] numbers) {Arrays.sort(numbers);return numbers[0];}
}
3. 参考资料
[1] 面试题11. 旋转数组的最小数字(二分法,清晰图解)-- 图片来源 & 二分改进来源
[2] 【算法基础】Java如何使用库函数得出一个数组的最大/最小值?