DiffRate详解:高效Vision Transformers的可微压缩率
- 0. 引言
- 1. 相关内容介绍
- 1.1 Transformer Block
- 1.2 令牌修剪和合并
- 1.3 修剪和合并的统一
- 2 DiffRate中的创新点
- 2.1 令牌排序
- 2.2 压缩率重参数化
- 2.3 训练目标
- 3. 算法流程
- 4. 总结
0. 引言
就当前的Vision Transformers(例如vit)而言,模型是大规模的。有学者提出使用令牌压缩的方法,即通过修剪(删除)或合并令牌来加速模型训练。尽管最近的先进方法取得了巨大的成功,但是仍需要对令牌的压缩比进行手动设置且数值是固定的。从压缩率出发,作者提出了DiffRate的概念。整篇文章的创新点分为三个部分:
压缩比是可训练的。DiffRate可以将损失函数的梯度传播到压缩比上,压缩比在以前的工作中被认为是一个不可微的超参数。在这种情况下,不同的层可以自动学习不同的压缩率,而不需要额外的开销。修剪和合并令牌可以同时进行。而在以往的作品中,它们是相互隔离的。DiffRate达到了SOTA。大量的实验表明,DiffRate达到了最先进的性能。例如,通过将学习到的分层压缩率应用于现有的ViT-H (MAE)模型,实现了40%的FLOPs减少和1.5倍的吞吐量提高,在没有微调的情况下,在ImageNet上的精度下降了0.16%,甚至优于以前的方法。
论文名称:DiffRate : Differentiable Compression Rate for Efficient Vision Transformers
论文地址:https://arxiv.org/abs/2305.17997
代码地址:https://github.com/opengvlab/diffrate
1. 相关内容介绍
首先,为了方便大家理解。先介绍相关内容。
1.1 Transformer Block
在 Vit 的Transformer Block中,输入数据经过 Attention 块后经过线性层得到对应的输出 (注意:Transformer Block 不包含Embedded Patches 部分)。整体网络结构如下所示。

假设第 l 个Transformer Block的输入token为 X l ∈ R N × D X^l\in R^{N\times D} Xl∈RN×D,其中 N N N 表示 token 的长度; D D D 表示 token 的维度。则变压器块的前向传播表示为:
X ^ l = X l + A t t e n t i o n ( X l ) X l + 1 = X ^ l + M L P ( X ^ l ) \hat X^l = X^l + Attention(X^l) \\\ X^{l+1} = \hat X^l +MLP( \hat X^l) X^l=Xl+Attention(Xl) Xl+1=X^l+MLP(X^l)
其中, l ∈ L l∈L l∈L, L L L 为网络深度。其中, A t t e n t i o n Attention Attention 和 M L P MLP MLP 分别表示变压器块中的自注意模块和MLP模块; X ^ l \hat X^l X^l 为注意力模块的输出 token。
1.2 令牌修剪和合并

如图2所示,现有的 Token 压缩方法通常位于 Transformer Block中的 Attention模块后,即对 X ^ l \hat X^l X^l 进行修剪或合并操作。
X ^ p l ← f p ( X ^ l , α p l ) X ^ m l ← f m ( X ^ l , α m l ) \hat X^l_p \leftarrow f_p(\hat X^l, \alpha^l_p) \\\ \hat X^l_m \leftarrow f_m(\hat X^l, \alpha^l_m) \\\ X^pl←fp(X^l,αpl) X^ml←fm(X^l,αml) 其中, f p , f m f_p,f_m fp,fm 分别表示修剪和合并操作; α p l , α m l \alpha^l_p, \alpha^l_m αpl,αml 分别表示对应操作的压缩率; X ^ p l ∈ R N p l × D , X ^ m l ∈ R N m l × D \hat X^l_p \in R^{N^l_p \times D}, \hat X^l_m \in R^{N^l_m \times D} X^pl∈RNpl×D,X^ml∈RNml×D 分别表示对应操作的输出,然后被输入到 Transformer Block中的 MLP 模块中。因此,每个块的剪枝压缩率和合并压缩率分别定义为 α p l = ( N − N p l ) / N \alpha^l_p = (N−N^l_p)/N αpl=(N−Npl)/N 和 α m l = ( N − N m l ) / N \alpha^l_m = (N−N^l_m)/N αml=(N−Nml)/N 。
现有的方法取得了巨大的成功。如:EViT 保留了重要的令牌,同时在重要性指标的指导下融合了注意力和MLP之间的不重要令牌(Token 合并)。ToMe 在前景和背景中合并了类似的Xl标记(Token 合并)。注意:DynamicViT 在MLP之后修剪令牌,实验结果发现它在注意之后也能很好地工作。然而,它们仍需要谨慎使用手工制作压缩率块,这是繁琐的,并导致次优性能,如下图所示。

1.3 修剪和合并的统一
DiffRate 实现了令牌修剪和合并的统一,通过最优搜索选择最佳的压缩率。给定一个 pre-trained 模型 W ∗ W^* W∗,令牌压缩的目的是最小化训练集上的分类损失 L c l s L_{cls} Lcls 在目标FLOPs T内。这个问题可以总结为一个优化问题,用公式表示为:
α p ∗ , α m ∗ = a r g m i n α p , α m L c l s ( W ∗ ( X ) , Y ∣ α p , α m ) s . t . F ( α p , α m ) ≤ T , 0 ≤ α p l , α m l ≤ 1 X ^ l = f c ( X ^ l , α p l , α m l ) , l ∈ [ L ] \alpha^*_p,\alpha^*_m = argmin_{\alpha_p, \alpha_m} L_{cls}(W^*(X),Y|\alpha_p, \alpha_m) \\\ s.t. F(\alpha_p, \alpha_m) \leq T, 0 \leq \alpha^l_p, \alpha^l_m \leq 1 \\\ \hat X^l = f_c(\hat X^l, \alpha^l_p, \alpha^l_m) ,l\in [L] αp∗,αm∗=argminαp,αmLcls(W∗(X),Y∣αp,αm) s.t.F(αp,αm)≤T,0≤αpl,αml≤1 X^l=fc(X^l,αpl,αml),l∈[L] 其中, α p = { α p l } l = 1 L \alpha_p = \{\alpha^l_p \}^L_{l=1} αp={αpl}l=1L 和 α m = { α m l } l = 1 L \alpha_m = \{\alpha^l_m \}^L_{l=1} αm={αml}l=1L 分别表示所有块的修剪和合并的压缩率。 F ( α p , α m ) F(\alpha_p , \alpha_m) F(αp,αm) 表示相应的FLOPs,可以表示为压缩率的一种可微方式。最后,通过 DiffRate 中微分学习得到 α p ∗ , α m ∗ \alpha^*_p,\alpha^*_m αp∗,αm∗。
通过统一的令牌压缩公式,DiffRate 有足够的能力表达各种压缩方法。当 f c = f p , α m l = 0 f_c = f_p, α^l_m = 0 fc=fp,αml=0 时,DiffRate 表示令牌剪枝,剪枝压缩率 α p l α^l_p αpl 可微。当 f c = f m , α p l = 0 f_c = f_m, α^l_p = 0 fc=fm,αpl=0时,DiffRate变为可微令牌合并。在这项工作中,设置 f c = f m ◦ f p f_c = f_m◦f_p fc=fm◦fp,这意味着先修剪令牌,然后合并令牌。在这种情况下,DiffRate通过可微分压缩率无缝集成令牌修剪和令牌合并。
问题:然而,求解上述等式中的优化问题具有一定的挑战性。上述优化目标的等式与基于梯度的方法的压缩率是不可微的。像通道修剪那样直接学习0-1的token掩码是不可行的,因为每个图像可能会丢失不同数量的token。这使得很难并行化计算。例如,DynamicViT 和SPViT 为每个输入图像维护一个掩码向量,但它们仍然需要手动设计压缩率,以确保所有图像保留相同数量的令牌。下一节将介绍一种用于压缩率可微搜索的新技术。
2 DiffRate中的创新点
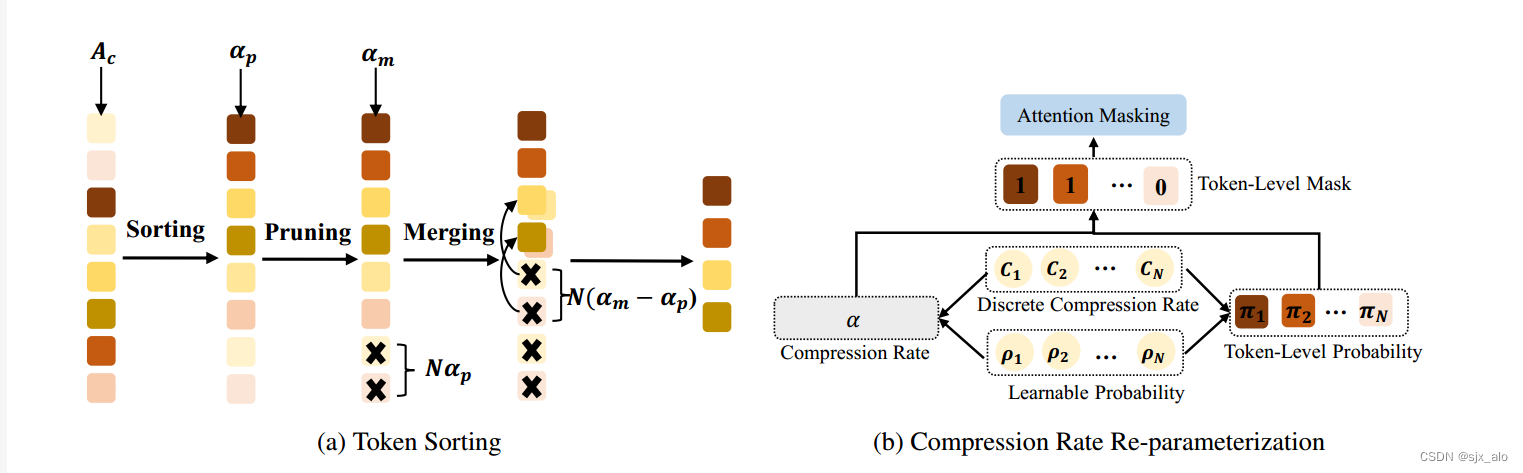
在 DiffRate 中,引入了一种称为可微分离散代理(DDP)的新方法,它包括两个关键组件:一个标记排序过程,用标记重要性度量来识别重要标记,一个重新参数化技巧,通过梯度反向传播来优化选择top-K重要标记。DDP的整体流水线如下图所示。
2.1 令牌排序
在 DiffRate 中,为了找到 top-K 重要性令牌,作者通过令牌重要性度量对令牌进行排序。在这里,作者使用了同EViT的重要度测量 class attention A c ∈ R 1 × N A_c∈R^{1×N} Ac∈R1×N 。 class attention 和 image tokes 之间的关系可以用下列式子表示:
A c = S o f t m a x ( q c K T / D ) , a n d X c = A c V , A_c = Softmax(q_cK^T/\sqrt{D}), and X_c = A_cV, Ac=Softmax(qcKT/D),andXc=AcV,其中, q c ∈ R 1 × D K ∈ R N × D V ∈ R N × D 和 X c ∈ R 1 × D q_c∈R^{1×D} K∈R^{N×D} V∈R^{N×D} 和 X_c∈R^{1×D} qc∈R1×DK∈RN×DV∈RN×D和Xc∈R1×D 分别表示类令牌、键矩阵、值矩阵、自关注层类令牌的查询向量。class attention A c A_c Ac 衡量每个图像令牌对类令牌的贡献。关注度越高,对应的图像标记对最终输出的影响越显著,意味着其重要性越大。
如上图(a)所示,在第1个变压器块中修剪 N α p Nα_p Nαp 个不重要的符号。之后,使用余弦相似性来度量 N ( α m − α p ) N(α_m - α_p) N(αm−αp) 个不重要标记与其余标记之间的相似性。对于相似的令牌对,通过直接平均它们来生成一个新的令牌。通过上述排序-修剪-合并管道,在DiffRate 中以可学习的压缩率最优地确定每个块中需要修剪和合并的令牌数量。
因此,DiffRate可以无缝地集成令牌修剪和合并。
2.2 压缩率重参数化
DDP使用重参数化技巧使剪枝和合并压缩率可微。通过使用单个变量α来表示两种压缩率来简化符号。
离散速率的再参数化。从本质上讲,使压缩率可微就是确定在保证最优性的情况下应该丢弃多少令牌。
为了解决这个问题,作者将压缩率重新参数化为多个候选压缩率的可学习组合。具体来说,作者引入一个离散的压缩率集,表示为C = {C1, C2,…, CN},其中Ck = k−1 N表示应该删除的最重要的(k−1)个标记。通过将可学习概率ρk分配给每个候选压缩率Ck,使k=1 ρk =1,压缩率可以写成
α = ∑ k = 1 N C k ρ k ( 7 ) α = \sum^{N}_{k=1}C_kρ_k \ \ \ \ \ \ \ \ (7) α=k=1∑NCkρk (7)
通过使用离散的各个候选压缩率的集合,将学习压缩率的优化问题可以转化为概率ρk的学习问题。
如上图 (b) 所示,在 C k C_k Ck和 ρ k ρ_k ρk下,第 k k k个重要令牌被压缩的概率可计算为
π 1 = 0 , π k = ρ N + 2 − k + ⋅ ⋅ ⋅ + ρ N − 1 + ρ N , k ≥ 2 ( 8 ) π_1 = 0, π_k = ρ_{N+2 - k} +···+ ρ_{N−1} + ρ_N, k≥2 \ \ \ \ \ \ \ \ (8) π1=0,πk=ρN+2−k+⋅⋅⋅+ρN−1+ρN,k≥2 (8)其中 π 1 = 0 π_1 = 0 π1=0 表示最重要的令牌始终被保留。容易看出 π k ≤ π k + 1 π_k≤π_{k+1} πk≤πk+1。因此,带有 DDP的 DiffRate 符合这样一个事实,即不太重要的令牌应该具有更大的压缩概率。为了使训练和推理一致,将 π k π_k πk 转换为0-1掩码,公式为:
m k = { 0 , π k ≥ α , 1 , π k < α , ( 9 ) m_k =\begin{cases} 0,π_k≥α,\\ 1,π_k < α,\end{cases} \ \ \ \ \ \ \ \ (9) mk={0,πk≥α,1,πk<α, (9)其中, m k = 1 m_k = 1 mk=1 表示保留第 k k k 个令牌,反之亦然。
在每个视觉转换块中,通过实例化了两个独立的重参数化模块来学习剪枝和合并压缩率。因此,它生成两个令牌级掩码,即修剪掩码和合并掩码,每个令牌分别表示 m k p m^p_k mkp 和 m k m m^m_k mkm。注意,在上一个块中删除的令牌也必须在这个块中压缩。因此,最终的掩码定义为
m k = m k ⋅ m k p ⋅ m k m , ( 10 ) m_k = m_k·m^p_k·m^m_k, \ \ \ \ \ \ \ \ (10) mk=mk⋅mkp⋅mkm, (10)其中右边的 m k m_k mk 是最后一个块中第 k k k 个令牌的掩码。
为了保持梯度反向传播链,作者在公式(10)中使用掩码 m k m_k mk 将令牌下降转换为注意掩蔽。继 DynamicViT 之后。为了实现这一点,作者构建了一个与每个自操作操作的注意图具有相同维度的注意掩码:
M i , j = { 1 , i = j , m j , i = j ( 11 ) M_{i,j} =\begin{cases} 1,i = j, \\ m_j, i = j \end{cases} \ \ \ \ \ \ \ \ (11) Mi,j={1,i=j,mj,i=j (11)注意掩码防止所有压缩令牌和其他令牌之间的交互,除了它自己。然后作者使用这个掩码修改下一个自关注模块中的Softmax操作:
S = Q K T D , S ^ i , j = e x p ( S i , j ) M i , j ∑ k = 1 N e x p ( S i , k ) M i , k ( 12 ) S =\frac{QK^T}{\sqrt D}, \\ \hat S_{i,j} = \frac {exp(S_{i,j})M_{i,j}}{ \sum^N_{k=1} exp(S_{i,k})M_{i,k}} \ \ \ \ \ \ \ \ (12) S=DQKT,S^i,j=∑k=1Nexp(Si,k)Mi,kexp(Si,j)Mi,j (12)其中, Q ∈ R N × D Q∈R^{N×D} Q∈RN×D 是查询矩阵, S ∈ R N × N S∈R^{N×N} S∈RN×N 是Softmax之前的原始注意映射,而 S ^ i , j \hat S_{i,j} S^i,j 实际上是用来更新令牌的。等式(11-12)使得损失函数的梯度传播到 mask m上。
2.3 训练目标
通过最小化总损耗解决了上文所述的优化问题:
L = L c l s + λ f L f ( α p , α m ) , ( 13 ) L = L_{cls} + λ_fL_f (α_p, α_m), \ \ \ \ \ \ \ \ (13) L=Lcls+λfLf(αp,αm), (13)其中, L f = ( F ( α p , α m ) − T ) 2 L_f = (F(α_p, α_m)−T)^2 Lf=(F(αp,αm)−T)2 是约束FLOPs的损耗。超参数 λ f λ_f λf 平衡了两个损耗项,在实验中将其默认设置为5。
在网络反向传播过程中,作者利用直通估计器(straight-through-estimator, STE)来计算等式(11)的梯度。因此,可以使用链式法则来计算 L L L 相对于 ρ k ρ_k ρk 的梯度:
∂ L ∂ ρ k = ∑ j = 1 N ∂ L ∂ m j ∂ m j ∂ π j ∂ π j ∂ ρ k ≈ ∑ j = 1 N ∂ L ∂ m j ∂ π j ∂ ρ k ( 14 ) \frac{∂_L}{∂_{ρ_k}} =\sum^N_{j=1} \frac{∂_L}{∂_{m_j}} \frac{∂_{m_j}}{∂_{π_j}} \frac{∂_{π_j}}{∂_{ρ_k}} ≈ \sum^N_{j=1} \frac {∂_L}{∂_{m_j}} \frac{∂_{π_j}}{∂_{ρ_k}} \ \ \ \ \ \ \ \ (14) ∂ρk∂L=j=1∑N∂mj∂L∂πj∂mj∂ρk∂πj≈j=1∑N∂mj∂L∂ρk∂πj (14)由于 ρ k ρ_k ρk可通过等式(14)微分,压缩率 α α α 可以用梯度反向传播方程 (7) 进行优化。
3. 算法流程

算法1给出了 DiffRate 的整体训练算法。它包括三个步骤:带 ρ k ρ_k ρk 的正向模型(第2-6行),计算优化目标(第7-9行),反向传播和 DDP 中的 ρ k ρ_k ρk 更新(第10-11行)。DiffRate算法通过将 ρ k ρ_k ρk 更新为可微的形式来找到最优压缩率,得到的压缩率可以直接应用于现成的模型。
4. 总结
实验结果表明,即使没有对模型进行微调,DiffRate也可以与以前最先进的令牌压缩方法相当或更好的方法想媲美。此外,DiffRate具有很高的数据效率,因为它仅使用1,000张图像就可以确定适当的压缩率。
总的来说,所提出的DiffRate框架通过揭示压缩率的重要性,为令牌压缩提供了一个新的视角。
如果有什么疑问欢迎在评论区提出,对于共性问题可能会后续添加到文章介绍中。