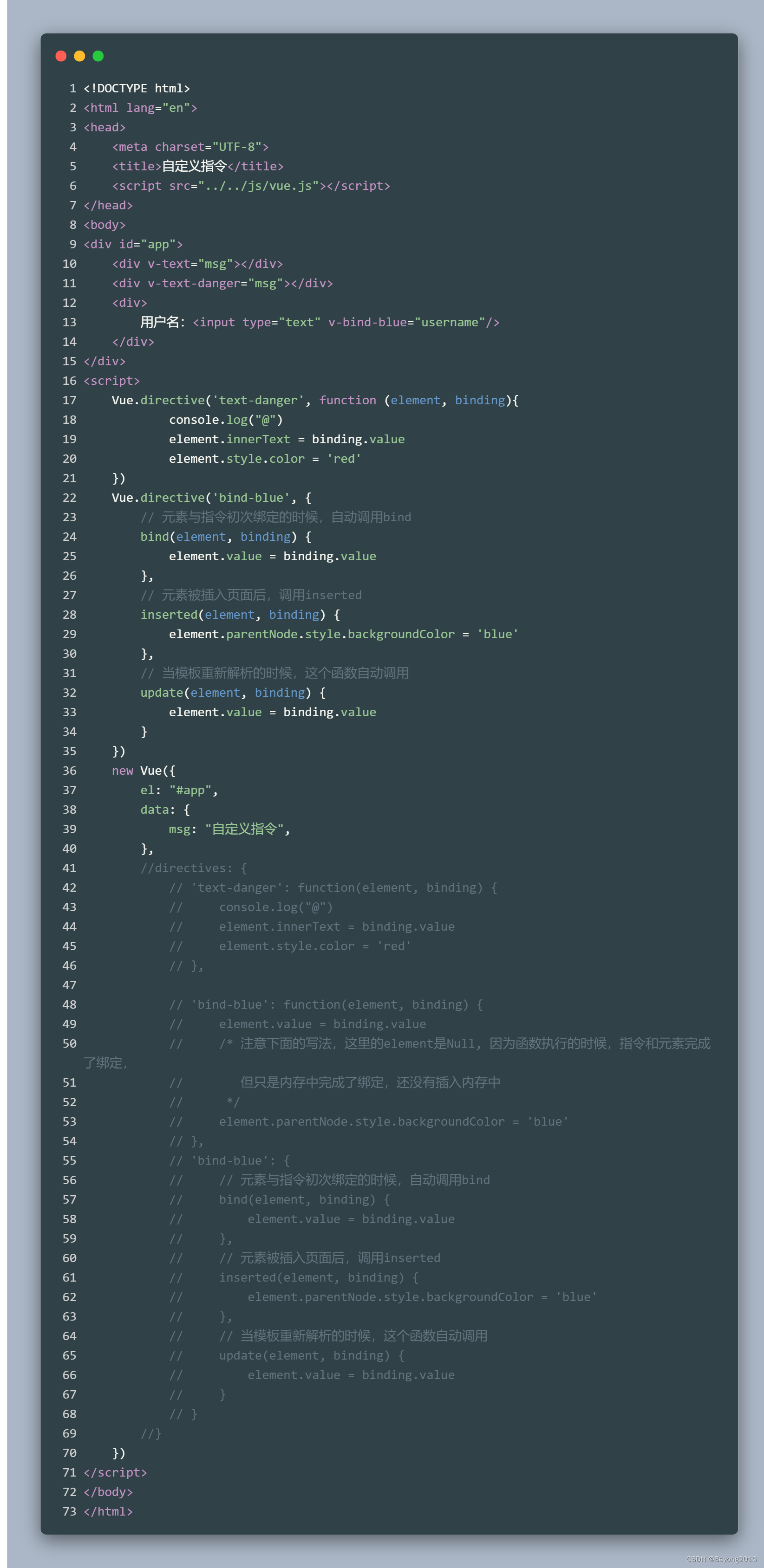
传统的交叉熵损失函数通常用于多分类问题,而在多标签分类问题中,每个样本可能属于多个标签,因此需要使用一些新的技术来优化交叉熵损失函数。
一种常用的技术是标签平滑(Label Smoothing),它可以优化传统的交叉熵损失函数,使其适用于多标签分类问题。标签平滑通过将真实标签的概率分布从原来的one-hot编码改为一个平滑的分布,从而减少模型在训练过程中的过拟合风险。
标签平滑的数学形式为:
y i ′ = ( 1 − ϵ ) y i + ϵ K y_i' = (1-\epsilon) y_i + \frac{\epsilon}{K} yi′=(1−ϵ)yi+Kϵ
其中, y i y_i yi是真实标签的one-hot编码形式, y i ′ y_i' yi′是平滑后的标签, ϵ \epsilon ϵ是平滑度, K K K是标签的数量。
在使用标签平滑时,交叉熵损失函数的数学形式变为:
L C E = − ∑ i = 1 N ∑ j = 1 K y i j ′ log p i j L_{CE}=-\sum_{i=1}^{N}\sum_{j=1}^{K}y_{ij}'\log{p_{ij}} LCE=−i=1∑Nj=1∑Kyij′logpij
其中, y i j ′ y_{ij}' yij′是第 i i i个样本的第 j j j个标签的平滑标签, p i j p_{ij} pij是模型对第 i i i个样本的第 j j j个标签的预测概率。
标签平滑的优点在于,它可以减少模型在训练过程中的过拟合风险,从而提高模型的泛化性能。同时,标签平滑还可以使得模型对不确定性的处理更加鲁棒,从而提高模型的鲁棒性。
需要注意的是,标签平滑的平滑度 ϵ \epsilon ϵ通常需要根据具体的任务和数据集来进行调整,以达到最佳的效果。过高或过低的平滑度可能会导致模型的性能下降。