hdu6350 /// tarjan+并查集+组合+最大流思想

题目大意：

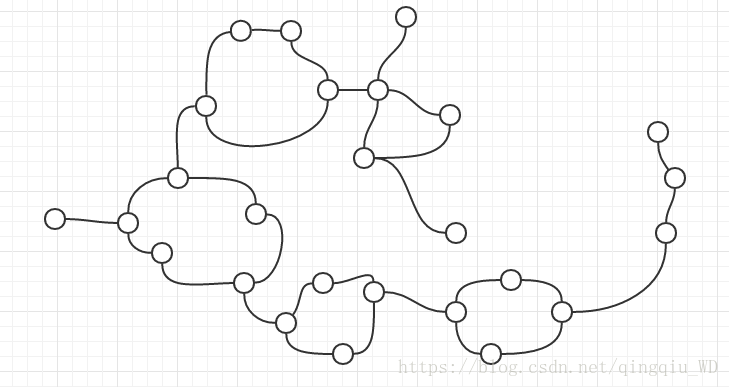
给定n个点 m条边没有重边的仙人掌图（没有一条边会同时存在与两个环 也就是环都是相互独立的）

求任意两点间 i^j^maxflow(i,j)的总和 maxflow为两点间最大流

 

题解：https://blog.csdn.net/du_lun/article/details/81610624

对于两点间的最大流

若是一个环上的两点 那么最大流就会等于两条路径上的最短边的总和

那么任意两点间的最大流 就是其余边加上最短边后去掉最短边 

这样这个图就变成了一棵树

此时按边长逆序排序 取出一条边求最大流 然后将两个分量合并成一个点

取出的边长就是两个联通分量间的最大流 因为每次取出的都是比之前取出的更小的边

求异或值不能n^2枚举两点 按数的32位枚举 

每次合并联通分量后 更新这个联通分量中每一个二进制位有多少0 1

当两个联通分量间的最大流

第 j 位为1时 那么使得该位异或后为1 两个联通分量的第j位应为 1 1 或 0 0

第 j 位为0时 那么使得该位异或后为1 两个联通分量的第j位应为 1 0 或 0 1

组合一下 方案数乘以 2^j 就是最大流第 j 位的贡献

 这题会爆long long 需要用unsigned long long 

#include <bits/stdc++.h>
using namespace std;
#define INF 0x3f3f3f3f
#define LLINF 0x3f3f3f3f3f3f3f3f
#define LL long long
#define mem(i,j) memset(i,j,sizeof(i))
const int N=1e5+5;struct EDGE {int u,v,nt; LL w;bool operator <(const EDGE& e)const {return w>e.w;}
}E[N<<2],e[N<<1],t[N<<1]; // 图的邻接表 树边集 暂存
int head[N], tot, cnt;
void addE(int u,int v,LL w) {E[tot].u=u, E[tot].v=v;E[tot].w=w, E[tot].nt=head[u];head[u]=tot++;
}int low[N], ind, dfn[N], fa[N];int pos[N]; // 记录走过的环上 i点对应的边在邻接表中的索引
void cir(int u,int v,int id) {int c=0, k=v;while(k!=u) {t[c++]=E[pos[k]], k=fa[k];} // t暂存环上的所有边t[c++]=E[id];LL mini=LLINF;for(int i=0;i<c;i++) // 找到最短边if(t[i].w<mini) mini=t[i].w, k=i;for(int i=0;i<c;i++) // 其他边加上最短边长 存入数边集if(i!=k) t[i].w+=mini, e[cnt++]=t[i];
}void tarjan(int u,int f) {dfn[u]=low[u]=++ind;fa[u]=f;for(int i=head[u];~i;i=E[i].nt) {int v=E[i].v;if(v==f) continue;if(!dfn[v]) {pos[v]=i, tarjan(v, u);low[u]=min(low[u],low[v]);} else low[u]=min(low[u],dfn[v]);}for(int i=head[u];~i;i=E[i].nt) {int v=E[i].v;if(low[v]>dfn[u]) e[cnt++]=E[i]; // 树边// v以及其子孙节点连的所有点中dfn最小的点比u还小// 说明u往下有一个环且v在环中 那么此时u到v的这条边为树边else if(dfn[v]>dfn[u] && fa[v]!=u) cir(u,v,i); // 环
    }
}int f[N];
int getf(int x) {if(f[x]==x) return x;else return f[x]=getf(f[x]);
}
int n, m;
LL c[N][35][2];
// c[i][j][0/1]是第i个联通分量二进制的第j位为0 1的数量
unsigned long long ans;
void init() {tot=cnt=ind=0; ans=0;for(int i=1;i<=n;i++) {head[i]=-1; f[i]=i;dfn[i]=0;for(int j=0;j<=30;j++)c[i][j][1]=(i>>j)&1, c[i][j][0]=((i>>j)&1)^1;}
}int main()
{int t; scanf("%d",&t);while(t--) {scanf("%d%d",&n,&m);init();while(m--) {int u,v; LL w; scanf("%d%d%lld",&u,&v,&w);addE(u,v,w); addE(v,u,w);}tarjan(1,-1);sort(e,e+cnt);for(int i=0;i<cnt;i++) {int fu=getf(e[i].u);int fv=getf(e[i].v);LL w=e[i].w;for(int j=0;j<=30;j++)if(w&(1LL<<j)) {ans+=c[fu][j][1]*c[fv][j][1]*(1LL<<j);ans+=c[fu][j][0]*c[fv][j][0]*(1LL<<j);} else {ans+=c[fu][j][0]*c[fv][j][1]*(1LL<<j);ans+=c[fu][j][1]*c[fv][j][0]*(1LL<<j);}f[fu]=fv;for(int j=0;j<=30;j++)c[fv][j][1]+=c[fu][j][1],c[fv][j][0]+=c[fu][j][0];}printf("%llu\n",ans);}return 0;
}