一条路径只是一个空间结构——空间中从初始位姿过渡到最终位姿的一个图形。而轨迹是具有特定时间属性的一条路径。例如,从 A A A 到 B B B 是路径,但如果规定了 10 10 10 秒的时间或 2 m ⋅ s − 1 2 m\cdot s^{-1} 2m⋅s−1 的速度,则变成从 A A A 到 B B B 的轨迹。轨迹的一个重要特征是要平滑——位置和姿态随时间流畅地变化。
平滑一维轨迹
我们从时间的标量函数开始讨论。这种函数的重要特征是它的初始值和最终值是确定的,而且函数是光滑的。所谓光滑是指它的低阶时间导数是连续的。通常速度和加速度都必须是连续的,有时加速度的导数或加加速度也需要连续。这种函数的一个常见代表是时间多项式函数。多项式函数容易计算,而且可以方便地提供所需的连续性和边界条件。比较常用的是五次多项式:
S ( t ) = A t 5 + B t 4 + C t 3 + D t 2 + E t + F S(t)=At^5+Bt^4+Ct^3+Dt^2+Et+F S(t)=At5+Bt4+Ct3+Dt2+Et+F其中时间 t ∈ [ 0 , T ] t\in [0,T] t∈[0,T]。其一阶和二阶导数也是光滑的多项式:
S ˙ ( t ) = 5 A t 4 + 4 B t 3 + 3 C t 2 + 2 D t + E S ¨ ( t ) = 20 A t 3 + 12 B t 2 + 6 C t + 2 D \begin{array}{c} \dot{S}(t)=5At^4+4Bt^3+3Ct^2+2Dt+E \\[1em] \ddot{S}(t)=20At^3+12Bt^2+6Ct+2D \end{array} S˙(t)=5At4+4Bt3+3Ct2+2Dt+ES¨(t)=20At3+12Bt2+6Ct+2D
轨迹上定义了位置、速度和加速度的边界条件,一般情况下速度和加速度的边界条件均为零。在 t = 0 t=0 t=0 和 t = T t=T t=T 时分别将边界条件代入上述方程,得到6个方程,我们可以写成如下的矩阵形式:
( s 0 s T s ˙ 0 s ˙ T s ¨ 0 s ¨ T ) = ( 0 T 5 0 5 T 4 0 20 T 3 0 T 4 0 4 T 3 0 12 T 2 0 T 3 0 3 T 2 0 6 T 0 T 2 0 2 T 2 2 0 T 1 1 0 0 1 1 0 0 0 0 ) ( A B C D E F ) \left( \begin{array}{c} s_0\\ s_T\\ \dot{s}_0\\ \dot{s}_T\\ \ddot{s}_0\\ \ddot{s}_T\\ \end{array} \right) =\left( \begin{array}{c} 0\\ T^5\\ 0\\ 5T^4\\ 0\\ 20T^3\\ \end{array}\begin{array}{c} 0\\ T^4\\ 0\\ 4T^3\\ 0\\ 12T^2\\ \end{array}\begin{array}{c} 0\\ T^3\\ 0\\ 3T^2\\ 0\\ 6T\\ \end{array}\begin{array}{c} 0\\ T^2\\ 0\\ 2T\\ 2\\ 2\\ \end{array}\begin{array}{c} 0\\ T\\ 1\\ 1\\ 0\\ 0\\ \end{array}\begin{array}{c} 1\\ 1\\ 0\\ 0\\ 0\\ 0\\ \end{array} \right) \left( \begin{array}{c} A\\ B\\ C\\ D\\ E\\ F\\ \end{array} \right) ⎝⎜⎜⎜⎜⎜⎜⎛s0sTs˙0s˙Ts¨0s¨T⎠⎟⎟⎟⎟⎟⎟⎞=⎝⎜⎜⎜⎜⎜⎜⎛0T505T4020T30T404T3012T20T303T206T0T202T220T1100110000⎠⎟⎟⎟⎟⎟⎟⎞⎝⎜⎜⎜⎜⎜⎜⎛ABCDEF⎠⎟⎟⎟⎟⎟⎟⎞
由于该矩阵是方阵,我们可以使用标准的线性代数方法来求解系数向量 ( A , B , C , D , E , F ) (A,B,C,D,E,F) (A,B,C,D,E,F),如MATLAB中的算子。五次多项式的加速度是一条光滑的三次曲线,加速度率是一个抛物线。机器人工具箱中的函数tpoly可以生成一个五次多项式轨迹,例如:
>> s = tpoly(0, 1, 50);
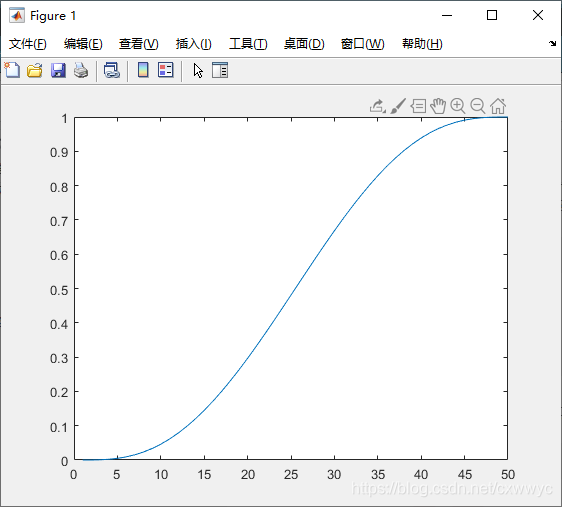
返回一个 50 × 1 50\times 1 50×1 的列向量,其值在 0 0 0 到 1 1 1 范围内分 50 50 50 个时间步平滑变化。我们可以绘制出该轨迹曲线:
>> plot(s)
相应的速度和加速度可以通过增加输出选项参数返回:
>> [s, sd, sdd] = tpoly(0, 1, 50);
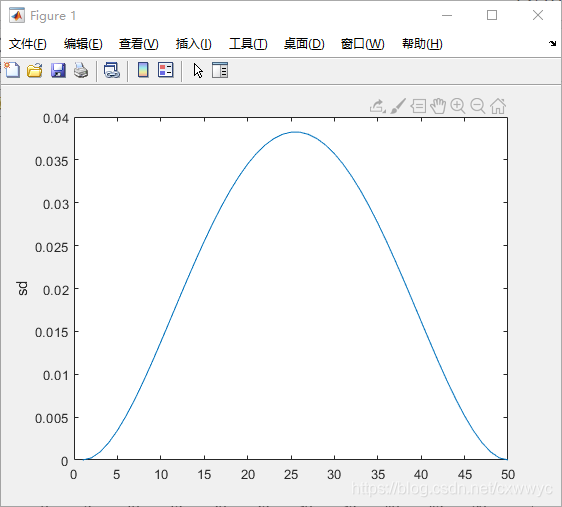
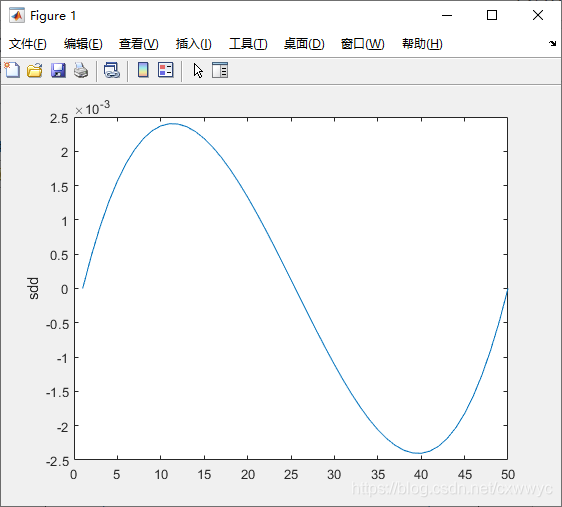
速度和加速度分别为sd和sdd。如图所示,可以看出初始和终点的速度和加速度都是零——函数默认值。
初始速度和终点速度也可以被设置为非零值:
>> s = tpoly(0, 1, 50, 0.5, 0);
在这种情况下,初始速度为 0.5 0.5 0.5 和最终速度为 0 0 0。如下图所示的结果也体现出多项式轨迹的一个问题。非零的初始速度导致多项式轨迹的中间值超过终点值——轨迹中的峰值达到5,超出0到1的范围。
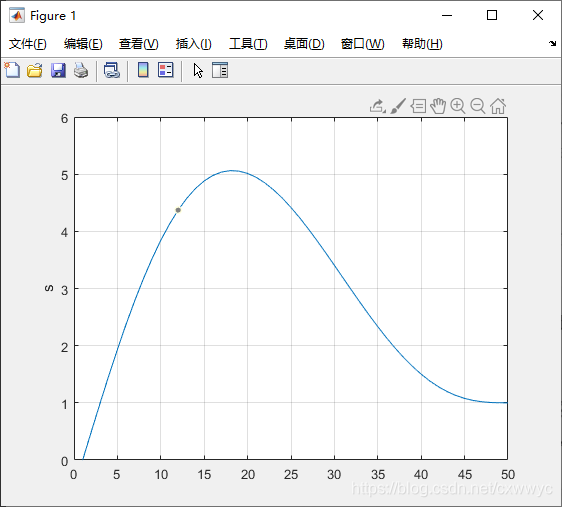
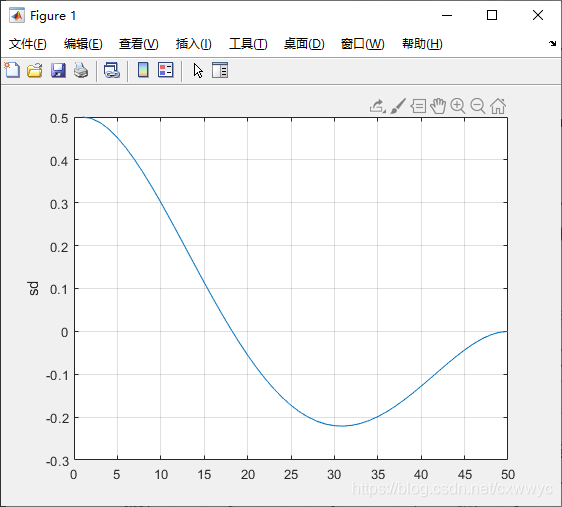
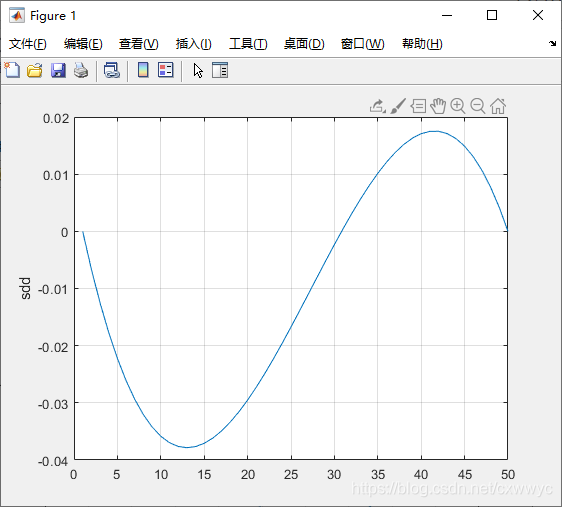
多项式轨迹另一个很实际的问题是它的速度,我们目光回到初速度为零的情况,可以从图中看出。其速度在 t = 25 t=25 t=25 时达到最大值,这意味着大多数时间的速度都远小于这个最大值。计算其平均速度为
>> mean(sd) / max(sd)
ans =0.5231
只有最大值的 52 % 52\% 52%。一个真正的机器人关节都有一个额定的最大速度,而且为了使关节运动时间最短,应使其运行在最大速度上的时间尽可能长。因此,我们希望速度曲线的顶部是一条平直线。一种公认的较理想的选择是采用混合曲线轨迹,即由中间的恒速段平直线加上两侧的加速段和减速段多项式曲线构成的轨迹。回到第一个例子,其混合轨迹是
>> [s, sd, sdd] = lspb(0, 1, 50);
其中的参数与tpoly中的含义相同,轨迹曲线如图所示。
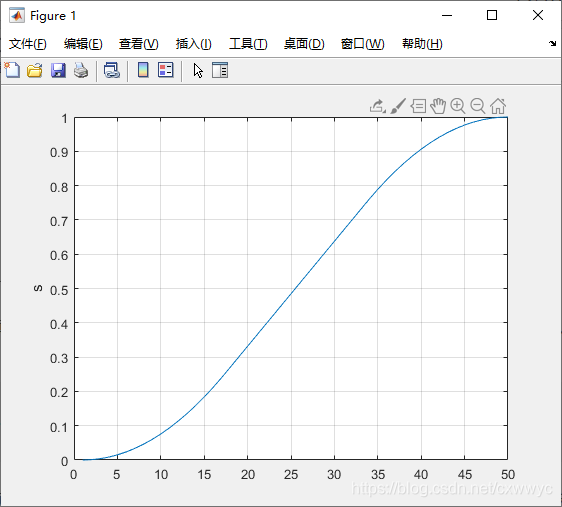
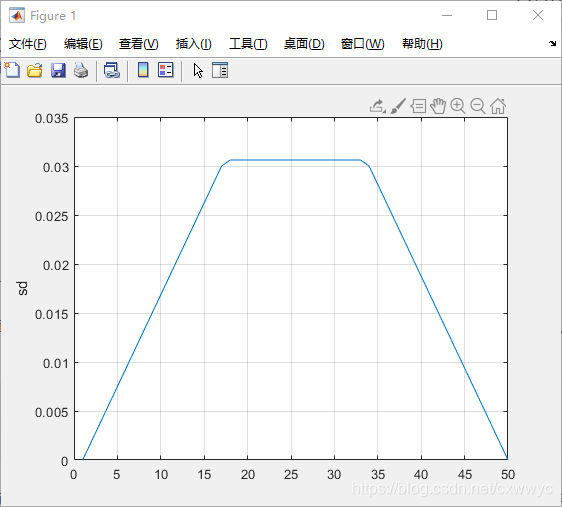
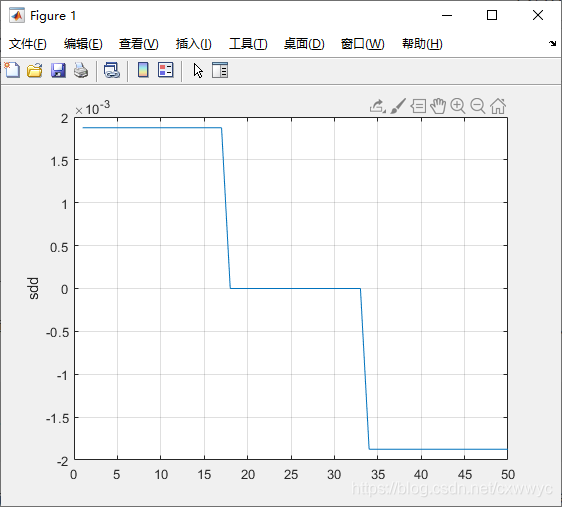
轨迹由一条线段(匀速)与两条抛物线混合而成,因此得名lspb。术语“混合”(blend)常用来指轨迹加入线性部分。这种类型的轨迹由于其速度-时间曲线的形状也被称作梯形轨迹,并普遍应用于工业马达驱动中,有时候移动机器人的速度规划也是梯形轨迹。
这里,函数lspb自己选择的直线段速度为
>> max(sd)
ans =0.0306
但也可以通过第四个输入参数为直线段指定一个速度:
>> s = lspb(0, 1, 50, 0.025);
>> s = lspb(0, 1, 50, 0.035);
如果将改变了直线速度后的结果绘图,可以发现,随着直线段速度的增大,该段占有的时间会减少,且最终会变为零。事实上,速度值是不能任意选择的,过高或过低的最大速度值都将产生一个不可行的轨迹,且函数返回错误。同时要指出,该系统是欠约束的,有5个约束条件(总时间,起点和终点的位置及速度),却有6个自由度(混合时间,3个抛物线系数和两个线性系数)。
多维轨迹
大多数实用的机器人都有一个以上的运动轴或自由度。我们将其用向量形式表示为 x ∈ R M x\in\mathbb{R}^M x∈RM,M代表自由度的数目。轮式移动机器人由它的位置 ( x , y ) (x, y) (x,y) 或位姿 ( x , y , 0 ) (x, y, 0) (x,y,0) 来描述,而关节臂式机器人的末端工具则有位置 ( x , y , z ) (x, y,z) (x,y,z),姿态 ( θ r , θ p , θ y ) (\theta_r,\theta_p,\theta_y) (θr,θp,θy),或位姿 ( x , y , z , θ r , θ p , θ y ) (x, y,z,\theta_r,\theta_p,\theta_y) (x,y,z,θr,θp,θy)。因此我们需要从初始位姿向量到最终位姿向量的多维平滑运动。
将平滑的标量轨迹扩展成向量情况是非常简单直接的,在工具箱中可以使用函数mtraj完成。例如,分 50 50 50 个时间步从 ( 0 , 2 ) (0, 2) (0,2) 移动到 ( 1 , − 1 ) (1, -1) (1,−1) 可以表示为
>> x = mtraj(@tpoly, [0, 2], [1, -1], 50);
>> x = mtraj(@lspb, [0, 2], [1, -1], 50);
可得一个 50 × 2 50\times2 50×2 的矩阵 x x x,其中每一行对应一个time step,每一列对应一个轴。输人给mtraj的第一个参数是一个函数,即tpoly或lspb,它生成一个标量轨迹。以lspb为例,绘制其轨迹为
>> plot(x)
如图所示
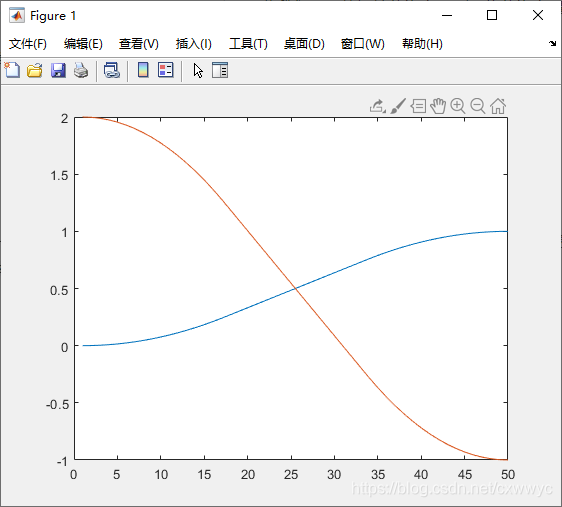
对于三维空间中的位姿问题,可以考虑先用以下方法将位姿齐次矩阵 T T T 转换为一个六维向量:
>> x = [transl(T); tr2rpy(T)']
然后再产生相应的轨迹。不过后面会看到,对于描述姿态的3个角度的插值会存在一定的限制。