目录
一、二分搜索树
1.1什么是二分搜索树
1.2创建一个二分搜索树
(1)二分搜索树的内部构建
(2)插入操作
(3)判断一个val值是否存在
(4)按照节点的深度先序遍历打印BST
(5)关于最小值
(6)关于最大值
(7)删除任意结点
HashMap底层基于哈希表(数组+链表)的实现。
TreeMap底层基于二分搜索平衡树的实现(BeeTree)。
一、二分搜索树
1.1什么是二分搜索树
右基础BST没有结构上的特点,他是一个二叉树,每个结点的值大于其左右左子树的结点值,小于其右子树的结点值,左子树<树根<右子树。
存储的元素必须具备可比较性。
(1)二分搜索树的中序遍历:能得到一个完全升序的数组(有序数组)
(2)在BST查找一个元素是否存在,其实就是一个二分查找,时间复杂度为O(logn)走到空树还没找到,说明该元素不存在。BST在实际的生产工作中有着广泛应用。
1.2创建一个二分搜索树
(1)二分搜索树的内部构建
和正常的二叉树是相通的,创建一个size来记录长度,root作为根节点。
然后TreeNode类中有val表示该节点的值,left表示左子树,right表示右子树。
public class MyBinarySearchTree {private int size;private TreeNode root;private static class TreeNode{int val;TreeNode left ;TreeNode right;public TreeNode(int val) {this.val = val;}}
}(2)插入操作
插入之后的新节点一定是叶子结点,不断比较当要插入的值和树根的大小关系,不断走左右子树,如果值比左子树小就走左子树,值比右子树大就走右子树。直到走到null,就构造新节点放入带插入元素的值。
public void add(int val){root = add(root,val);}private TreeNode add(TreeNode root, int val) {if(root==null){size++;return new TreeNode(val);}if(val>root.val){root.right = add(root.right,val);}if(val<root.val){root.left = add(root.left,val);}return root;}(3)判断一个val值是否存在
判断则创建一个递归,两个终止条件当走到最后root==null,则证明这个二叉搜索树中不包含该val值,则返回false。另一种是当root.val == val,则找到了这个该元素返回true即可。
然后如果值比左子树小就递归左子树,值比右子树大就递归右子树。
public Boolean contains(int val){return contains(root,val);}private Boolean contains(TreeNode root, int val) {if(root==null){return false;}if(root.val == val){return true;}if(val<root.val){return contains(root.left,val);}else{return contains(root.right,val);}} public static void main(String[] args) {MyBinarySearchTree bst = new MyBinarySearchTree();bst.add(41);bst.add(28);bst.add(58);bst.add(15);System.out.println(bst.contains(58));System.out.println(bst.contains(22));}
(4)按照节点的深度先序遍历打印BST
主要就是运用二叉树的先序遍历,然后再根据深度加上--。
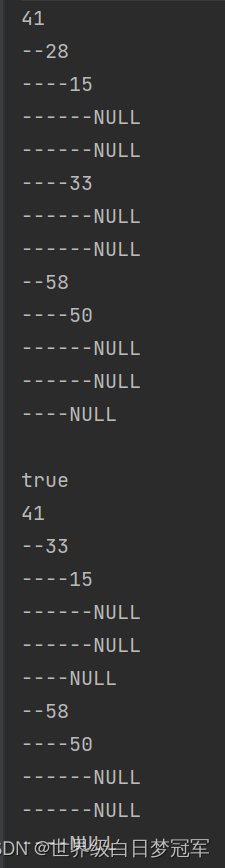
public String toString() {StringBuilder sb = new StringBuilder();generateBSTSting(root,0,sb);return sb.toString();}private void generateBSTSting(TreeNode root, int depth, StringBuilder sb) {if(root==null){sb.append(generateHeightString(depth)).append("NULL\n");return ;}sb.append(generateHeightString(depth)).append(root.val).append("\n");generateBSTSting(root.left,depth+1,sb);generateBSTSting(root.right,depth+1,sb);}private String generateHeightString(int depth){StringBuilder sb = new StringBuilder();for (int i = 0; i < depth; i++) {sb.append("--");}return sb.toString();} public static void main(String[] args) {MyBinarySearchTree bst = new MyBinarySearchTree();bst.add(41);bst.add(28);bst.add(58);bst.add(15);bst.add(33);bst.add(50);System.out.println(bst.toString());}
(5)关于最小值
最小值位于左子树的最左侧,一路向左走,碰到第一个root.left == null的结点,root即为最小值结点。输出最小值时直接返回该root即可。
如果是删除最小值,那么就需要创建一个TreeNode类型的right存储root.right然后将root.left = root = null,再将树的结点个数size--最后返回right。
public int min(){if (size == 0) {throw new NoSuchElementException("bst is empty!no min");}TreeNode min = findMinNode(root);return min.val;}public int removeMin(){if (size == 0) {throw new NoSuchElementException("bst is empty!cannot removeMin");}TreeNode minNode = findMinNode(root);root = removeMin(root);return minNode.val;}private TreeNode removeMin(TreeNode root) {if(root.left==null){TreeNode right = root.right;root.left = root.right = root = null;size--;return right;}root.left = removeMin(root.left);return root;}private TreeNode findMinNode(TreeNode root) {if(root.left==null){return root;}return findMinNode(root.left);} public static void main(String[] args) {MyBinarySearchTree bst = new MyBinarySearchTree();bst.add(41);bst.add(28);bst.add(58);bst.add(15);bst.add(33);bst.add(50);System.out.println(bst.toString());System.out.println(bst.removeMin());System.out.println(bst.min());System.out.println(bst.toString());}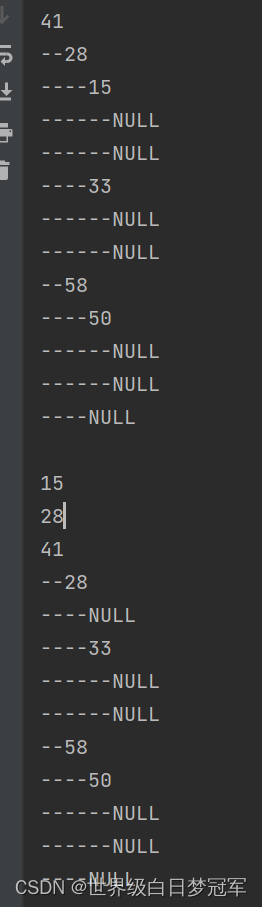
(6)关于最大值
最大值位于右子树的最右侧,一路向右走,碰到第一个root.right == null的结点,root即为最大值结点。
输出最大值和删除最大值和最小值几乎是相同的。
public int max() {if (size == 0) {throw new NoSuchElementException("bst is empty!no max!");}TreeNode maxNode = findMaxNode(root);return maxNode.val;}private TreeNode findMaxNode(TreeNode root) {if(root.right==null){return root;}return findMaxNode(root.right);}public int removeMax() {if (size == 0) {throw new NoSuchElementException("bst is empty!cannot remove max!");}TreeNode maxNode = findMaxNode(root);root = removeMax(root);return maxNode.val;}private TreeNode removeMax(TreeNode root) {if(root.right==null){TreeNode left = root.left;root.left = root = null;size--;return left;}root.right = removeMax(root.right);return root;} public static void main(String[] args) {MyBinarySearchTree bst = new MyBinarySearchTree();bst.add(41);bst.add(28);bst.add(58);bst.add(15);bst.add(33);bst.add(50);System.out.println(bst.toString());System.out.println(bst.removeMax());System.out.println(bst.toString());System.out.println(bst.max());}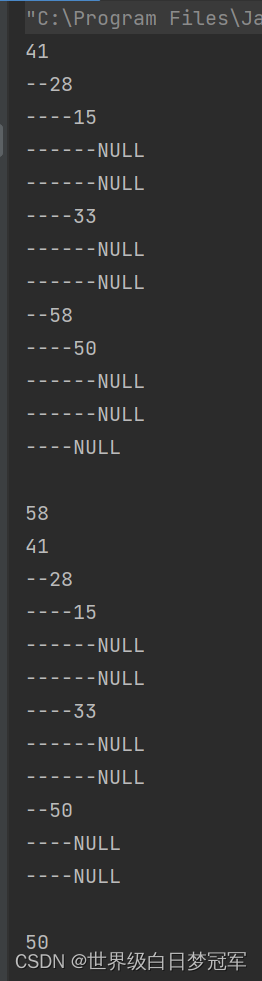
(7)删除任意结点
首先在public的remove方法中判断一下这个key值是否存在,存在则能删除则调用remove(root,key),不存在则直接返回false即可。
在private的remove方法中有四种情况,第一种是root==null,则直接返回null值。第二种是root.val==key,也就是我们找到了需要删除的结点,这时又分为三种情况,如果他的左节点为空,那么直接将右节点补上即可。如果右节点为空那么直接将左节点补上即可。剩下一种情况便是左右节点都不为空,即选择右子树中最小的结点进行填补,在下面的画图中会讲解。
然后当root.val<key,我们调用root.right = remove(root.right,key)即可。剩下的情况即root.val>key调用root.left = remove(root.left,key)即可。
当我们进行一次一个的遍历,root.val == key时,开始进行右子树中最小节点填补的操作。
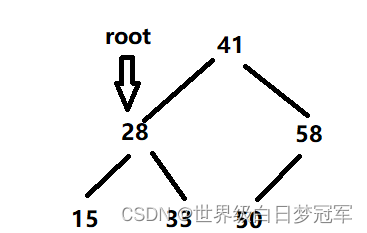
我们需要先行创建一个TreeNode类型的successor变量来存储findMinNode(root.right)中找到的最小值节点。
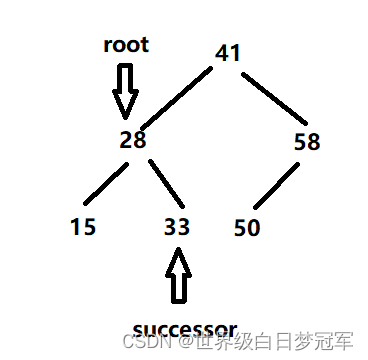
然后使successor.right = removeMin(root.right),即删除最小节点后的root的右子树(在这里为空。)

然后让successor.left = root.left。让successor左节点连接上root的左节点。

再使root的左右节点以及本身置空 root.left = root.right = root = null。最后返回return successor即可,让他与前面的节点连接上。

public boolean remove(int key) {if(!contains(key)){return false;}else{root = remove(root,key);return true;}}private TreeNode remove(TreeNode root, int key) {if(root==null){return null;}if(root.val==key){if(root.left==null){TreeNode right = root.right;root.right = root = null;size--;return right;}else if(root.right==null){TreeNode left = root.left;root.left = root = null;size--;return left;}else{TreeNode successor = findMinNode(root.right);successor.right = removeMin(root.right);successor.left = root.left;root.left = root.right = root = null;return successor;}}else if(root.val<key){root.right = remove(root.right,key);}else {root.left = remove(root.left,key);}return root;} public static void main(String[] args) {MyBinarySearchTree bst = new MyBinarySearchTree();bst.add(41);bst.add(28);bst.add(58);bst.add(15);bst.add(33);bst.add(50);System.out.println(bst.toString());System.out.println(bst.remove(28));System.out.println(bst.toString());}