1. 最优状态估计
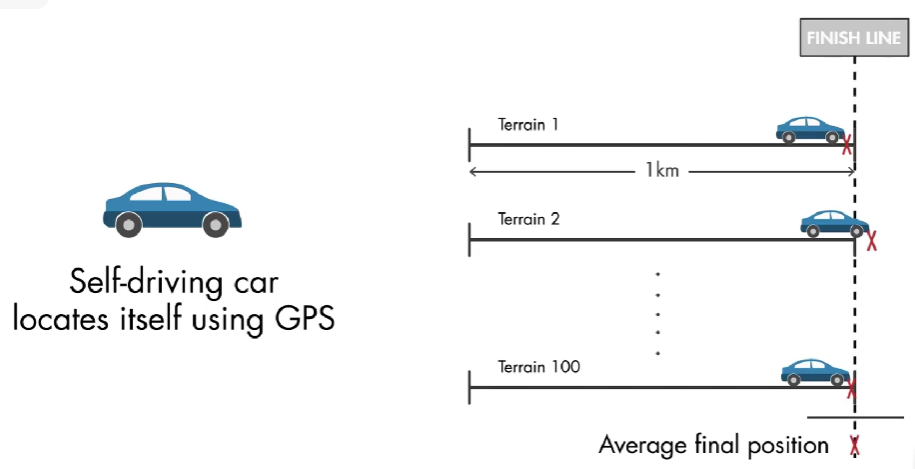
情景1:假设一个一个比赛中,不同队伍的自动驾驶汽车使用 GPS 定位,在 100 种不同的地形上各行驶 1 公里。每次都尽可能停在终点。然后计算每只队伍的平均最终位置。
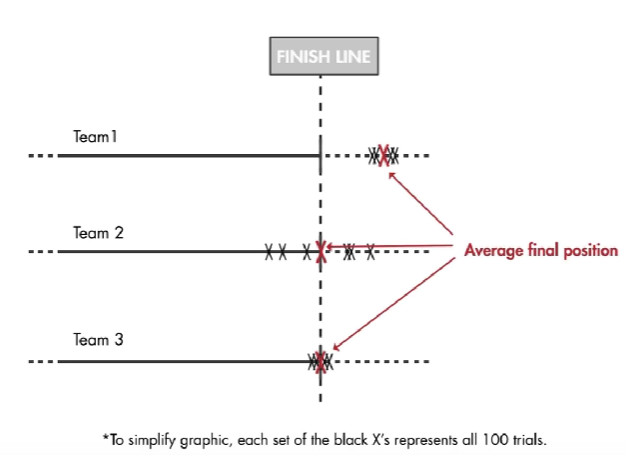
第一组输了:因为虽然方差小,但是偏差大。
第二组输了:因为偏差小,但是方差大
第三组赢了:偏差和方差都小
不能仅仅依靠 GPS 数据,因为它可能有噪声。
目的是:0 偏差 + 最小的方差
可以使用 卡尔曼滤波器。
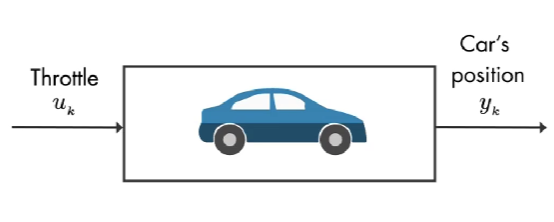
输入是 油门, 输出是 汽车的位置。该系统有多个状态,如下图:

我们简化为:
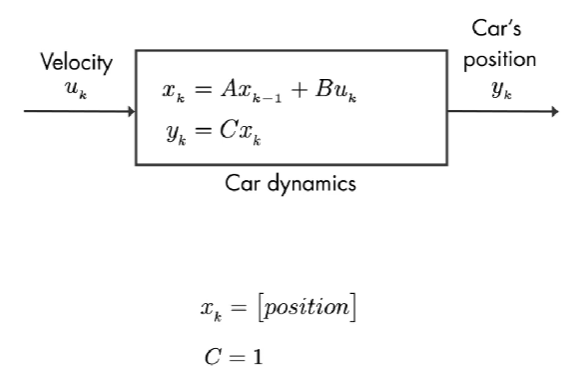
汽车的输入为 速度,该系统只有一个状态: 汽车的位置。我们正在测量这个状态,因此矩阵 C = 1。

GPS 读数有噪音,用 v 表示测量噪声,这是一个随机变量。用 w 表示 过程噪声,也是随机变量,代表风的影响或者汽车速度的变化。虽然这些随机变量不遵循 模式,但是可以使用概率论描述它们的平均属性。
假设 v 服从 0 均值,协方差 R 的高斯分布。因为是单输出系统,协方差 R 是标量,且等于 测量噪声的方差。
类似的,过程噪声也是随机的,假设 w 服从 0 均值,协方差 Q 的高斯分布。
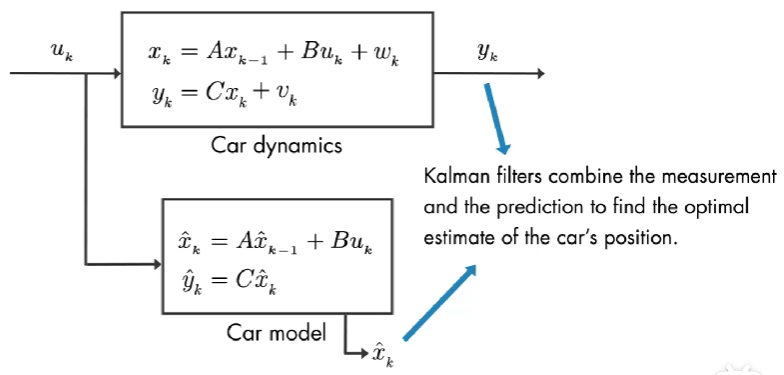
因为,测量是有噪声的,因此,测量的并不能反映汽车的真实位置。如果我们知道汽车模型,我们可以将输入放到模型中来估计位置 x^k\hat{x}_{k}x^k,但是该估计值也不是完美的,因为还有过程噪声也是随机的。卡尔曼滤波结合 测量值 和 模型预测值 来估计汽车的位置。
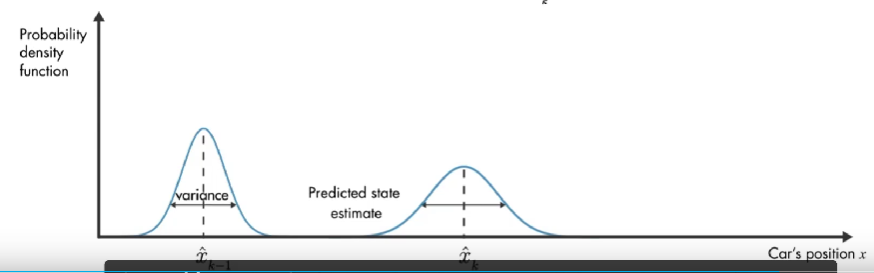
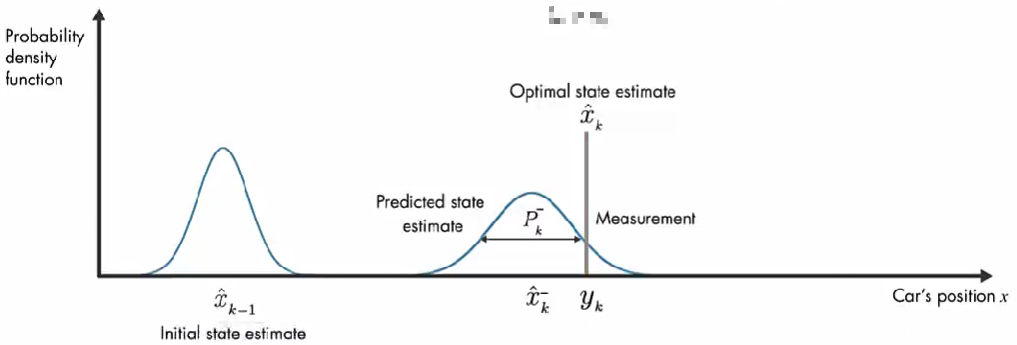
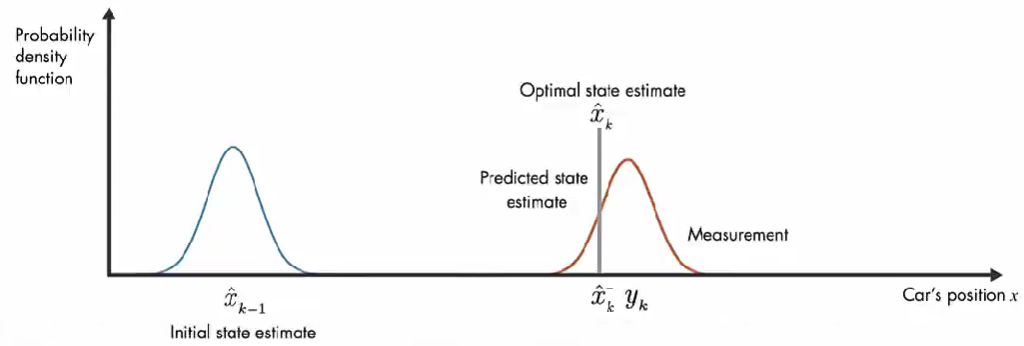
我们使用概率密度函数来直观讨论卡尔曼滤波器的工作原理。在 初始时间 k-1 ,实际汽车位置可能在 模型估计值 x^k−1\hat{x}_{k-1}x^k−1 附近的任何位置,这种不确定性由 概率密度函数描述,汽车最可能在该分布的平均值附近。在下一个时间步,估计的不确定性增大(因为:在时间步 k-1 到 k, 汽车可能经过坑洼,可能车轮打滑,因此可能前进了与 模型估计的距离不同的距离。), 用较大的方差表示。
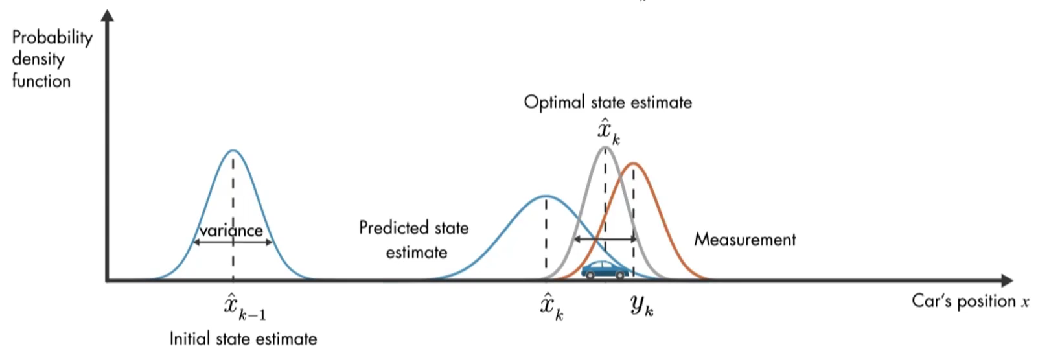
除了数学模型的预测,还有另外一个信息来源:GPS 测量值。上图橙色的高斯分布表示测量的分布,方差表示测量噪声的不确定性,同样,真正的位置可能是该分布平均值的任何位置。
现在有了 预测值 和测量值,那么汽车位置的最优估计是什么?
结合这两部分信息,通过将 预测和测量的 两个概率密度函数相乘,结果也是高斯函数。该高斯的方差小于之前数学模型估计的方差,该高斯的平均值给了我们汽车位置的最优估计。
卡尔曼滤波器可以计算最优无偏差的汽车位置,且方差最小。
2. 最优状态估计算法
状态观测器:(deterministic system)
x^k+1=Ax^k+Buk+K(yk−Cx^k)\hat{x}_{k+1}=A \hat{x}_{k}+B u_{k}+K\left(y_{k}-C \hat{x}_{k}\right)x^k+1=Ax^k+Buk+K(yk−Cx^k)
卡尔曼滤波器:(stochastic system)
x^k=Ax^k−1+Buk+Kk(yk−C(Ax^k−1+Buk))\hat{x}_{k} = A \hat{x}_{k-1}+B u_{k}+K_{k}\left(y_{k}-C\left(A \hat{x}_{k-1}+B u_{k}\right)\right)x^k=Ax^k−1+Buk+Kk(yk−C(Ax^k−1+Buk))
卡尔曼滤波器是一种状态观测器,但是是为 随机系统设计的。
x^k=Ax^k−1+Buk⏟x^k−:APriori Estimate +Kk(yk−C(Ax^k−1+Buk))\hat{x}_{k}=\underbrace{A \hat{x}_{k-1}+B u_{k}}_{\hat{x}_{k}^{-}: A \text { Priori Estimate }}+K_{k}\left(y_{k}-C\left(A \hat{x}_{k-1}+B u_{k}\right)\right)x^k=x^k−:A Priori Estimate Ax^k−1+Buk+Kk(yk−C(Ax^k−1+Buk))
第一步:通过建立的数学模型,使用前一个时间步的预测状态和当前的输入, 预测当前的状态。x^k−\hat{x}_{k}^{-}x^k− 为先验估计,因为计算它的时候没有使用当前的测量值。简化上面等式:
x^k=x^k−+Kk(yk−Cx^k−)\hat{x}_{k}=\hat{x}_{k}^{-}+K_{k}\left(y_{k}-C \hat{x}_{k}^{-}\right)x^k=x^k−+Kk(yk−Cx^k−)
第二步:等式的第二部分使用的是测量值(yky_{k}yk), 代入方程来更新 先验估计, 从而得到后验估计。
x^k⏞APosterioriEstimate=x^k−⏟Predict +Kk(yk−Cx^k−)⏟Update \overset{A Posteriori Estimate}{\overbrace{\hat{x}_{k}}} =\underbrace{\hat{x}_{k}^{-}}_{\text {Predict }}+\underbrace{K_{k}\left(y_{k}-C \hat{x}_{k}^{-}\right)}_{\text {Update }}x^kAPosterioriEstimate=Predict x^k−+Update Kk(yk−Cx^k−)
具体原理:
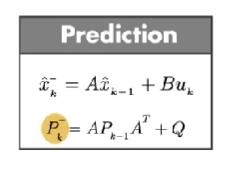
第一步:数学模型预测部分。因为系统状态可能是多个,比如位移、速度等,因为一个系统中大多数的状态信息是相互关联的。对于卡尔曼滤波器这些不同状态的关联性用协方差矩阵(covariance matrix) P 表示。
上图中下面的 Pk−P_{k}^{-}Pk− 计算的是 k 时刻的真实状态 xkx_{k}xk 和 k-1 时刻数学模型预测的 k 时刻的状态 x^k−\hat{x}_{k}^{-}x^k− 之差 的协方差矩阵。
Pk−=cov{xk−x^k−}=cov{Axk−1+Buk+wk−Ax^k−1−−Buk}=cov{A(xk−1−x^k−1−)+wk}=Acov{xk−1−x^k−1−}AT+cov{wk}=APk−1AT+Q
这里会用到:
Cov(AX)=ACov(X)AT\operatorname{Cov}(A X)=A \operatorname{Cov}(X) A^{T}Cov(AX)=ACov(X)AT
推导参考:
- https://www.zhihu.com/question/51082135/answer/150631891
- https://zhuanlan.zhihu.com/p/341440139

对于单状态系统,P 是状态预测值的方差。可以把它当作预测状态中的不确定性的度量,不确定性来自过程误差和预测值 x^k−1\hat{x}_{k-1}x^k−1 的不确定性的影响。
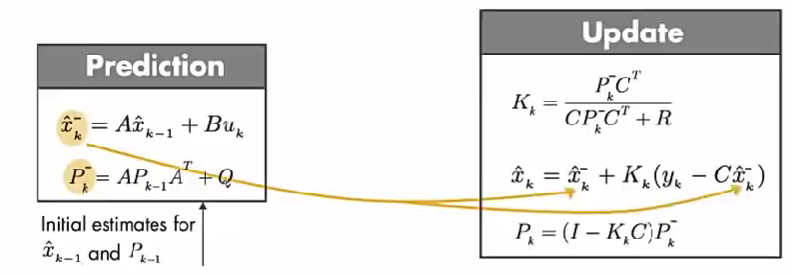
算法的最开始,预测值 x^k−1\hat{x}_{k-1}x^k−1 和 Pk−1P_{k-1}Pk−1 来自初始估计值。
第二步,得到 更新后的状态值 x^k\hat{x}_{k}x^k 和 其 误差协方差 PkP_{k}Pk。推导见上面公式2。
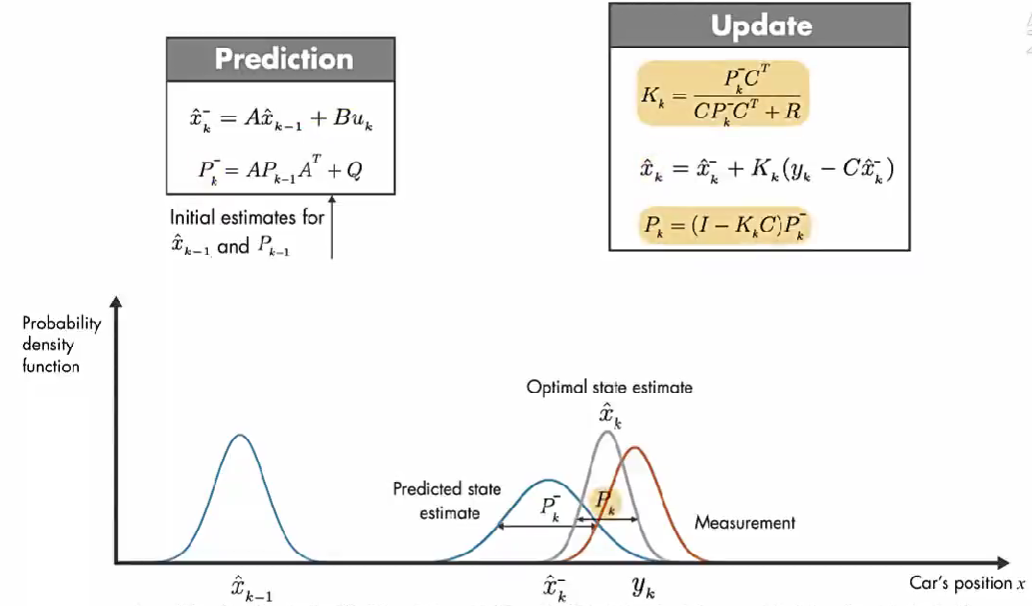
调整卡尔曼增益 KkK_kKk 使得更新后的状态值误差 PkP_{k}Pk 最小。
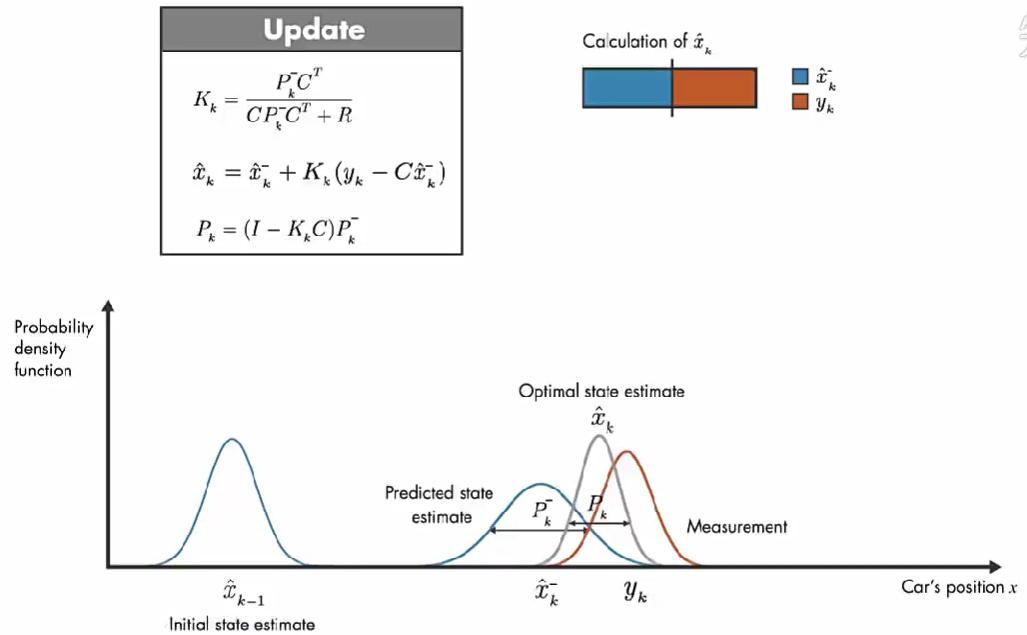
假设上面条表示估算值 x^k\hat{x}_{k}x^k 的计算,通过调整 卡尔曼增益 确定测量值和模型预测值对计算 x^k\hat{x}_{k}x^k 的影响。
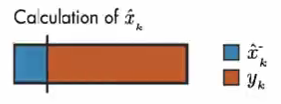
如果测量误差很小,那么测量值更可靠,则应对 x^k\hat{x}_{k}x^k 的计算共享更大。
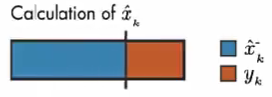
相反,如果模型预测值的误差很小,则模型预测值更可靠,则 x^k\hat{x}_{k}x^k 的计算更多的取决于 模型预测值。
以两种极端情况为例:
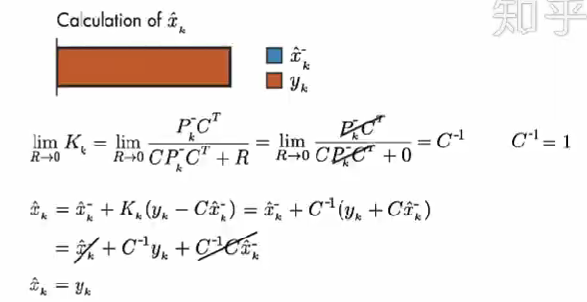
情况1: 假设 测量误差的协方差 R 趋近于 0。我们的上面描述的系统中 C=1。因此,计算结果只取决于 测量值。
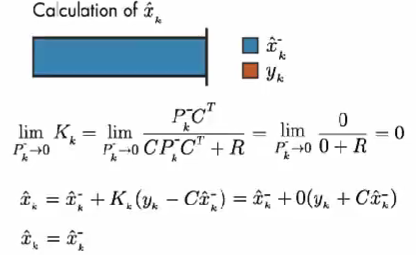
情况2: 如果预测误差协方差趋近于 0。则卡尔曼增益为 0。因此,计算结果只取决于 模型预测值。
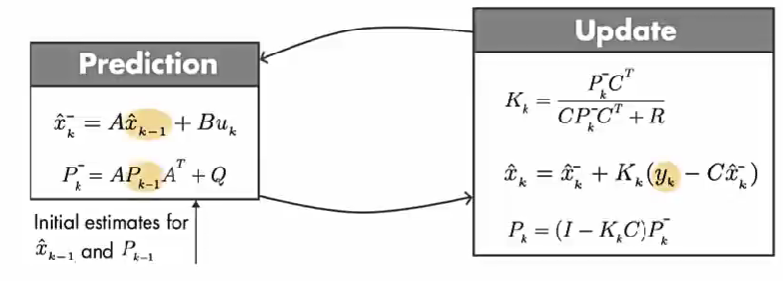
卡尔曼滤波器只需要知道 模型预测状态值 和 前一个时间步以及当前测量误差协方差矩阵。因此 卡尔曼滤波器是递归的。

卡尔曼滤波器 也被称为传感器融合算法。因此可以增加另外一个数据源,比如 IMU。如果有两个测量值 y。K 和 C 的矩阵维度将如上图变化。

将三个概率密度函数相乘来找到汽车位置的最优估计值。
以上讨论都是针对线性系统而言。下面将讨论非线性系统如何使用 卡尔曼滤波器。
参考:
如何通俗并尽可能详细地解释卡尔曼滤波?



![[附源码]计算机毕业设计人体健康管理appSpringboot程序](https://img-blog.csdnimg.cn/ac5fad3e96844184a2ef4186c86dd463.png)