一、前言

前面我们学习了前馈神经网络、卷积神经网络，它们有一个特点，就是每次输出跟上一次结果没有关联。但在一个句子中，每个词的顺序搭配是存在一定联系的，这个时候我们就需要考虑上一次提取的特征对本次输出的影响。这就是我们今天要学的循环神经网络（RNN），也叫递归神经网络，RNN被广泛地应用于自然语言处理（NLP）等领域。

二、序列模型

我们来看一个例子：

我昨天上学迟到了，老师批评了____。

空格里这个词最有可能是『我』，而不太可能是『小明』，甚至是『吃饭』。

这是由上下文推导出来的，这种输出与上下文相互关联的模型，叫做序列模型。

序列模型能够应用在许多领域，例如：

语音识别
音乐发生器
情感分类
DNA序列分析
机器翻译
视频动作识别
命名实体识别

三、不含序列关联的神经网络

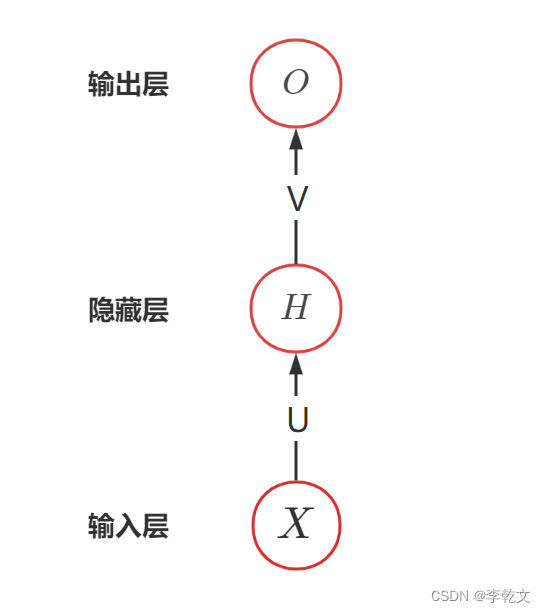
在这里插入图片描述
为简化描述，我们不考虑偏置 $b$ ，如上图所示是包含一个隐藏层的神经网络。 $X$ 表示输入、 $O$ 表示输出； $U$ 是输入层到隐藏层的权重矩阵， $V$ 是隐藏层到输出层的权重矩阵。

设隐藏层的激活函数为 $f$ 、输出层的激活函数为 $g$ ，则有：
$\\O=g(VH)$

四、包含隐藏状态的卷积神经网络

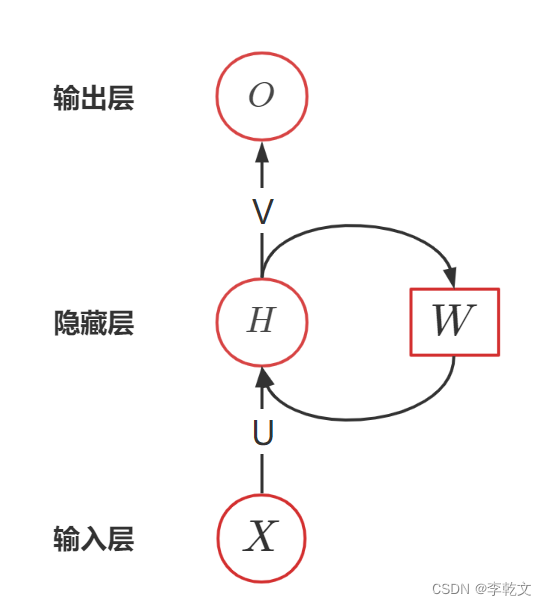
隐藏层的作用，其实就是对输入进行特征值提取，比如卷积神经网络中的卷积层就是对图像边缘的提取。如果说上一次的特征，会对本次特征提取造成一定影响，那怎么表示呢？

我们引入权重参数 $W$ ， $H_{t-1}$ 表示上次特征，用 $WH_{t-1}$ 表示上次特征对本次的影响程度。那么就有本次特征 $H_t=f(UX_t+WH_{t-1})$
本次特征的值不仅取决于本次输入 $X_t$ ，还受上次特征 $H_{t-1}$ 的影响。

这就是RNN的算法思想，用下图表示：
在这里插入图片描述

五、正余弦预测实战

import torch
import torch.nn as nn
import numpy as np
np.set_printoptions(suppress=True) #numpy不使用科学计数法steps=1000   #迭代次数
learning_rate=0.01  #学习率
time_step=10    #步数大小
input_size=1    #输入特征数量
hidden_size=32  #隐藏层特征数量class MyModel(nn.Module):def __init__(self):super().__init__()self.rnn=nn.RNN(input_size=input_size,hidden_size=hidden_size,num_layers=1,batch_first=True)self.out=nn.Linear(hidden_size, 1)def forward(self,x,h_state):r_out,h_state=self.rnn(x,h_state)outs = []for time_step in range(r_out.size(1)):    # 计算每个时间步的输出outs.append(self.out(r_out[:, time_step, :]))return torch.stack(outs, dim=1), h_stateplt_steps=[]
plt_loss=[]h_state = Nonemodel=MyModel()
#损失函数
cost=nn.MSELoss()
#迭代优化器
optmizer=torch.optim.SGD(model.parameters(),lr=learning_rate)step_now,step_x,sin_y,cos_y=None,None,None,None 
for step in range(steps):step_now=stepstep_x=np.linspace(step*np.pi,(step+1)*np.pi,time_step,dtype=np.float32) #起始值、结束值、个数sin_y=np.sin(step_x)cos_y=np.cos(step_x)x = torch.from_numpy(sin_y[np.newaxis, :, np.newaxis])    # shape (batch, time_step, input_size)y = torch.from_numpy(cos_y[np.newaxis, :, np.newaxis])pre_y,h_state=model(x,h_state)h_state = h_state.data#计算损失值loss=cost(pre_y,y)#在反向传播前先把梯度清零optmizer.zero_grad()#反向传播,计算各参数对于损失loss的梯度loss.backward()#根据刚刚反向传播得到的梯度更新模型参数optmizer.step()plt_steps.append(step)plt_loss.append(loss.item())#打印损失值if step%100==0:print('step:',step,'loss:',loss.item())#绘制迭代次数与损失函数的关系
import matplotlib.pyplot as plt
plt.plot(plt_steps,plt_loss)

运行结果：

step: 0 loss: 0.5253313779830933
step: 100 loss: 0.1194605678319931
step: 200 loss: 0.0004494489112403244
step: 300 loss: 0.0004530779551714659
step: 400 loss: 0.00045654349378310144
step: 500 loss: 0.00045824996777810156
step: 600 loss: 0.00045904534636065364
step: 700 loss: 0.0004583548288792372
step: 800 loss: 0.00045726861571893096
step: 900 loss: 0.00045428838348016143

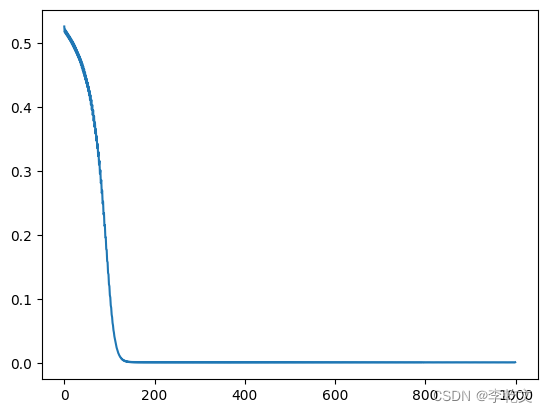
在这里插入图片描述
预测下一段数据结果:

step_x=np.linspace((step_now+1)*np.pi,(step_now+2)*np.pi,time_step,dtype=np.float32) #起始值、结束值、个数
sin_y=np.sin(step_x)
cos_y=np.cos(step_x)x = torch.from_numpy(sin_y[np.newaxis, :, np.newaxis])    # shape (batch, time_step, input_size)
y = torch.from_numpy(cos_y[np.newaxis, :, np.newaxis])pre_y,h_state=model(x,h_state)plt.plot(step_x,sin_y,label='input (sin)')
plt.plot(step_x,cos_y,label='target (cos)')
plt.plot(step_x,pre_y.data.numpy().flatten(),label='pre_y')
plt.legend() #展示标签
plt.show()