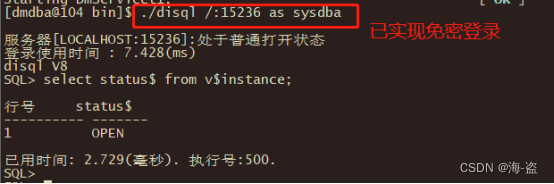
题意:你要输入一篇n个字的文章,每到i+0.1s时可以输入一个字符,每到i+0.9s时有p的概率会奔溃,回到开头或者上一个存盘点,每到第i秒有一次机会可以选择按x个健存盘或者不存,打印完整篇文章之后必须存盘一次才能算完成,求打完之后的最小期望
思路:令dp[i]为打完i个字符的期望,那么不考虑存盘的情况下有dp[i]=dp[i-1]+p*(1+dp[i])+(1-p),意思是要考虑第i个字符,首先前提是i-1个字符要打完了,然后有两种情况就是奔溃了那么要再打i个字符或者不奔溃,然后枚举存盘的时间就行了
#include<bits/stdc++.h>
using namespace std;
const int maxn = 100005;
#define INF 1e9
double dp[maxn];
int main()
{int T;int cas = 1;scanf("%d",&T);while (T--){int n,x;double p;scanf("%d%lf%d",&n,&p,&x);for (int i = 1;i<=n;i++)dp[i]=(dp[i-1]+1)/(1-p);double ans = INF;for (int i = 1;i<=n;i++){int a = n/i;int b = n%i;ans = min(ans,dp[a+1]*b+dp[a]*(i-b)+x*i);}printf("Case #%d: %.6lf\n",cas++,ans);}
}
Problem Description
As the term is going to end, DRD begins to write his final article.
DRD uses the famous Macrohard's software, World, to write his article. Unfortunately this software is rather unstable, and it always crashes. DRD needs to write n characters in his article. He can press a key to input a character at time i+0.1 , where i is an integer equal or greater than 0. But at every time i−0.1 for integer i strictly greater than 0, World might crash with probability p and DRD loses his work, so he maybe has to restart from his latest saved article. To prevent write it again and again, DRD can press Ctrl-S to save his document at time i . Due to the strange keyboard DRD uses, to press Ctrl-S he needs to press x characters. If DRD has input his total article, he has to press Ctrl-S to save the document.
Since World crashes too often, now he is asking his friend ATM for the optimal strategy to input his article. A strategy is measured by its expectation keys DRD needs to press.
Note that DRD can press a key at fast enough speed.
DRD uses the famous Macrohard's software, World, to write his article. Unfortunately this software is rather unstable, and it always crashes. DRD needs to write n characters in his article. He can press a key to input a character at time i+0.1 , where i is an integer equal or greater than 0. But at every time i−0.1 for integer i strictly greater than 0, World might crash with probability p and DRD loses his work, so he maybe has to restart from his latest saved article. To prevent write it again and again, DRD can press Ctrl-S to save his document at time i . Due to the strange keyboard DRD uses, to press Ctrl-S he needs to press x characters. If DRD has input his total article, he has to press Ctrl-S to save the document.
Since World crashes too often, now he is asking his friend ATM for the optimal strategy to input his article. A strategy is measured by its expectation keys DRD needs to press.
Note that DRD can press a key at fast enough speed.
Input
First line: an positive integer 0≤T≤20 indicating the number of cases.
Next T lines: each line has a positive integer n≤105 , a positive real 0.1≤p≤0.9 , and a positive integer x≤100 .
Next T lines: each line has a positive integer n≤105 , a positive real 0.1≤p≤0.9 , and a positive integer x≤100 .
Output
For each test case: output ''Case #k: ans'' (without quotes), where k is the number of the test cases, and ans is the expectation of keys of the optimal strategy.
Your answer is considered correct if and only if the absolute error or the relative error is smaller than 10−6 .
Your answer is considered correct if and only if the absolute error or the relative error is smaller than 10−6 .
Sample Input
2 1 0.5 2 2 0.4 2
Sample Output
Case #1: 4.000000 Case #2: 6.444444