物以类聚，人以群分；近朱者赤，近墨者黑。这两句话的大概意思就是，你周围大部分朋友是什么人，那么你大概率也就是这种人，这句话其实也就是KNN算法的核心思想。

所谓的物以类聚，人以群分，我们需要量化样本之间的差距，我们先来看看几个公式

1，欧几里得距离
欧几里得距离是运用最广的一种计算距离的方式，我们从小在课本上接触到的也是这个东西，它衡量的是多维空间中两点之间的绝对距离，表达式如下：

2，明可夫斯基距离
明可夫斯基距离是一种对多种距离的概括性描述，其表达式如下 ：

3，曼哈顿距离（Manhattan distance）
当p=1时，得到绝对值距离，也称曼哈顿距离，表达式如下：

4，切比雪夫距离（Chebyshev Distance）
当p->∞时，得到切比雪夫距离。表达式如下： 

二，算法原理

      如果一个样本在特征空间中的k个最相似的样本中属于某一类，则该样本也属于这个类别。KNN算法中，所选择的邻居都是分好类的

  

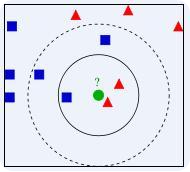
就假设我们的正方形，三角形都是已知的类别，从上图我们可以看到圆形这个最有可能的分类就是三角形了，当然这也可能是它伪装的太好了，我们已知的几个特征点都和三角形太相近了，这时我们可以搜集更多的特征点，去对未知类别分类。

由于KNN最邻近分类算法在分类决策时只依据最邻近的一个或者几个样本的类别来决定待分类样本所属的类别，而不是靠判别类域的方法来确定所属类别的，因此对于类域的交叉或重叠较多的待分样本集来说，KNN方法较其他方法更为适合。

因此，k值的选择、距离度量以及分类决策规则是k近邻算法的三个基本要素。

k近邻中的分类决策规则往往就是多数表决，既由输入实例的k个近邻的训练中的多数类决定输入类决定输入实例的类。

具体代码可以观看下面这篇博客

knn约会网站实例https://blog.csdn.net/gf_lvah/article/details/89355051?ops_request_misc=&request_id=&biz_id=102&utm_term=knn%E7%BA%A6%E4%BC%9A%E7%BD%91%E7%AB%99%20gf_lvah&utm_medium=distribute.pc_search_result.none-task-blog-2~all~sobaiduweb~default-0-89355051.142%5Ev9%5Epc_search_result_control_group,157%5Ev4%5Econtrol&spm=1018.2226.3001.4187

需要数据了，可以联系我 

我们知道KNN是基于距离的一个简单分类算法，熟悉KNN的都知道，我们要不断计算两个样本点之间的距离，但是，试想一下，如果数据量特别大的时候，我们要每个都计算一下，那样计算量是非常大的，所以提出了一种优化KNN的算法-----kd-tree.

实现k近邻法时，主要考虑的问题是如何对训练数据进行快速k近邻搜索。这在特征空间的维数大及训练数据容量大时尤其必要。k近邻法最简单的实现是线性扫描（穷举搜索），即要计算输入实例与每一个训练实例的距离。计算并存储好以后，再查找K近邻。当训练集很大时，计算非常耗时。为了提高kNN搜索的效率，可以考虑使用特殊的结构存储训练数据，以减小计算距离的次数。

kd树(K-dimension tree)是一种对k维空间中的实例点进行存储以便对其进行快速检索的树形数据结构。kd树是是一种二叉树，表示对k维空间的一个划分，构造kd树相当于不断地用垂直于坐标轴的超平面将K维空间切分，构成一系列的K维超矩形区域。kd树的每个结点对应于一个k维超矩形区域。利用kd树可以省去对大部分数据点的搜索，从而减少搜索的计算量。