红黑树

红黑树介绍

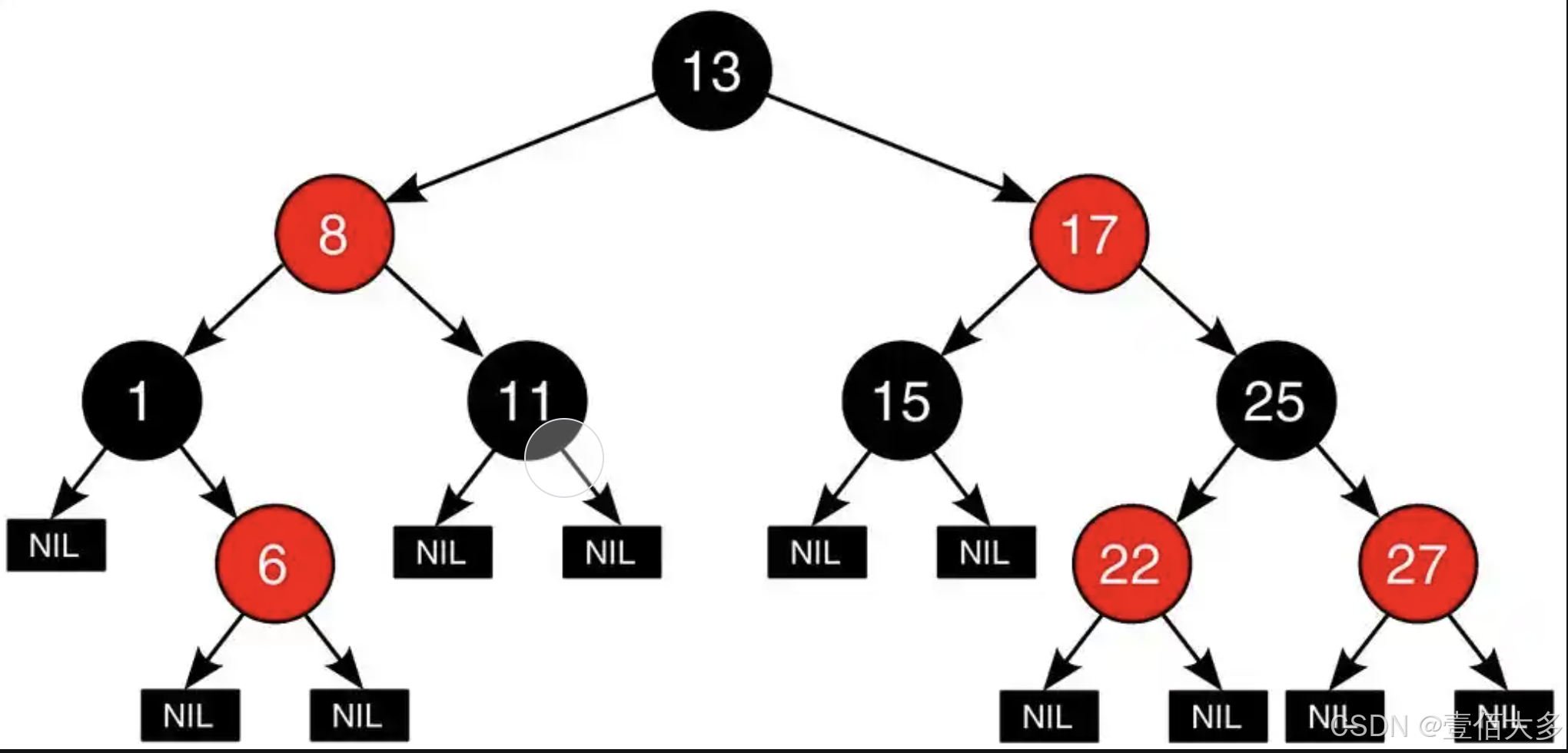
红黑树（Red-Black Tree）是一种自平衡的二叉查找树（Binary Search Tree, BST），它在普通二叉查找树的基础上增加了一些额外的约束条件，以确保树的平衡性，从而保证在最坏情况下插入、删除和查找操作的时间复杂度为 O(logn)。

红黑树的五个基本性质

红黑树是一种特殊的二叉查找树，它满足以下五个基本性质：
1.节点是红色或黑色，每个节点都有一个颜色属性，红色或黑色。
2.根节点必须是黑色
3.叶子节点（即空节点或 null）是黑色。
4.如果一个节点是红色，则它的两个子节点都是黑色。换句话说，红色节点不能连续出现。
5.从任意节点到其每个叶子节点的所有路径上，黑色节点的数量相同。这一性质确保了树的平衡性。

红黑树的平衡原理

红黑树通过上述性质来保证树的平衡。虽然红黑树不是完全平衡的二叉树，但它能够保证最长路径和最短路径的长度不会相差太大。具体来说，红黑树的最长路径不会超过最短路径的两倍，从而保证了树的近似平衡。

红黑树的操作

红黑树的主要操作包括插入、删除和查找。这些操作在普通二叉查找树的基础上增加了颜色调整和旋转操作，以确保树的平衡。

红黑树的操作

红黑树的主要操作包括插入、删除和查找。这些操作在普通二叉查找树的基础上增加了颜色调整和旋转操作，以确保树的平衡。
插入操作
插入新节点：将新节点插入到树中，新节点默认为红色。
修复树的性质：插入后可能违反红黑树的性质，需要通过以下操作修复：
颜色翻转：改变节点的颜色。
旋转操作：包括左旋和右旋，调整树的结构。
删除操作
删除节点：删除目标节点。
修复树的性质：删除后可能违反红黑树的性质，需要通过以下操作修复：
颜色调整：改变节点的颜色。
旋转操作：调整树的结构。
查找操作
查找操作与普通二叉查找树相同，从根节点开始，根据键值的大小关系逐层向下查找，直到找到目标节点或到达叶子节点。

代码实现

节点实现

class Node<K extends Comparable<K>, V> {K key;V value;Node<K, V> left, right, parent;boolean color; // true 表示红色，false 表示黑色public Node(K key, V value) {this.key = key;this.value = value;this.color = true; // 新节点默认为红色}
}

插入和查询操作

public class RedBlackTree<K extends Comparable<K>, V> {private Node<K, V> root;// 插入操作public void insert(K key, V value) {root = insert(root, key, value);root.color = false; // 根节点必须是黑色}private Node<K, V> insert(Node<K, V> node, K key, V value) {if (node == null) {return new Node<>(key, value);}if (key.compareTo(node.key) < 0) {node.left = insert(node.left, key, value);node.left.parent = node;} else if (key.compareTo(node.key) > 0) {node.right = insert(node.right, key, value);node.right.parent = node;} else {node.value = value; // 如果键已存在，更新值}// 修复红黑树性质return fixAfterInsertion(node);}// 修复插入后的红黑树性质private Node<K, V> fixAfterInsertion(Node<K, V> node) {while (node != null && node != root && node.parent.color) {if (node.parent == node.parent.parent.left) {Node<K, V> uncle = node.parent.parent.right;if (uncle != null && uncle.color) {// 情况1：叔叔节点是红色node.parent.color = false;uncle.color = false;node.parent.parent.color = true;node = node.parent.parent;} else {if (node == node.parent.right) {// 情况2：右倾，先左旋node = node.parent;rotateLeft(node);}// 情况3：左倾，右旋node.parent.color = false;node.parent.parent.color = true;rotateRight(node.parent.parent);}} else {Node<K, V> uncle = node.parent.parent.left;if (uncle != null && uncle.color) {// 情况1：叔叔节点是红色node.parent.color = false;uncle.color = false;node.parent.parent.color = true;node = node.parent.parent;} else {if (node == node.parent.left) {// 情况2：左倾，先右旋node = node.parent;rotateRight(node);}// 情况3：右倾，左旋node.parent.color = false;node.parent.parent.color = true;rotateLeft(node.parent.parent);}}}return node;}// 左旋操作private void rotateLeft(Node<K, V> x) {Node<K, V> y = x.right;x.right = y.left;if (y.left != null) {y.left.parent = x;}y.parent = x.parent;if (x.parent == null) {root = y;} else if (x == x.parent.left) {x.parent.left = y;} else {x.parent.right = y;}y.left = x;x.parent = y;}// 右旋操作private void rotateRight(Node<K, V> x) {Node<K, V> y = x.left;x.left = y.right;if (y.right != null) {y.right.parent = x;}y.parent = x.parent;if (x.parent == null) {root = y;} else if (x == x.parent.right) {x.parent.right = y;} else {x.parent.left = y;}y.right = x;x.parent = y;}// 查找操作public V get(K key) {Node<K, V> node = root;while (node != null) {int cmp = key.compareTo(node.key);if (cmp < 0) {node = node.left;} else if (cmp > 0) {node = node.right;} else {return node.value;}}return null;}
}

代码说明
节点定义：
每个节点包含键、值、左右子节点和父节点指针，以及一个颜色属性（红色或黑色）。
插入操作：
插入新节点时，新节点默认为红色。
插入后调用 fixAfterInsertion 方法修复红黑树的性质。
修复逻辑：
根据红黑树的性质，修复插入操作可能破坏的平衡。
主要处理以下几种情况：
叔叔节点是红色：将父节点和叔叔节点改为黑色，祖父节点改为红色，继续向上检查。
叔叔节点是黑色：根据节点的位置进行旋转操作，调整树的结构。
旋转操作：
左旋：将右子节点提升为新的根节点，调整子树的连接关系。
右旋：将左子节点提升为新的根节点，调整子树的连接关系。
查找操作：
从根节点开始，根据键值的大小关系逐层向下查找，直到找到目标节点或到达叶子节点。