蓝桥杯算法笔记|前缀和3382、3419

news/2025/1/30 20:49:58/

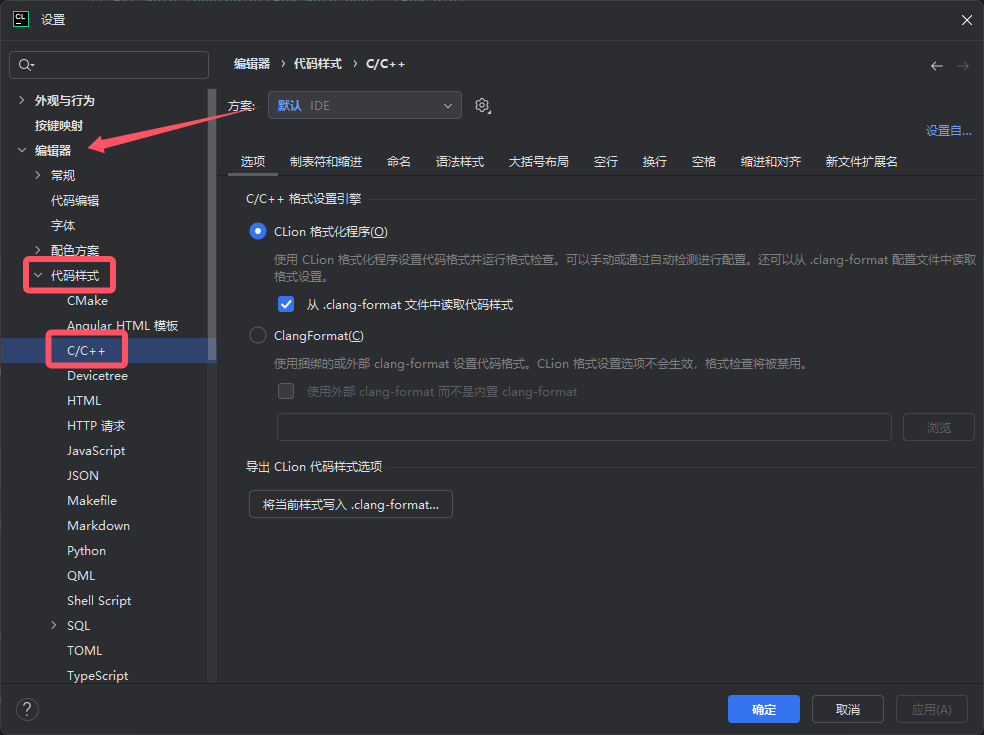
！前倾回顾

（一）进制转换

任意进制转化成十进制

int x=0;//存放结果
int k;//k存放当前进制
int a[];//存放当前数拆解成的每位数
for(int i=0;i<a.size();i++){x=x*k+a[i];
}
cout<<x<<'\n'

十进制转化成任意进制

string s;//存放结果
//已知十进制x
int k,i=0;//转化成K进制
int ch[]={'1','2','3','4','5','6','7','8','9','A','B','C','D','E','F'};
while(x){s[i]=x%k;x=x/k;
}
reverse(s.begin(),s.end());
count<<s<<'\n';

一、前缀和

在C++中，前缀和（Prefix Sum）技术通常用于加速某些类型的查询或计算，特别是在处理数组或序列时。这种技术特别适用于需要频繁查询某个区间内元素之和的问题。下面是一些关于如何理解和使用前缀和的指导：

什么是前缀和？

前缀和指的是对于一个给定的数组arr[]，创建一个新的数组prefixSum[]，其中prefixSum[i]是原数组从第一个元素到第i个元素（包含）的所有元素之和。

例如，给定数组arr = {1, 2, 3, 4, 5}，其对应的前缀和数组prefixSum将是{1, 3, 6, 10, 15}。

如何构建前缀和数组？

假设你有一个数组arr[]，你可以通过以下方式构建前缀和数组prefixSum[]：
int arr[] = {1, 2, 3, 4, 5};
int n = sizeof(arr)/sizeof(arr[0]);
int prefixSum[n];prefixSum[0] = arr[0];
for(int i = 1; i < n; ++i){prefixSum[i] = prefixSum[i-1] + arr[i];
}
应用场景

快速求解区间和：给定两个索引i和j，要找到从i到j之间所有元素的和，可以简单地使用prefixSum[j] - prefixSum[i-1]（如果i > 0），或者直接为prefixSum[j]（如果i == 0）。这使得原本可能需要O(n)时间复杂度的操作降低到了O(1)，前提是前缀和数组已经被计算好。
优化动态规划问题：在某些情况下，利用前缀和可以在状态转移方程中减少重复计算，从而优化算法性能。
二维前缀和：在处理二维数组时，可以通过类似的思路计算二维前缀和，以便于快速查询子矩阵的和。

二、前缀和题目练习

题目：https://www.lanqiao.cn/problems/3382/learning

解题误区：

每次都重新K次方，超时！！！
直接将1~5所有的次方情况一次算出来！这些次方数像前缀和和一样不会因为输入的数值而改变。

解题代码：

(太裂开了这道题，折磨了我一下午，下边是参考着敲的最优解)

#include<bits/stdc++.h>
#include<cmath>
using namespace std;
const long Q=1e9+7;
int main(){int n,m;cin>>n>>m;int a[n];//必须输入了n之后才能定义a【n】，最后卡在了这里for(int i=0;i<n;i++){cin>>a[i]; }long long sum[6][n+1];//算sum前缀和 //1、既实现了K次方，又实现了求前缀和，取模 //2、注意，这里的i是 for(int i=1;i<6;i++){for(int j=1;j<=n;j++){sum[i][j]=sum[i][j-1]+pow(a[j-1],i);sum[i][j]=sum[i][j]%Q;} } for(int i=0;i<m;i++){int l,r,k;cin>>l>>r>>k;long res=(sum[k][r]+Q-sum[k][l-1])%Q;cout<<res<<'\n';} return 0;
}