prim算法精讲
https://www.programmercarl.com/kamacoder/0053.%E5%AF%BB%E5%AE%9D-prim.html
prim算法核心就是三步,熟悉这三步,代码相对会好些很多:
- 第一步,选距离生成树最近节点
- 第二步,最近节点加入生成树
- 第三步,更新非生成树节点到生成树的距离(即更新minDist数组)
在prim算法中,有一个数组特别重要,这里起名为:minDist。
“每次寻找距离 最小生成树最近的节点 并加入到最小生成树中”,那么如何寻找距离最小生成树最近的节点呢?
这就用到了 minDist 数组, 它用来作什么呢?
minDist数组 用来记录 每一个节点距离最小生成树的最近距离。 理解这一点非常重要,这也是 prim算法最核心要点所在
1 初始状态
minDist 数组 里的数值初始化为 最大数,因为本题 节点距离不会超过 10000,所以 初始化最大数为 10001就可以。
现在 还没有最小生成树,默认每个节点距离最小生成树是最大的,这样后面我们在比较的时候,发现更近的距离,才能更新到 minDist 数组上。
开始构造最小生成树
2
1、prim三部曲,第一步:选距离生成树最近节点
选择距离最小生成树最近的节点,加入到最小生成树,刚开始还没有最小生成树,所以随便选一个节点加入就好(因为每一个节点一定会在最小生成树里,所以随便选一个就好),那我们选择节点1 (符合遍历数组的习惯,第一个遍历的也是节点1)
2、prim三部曲,第二步:最近节点加入生成树
此时 节点1 已经算最小生成树的节点。
3、prim三部曲,第三步:更新非生成树节点到生成树的距离(即更新minDist数组)
接下来,我们要更新所有节点距离最小生成树的距离.
注意下标0,我们就不管它了,下标 1 与节点 1 对应,这样可以避免大家把节点搞混。
此时所有非生成树的节点距离 最小生成树(节点1)的距离都已经跟新了 。
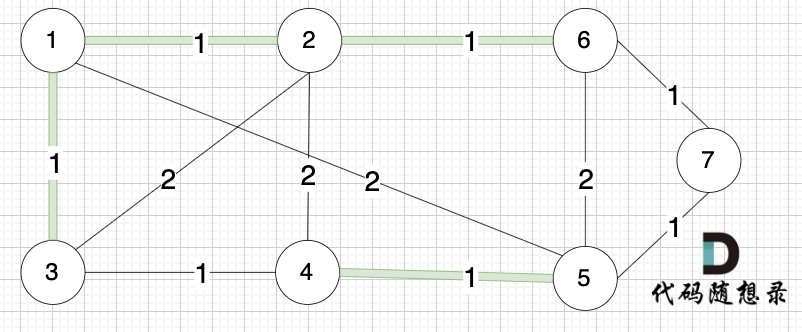
- 节点2 与 节点1 的距离为1,比原先的 距离值10001小,所以更新minDist[2]。
- 节点3 和 节点1 的距离为1,比原先的 距离值10001小,所以更新minDist[3]。
- 节点5 和 节点1 的距离为2,比原先的 距离值10001小,所以更新minDist[5]。
注意图中我标记了 minDist数组里更新的权值,是哪两个节点之间的权值,例如 minDist[2] =1 ,这个 1 是 节点1 与 节点2 之间的连线,清楚这一点对最后我们记录 最小生成树的权值总和很重要。
(我在后面依然会不断重复 prim三部曲,可能基础好的录友会感觉有点啰嗦,但也是让大家感觉这三部曲求解的过程)
3
1、prim三部曲,第一步:选距离生成树最近节点
选取一个距离 最小生成树(节点1) 最近的非生成树里的节点,节点2,3,5 距离 最小生成树(节点1) 最近,选节点 2(其实选 节点3或者节点2都可以,距离一样的)加入最小生成树。
2、prim三部曲,第二步:最近节点加入生成树
此时 节点1 和 节点2,已经算最小生成树的节点。
3、prim三部曲,第三步:更新非生成树节点到生成树的距离(即更新minDist数组)
接下来,我们要更新节点距离最小生成树的距离
此时所有非生成树的节点距离 最小生成树(节点1、节点2)的距离都已经跟新了 。
- 节点3 和 节点2 的距离为2,和原先的距离值1 小,所以不用更新。
- 节点4 和 节点2 的距离为2,比原先的距离值10001小,所以更新minDist[4]。
- 节点5 和 节点2 的距离为10001(不连接),所以不用更新。
- 节点6 和 节点2 的距离为1,比原先的距离值10001小,所以更新minDist[6]。
4
1、prim三部曲,第一步:选距离生成树最近节点
选择一个距离 最小生成树(节点1、节点2) 最近的非生成树里的节点,节点3,6 距离 最小生成树(节点1、节点2) 最近,选节点3 (选节点6也可以,距离一样)加入最小生成树。
2、prim三部曲,第二步:最近节点加入生成树
此时 节点1 、节点2 、节点3 算是最小生成树的节点。
3、prim三部曲,第三步:更新非生成树节点到生成树的距离(即更新minDist数组)
接下来更新节点距离最小生成树的距离,如图:
所有非生成树的节点距离 最小生成树(节点1、节点2、节点3 )的距离都已经跟新了 。
- 节点 4 和 节点 3的距离为 1,和原先的距离值 2 小,所以更新minDist[4]为1。
上面为什么我们只比较 节点4 和 节点3 的距离呢?
因为节点3加入 最小生成树后,非 生成树节点 只有 节点 4 和 节点3是链接的,所以需要重新更新一下 节点4距离最小生成树的距离,其他节点距离最小生成树的距离 都不变。
5
1、prim三部曲,第一步:选距离生成树最近节点
继续选择一个距离 最小生成树(节点1、节点2、节点3) 最近的非生成树里的节点,为了巩固大家对 minDist数组的理解,这里我再啰嗦一遍:
minDist数组 是记录了 所有非生成树节点距离生成树的最小距离,所以 从数组里我们能看出来,非生成树节点 4 和 节点 6 距离 生成树最近。
任选一个加入生成树,我们选 节点4(选节点6也行) 。
注意,我们根据 minDist数组,选取距离 生成树 最近的节点 加入生成树,那么 minDist数组里记录的其实也是 最小生成树的边的权值(我在图中把权值对应的是哪两个节点也标记出来了)。
如果大家不理解,可以跟着我们下面的讲解,看 minDist数组的变化, minDist数组 里记录的权值对应的哪条边。
理解这一点很重要,因为 最后我们要求 最小生成树里所有边的权值和。
2、prim三部曲,第二步:最近节点加入生成树
此时 节点1、节点2、节点3、节点4 算是 最小生成树的节点。
3、prim三部曲,第三步:更新非生成树节点到生成树的距离(即更新minDist数组)
接下来更新节点距离最小生成树的距离,如图:
minDist数组已经更新了 所有非生成树的节点距离 最小生成树(节点1、节点2、节点3、节点4 )的距离 。
- 节点 5 和 节点 4的距离为 1,和原先的距离值 2 小,所以更新minDist[5]为1。
6
1、prim三部曲,第一步:选距离生成树最近节点
继续选距离 最小生成树(节点1、节点2、节点3、节点4 )最近的非生成树里的节点,只有 节点 5 和 节点6。
选节点5 (选节点6也可以)加入 生成树。
2、prim三部曲,第二步:最近节点加入生成树
节点1、节点2、节点3、节点4、节点5 算是 最小生成树的节点。
3、prim三部曲,第三步:更新非生成树节点到生成树的距离(即更新minDist数组)
接下来更新节点距离最小生成树的距离。
minDist数组已经更新了 所有非生成树的节点距离 最小生成树(节点1、节点2、节点3、节点4 、节点5)的距离 。
- 节点 6 和 节点 5 距离为 2,比原先的距离值 1 大,所以不更新
- 节点 7 和 节点 5 距离为 1,比原先的距离值 10001小,更新 minDist[7]
7
1、prim三部曲,第一步:选距离生成树最近节点
继续选距离 最小生成树(节点1、节点2、节点3、节点4 、节点5)最近的非生成树里的节点,只有 节点 6 和 节点7。
2、prim三部曲,第二步:最近节点加入生成树
选节点6 (选节点7也行,距离一样的)加入生成树。
3、prim三部曲,第三步:更新非生成树节点到生成树的距离(即更新minDist数组)
节点1、节点2、节点3、节点4、节点5、节点6 算是 最小生成树的节点 ,接下来更新节点距离最小生成树的距离。
这里就不在重复描述了,大家类推,最后,节点7加入生成树。
最后
最后我们就生成了一个 最小生成树, 绿色的边将所有节点链接到一起,并且 保证权值是最小的,因为我们在更新 minDist 数组的时候,都是选距离 最小生成树最近的点 加入到树中。
讲解上面的模拟过程的时候,我已经强调多次 minDist数组 是记录了 所有非生成树节点距离生成树的最小距离。
最后,minDist数组 也就是记录的是最小生成树所有边的权值。
特别把 每条边的权值对应的是哪两个节点 标记出来(例如minDist[7] = 1,对应的是节点5 和 节点7之间的边,而不是 节点6 和 节点7),为了就是让大家清楚, minDist里的每一个值 对应的是哪条边。
那么我们要求最小生成树里边的权值总和 就是 把 最后的 minDist 数组 累加一起。
思路
#include <stdio.h>
#include <limits.h>
#include <stdbool.h>int main() {int v, e;int x, y, k;scanf("%d %d", &v, &e);// 初始化二维数组,表示图的权重,默认最大值10001int grid[v+1][v+1];for (int i = 1; i <= v; i++) {for (int j = 1; j <= v; j++) {grid[i][j] = 10001;}}// 读取边信息while (e--) {scanf("%d %d %d", &x, &y, &k);grid[x][y] = k;grid[y][x] = k;}// 所有节点到最小生成树的最小距离int minDist[v+1];for (int i = 1; i <= v; i++) {minDist[i] = 10001;}// 这个节点是否在树里bool isInTree[v+1];for (int i = 1; i <= v; i++) {isInTree[i] = false;}// Prim算法构建最小生成树for (int i = 1; i < v; i++) {int cur = -1;int minVal = INT_MAX;// 选择距离生成树最近的节点for (int j = 1; j <= v; j++) {if (!isInTree[j] && minDist[j] < minVal) {minVal = minDist[j];cur = j;}}// 将最近节点加入生成树isInTree[cur] = true;// 更新非生成树节点到生成树的距离for (int j = 1; j <= v; j++) {if (!isInTree[j] && grid[cur][j] < minDist[j]) {minDist[j] = grid[cur][j];}}}// 统计结果int result = 0;for (int i = 2; i <= v; i++) {result += minDist[i];}printf("%d\n", result);return 0;
}学习反思
代码是Prim算法的C实现,用于找到给定图的最小生成树。
该代码包含以下步骤:
从输入中读取顶点数(v)和边数(e)。
初始化一个名为“网格”的二维数组,以表示每对顶点之间的边的权重。将所有值初始化为默认最大值10001。
从输入中读取边及其权重,并相应地更新网格。
创建一个名为“minDist”的数组来存储从每个顶点到最小生成树的最小距离。将所有值初始化为默认最大值。
创建一个名为“isInTree”的数组来存储顶点是否在最小生成树中。将所有值初始化为false。
使用Prim的算法构建最小生成树:a.选择最接近最小生成树的顶点(cur)。b.将所选顶点添加到最小生成树中。c.如果通过所选顶点的路径较短,则更新不在最小生成树中的每个顶点的最小距离。
计算最小生成树中边的权重之和。
打印结果。
总体而言,该代码正确地实现了Prim的算法,以在C中找到给定图的最小生成树。
kruskal算法精讲
https://www.programmercarl.com/kamacoder/0053.%E5%AF%BB%E5%AE%9D-Kruskal.html
在上一篇 我们讲解了 prim算法求解 最小生成树,本篇我们来讲解另一个算法:Kruskal,同样可以求最小生成树。
prim 算法是维护节点的集合,而 Kruskal 是维护边的集合。
上来就这么说,大家应该看不太懂,这里是先让大家有这么个印象,带着这个印象在看下文,理解的会更到位一些。
kruscal的思路:
- 边的权值排序,因为要优先选最小的边加入到生成树里
- 遍历排序后的边
- 如果边首尾的两个节点在同一个集合,说明如果连上这条边图中会出现环
- 如果边首尾的两个节点不在同一个集合,加入到最小生成树,并把两个节点加入同一个集合
下面我们画图举例说明kruscal的工作过程。
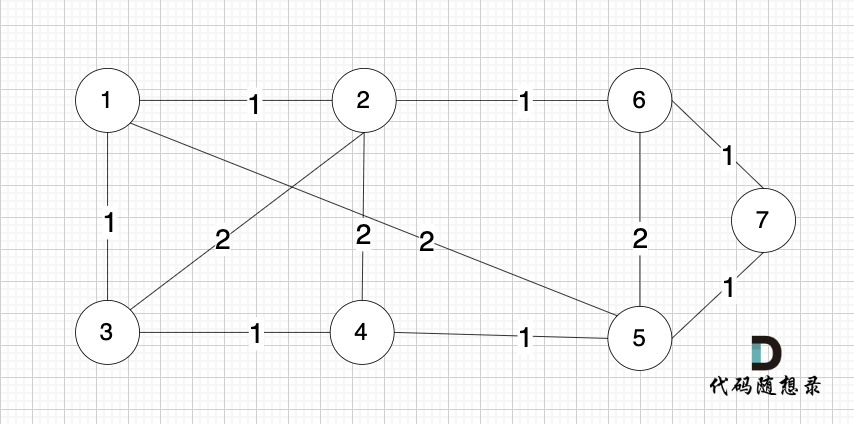
依然以示例中,如下这个图来举例。
将图中的边按照权值有小到大排序,这样从贪心的角度来说,优先选 权值小的边加入到 最小生成树中。
排序后的边顺序为[(1,2) (4,5) (1,3) (2,6) (3,4) (6,7) (5,7) (1,5) (3,2) (2,4) (5,6)]
(1,2) 表示节点1 与 节点2 之间的边。权值相同的边,先后顺序无所谓。
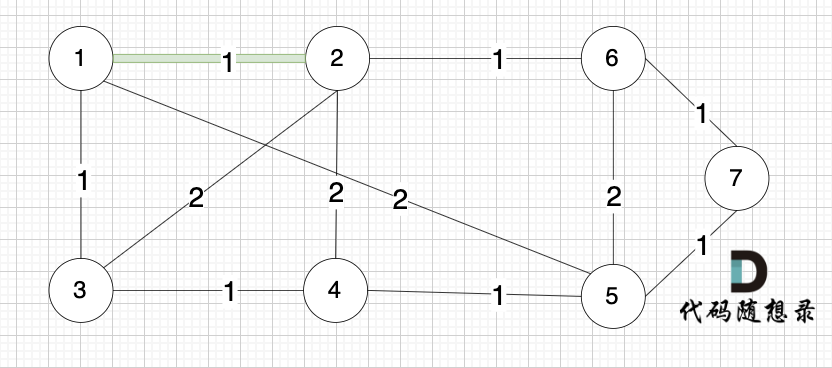
开始从头遍历排序后的边。
选边(1,2),节点1 和 节点2 不在同一个集合,所以生成树可以添加边(1,2),并将 节点1,节点2 放在同一个集合。
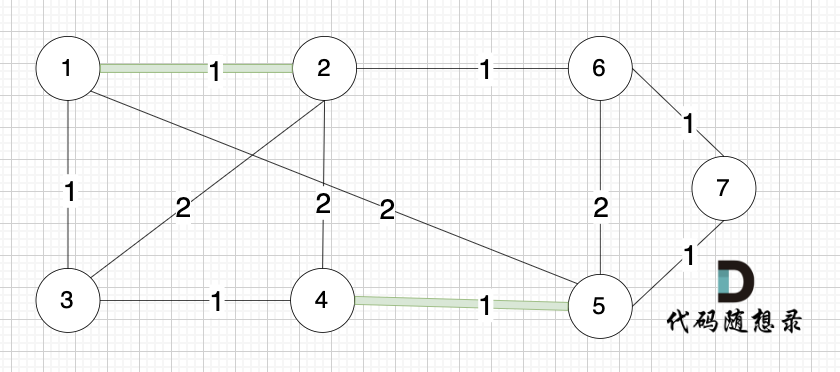
选边(4,5),节点4 和 节点 5 不在同一个集合,生成树可以添加边(4,5) ,并将节点4,节点5 放到同一个集合。
大家判断两个节点是否在同一个集合,就看图中两个节点是否有绿色的粗线连着就行
(这里在强调一下,以下选边是按照上面排序好的边的数组来选择的)
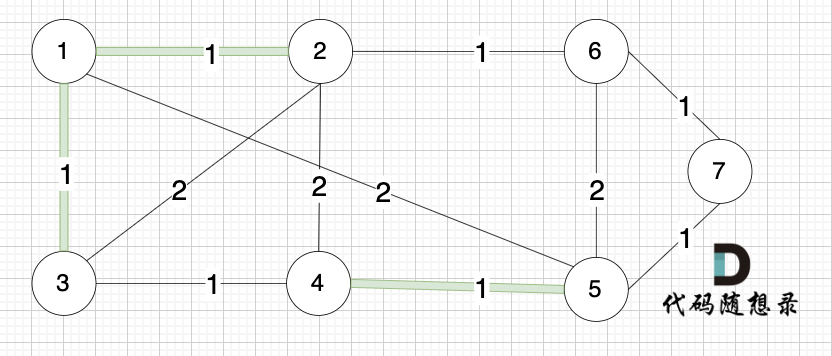
选边(1,3),节点1 和 节点3 不在同一个集合,生成树添加边(1,3),并将节点1,节点3 放到同一个集合。
选边(2,6),节点2 和 节点6 不在同一个集合,生成树添加边(2,6),并将节点2,节点6 放到同一个集合。
选边(3,4),节点3 和 节点4 不在同一个集合,生成树添加边(3,4),并将节点3,节点4 放到同一个集合。
选边(6,7),节点6 和 节点7 不在同一个集合,生成树添加边(6,7),并将 节点6,节点7 放到同一个集合。
选边(5,7),节点5 和 节点7 在同一个集合,不做计算。
选边(1,5),两个节点在同一个集合,不做计算。
后面遍历 边(3,2),(2,4),(5,6) 同理,都因两个节点已经在同一集合,不做计算。
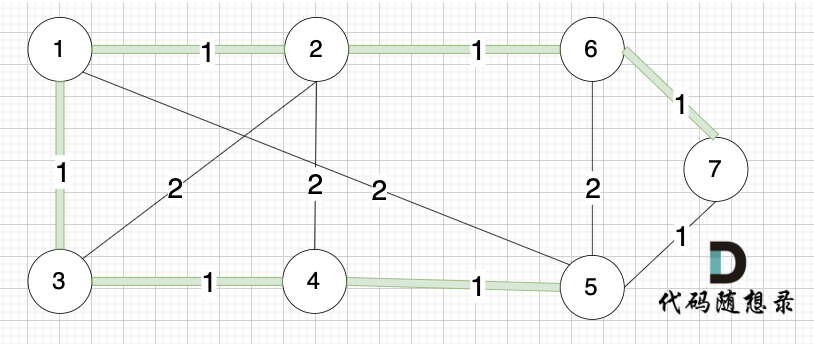
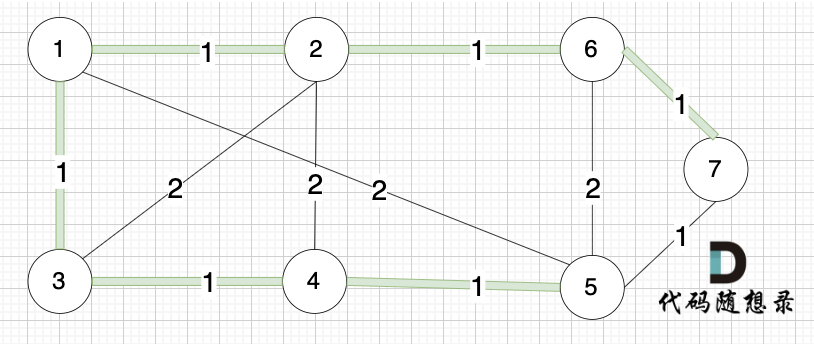
此时 我们就已经生成了一个最小生成树,即:
在上面的讲解中,看图的话 大家知道如何判断 两个节点 是否在同一个集合(是否有绿色的线连在一起),以及如何把两个节点加入集合(就在图中把两个节点连上)
但在代码中,如果将两个节点加入同一个集合,又如何判断两个节点是否在同一个集合呢?
这里就涉及到我们之前讲解的并查集。
我们在并查集开篇的时候就讲了,并查集主要就两个功能:
- 将两个元素添加到一个集合中
- 判断两个元素在不在同一个集合
大家发现这正好符合 Kruskal算法的需求,这也是为什么 我要先讲并查集,再讲 Kruskal。
思路
#include <stdio.h>
#include <stdlib.h>// 定义边结构
struct Edge {int l, r, val;
};// 比较函数,用于qsort排序
int compare(const void *a, const void *b) {return ((struct Edge*)a)->val - ((struct Edge*)b)->val;
}// 节点数量
#define MAXN 10001
// 并查集标记节点关系的数组
int father[MAXN];// 并查集初始化
void init() {for (int i = 0; i < MAXN; ++i) {father[i] = i;}
}// 并查集的查找操作
int find(int u) {if (u == father[u]) return u;else return father[u] = find(father[u]); // 路径压缩
}// 并查集的加入集合
void join(int u, int v) {u = find(u); // 寻找u的根v = find(v); // 寻找v的根if (u == v) return; // 如果发现根相同,则说明在一个集合,不用两个节点相连直接返回father[v] = u;
}int main() {int v, e;int v1, v2, val;struct Edge edges[MAXN];int edge_count = 0;int result_val = 0;// 输入节点和边数scanf("%d %d", &v, &e);// 读取边信息while (e--) {scanf("%d %d %d", &v1, &v2, &val);edges[edge_count++] = (struct Edge){v1, v2, val};}// 执行Kruskal算法// 按边的权值对边进行从小到大排序qsort(edges, edge_count, sizeof(struct Edge), compare);// 并查集初始化init();// 从头开始遍历边for (int i = 0; i < edge_count; ++i) {struct Edge edge = edges[i];// 并查集,搜出两个节点的祖先int x = find(edge.l);int y = find(edge.r);// 如果祖先不同,则不在同一个集合if (x != y) {result_val += edge.val; // 这条边可以作为生成树的边join(x, y); // 两个节点加入到同一个集合}}printf("%d\n", result_val);return 0;
}学习反思
实现了Kruskal算法,用于求解最小生成树。首先定义了边的结构体Edge,包括边的两个节点和权值。然后定义了一个比较函数compare,用于对边按权值进行排序。接着定义了并查集相关的操作,包括初始化init、查找操作find和加入集合操作join。
在主函数中,首先输入节点数和边数,然后读取边的信息。接下来执行Kruskal算法,首先对边按权值排序,然后从小到大遍历每一条边。对于每一条边,使用并查集查找出边的两个节点的祖先,如果祖先不同,则说明这条边可以加入生成树中,更新结果值并将两个节点加入同一个集合。最后输出结果。
通过使用并查集,可以快速判断两个节点是否在同一个集合中,从而判断是否形成环,保证生成树的不环路性质。Kruskal算法的时间复杂度为O(ElogE),其中E为边的数量。