引言

这是中科大最优化理论的笔记，中科大凌青老师的凸优化课程，详尽易懂，基础扎实。不论是初学者还是从业多年的人，都值得系统地好好学一遍。

本文介绍种重要的凸集:超平面与半空间、球和椭球、多面体、单纯形。

超平面与半空间

超平面是具有下面形式的集合
{ x ∣ a T x = b } (1) \{x|a^Tx=b\} \tag 1 {x∣aTx=b}(1)
其中$a\in R^n,a\ne 0,b\in R$。

$a^{T}x$是内积，$x\in R^n$。如果是二维的，那么$a^{T}x$就是直线，如果是三维的，就是平面。

假设$x_0$是超平面上的任意一点，即任意满足$a^T{x}_0=b$的点，那么式$(1)$可以表示为
{ x ∣ a T ( x − x 0 ) = 0 } (2) \{x|a^T(x-x_0) =0 \} \tag 2 {x∣aT(x−x0​)=0}(2)
内积为零，说明$a^T$与$x-x_0$正交(垂直)，假设在二维空间中：

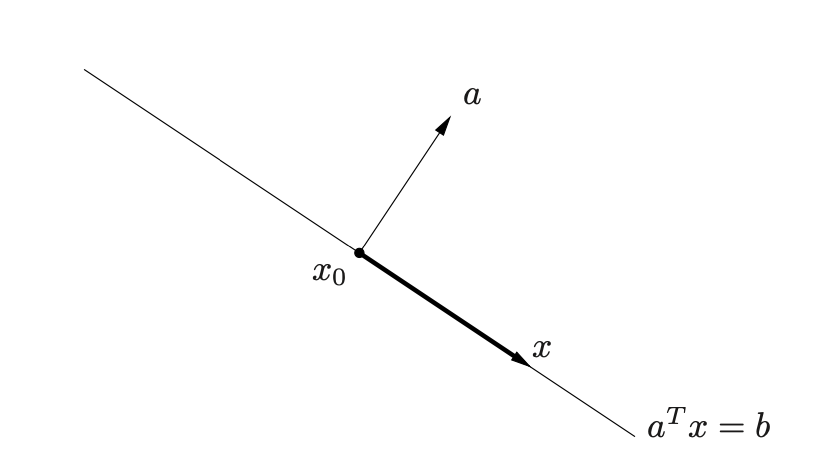
$x_0$是超平面上一点，对于超平面上任意一点$x$，$x-x_0$如上图黑色向量所示，与向量$a$正交。

这是二维空间，如果是三维空间，那么该超平面就是一个(真的)平面：

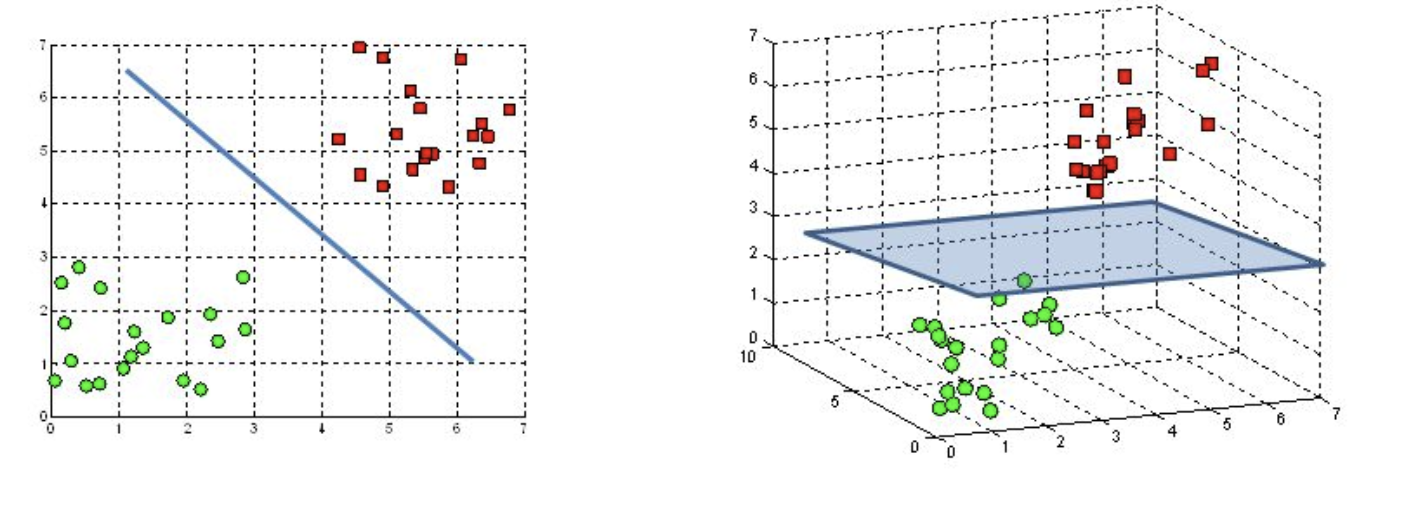
上图左侧是二维空间中的超平面(直线)，右侧是三维空间中的超平面(平面)。

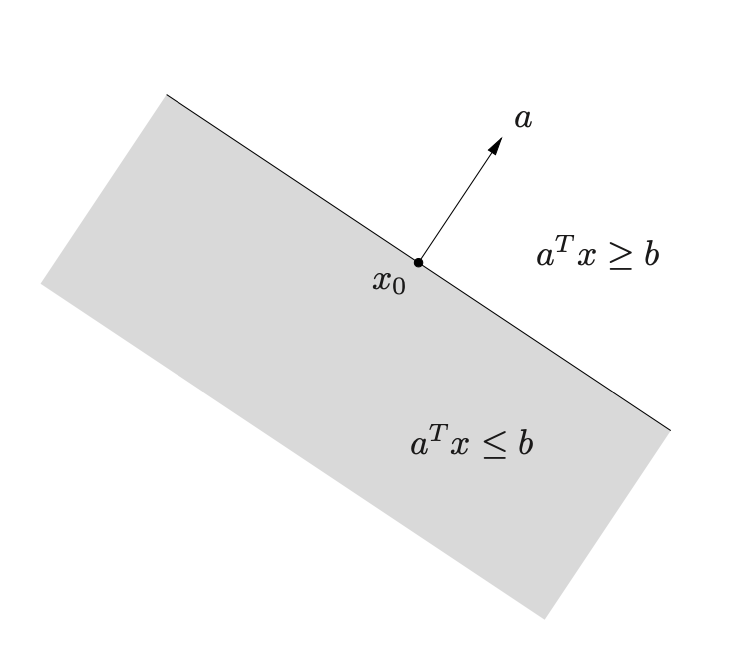
$R^2$上由$a^{T}x=b$定义的超平面决定了两个半空间。由$a^{T}x\ge b$决定的半空间(无阴影)是向$a$扩展的半空间；由$a^T\le b$确定的半空间(阴影部分)向$-a$方向扩展。

我们来看下超平面是仿射集吗？显然它是仿射集，因为它的定义就是一条直线，所以也是凸集。

那是否为凸锥呢？只有该直线过原点才是凸锥($a^{T}x=0$)。

那半空间是凸集吗？肯定是凸集，空间内任意两点构成的线段一定在半空间内。它不是仿射集，因为集合两点构成的直线有可能有另外一部分超出了该集合。只有当半空间经过原点是才有可能是凸锥。

球和椭球

$R^n$中的空间Euclid球具有下面的形式
B ( x c , r ) = { x ∣ ∣ ∣ x − x c ∣ ∣ 2 ≤ r } = { x ∣ ( x − x c ) T ( x − x c ) ≤ r } (3) B(x_c,r) = \{x| \,\, ||x-x_c||_2 \leq r\} = \{ x|\,\, \sqrt{(x-x_c)^T(x-x_c)} \leq r\} \tag 3 B(xc​,r)={x∣∣∣x−xc​∣∣2​≤r}={x∣(x−xc​)T(x−xc​) ​≤r}(3)
其中$x_c\in R$是球心，标量$r>0$为半径。$B(x_c,r)$由距离球心$x_c$不超过$r$的所有点组成。

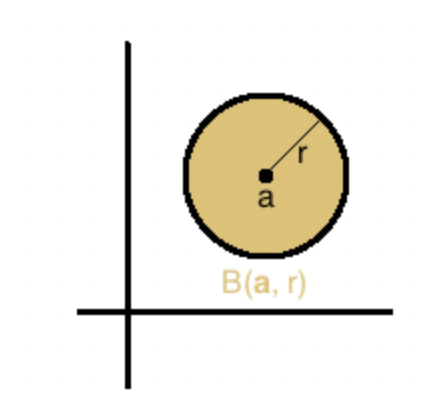
在二维空间中的球就是一个圆，它显然是凸集。那么是否为仿射集呢？只有当半径为零，坍塌为一个点是才是仿射集。同时该点落在原点上才是凸锥。

我们能很容易看出来该集合是一个凸集，那如何用公式证明呢？

$\forall x_1,x_2\in B$，即有 $||x_1-x_c|{|}_2\le r,||x_2-x_c|{|}_2\le r$, $\forall \theta ,1\ge \theta \ge 0$，那么我们要证明连接这两点的线段也在集合内，有：
$$\begin{array}{rl}||\theta x_1+(1-\theta )x_2-x_c|{|}_2& =||\theta (x_1-x_c)+(1-\theta )(x_2-x_c)|{|}_2\\ & \le ||\theta (x_1-x_c)|{|}_2+||(1-\theta )(x_2-x_c)|{|}_2\\ & =\theta ||x_1-x_c|{|}_2+(1-\theta )||x_2-x_c|{|}_2\\ & \le r\end{array}$$
其中利用了三角不等式$||a+b||\le ||a||+||b||$。

另一个相关的凸集是椭球，它们具有如下形式，
ε = { x ∣ ( x − x c ) T P − 1 ( x − x c ) ≤ 1 } (4) \varepsilon =\{ x|(x-x_c)^TP^{-1}(x-x_c) \leq 1 \} \tag 4 ε={x∣(x−xc​)TP−1(x−xc​)≤1}(4)
其中$x_c\in R^n$，$P\in S_{++}^n$，即$P$是对称正定矩阵。

一个对称矩阵为正定的，当且仅当其所有的特征值均为正的。

矩阵$P$决定了椭球从$x_c$向各个方向扩展的幅度。$\epsilon$的半轴长度由$\sqrt{{\lambda }_i}$给出，这里${\lambda }_i$为$P$的特征值。

球可以看成是$P=r^{2}I$的椭球。

下面是一个椭球在二维空间中的例子：

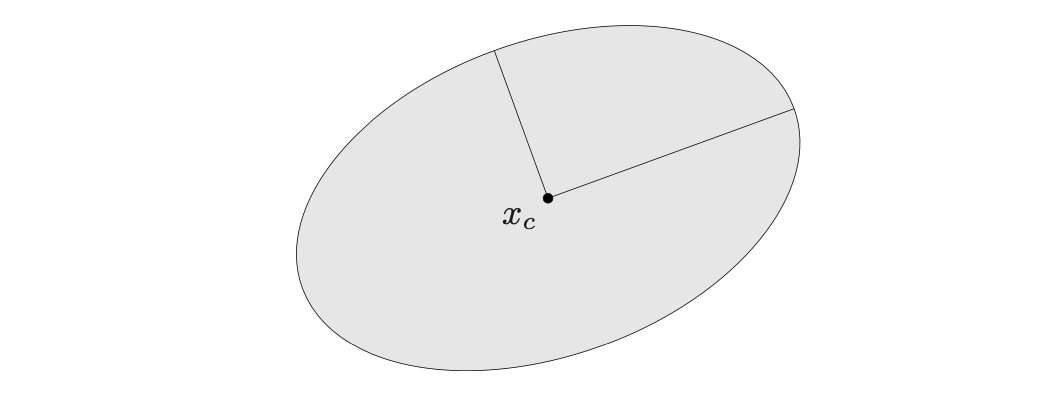
中心$x_c$在上图的实心点，两个半轴由线段表示。

公式$(4)$不太好理解，这和我们以前学的椭球的定义不太一样。我们就通过一个例子来理解。

假设在$R^2$中
$$P=\left[\begin{array}{cc}4& 0\\ 0& 1\end{array}\right]$$
首先求它的特征值，特征方程为
$$\left|\begin{array}{cc}4-\lambda & 0\\ 0& 1-\lambda \end{array}\right|=0\Rightarrow (4-\lambda )(1-\lambda )=0$$
即$P$的特征值为$4$或$1$都大于零。因此它是正定的，且又是对称的。

同时假设椭球的球心在原点处，$x=(x_1,x_2{)}^T$，有
$$\begin{gathered} x^T{P}^{-1}x=\left[\begin{array}{cc}{x}_1& x_2\end{array}\right]{\left[\begin{array}{cc}4& 0\\ 0& 1\end{array}\right]}^{-1}\left[\begin{array}{c}{x}_1\\ x_2\end{array}\right] \\ =\left[\begin{array}{cc}\frac{1}{4}{x}_1& x_2\end{array}\right]\left[\begin{array}{c}{x}_1\\ x_2\end{array}\right] \\ =\frac{1}{4}{x}_1^2+x_2^2 \end{gathered}$$
即$\{(x_1,x_2)|\frac{1}{4}{x}_1^2+x_2^2\le 1\}$是长轴为$2$，短轴为$1$的椭圆。

多面体

多面体(Polyhedra)被定义为有限个线性等式和不等式的解集(集合)：
P = { x ∣ a j T x ≤ b j , j = 1 , ⋯ , m , c j T x = d j , j = 1 , ⋯ , p } (5) \mathcal P = \{x| a_j^Tx \leq b_j,\, j=1,\cdots,m, \quad c_j^Tx=d_j,\, j =1,\cdots,p\} \tag{5} P={x∣ajT​x≤bj​,j=1,⋯,m,cjT​x=dj​,j=1,⋯,p}(5)
不等式表达的是半空间；等式表达式超平面。所以多面体实际上是一些半空间和一些超平面的交集。

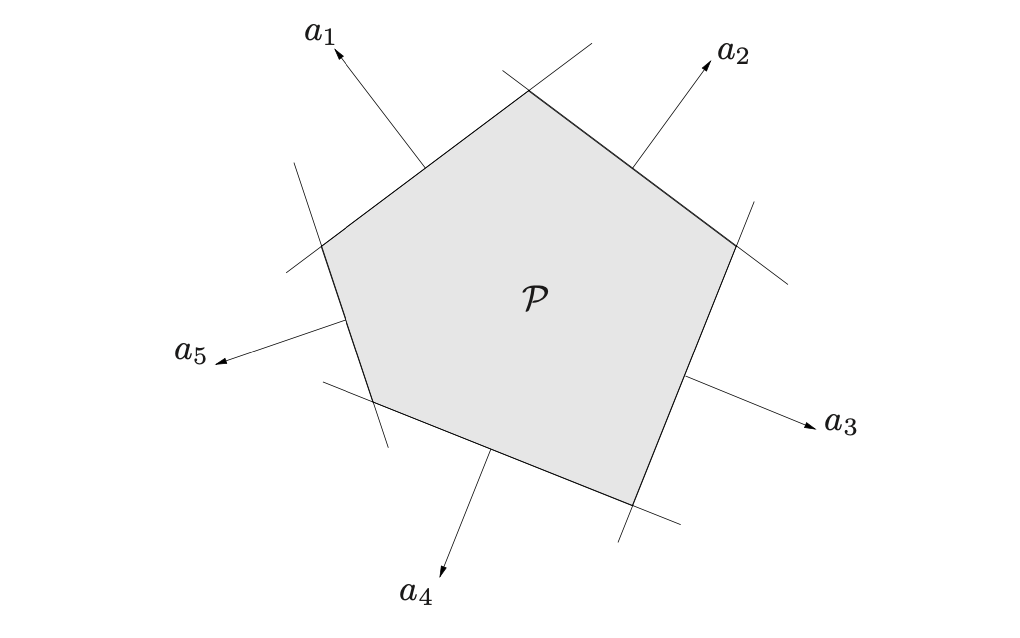
上面是由五个半空间的交集定义的多面体。

但要注意，多面体不一定是有界的，只有一个半空间约束的也叫多面体。

如果是有界的就称为有界多面体，多面体是凸集。

单纯形

单纯形(Simplex)是一种特殊的多面体。

在$R^n$空间中选择$v_0,\cdots ,v_k$共$k+1$个点，$v_1-v_0,\cdots ,v_k-v_0$线性无关，则与上述点相关的单纯形为：
C = conv { v 0 , ⋯ , v k } = { θ 0 v 0 + ⋯ + θ k v k , θ ≥ 0 , 1 T θ = 1 } (6) C=\text{conv} \{v_0,\cdots,v_k\} = \{\theta_0v_0 +\cdots + \theta_kv_k,\theta \ge 0,\pmb 1^T\theta = 1\} \tag{6} C=conv{v0​,⋯,vk​}={θ0​v0​+⋯+θk​vk​,θ≥0,1Tθ=1}(6)
显然这是一个凸包，其中$\theta$向量的每个分量都大于零，且$\theta$各分量之和等于1。

这个单纯形的仿射维数为$k$，因此也称为$R^n$空间的$k$维单纯形。

一些常见的单纯形： 1维单纯形是一条线段；2维单纯形是一个三角形(包含其内部)；3维单纯形是一个四面体。

我们来看二维空间单纯形的例子。

在二维空间中选择$k=1$，即选择两个点：$v_0,v_1$。

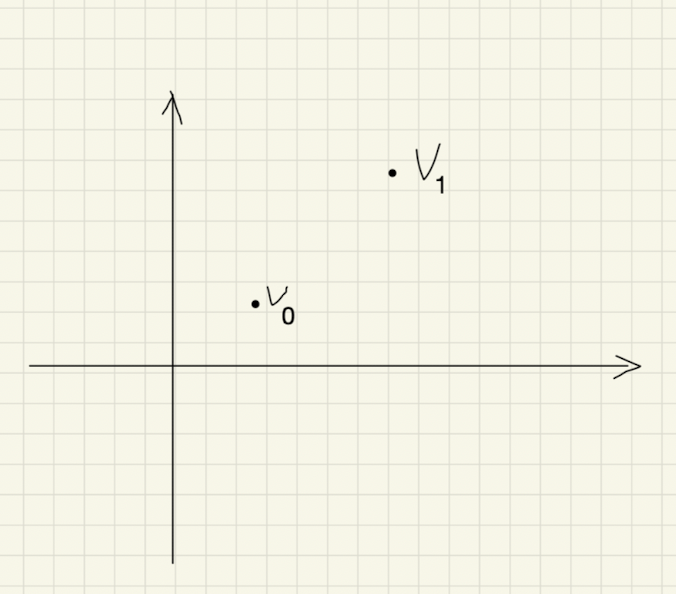
那么$v_1-v_0$是否是线性无关的，显然只要这个向量不等于零，它就是线性无关的。由这两点所构造的单纯形是一个线段。

如果把$k$加1，即令$k=2$，那么此时就有两个向量了：

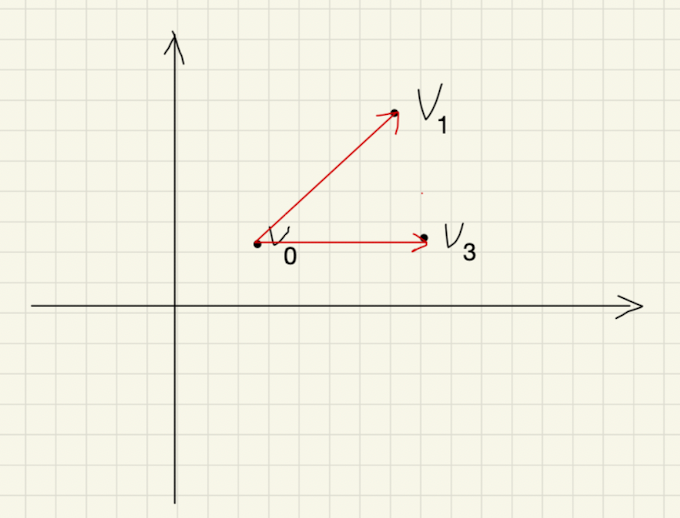
此时所对应的单纯形就是包含内部的三角形：

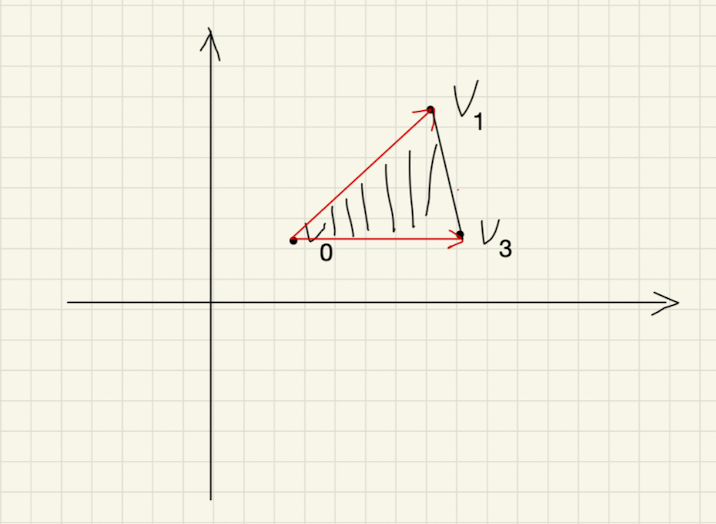
如果再让$k+1=3$，那么无法在二维空间中构成单纯形，因为二维空间只需要两个向量就能确定，三个向量一定不是线性无关的。

证明： 单纯形是多面体的一种

解： 首先基于单纯的定义

$x\in C\in R^n$，$C$为单纯形 $\iff$ $x={\theta }_0{v}_0+\cdots +{\theta }_k{v}_k,\theta \ge 0,1^T\theta =1$，$v_1-v_0,\cdots ,v_k-v_0$线性无关。

定义一个新的向量和矩阵：
$$\begin{gathered} [{\theta }_1\cdots {\theta }_k{]}^T=yy\ge 01^{T}y\le 1 \\ [v_1-v_0,\cdots ,v_k-v_0]=B\in R^{k\times k} \end{gathered}$$
注意这个向量去掉了${\theta }_0$，所以$1^{T}y\le 1$。

然后把$x$拆开
$$\begin{array}{rl}x\in C\iff x& ={\theta }_0{v}_0+\cdots +{\theta }_k{v}_k\\ & =v_0-v_0(1-{\theta }_0)+{\theta }_1{v}_1+\cdots +{\theta }_k{v}_k\\ & =v_0-v_0({\theta }_1+{\theta }_2+\cdots +{\theta }_k)+{\theta }_1{v}_1+\cdots +{\theta }_k{v}_k\\ & =v_0+{\theta }_1(v_1-v_0)+\cdots +{\theta }_k(v_k-v_0)\\ & =v_0+By\end{array}\text{\hspace{1em}(7)}$$
因为$B$中的$k$个向量是线性无关的，所以$rank(B)=k,k\le n$，说明$B$是一个列满秩矩阵。

所以可以把$B$变成一个
$$\left[\begin{array}{c}{I}_k\\ 0\end{array}\right]$$
上面是一个$k\times k$的单位阵，下面是一个$(n-k)\times k$的零矩阵。

即存在非奇异矩阵
$$A={\left[\begin{array}{c}{A}_1\\ A_2\end{array}\right]}_{n\times n}$$
可以使得
$$AB=\left[\begin{array}{c}{A}_1\\ A_2\end{array}\right]B=\left[\begin{array}{c}{I}_k\\ 0\end{array}\right]$$
把$(7)$式两边左乘这样一个$A$有：
$$\begin{array}{rl}& Ax=A{v}_0+ABy\\ & \iff \left[\begin{array}{c}{A}_1\\ A_2\end{array}\right]v_0+\left[\begin{array}{c}{A}_{1}B\\ A_{2}B\end{array}\right]y\\ & \iff \{\begin{array}{l}{A}_{1}x=A_1{v}_0+y\\ A_{2}x=A_2{v}_0\end{array}\\ & \iff \{\begin{array}{ll}{A}_{1}x\ge A_1{v}_0& \\ 1^T{A}_{1}x\le 1+1^T{A}_1{v}_0& 利用y的性质得到这两个不等式\\ A_{2}x=A_2{v}_0& \end{array}\end{array}$$
这里说的$y$的性质是指$y\ge 01^{T}y\le 1$。

如果改变$y$就可以得到单纯形中所有的点，即单纯形中任意的$x$都可以由上面包含不等式的三个式子描述。

所以说任何的单纯形都是一个多面体(等式和不等式约束)。

一些矩阵集合

记对称矩阵集合 S n = { x ∈ R n × n ∣ x = x T } S^n = \{x \in R^{n \times n} | x=x^T\} Sn={x∈Rn×n∣x=xT}

记对称半正定矩阵集合 S + n = { x ∈ R n × n ∣ x = x T , x ≽ 0 } S^n_+ = \{x \in R^{n \times n} | x=x^T, x ≽ 0\} S+n​={x∈Rn×n∣x=xT,x≽0}

其中，$ x ≽ 0$表示$x$的所有奇异值都是大于等于零的。

记对称正定矩阵集合 S + + n = { x ∈ R n × n ∣ x = x T , x ≻ 0 } S_{++}^n = \{x \in R^{n \times n} | x=x^T, x ≻ 0\} S++n​={x∈Rn×n∣x=xT,x≻0}

那这三个集合是不是凸集？

我们先来看集合$S_{+}^n$有什么性质。

回顾下凸锥的定义，集合$C$是凸锥(Convex cone) 等价于对于任意$x_1,x_2\in C$和${\theta }_1,{\theta }_2\ge 0$都有${\theta }_1{x}_1+{\theta }_2{x}_2\in C$。

证明： $S_{+}^n$是凸锥

$\forall {\theta }_1\ge 0,{\theta }_2\ge 0\forall A,B\in S_{+}^n$证明凸锥组合${\theta }_{1}A+{\theta }_{2}B\in S_{+}^n$。

对称很好证明，如果$A,B$都是对称矩阵，那么它们的凸锥组合也一定是对称矩阵。

如何证明半正定呢？如何矩阵$A$或$B$是半正定矩阵的话，那么对于任意的$X$有：

$\forall x\in R^n{x}^{T}Ax\ge 0x^{T}Bx\ge 0$

其中$ x^TAx, x^TBx$都是标量。

下面我们要证明这里的凸锥组合也满足这个性质，即
$$x^T({\theta }_{1}A+{\theta }_{2}B)x=x^T{\theta }_{1}Ax+x^T\theta Bx\ge 0$$
证明完毕。

如果$A,B$都是对称矩阵，那么它们的凸锥组合也一定是对称矩阵，所以对称的矩阵集合也是一个凸锥。

那对称的正定矩阵集合是不是凸锥呢？

考虑最简单的情况，假设维度$n=1$，$S_{+}^n=R_{+}$，即变成了一个非负的实数空间。

首先标量的转置是等于本身的，其次这个标量值要大于等于零的。

对应的$S_{++}^n=R_{++}$，即一个正实数集合，那么显然不是凸锥，因为它不包括原点(零)，但是它是一个凸集。

$S^n=R$就是一个实数了。