Masked Spatial Propagation Network for Sparsity-Adaptive Depth Refinement （CVPR 2024）

用于稀疏自适应深度细化的掩码空间传播网络

论文地址：CVPR官网 arxiv

项目链接：github地址

摘要：深度补全的主要功能是弥补硬件传感器提供的稀疏深度测量点数量不足且不可预测的问题。然而，现有的深度补全研究假设稀疏性（即点数或 LiDAR 线数）在训练和测试过程中是固定的。因此，当稀疏深度的数量发生显著变化时，补全性能会大幅下降。为了解决这一问题，我们提出了稀疏自适应深度细化（SDR）框架，该框架使用稀疏深度点来优化单目深度估计。针对SDR，我们提出了掩码空间传播网络（MSPN），它能够通过逐步传播稀疏深度信息至整个深度图，有效地处理不同数量的稀疏深度点。实验结果表明，MSPN在SDR和传统深度补全场景中都达到了当前最先进的性能表现。

1 介绍

图像引导的深度补全是一项通过利用稀疏深度测量和RGB图像来估计密集深度图的任务；它通过估算深度来填充未测量的区域。由于许多深度传感器（如LiDAR和飞行时间相机（ToF））只能提供稀疏的深度图，这项任务变得尤为重要。随着深度信息在自动驾驶和各种3D应用中的广泛应用，深度补全已经成为一个重要的研究课题。

近年来，随着深度神经网络的成功，基于学习的方法通过利用大量训练数据显著提升了性能。这些方法尝试融合多模态特征，如表面法线或提供重复的图像引导。尤其是，基于亲和性的空间传播方法被广泛研究。

深度补全的主要功能是弥补现有深度传感器的局限性，但传统的深度补全研究通常假设稀疏性在训练和测试中是固定的。然而，实际上稀疏性会显著变化，因为在透明区域、镜子以及黑色物体上很难测量到深度。此外，传感器缺陷也会影响测量的数量。传统的空间传播方法在深度细化时通常对所有像素进行同时处理，而不考虑稀疏深度测量点的位置。因此，当只有少量稀疏深度点可用时，错误的深度信息可能会在细化过程中传播。

在本文中，我们提出了一个稀疏自适应深度细化（SDR）框架，该框架根据深度测量的稀疏性自适应地优化单目密集深度估计。此外，我们提出了掩码空间传播网络（MSPN），用于将稀疏深度点的信息传播到未测量的区域。首先，我们使用现成的单目深度估计器从输入的RGB图像中估计一个初始深度图。接下来，一个引导网络使用输入图像、稀疏深度和初始深度图生成引导特征。最后，利用这些引导特征，所提出的 MSPN 通过迭代细化生成一个优化的深度图，如图1所示。

所提出的SDR框架能够在不同数量的稀疏深度点下进行训练，使其更加适用于实际应用。此外，所提出的MSPN通过根据稀疏测量生成自适应传播掩码，在 SDR 场景中比传统方法表现显著更好。此外，MSPN 在 NYUv2 和 KITTI 数据集上的传统深度补全任务中也提供了最先进的性能表现。

本文的贡献如下：

• 我们开发了 SDR 框架，该框架利用可变数量的稀疏深度测量点来优化单目深度估计。
• 针对 SDR，我们提出了 MSPN，以逐步传播稀疏深度信息，从而处理不同数量的稀疏深度点。
• MSPN 在 SDR 和传统深度补全场景中均提供了最先进的性能表现。

2 算法流程

网络架构" />

2.1 问题建模

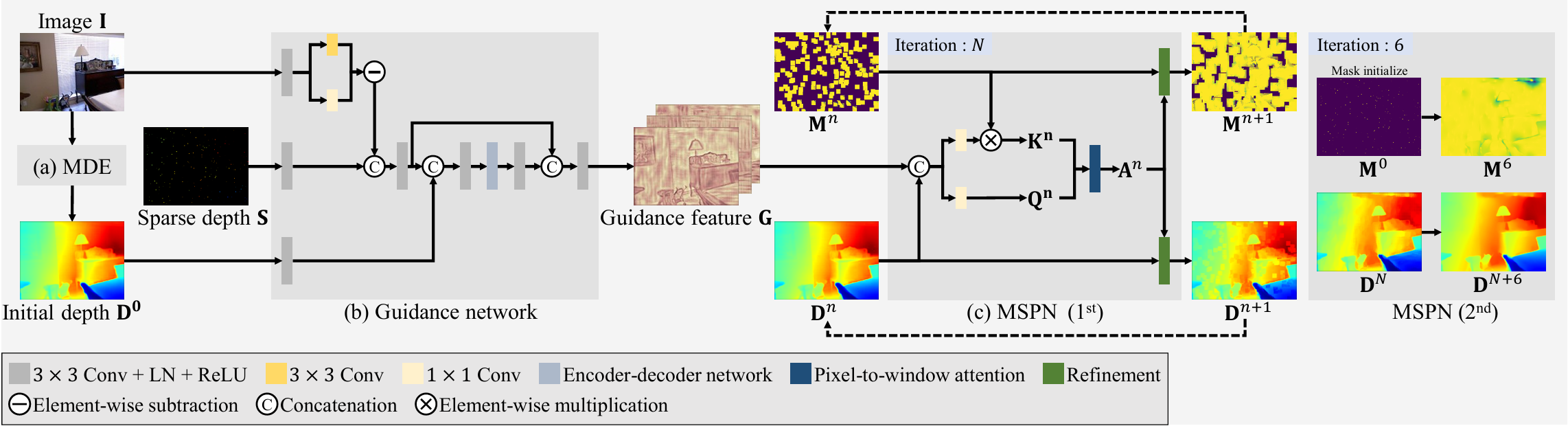
如上图2所示本文提出的模型输入为 图像 $\mathbf{I}\in {\mathbb{R}}^{3\times H\times W}$ 和稀疏深度图$\mathbf{S}\in {\mathbb{R}}^{H\times W}$ ，最终输出为密集深度图$\mathbf{D}\in {\mathbb{R}}^{H\times W}$。

该模型总共分为三部分包括：

• 用于预测初始深度 ${\mathbf{D}}^0\in {\mathbb{R}}^{H\times W}$ 的单眼深度估计模型 MDE
• 用于融合不同模态的特征并生成指导特征$\mathbf{G}\in {\mathbb{R}}^{C\times H\times W}$的指导网络 Guidance network
• 用于迭代传播稀疏深度信息的 MSPN 模块

首先，RGB图像 $\mathbf{I}$ 被输入到 MDE 中已得到初步的深度图 ${\mathbf{D}}^0$ ；接着，RGB图像 $\mathbf{I}$、稀疏深度图 $\mathbf{S}$ 和初步深度图 ${\mathbf{D}}^0$ 被输入到 Guidance network 用于生成指导特征 $$\mathbf{G}$$；最后，深度图 ${\mathbf{D}}^{\mathbf{n}}$ 、 掩码 ${\mathbf{M}}^{\mathbf{n}}$ 和指导特征 $\mathbf{G}$ 被输入到 MSPN 模块多次迭代逐步输出更精细的深度图。其中，$\mathbf{M^0}=\Xi\left ( \mathbf{S}\right ) $ ，$\Xi$表示指示函数，对于每个稀疏深度点输出 1，否则输出 0。（MDE模型采用了论文提供的预训练模型）

2.2 Guidance Network

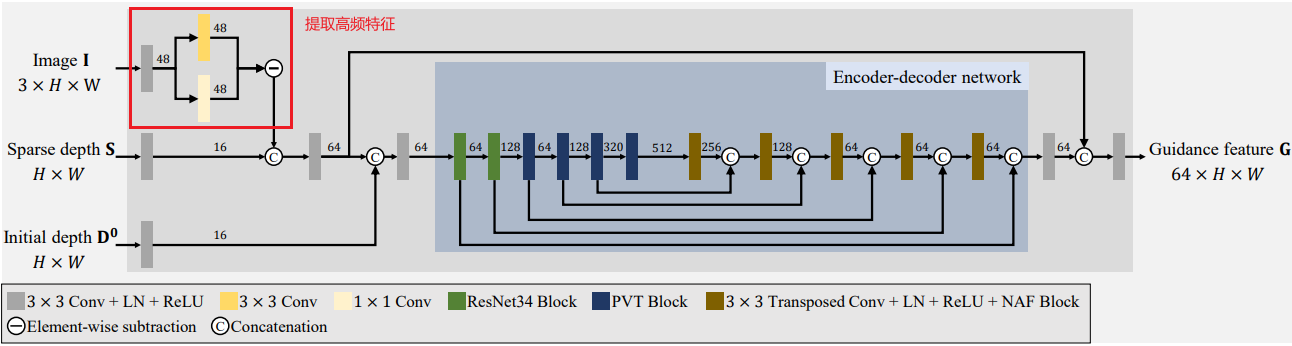
Guidance Network 中，输入信号 $\mathbf{I}$ 、$\mathbf{S}$ 和 ${\mathbf{D}}^0$ 分别生成 48、16 和 16 个通道的特征，这些特征通过拼接和卷积进行混合。混合后的特征被送入一个编码器-解码器网络。作为编码器，我们采用 PVT-Base，它处理一个 64 × H × W的张量，输出大小为 512 × H/32 × W/32 的编码特征。解码器由五个模块组成，每个模块执行 3 × 3 转置卷积、层归一化、ReLU 激活函数和 NAF 模块操作。每个解码器模块中的通道数保持不变。

提取高频特征

如红框中所示，通过从3×3卷积结果中减去1×1卷积结果来提取高频特征，类似于论文中的方法。

2.3 MSPN 模块

MSPN 的输入为 ${\mathbf{D}}^{\mathbf{n}}$ 和 ${\mathbf{M}}^{\mathbf{n}}$ 输出 ${\mathbf{D}}^{\mathbf{n}+1}$ 和 ${\mathbf{M}}^{\mathbf{n}+1}$ ，不断迭代并细化深度图。首先，使用 $\mathbf{S}$ 替换 ${\mathbf{D}}^{\mathbf{n}}$ 中的深度值得到 ${\tilde{\mathbf{D}}}^{\mathbf{n}}$ ，公式如下：
$${\tilde{\mathbf{D}}}^{\mathbf{n}}=(1-{\mathbf{M}}^0)\otimes {\mathbf{D}}^{\mathbf{n}}+{\mathbf{M}}^0\otimes \mathbf{S}$$
其中，$\otimes $ 代表元素乘法。接着，确定细化过程中的参考像素和细化的强度。传统的空间传播方法集中于选择参考像素。然而，可靠的像素远少于不可靠的像素，因此当仅提供少量稀疏深度时，这些方法的效果较差。为此，我们设计了基于掩码注意力的动态滤波器，该滤波器计算每个像素与其周围像素之间的注意力得分。

首先，分别生成 查询特征 $\mathbf{Q}\in {\mathbb{R}}^{L\times H\times W}$ 和键特征 $\mathbf{K}\in {\mathbb{R}}^{L\times H\times W}$：
$${\mathbf{Q}}^{\mathbf{n}}=f_{\mathbf{Q}}([{\tilde{\mathbf{D}}}^{\mathbf{n}},\mathbf{G}]),{\mathbf{K}}^{\mathbf{n}}=f_{\mathbf{K}}([{\tilde{\mathbf{D}}}^{\mathbf{n}},\mathbf{G}])\otimes {\mathbf{M}}^{\mathbf{n}}$$
其中，$f_{\mathbf{Q}}$ 和 $f_{\mathbf{K}}$ 都由一个 1×1 的卷积层和 LN层组成；$[\cdot ]$ 代表通道维度拼接。由于 ${\tilde{\mathbf{D}}}^{\mathbf{n}}$ 尚未细化，所以，${\mathbf{K}}^{\mathbf{n}}$是可靠和不可靠像素特征的混合。因此，在计算 ${\mathbf{K}}^{\mathbf{n}}$ 时，我们会对不可靠的像素特征进行掩码处理。也就是公式中最后需要把 $$f_{\mathbf{K}}$$ 的结果与 ${\mathbf{M}}^{\mathbf{n}}$ 进行元素乘法。

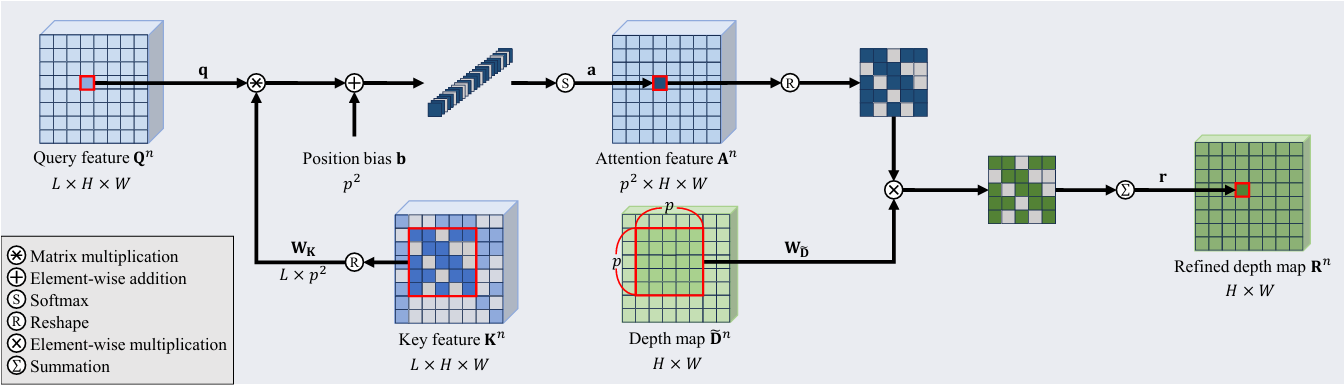
接着，接下来，我们计算 ${\mathbf{Q}}^{\mathbf{n}}$ 和 $\mathbf{K^n} $ 之间的注意力得分。设 $\mathbf{q}\in {\mathbb{R}}^L$ 为 $\mathbf{Q^n} $ 中位于位置 $(i,j)$ 的查询像素特征。同时，设 ${\mathbf{W}}_{\mathbf{k}}\in {\mathbb{R}}^{L\times p^2}$ 表示 $\mathbf{K^n} $ 中以 $(i,j)$ 为中心的 $p\times p$ 窗口内的键特征。请注意，我们计算的是像素到窗口的注意力，以使用其邻近像素来细化像素 $(i,j)$。更具体地说，像素到窗口的注意力 $\mathbf{a}\in {\mathbb{R}}^{p^2}$ 计算如下：
$$\mathbf{a}=\text{softmax}({\mathbf{q}}^{\mathbf{T}}{\mathbf{W}}_{\mathbf{K}}+\mathbf{b})$$
其中，$\mathbf{b}\in {\mathbb{R}}^{p^2}$ 代表 $w\times w$ 窗口中的相对位置偏置，通过对 $\mathbf{Q^n} $ 的所有像素执行注意力操作，获得注意力特征 ${\mathbf{A}}^{\mathbf{n}}\in {\mathbb{R}}^{p^2\times H\times W}$。

然后，使用 ${\mathbf{A}}^{\mathbf{n}}$ 和 ${\tilde{\mathbf{D}}}^{\mathbf{n}}$，我们生成了一个精细化的深度图 ${\mathbf{R}}^{\mathbf{n}}\in {\mathbb{R}}^{\times H\times W}$。令 KaTeX parse error: Got function '\tilde' with no arguments as subscript at position 11: \mathbf{W_\̲t̲i̲l̲d̲e̲{D}} 和 ${\mathbf{W}}_{\mathbf{M}}$ 分别表示 ${\tilde{\mathbf{D}}}^{\mathbf{n}}$ 和 ${\mathbf{M}}^{\mathbf{n}}$ 中以 $(i,j)$ 为中心的 $p\times p$ 窗口。精细化后的深度像素 $\mathbf{r}$ 在 ${\mathbf{R}}^{\mathbf{n}}$ 中的计算方式为：
$$\mathbf{r}=\sum _{t=1}^{p^2}{\mathbf{a}}_t\cdot {\mathbf{W}}_{\tilde{\mathbf{D}},t}$$
$t$ 代表窗口中的第 $t$ 个元素。图4展示了 pixel-to-window 注意力机制的处理过程。

最后，深度图 ${\mathbf{D}}^{\mathbf{n}+1}$ 和掩码 ${\mathbf{D}}^{\mathbf{n}+1}$ 分别由下面的两个公式生成：
$${\mathbf{D}}^{n+1}=(1-{\mathbf{M}}^n)\otimes {\tilde{\mathbf{D}}}^n+{\mathbf{M}}_n\otimes {\mathbf{R}}_n$$

$${\mathbf{m}}_{n+1}=\sum _{t=1}^{p^2}{\mathbf{a}}_t\cdot W_{\mathbf{M},t}$$

3 实验结果

3.1 稀疏度自适应深度细化对比试验

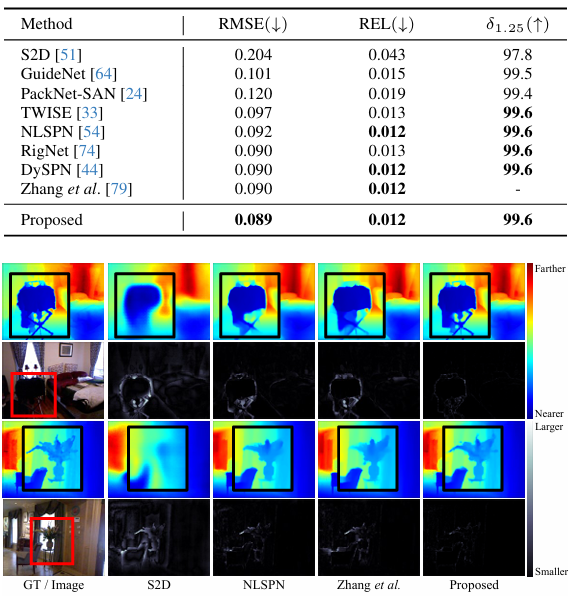
在图 5 和图 6 中，实线表示单个模型在不同稀疏深度数量下的评估结果；相反，每个符号表示为固定数量的稀疏深度分别训练并评估的模型。我们可以从图 5 和图 6 中得出以下结论：

• 通过比较图 5 中的实线，可以看出，所提出的 MSPN 在 NYUv2 数据集上的所有稀疏深度数量下都优于其他方法。
• 具体而言，一些方法专门针对较多的稀疏深度，随着稀疏深度的减少，它们的性能显著下降。相反，一些方法专门针对较少的稀疏深度，而当稀疏深度增加时，它们的性能仅有少量改善。
• 另一方面，MSPN 展现出与那些为特定稀疏深度训练的符号标记方法类似的性能。这表明 MSPN 在不同的稀疏深度数量下都能产生稳健的结果。
• 在图 6 中，MSPN 在 KITTI 数据集上，当稀疏深度小于 64 行时，显著优于其他方法。
• 对于 KITTI 数据集，那些专门针对某个特定激光雷达线数的方法在较少线数下表现不佳。相反，MSPN 利用单目深度估计结果，无论线数多少，都能有效进行深度补全。
• 总体而言，MSPN 比传统算法在不同稀疏深度数量下生成更可靠的深度图，这表明 MSPN 更适合真实世界的应用。

3.2 深度补全对比试验

虽然 MSPN 的主要关注点是 SDR（稀疏深度自适应精化），但我们也评估了 MSPN 在常规深度补全场景下的性能。对于这种常规深度补全，我们在引导网络中添加了另一个解码器头来预测初始深度图，并且不像之前的工作那样使用单目深度估计器。关于常规深度补全的详细网络结构见补充文档。

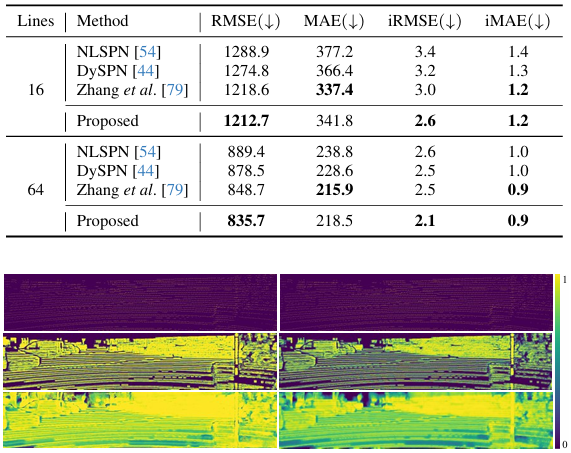
我们使用固定数量的稀疏深度来训练和测试我们的模型。对于 NYUv2 数据集，我们从真实深度中随机采样 500 个稀疏深度点，并训练网络 72 个周期。对于 KITTI 数据集，我们分别为 16 和 64 条激光雷达线条训练专门的模型，同样训练 72 个周期。为了在 KITTI 上进行公平比较，我们使用提供的 10k 子集进行训练。

下面两个表分别比较了在 NYUv2 和 KITTI 数据集上的性能。可以看到，所提出的 MSPN 在常规深度补全任务上也提供了最先进的性能。图 7 通过定性分析将结果与进行了比较，可以看出 MSPN 更有效地填充了具有挑战性的区域，并提供了更精细的细节。