用于函数优化的一维 (1D) 测试函数

news/2025/1/11 6:23:36/

         【翻译自 ： One-Dimensional (1D) Test Functions for Function Optimization】

         【说明：Jason Brownlee PhD大神的文章个人很喜欢，所以闲暇时间里会做一点翻译和学习实践的工作，这里是相应工作的实践记录，希望能帮到有需要的人！】

         函数优化是一个研究领域，它寻求函数的输入，导致函数的最大或最小输出。

        优化算法有很多，在简单易懂的测试函数上研究和开发优化算法的直觉是很重要的。

      一维函数采用单个输入值并输出对输入的单个评估。 当研究函数优化时，它们可能是最简单的测试函数类型。

      一维函数的好处是它们可以被可视化为二维图，x 轴上是函数的输入，y 轴上是函数的输出。 函数的已知最优值和函数的任何采样也可以绘制在同一图上。

      在本教程中，您将发现在学习函数优化时可以使用的标准一维函数。

 

教程概述

         我们可以使用许多不同类型的简单一维测试函数。尽管如此，在函数优化领域中还是有一些常用的标准测试函数。在测试不同的算法时，我们可能希望选择测试函数的特定属性。我们将在本教程中探索少量简单的一维测试函数，并按它们的属性将它们分为五个不同的组；他们是：

凸单峰函数
非凸单峰函数
多模态函数
不连续函数（非平滑）
嘈杂的函数

        每个函数都将使用 Python 代码呈现，其中包含目标目标函数的函数实现和函数的样本，该函数的样本显示为线图，并清楚地标记了函数的最优值。

       所有的函数都表现为一个最小化问题，例如找到导致函数最小（最小值）输出的输入。通过向所有输出添加负号，任何最大化函数都可以成为最小化函数。类似地，任何最小化函数都可以以相同的方式最大化。

        这些函数不是我发明的；它们取自文献。请参阅进一步阅读部分以获取参考资料。

       然后，您可以选择并复制粘贴一个或多个函数的代码以在您自己的项目中使用，以研究或比较优化算法的行为。

凸单峰函数

       凸函数是一种函数，其中可以在域中的任意两点之间绘制一条线，并且该线保留在域中。对于显示为二维图的一维函数，这意味着该函数具有碗状形状，并且两者之间的线保持在碗上方。单峰意味着函数有一个最优解。 凸函数可能是也可能不是单峰的； 类似地，单峰函数可能是也可能不是凸的。以下函数的范围限制为-5.0和5.0，最佳输入值为0.0。

# convex unimodal optimization function
from numpy import arange
from matplotlib import pyplot# objective function
def objective(x):return x**2.0# define range for input
r_min, r_max = -5.0, 5.0
# sample input range uniformly at 0.1 increments
inputs = arange(r_min, r_max, 0.1)
# compute targets
results = objective(inputs)
# create a line plot of input vs result
pyplot.plot(inputs, results)
# define optimal input value
x_optima = 0.0
# draw a vertical line at the optimal input
pyplot.axvline(x=x_optima, ls='--', color='red')
# show the plot
pyplot.show()

       运行示例将创建函数的折线图，并用红线标记最优值。

        这个函数可以通过添加或减去一个常数值在数轴上向前或向后移动，例如 5 + x^2。

        如果希望将最佳输入从 0.0 值移开，这会很有用。

非凸单峰函数

        如果无法在域中的两点之间绘制一条线并且该线保留在域中，则函数为非凸函数。这意味着可以在域中找到两个点，它们之间的线与函数的线图相交。通常，如果一维函数的图有多个山丘或山谷，那么我们立即知道该函数是非凸函数。 然而，非凸函数可能是也可能不是单峰的。我们对优化感兴趣的大多数实际函数都是非凸函数。以下函数的范围限制为-10.0和10.0，最佳输入值为0.67956。

# non-convex unimodal optimization function
from numpy import arange
from numpy import sin
from numpy import exp
from matplotlib import pyplot# objective function
def objective(x):return -(x + sin(x)) * exp(-x**2.0)# define range for input
r_min, r_max = -10.0, 10.0
# sample input range uniformly at 0.1 increments
inputs = arange(r_min, r_max, 0.1)
# compute targets
results = objective(inputs)
# create a line plot of input vs result
pyplot.plot(inputs, results)
# define optimal input value
x_optima = 0.67956
# draw a vertical line at the optimal input
pyplot.axvline(x=x_optima, ls='--', color='red')
# show the plot
pyplot.show()

        运行示例将创建函数的折线图，并用红线标记最优值。

多模态函数

        多模态函数是指具有多个“模态”或最优值（例如谷值）的函数。

       多峰函数是非凸的。可能存在一个全局最优解和一个或多个局部最优解或欺骗最优解。 或者，可能存在多个全局最优值，即导致函数的相同最小输出的多个不同输入。让我们看几个多模态函数的例子。

多模式函数 1

      范围限制在 -2.7 和 7.5 之间，最佳输入值为 5.145735。

# multimodal function
from numpy import sin
from numpy import arange
from matplotlib import pyplot# objective function
def objective(x):return sin(x) + sin((10.0 / 3.0) * x)# define range for input
r_min, r_max = -2.7, 7.5
# sample input range uniformly at 0.1 increments
inputs = arange(r_min, r_max, 0.1)
# compute targets
results = objective(inputs)
# create a line plot of input vs result
pyplot.plot(inputs, results)
# define optimal input value
x_optima = 5.145735
# draw a vertical line at the optimal input
pyplot.axvline(x=x_optima, ls='--', color='red')
# show the plot
pyplot.show()

         运行示例将创建函数的折线图，并用红线标记最优值。

多模式函数 2

       范围限定为 0.0 和 1.2，最佳输入值为 0.96609。

# multimodal function
from numpy import sin
from numpy import arange
from matplotlib import pyplot# objective function
def objective(x):return -(1.4 - 3.0 * x) * sin(18.0 * x)# define range for input
r_min, r_max = 0.0, 1.2
# sample input range uniformly at 0.01 increments
inputs = arange(r_min, r_max, 0.01)
# compute targets
results = objective(inputs)
# create a line plot of input vs result
pyplot.plot(inputs, results)
# define optimal input value
x_optima = 0.96609
# draw a vertical line at the optimal input
pyplot.axvline(x=x_optima, ls='--', color='red')
# show the plot
pyplot.show()

        运行示例将创建函数的折线图，并用红线标记最优值。

多模式函数 3

      范围限定在 0.0 和 10.0 之间，最佳输入值为 7.9787。

# multimodal function
from numpy import sin
from numpy import arange
from matplotlib import pyplot# objective function
def objective(x):return -x * sin(x)# define range for input
r_min, r_max = 0.0, 10.0
# sample input range uniformly at 0.1 increments
inputs = arange(r_min, r_max, 0.1)
# compute targets
results = objective(inputs)
# create a line plot of input vs result
pyplot.plot(inputs, results)
# define optimal input value
x_optima = 7.9787
# draw a vertical line at the optimal input
pyplot.axvline(x=x_optima, ls='--', color='red')
# show the plot
pyplot.show()

不连续函数（非平滑）

      函数可能具有不连续性，这意味着函数输入的平滑变化可能会导致输出的非平滑变化。 我们可能将具有此属性的函数称为非平滑函数或不连续函数。有许多不同类型的不连续性，但一个常见的例子是函数输出值的跳跃或方向急剧变化，这在函数图中很容易看出。

       不连续函数，范围限定在 -2.0 和 2.0 之间，最佳输入值为 1.0。

# non-smooth optimization function
from numpy import arange
from matplotlib import pyplot# objective function
def objective(x):if x > 1.0:return x**2.0elif x == 1.0:return 0.0return 2.0 - x# define range for input
r_min, r_max = -2.0, 2.0
# sample input range uniformly at 0.1 increments
inputs = arange(r_min, r_max, 0.1)
# compute targets
results = [objective(x) for x in inputs]
# create a line plot of input vs result
pyplot.plot(inputs, results)
# define optimal input value
x_optima = 1.0
# draw a vertical line at the optimal input
pyplot.axvline(x=x_optima, ls='--', color='red')
# show the plot
pyplot.show()

        运行示例将创建函数的折线图，并用红线标记最优值。

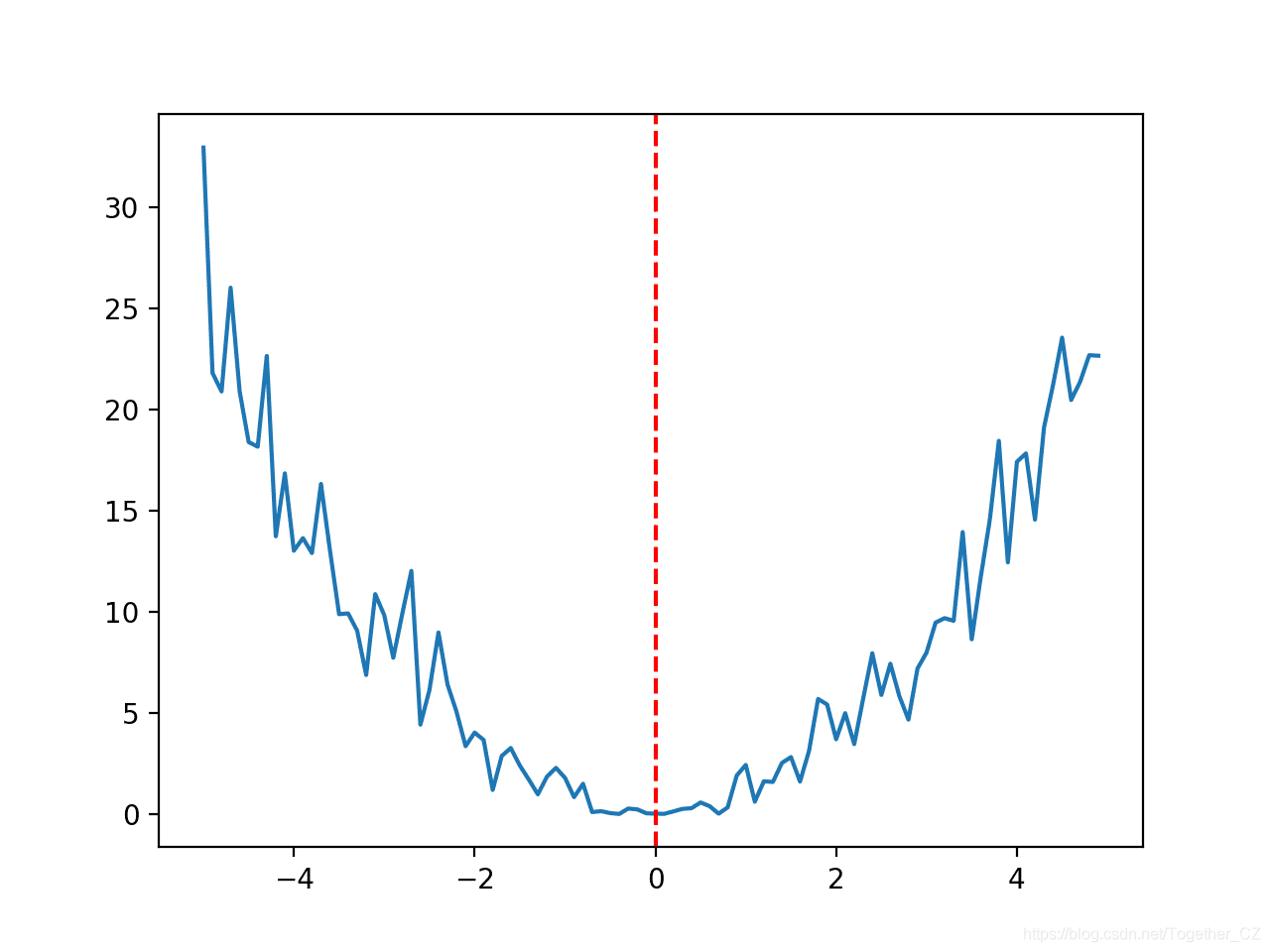
嘈杂的函数

       函数可能具有噪声，这意味着每个评估可能具有随机成分，每次都会稍微改变函数的输出。通过向输入值添加小的高斯随机数，可以使任何非噪声函数产生噪声。以下函数的范围限制为-5.0和5.0，最佳输入值为0.0。

# noisy optimization function
from numpy import arange
from numpy.random import randn
from matplotlib import pyplot# objective function
def objective(x):return (x + randn(len(x))*0.3)**2.0# define range for input
r_min, r_max = -5.0, 5.0
# sample input range uniformly at 0.1 increments
inputs = arange(r_min, r_max, 0.1)
# compute targets
results = objective(inputs)
# create a line plot of input vs result
pyplot.plot(inputs, results)
# define optimal input value
x_optima = 0.0
# draw a vertical line at the optimal input
pyplot.axvline(x=x_optima, ls='--', color='red')
# show the plot
pyplot.show()

        运行示例将创建函数的折线图，并用红线标记最优值。

 

 


http://www.ppmy.cn/news/149118.html

相关文章

数据结构—链表的相关理论点

数据结构—链表的相关理论点

链表（linked list）是一种常见的数据结构，用于实现电脑的动态内存分配。链表通过指针相互连接节点（Node），而该节点内保存了数据。 链表通常由头节点（head）和尾节点&#xff0…
阅读更多...
vue 单点登录的方法

vue 单点登录的方法

vue 单点登录的方法 当我们在使用 vue开发项目时，一般都是只有一个用户帐号，如果要实现多个帐号的单点登录，可以使用 Session和 LocalStorage这两个技术。这两个技术在实现单点登录时，都需要有一个用户名和一个密码，而…
阅读更多...
【Web服务器集群】基于Nginx搭建LNMP架构

【Web服务器集群】基于Nginx搭建LNMP架构

文章目录 一、安装 MySQL 数据库1. 安装Mysql环境依赖包2. 创建运行用户3. 编译安装4. 修改mysql 配置文件5. 更改mysql安装目录和配置文件的属主属组6. 设置路径环境变量7. 初始化数据库8. 添加mysqld系统服务9. 修改mysql 的登录密码10. 授权远程登录 二、编译安装 nginx 服务…
阅读更多...
Nginx-Host绕过复现

Nginx-Host绕过复现

目录 环境搭建： 第一种处理方式 第二种处理方式 第三种处理方式 原理依据：Nginx与PHP对Host处理方式不同 环境搭建： 1、提前安装完成nginxphpmysql，然后上传文件pwnhub到nginx/html下 2、修改nginx.conf配置文件&#xff1…
阅读更多...
信息安全导论

信息安全导论

信息安全导论1 计算机安全的特点 没有绝对的安全安全是一个动态实践的过程人是安全机制中最薄弱的环节 计算机安全的属性 Confidentiality 对信息或资源的内容或存在性的隐藏，使得信息不被授权或访问。Integrity数据在网络传输过程中，没有被第三方非…
阅读更多...
榨汁机方案开发

榨汁机方案开发

榨汁机方案开发一、全自动智能榨汁机方案总体设计 产品材料使用的是高硼硅玻璃，耐高温，不易变形，易清洗； 支持一键启动，完成之后摇晃瓶身，果汁更加细腻； 每种水果都有对应的榨取时间&#xff0c…
阅读更多...
拆解博朗一款剃须刀，质量真心差。德吹可以休已

拆解博朗一款剃须刀，质量真心差。德吹可以休已

话不多说直接上拆解图
阅读更多...
使用带参数的方法；举例：榨汁机

使用带参数的方法；举例：榨汁机

学习中不断求解，逻辑思维太乱，需要慢慢的整理，现在只能大概的了解知识点，所以这个简单的代码写出了繁杂的解释说明，这是希望加深自己对代码的理解，这是一位朋友教授的学习方法，感觉不错&#xf…
阅读更多...
最新文章

Copyright @ 2022~2023