🤩本文作者:大家好,我是paper jie,感谢你阅读本文,欢迎一建三连哦。
🥰内容专栏:这里是《C知识系统分享》专栏,笔者用重金(时间和精力)打造,基础知识一网打尽,希望可以帮到读者们哦。
🥴内容分享:本期会对C语言中的数据存储进行具体讲解,各位看官姥爷快搬好小板凳坐好叭。
😘:不要998,只要一键三连,三连买不了吃亏,买不了上当(写作不易,拜托拜托)。
目录
🎃本章介绍重点
🎀数据类型的介绍
🎑类型的基本归类
🏆整型在内存中的存储
🏀原码,反码,补码
⚾大小端介绍
🏓浮点数在内存中的存储
🪅有一个例子
🥌浮点数存储规则
🎯解析前面的题目
🎱分析代码
🎰总结
🎃本章介绍重点
1. 数据类型的详细介绍
2. 整型在内存中的存储:原码,反码,补码
3. 大小端字节序介绍及判断
4. 浮点型在内存中的存储解析
🎀数据类型的介绍
char //字符数据类型
short //短整型
int //整型
long //长整型
long long //更长的整型
float //单精度浮点型
double //双精度浮点型类型的意义:
使用这个类型开辟的内存空间的大小(大小决定了使用范围)
如何看待内存空间的视角
🎑类型的基本归类
整型家族:

注意:因为字符存储的时候,存的是ASCII码值,是整型,所以归类为整型家族
浮点数家族:

构造类型(自定义类型):

指针类型:

空类型:
void表示空类型(无类型)
通常用于函数的返回类型,函数的参数,指针类型。
🏆整型在内存中的存储
一个变量的创建是要在内存中开辟空间的,空间的大小是由不同的类型决定的。接下来我们谈谈数据在内存中开辟后是如何存储的?
比如 int a = 10;我们知道a分配到了4个字节的空间。但它是如何在内存中存储的呢?
下面我们来了解一下原码反码补码的概念:
🏀原码,反码,补码
计算机中有三种2进制的表现形式:原码,反码,补码。
三种表示方法都有符号位和数值位,首位为符号位,后面的都是数值位。符号位都是用0表示正数,1表示负数。
正数的原码反码补码都相同,但负数的原码反码补码都不相同
负数的原码反码补码计算方式:
原码: 直接按照正负数的形式翻译成二进制位就是原码
反码:符号位不变,原码的其他位取反
补码:反码加一
对于整型来说:数据存放内存中其实是存放的补码。为什么呢?
使用补码,可以将符号位和数值域统一处理。
同时,加法和减法也可以统一处理(cpu只有加法器)补码和原码相互转换,其运算过程是相同的,不需要额外的硬件电路。
这里给大家举例分析加深印象:
正数: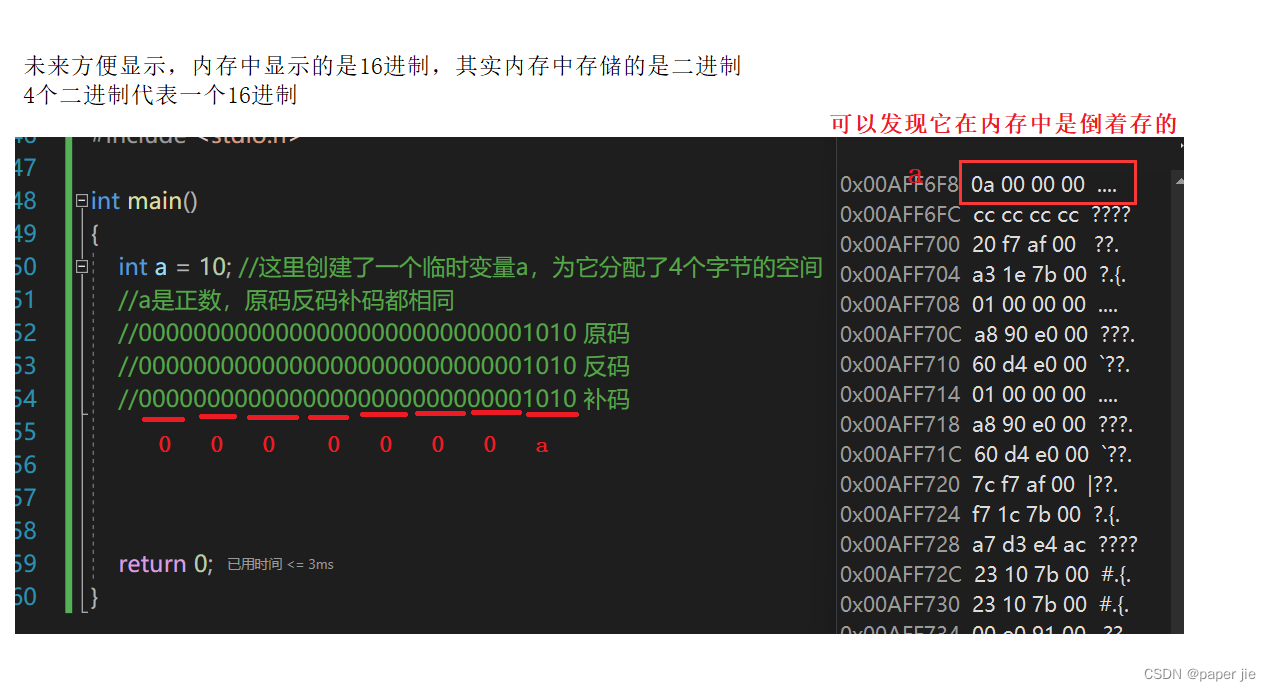
负数:

我们可以发现变量在内存中存储的是补码,但是顺序又不对。
这是为什么呢?
⚾大小端介绍
什么是大小端:
大端模式:数据的低位保存在内存的高地址位,数据的高位保存在内存的低地址位
小端模式:数据的低位保存在内存的低地址位,数据的高位保存在内存的高地址位
为什么有大小端:

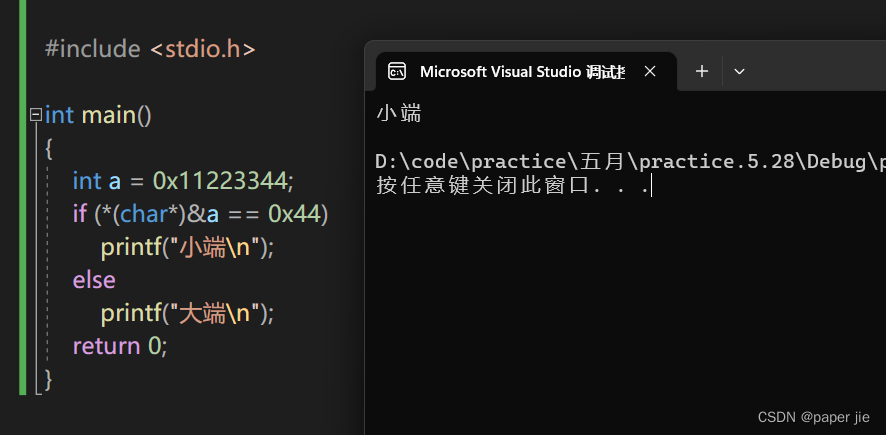
下面有一道百度的笔试题,是设计一个小程序来判断机器的字节序,我们一起来看看吧
我们设计是思路是用指针取出a的第一个地址,在用char解引用取出第一个字节地址里的内容和a的低位比较看是不是相等,是则小端,反之大端。
🏓浮点数在内存中的存储
常见的浮点数有两种:3.14159 1E10, 浮点数家族包括:float,double, long doudle类型。浮点数表示的范围:float.h中有定义
🪅有一个例子
这是一个有关浮点数和整数存储的例子,大家可以猜猜答案是多少?
#include <stdio.h>int main()
{int n = 9;float* pFloat = (float*)&n;printf("n的值为:%d\n", n);printf("*pFloat的值为:%f\n", *pFloat);*pFloat = 9.0;printf("num的值为:%d\n", n);printf("*pFloat的值为:%f\n", *pFloat);return 0;
}我想,应该有很多人会认为:
n的值为:9
*pFloat的值为: 9.000000
num的值为: 9
*pFfloat的值为:9.000000
让我们运行看看是不是这些答案叭!

咦,我们发现这些答案和我们猜的有极大的区别,这是为什么呢?我们缓一下,先来了解下面的知识,再回过头来看这个例子叭。
🥌浮点数存储规则
( -1)^S * M * 2^E(-1)^S表示符号位,当S=0,V为正数;当S=1,V为负数。M表示有效数字,大于等于1,小于2。2^E表示指数位。
画图举例:
IEEE 754中规定:
对于32位的浮点数,最高位的1位是符号位s,接着的8位是指数E,剩下的23位为有效数M

对于64位的浮点数,最高位的1位是符号位s,接着的11位是指数E,剩下的52位为有效数M


🎯解析前面的题目
为什么9变成浮点数就成了0.000000
首先,9的2进制是00000000000000000000000000001001,因为n是整数,将n强制类型转化给*pfloat,就相当于整数n的二进制被当做了浮点数在内存中的储存方法。我们将它拆分,得到s=0,E=00000000,M=00000000000000000001001。因为E全为0,所以当我们用科学计数法将它取出来就是 (-1)^0 * 0.00000000000000000001001*2^(-127). 我们可以发现它是一个无限接近小数的数,所以%f打印出来就是带有6位小数的0.000000

为什么n的值打印后是一个特别大的数
首先浮点数9.0的二进制是1001.0, 科学计数法为:(-1)^0*1.001*2^3, s=0 M=1.001 E=3
所以在9.0内存中存储就是:0 0000010 00100000000000000000000.这时以%d打印就是把9.0在内存中储存的数据当成了补码,还原成10进制打印出来。我们用计算机算一下发现它的十进制就是17,825,792

🎱分析代码
#include <stdio.h>int main()
{int n = 9;//00000000000000000000000000001001float* pFloat = (float*)&n;printf("n的值为:%d\n", n);printf("*pFloat的值为:%f\n", *pFloat);//s=0,E=00000000,M=00000000000000000001001//(-1)^0 * 0.00000000000000000001001*2^(-127) = 无穷小*pFloat = 9.0;//0 0000010 00100000000000000000000printf("num的值为:%d\n", n);//%d打印就是把9.0在内存中储存的数据当成了补码,还原成10进制打印出来printf("*pFloat的值为:%f\n", *pFloat);return 0;
}🎰总结
到这里我们对数据存储的深挖就结束了,通过这一次想必大家对数据存储的认识又提高了一个层次。下一章我们将会对指针进行更加细致的分析。




