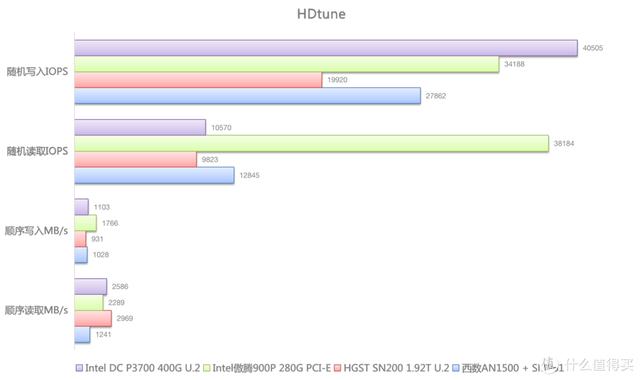
P3700 [CQOI2017]小Q的表格

Description

• 有一个无穷多行，无穷多列的表格，行列从 $1$ 开始标号，第 $a$ 行 $b$ 列有一个整数 $f(a,b)$；
• $f(a,b)$ 应满足：
  • $\forall a,b\in {\mathbb{N}}^{\ast },f(a,b)=f(b,a)$；
  • $\forall a,b\in {\mathbb{N}}^{\ast },b\cdot f(a,a+b)=(a+b)\cdot f(a,b)$。
• 初始时，$\forall a,b\in {\mathbb{N}}^{\ast },f(a,b)=ab$（显然这满足要求）；
• $m$ 次操作，每次给出 $4$ 个整数 $a,b,x,k$，表示令 $f(a,b)\leftarrow x$，然后把它能够波及到的所有格子全部修改，保证修改之后所有格子的数仍然都是整数，修改完成后计算前 $k$ 行前 $k$ 列里所有数的和 $\mathrm{m}\mathrm{o}\mathrm{d}(10^9+7)$；
• $1\le m\le 10^4,1\le a,b,k\le n\le 4\times 10^6,0\le x<10^{18}$。

Solution

对于性质 $2$，直接看是不会有任何思路的。

我们尝试对式子进行移项：
$$\begin{gathered} b\cdot f(a,a+b)=(a+b)\cdot f(a,b) \\ \frac{f(a,a+b)}{a+b}=\frac{f(a,b)}{b} \end{gathered}$$
根据性质 $1$，也就是说，当 $a>b$ 时，有
$$\frac{f(a,b)}{a}=\frac{f(b,a\mathrm{m}\mathrm{o}\mathrm{d}b)}{a\mathrm{m}\mathrm{o}\mathrm{d}b}$$
回忆辗转相除法的公式：
$$\gcd (a,b)=\gcd (b,a\mathrm{m}\mathrm{o}\mathrm{d}b)$$
发现和上面长的很像。

我们再把这个式子改造一下：
$$\frac{f(a,b)}{a\cdot b}=\frac{f(b,a\mathrm{m}\mathrm{o}\mathrm{d}b)}{b\cdot (a\mathrm{m}\mathrm{o}\mathrm{d}b)}$$
辗转相除法的最后一步是
$$\gcd (a,b)=\gcd (\gcd (a,b),0)$$
而这里要求 $a,b>0$，即
$$\gcd (a,b)=\gcd (\gcd (a,b),\gcd (a,b))$$
体现在原式中就是
$$\frac{f(a,b)}{a\cdot b}=\frac{f(\gcd (a,b),\gcd (a,b))}{\gcd (a,b{)}^2}$$
即
$$f(a,b)=\frac{ab\cdot f(\gcd (a,b),\gcd (a,b))}{\gcd (a,b{)}^2}$$
对于查询操作：
$$\begin{array}{rl}ans& =\sum _{d=1}^k\sum _{i=1}^k\sum _{j=1}^k\frac{ij\cdot f(d,d)}{d^2}[\gcd (i,j)=d]\\ & =\sum _{d=1}^{k}f(d,d)\sum _{i=1}^{\lfloor \frac{k}{d}\rfloor }i\sum _{j=1}^{\lfloor \frac{k}{d}\rfloor }j[\gcd (i,j)=1]\end{array}$$
根据
$$n\sum _{i=1}^{n}i[\gcd (i,n)=1]=n\cdot \frac{n\phi (n)+\epsilon (n)}{2}$$
发现这里 $j$ 可能大于 $i$，根据对称性乘 $2$ 即可。

但所有 $i=j$ 的情况都被重复算了 $2$ 次；不过对于 $i=j>1$ 的情况，$\gcd (i,j)\ne 1$，本身不会产生贡献；只有 $i=j=1$ 的情况被重复算了。

实际上 $i=j=1$ 的贡献是 $1\times 1\times 1=1$，而 $\frac{1\times \phi (1)+\epsilon (1)}{2}\times 2=2$，解决方案是直接把 $\epsilon$ 给扔掉，这样 $\frac{1\times \phi (1)}{2}\times 2=1$ 而且对于 $i>1$ 的情况去掉 $\epsilon$ 没有影响。

综上，
$$\begin{array}{rl}\sum _{i=1}^{n}i\sum _{j=1}^{n}j[\gcd (i,j)]& =\sum _{i=1}^{n}i\cdot \frac{i\phi (i)}{2}\cdot 2\\ & =\sum _{i=1}^n{i}^2\phi (i)\end{array}$$
设其为 $g(n)$，发现 $g$ 可以 $\mathrm{O}(n)$ 预处理 $\mathrm{O}(1)$ 回答。

代回原式
$$ans=\sum _{d=1}^{k}f(d,d)g\left(\lfloor \frac{k}{d}\rfloor \right)$$
愉快地整除分块。

整除分块中要用到 $f(n,n)$ 的前缀和，那么修改直接用树状数组单点修改即可，查询就是区间查询。

查询是 $\mathrm{O}(m\sqrt{n}\log n)$ 的，而修改才 $\mathrm{O}(m\log n)$，虽然能过但很不优。

考虑有什么数据结构能做到 $\mathrm{O}(1)$ 查询：分块——但只能单点查询。

这也不难，把维护的东西改为前缀和，查询就是 $\mathrm{O}(1)$，修改就修改 $\gcd (a,b)\sim n$，是 $\mathrm{O}(\sqrt{n})$ 的。

具体地，题目中要 $f(a,b)\leftarrow x$，根据上面的公式就是
$$f(\gcd (a,b),\gcd (a,b))\leftarrow \frac{x\cdot \gcd (a,b{)}^2}{ab}$$
这样就做到了平衡——修改查询均为 $\mathrm{O}(m\sqrt{n})$，比树状数组不知道快了多少倍。

Code

//18 = 9 + 9 = 18.
#include <iostream>
#include <cstdio>
#include <cmath>
#define Debug(x) cout << #x << "=" << x << endl
typedef long long ll;
using namespace std;const int MOD = 1e9 + 7;
int add(int a, int b) {return (a + b) % MOD;}
int sub(int a, int b) {return (a - b + MOD) % MOD;}
int mul(int a, int b) {return (ll)a * b % MOD;}const int MAXN = 4e6 + 5;
typedef int arr[MAXN];struct DS
{arr L, R, belong, val, tag, a;void build(int n){int t = sqrt(n);for (int i = 1; i <= t; i++){L[i] = R[i - 1] + 1, R[i] = i * t;}if (R[t] < n){t++;L[t] = R[t - 1] + 1, R[t] = n;}for (int i = 1; i <= t; i++){for (int j = L[i]; j <= R[i]; j++){belong[j] = i;a[j] = mul(j, j);val[j] = add(val[j - 1], a[j]);}}}void update(int l, int r, int x){int k = sub(x, a[l]);a[l] = x;int p = belong[l], q = belong[r];if (p == q){for (int i = l; i <= r; i++){val[i] = add(val[i], k);}}else{for (int i = l; i <= R[p]; i++){val[i] = add(val[i], k);}for (int i = L[q]; i <= r; i++){val[i] = add(val[i], k);}for (int i = p + 1; i < q; i++){tag[i] = add(tag[i], k);}}}int query(int x){return add(val[x], tag[belong[x]]);}int GetSum(int l, int r){return sub(query(r), query(l - 1));}
}D;struct Math
{arr p, phi, g;bool vis[MAXN];void pre(int n){phi[1] = 1;for (int i = 2; i <= n; i++){if (!vis[i]){p[++p[0]] = i;phi[i] = i - 1;}for (int j = 1; j <= p[0] && i * p[j] <= n; j++){vis[i * p[j]] = true;if (i % p[j] == 0){phi[i * p[j]] = phi[i] * p[j];break;}phi[i * p[j]] = phi[i] * phi[p[j]];}}for (int i = 1; i <= n; i++){g[i] = add(g[i - 1], mul(mul(i, i), phi[i]));}}int gcd(int a, int b){if (!b){return a;}return gcd(b, a % b);}int block(int n){int res = 0;for (int l = 1, r; l <= n; l = r + 1){int k = n / l;r = n / k;res = add(res, mul(D.GetSum(l, r), g[k]));}return res;}
}M;int main()
{int m, n;scanf("%d%d", &m, &n);D.build(n), M.pre(n);while (m--){int a, b, k; ll xx;scanf("%d%d%lld%d", &a, &b, &xx, &k);int d = M.gcd(a, b);xx = xx / (a / d) / (b / d);int x = xx % MOD;D.update(d, n, x);printf("%d\n", M.block(k));}return 0;
}