【C++】二叉树的进阶

news/2024/12/22 9:03:46/

二叉树的进阶

  • 二叉搜索树
  • 概念
  • 操作实现
    • 创建树形结构
    • 拷贝构造函数
    • 构造函数
    • 析构函数
    • 赋值运算符重载
    • 循环版本
      • 查找
      • 插入
      • 删除
    • 递归版本
      • 查找
      • 插入
      • 删除
  • 应用
    • K模型
    • KV模型
    • 性能分析
  • 二叉树进阶面试题
    • 二叉树创建字符串
    • 二叉树的分层遍历I
    • 最近公共祖先
    • 二叉搜索树与双向链表
    • 前序遍历与中序遍历构造二叉树
    • 中序遍历与后序遍历构造二叉树
    • 二叉树的前序遍历(非递归)
    • 二叉树的中序遍历(非递归)
    • 二叉树的后序遍历(非递归)

二叉搜索树

概念

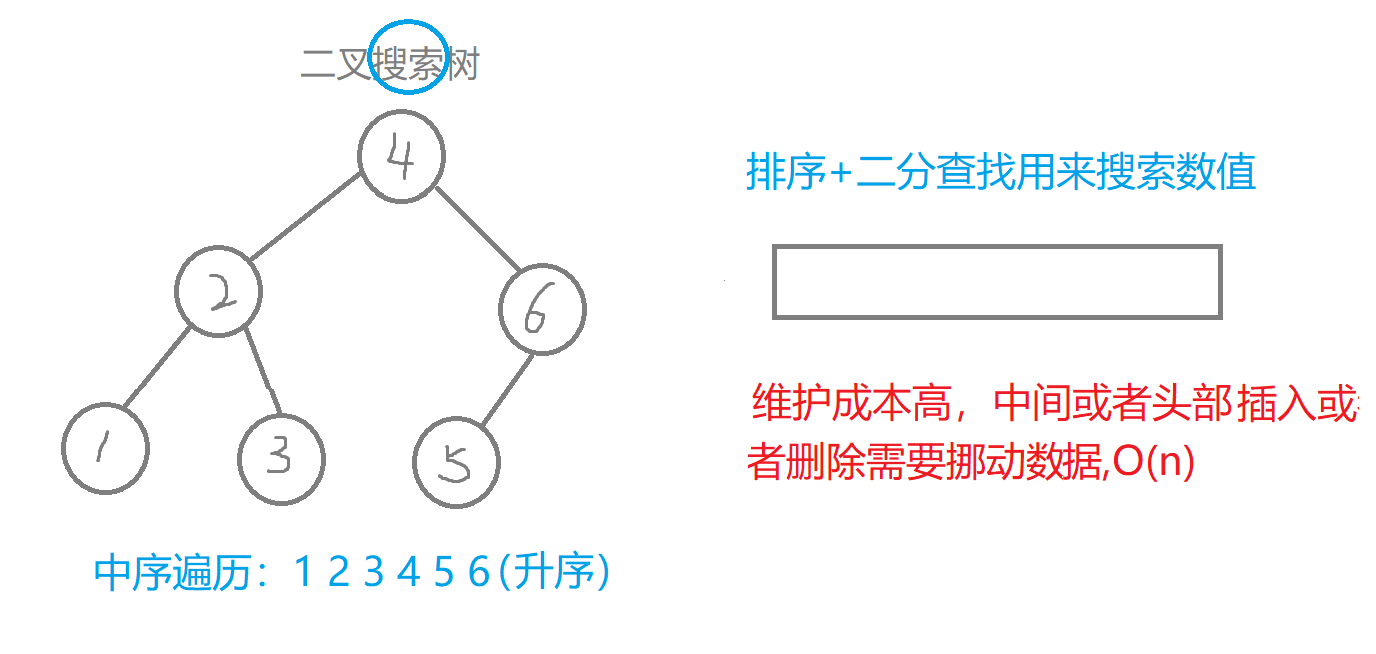
  1. 二叉搜索树：又称为二叉排序树或者二叉查找树，走中序遍历(左、根、右）打印二叉搜索树值为升序。
  2. 它可以空树。若它的左子树不为空，则左子树上所有节点的值都小于它的根节点的值。若它的右子树不为空，则右子树上所有节点的值都大于它的根节点的值。它的左右子树也分别为二叉搜索树。

image.png

操作实现

创建树形结构

template<class K>
struct BSTreeNode {   //二叉树的节点typedef BSTreeNode<K> Node;Node* _left;K _key;Node* _right;BSTreeNode(const K& key)  //构造函数:_left(nullptr), _right(nullptr), _key(key){}
};template<class K>
class BSTree {  //二叉树结构private:Node* _root = nullptr;
};

拷贝构造函数

BSTree(const BSTree<K>& t) //拷贝构造函数也是构造函数，写了拷贝构造，相当于显示写了构造，不能调默认构造
{/*Node* cur = t._root;  不能采用insert，因为cur不知道是往哪边走，走错了，树形结构会改变，不走，就死循环了while (cur){Insert(cur->_key);}*/_root = CopyNode(t._root);   //后序拷贝节点进行赋值
}Node* CopyNode(Node* root) //前序拷贝节点进行赋值
{if (root == nullptr) //递归的结束条件，满足，就会回退return nullptr;Node* newnode = new Node(root->_key);newnode->_left = CopyNode(root->_left); //递推newnode->_right = CopyNode(root->_right);return newnode;
}
  • 拷贝构造函数不显示写，内置类型为值拷贝，自定义类型会去调用它自己的拷贝构造函数，BSTreet2(t1)，不显示写拷贝构造，则t2和t1的_root指向同一块空间，若未显示写析构函数，程序不会崩溃，因为_root为Node*内置类型，最后由系统自动回收。若显示写析构函数，delete-》析构函数+free，会导致同一块空间被释放两次，造成程序崩溃。
  • 此处不能调用insert函数，因为cur不知道该往哪边走，走右边，会导致树形结构发生改变，就不是二叉搜索树了，走左边，走到空的时候，无法回退到上一个节点的右边。
  • 采用前序遍历(左、根、右），依次取t2对象中的节点，进行深拷贝。

构造函数

BSTree() = default;  //强制生成默认构造
  • BSTree t，编译器会去调用它的默认构造函数，若显示写了构造函数，编译器就不会自动生成默认构造函数，会导致编译器报错。拷贝构造函数是特殊的构造函数。
  • 注意：BSTree() = default，强制生成默认构造。

析构函数

~BSTree() //析构
{Destroy(_root); 
}void Destroy(Node* root)  //销毁树 
{if (root == nullptr)return;Destroy(root->_left); //后序遍历Destroy(root->_right);delete root;root = nullptr;
}

赋值运算符重载

BSTree<K>& operator=(BSTree<K> t) //赋值运算符{std:: swap(_root, t._root);return *this;}

循环版本

查找

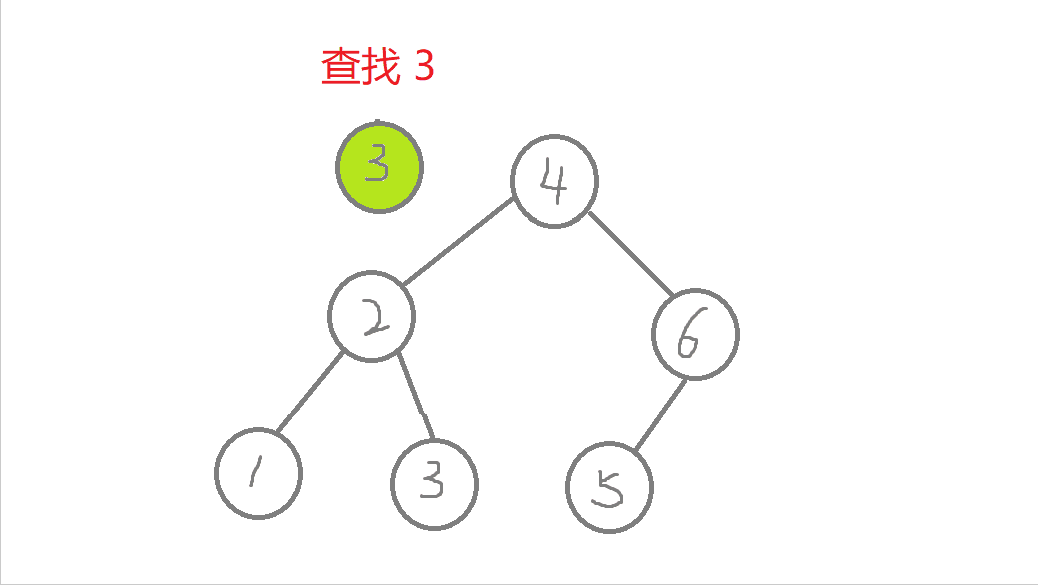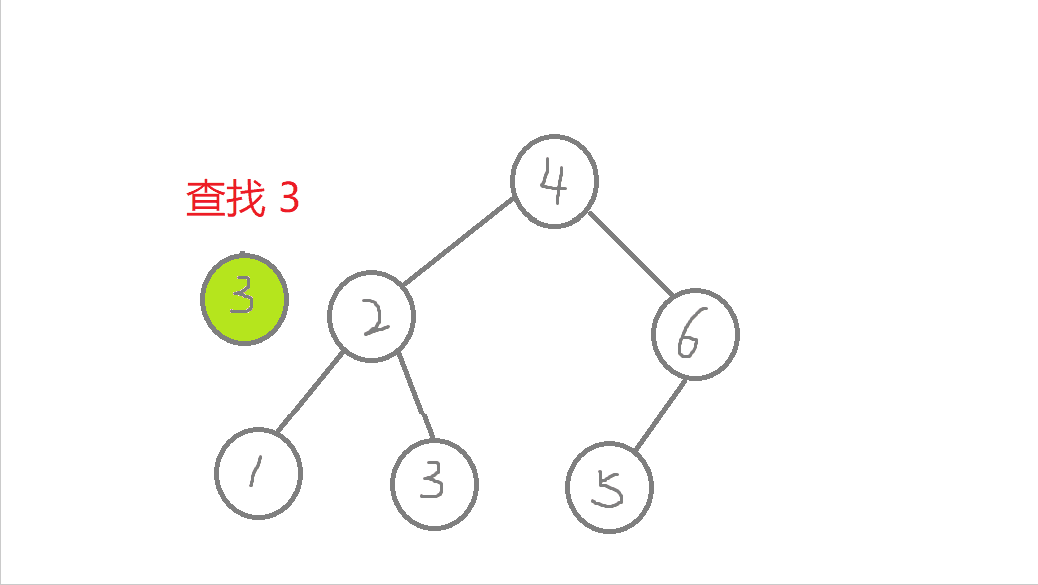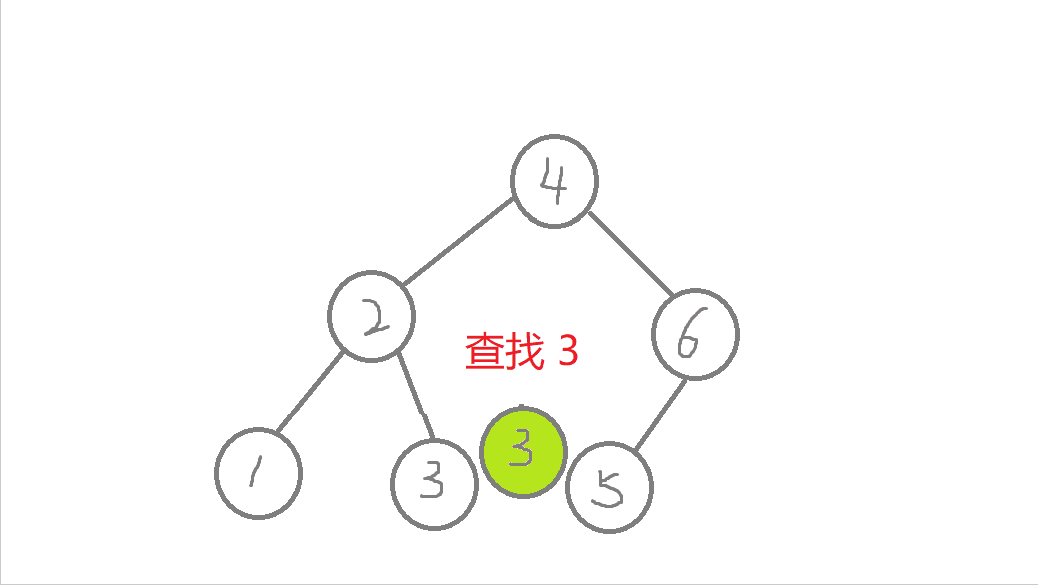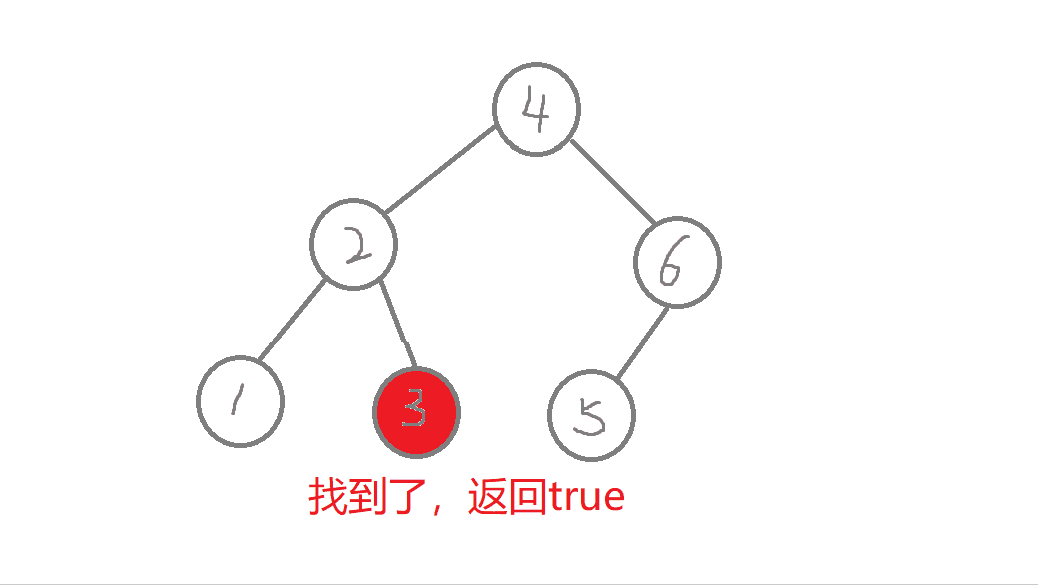
//非递归版本bool Find(const K& key)  //查找{Node* cur = _root;  //遍历二叉树while (cur){if (key > cur->_key)  //查找的值比根节点值大，往右进行查找cur = cur->_right;else if (key < cur->_key) //查找的值比根节点值小，往左进行查找cur = cur->_left;else    //查找到了return true;}return false;  //查找不到或者空树}
  • a. 从根节点开始查找，比较，比根节点的值大，则往右边查找，比根节点的值小，则往左边查找，
  • b.最多查找高度次。走到了空，这个值还没找到，这个值就不存在，则返回false。找到了就返回true。

搜索二叉树的find.gif

插入

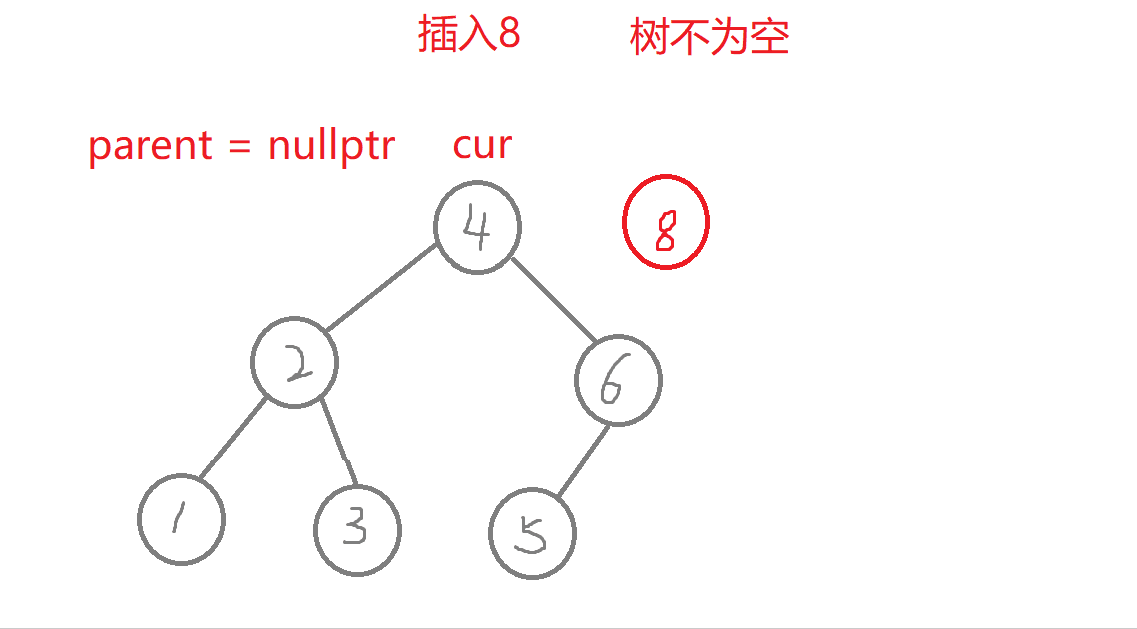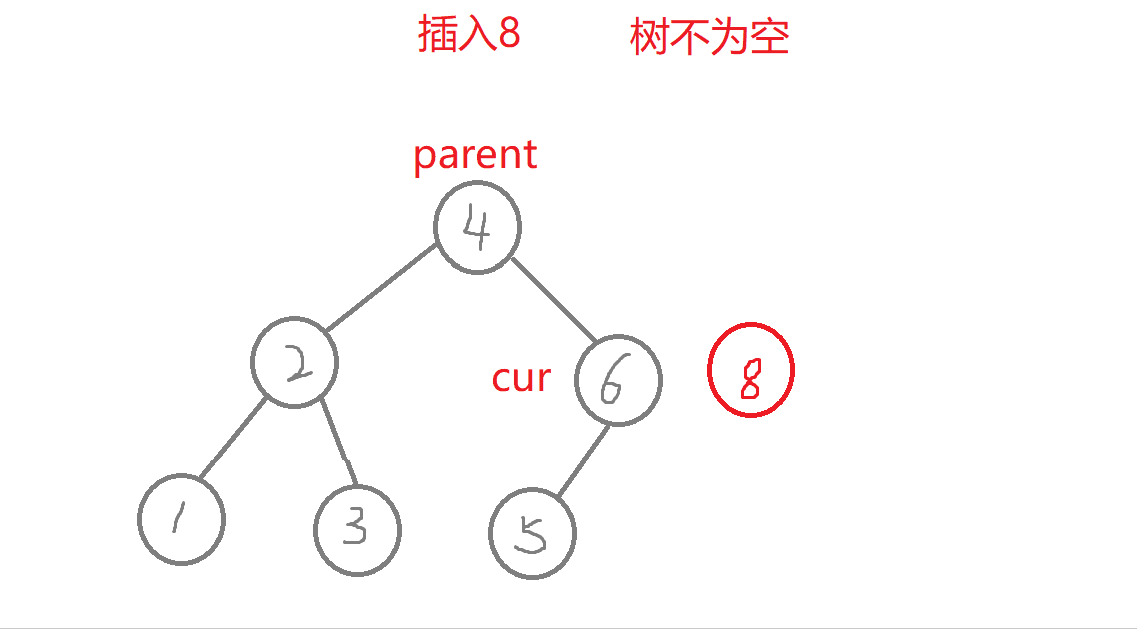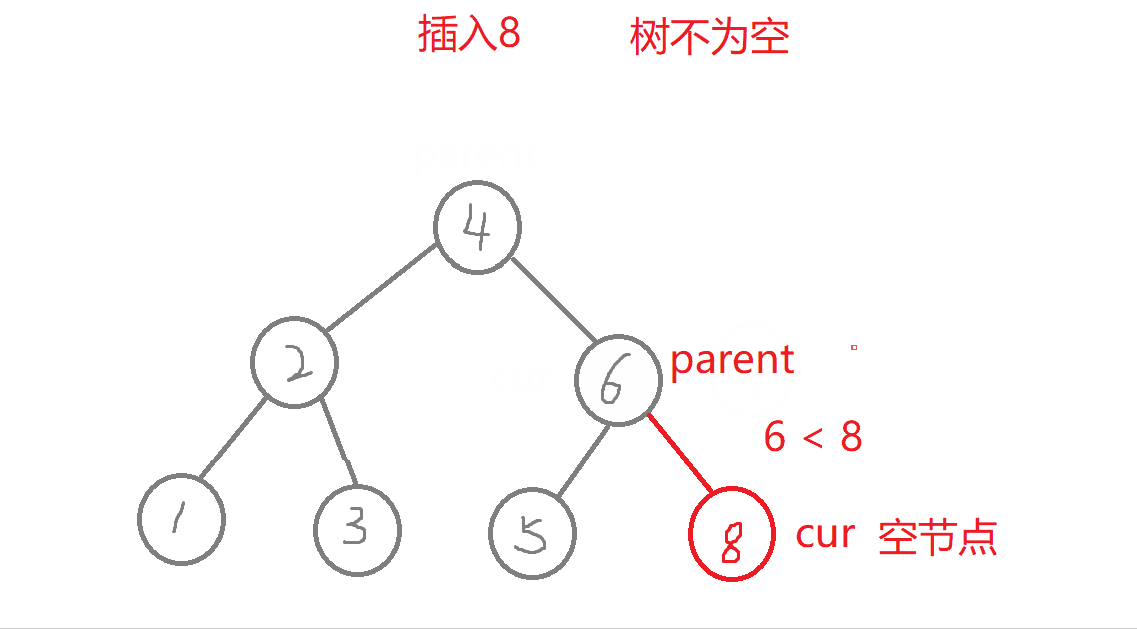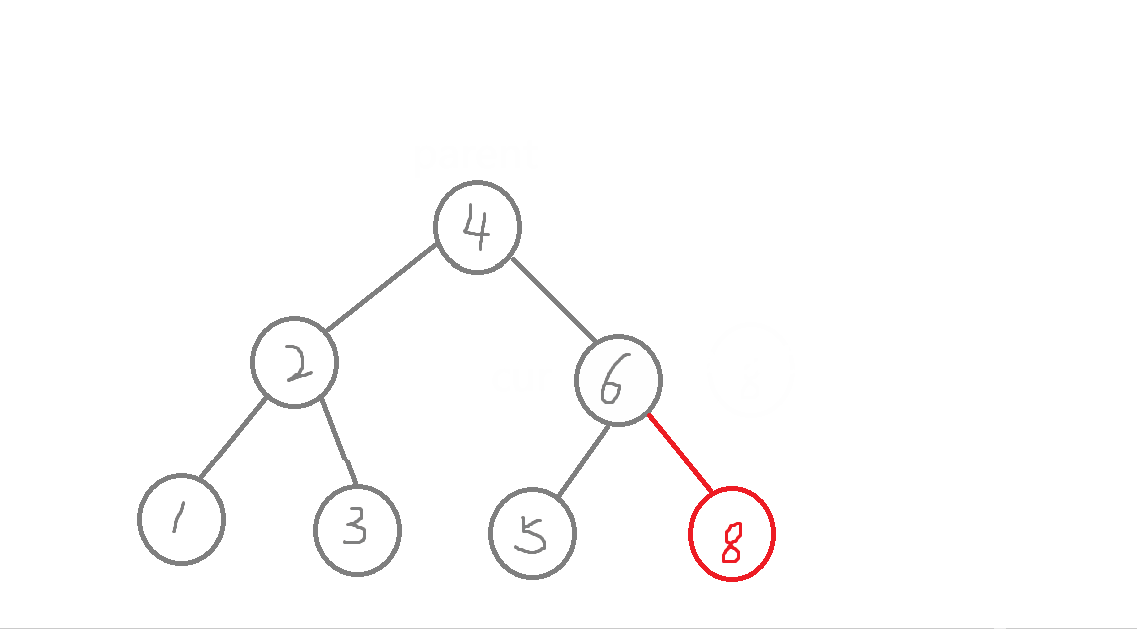
bool Insert(const K& key){Node* parent = nullptr;  //记录好新增节点在二叉树中的父节点Node* cur = _root;while (cur){if (key > cur->_key)  //查找的值比根节点值大，往右进行查找{parent = cur;cur = cur->_right;}else if (key < cur->_key) //查找的值比根节点值小，往左进行查找{parent = cur;cur = cur->_left;}elsereturn false;   //二叉搜索数中不运行出现同值，否则构成不了二叉搜素树}//new:开空间+构造函数cur = new Node(key);  //创建新节点，但此时cur值为随机值，cur为局部遍历，出了作用域就被销毁，若之后没有处理cur，会造成内存泄漏if (parent == nullptr)  //空树{_root = cur;return true;}if (parent->_key > key)  //新节点的链接parent->_left = cur;elseparent->_right = cur;return true;}
  • a.树为空，直接将赋值给_root。
  • b.树不为空，从根节点查找，比较，比根节点的值大，则往右边查找，比根节点的值小，则往左边查找，直到走到了空，在进行插入。
  • 注意：此处需要记录插入节点在二叉搜索树的父节点，因为cur = new Node(key)，会改变cur的值，cur此时不在是二叉树中的节点，cur为局部变量，出了作用域要销毁，则cur指向的那块空间无法找到，会造成内存泄漏，所以需要将其与父节点进行链接。

搜索二叉树的insert.gif

删除

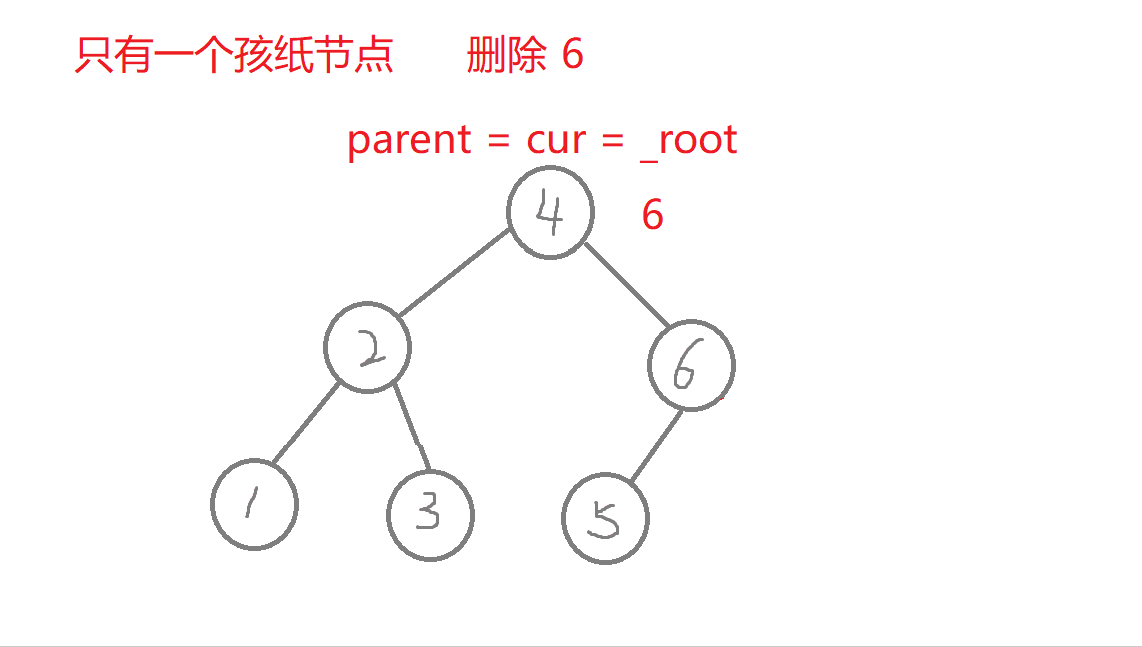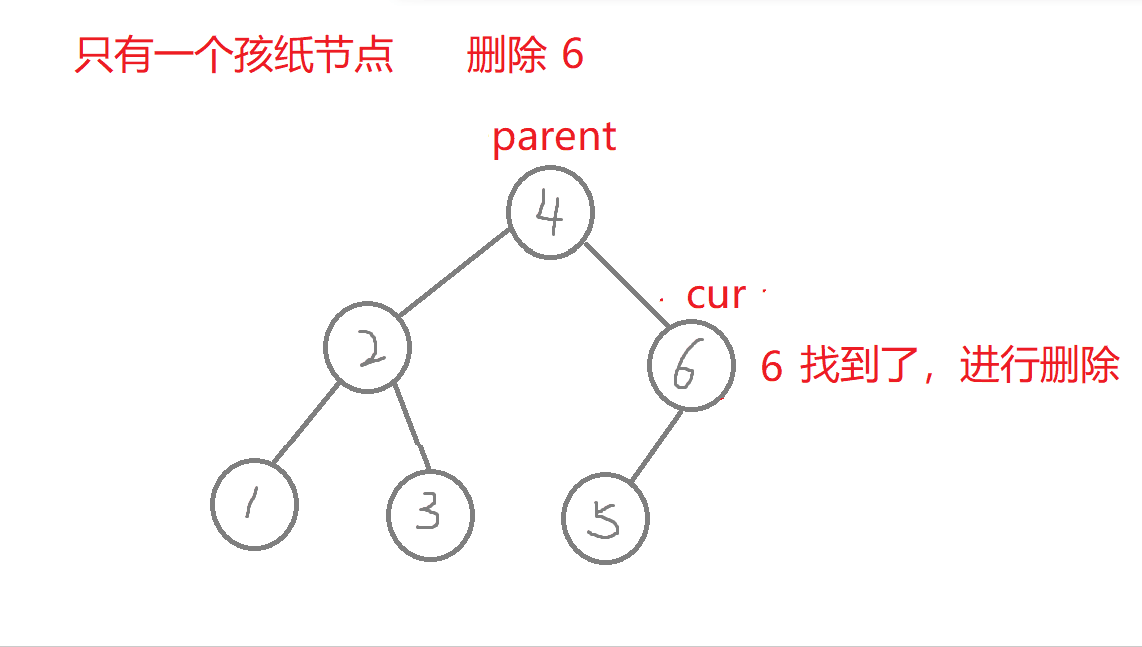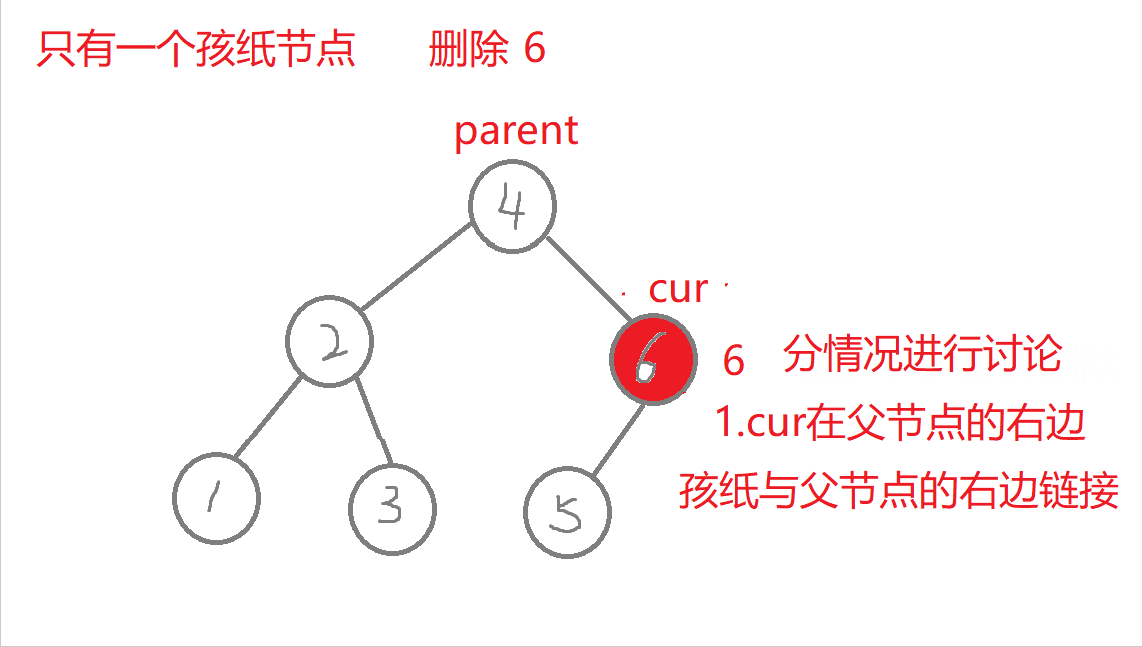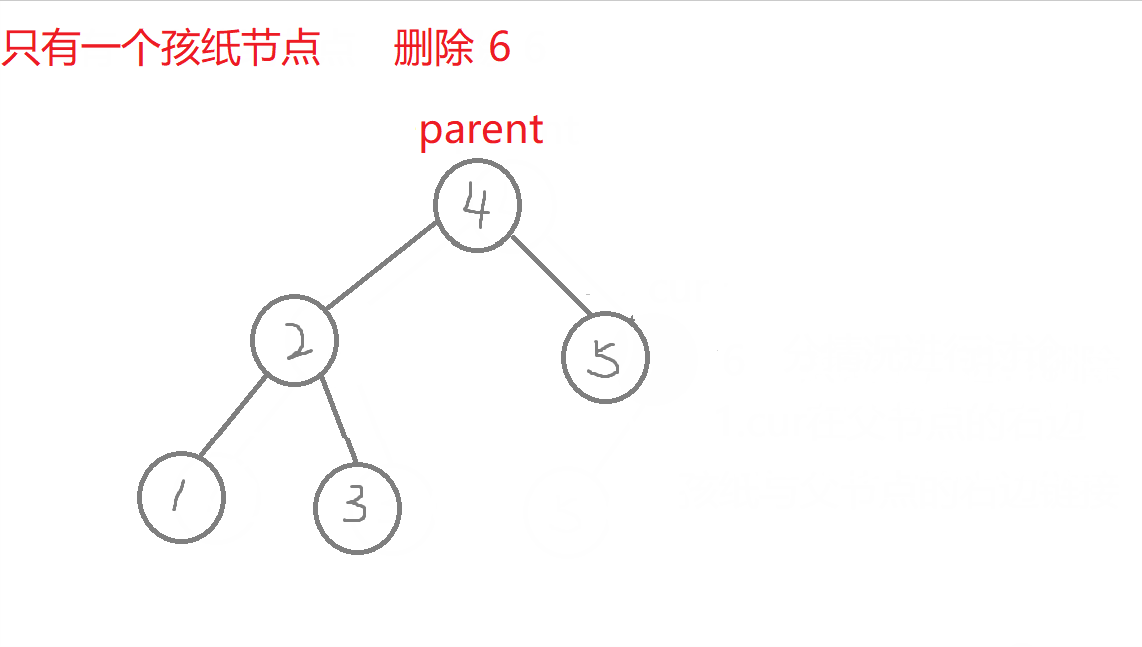
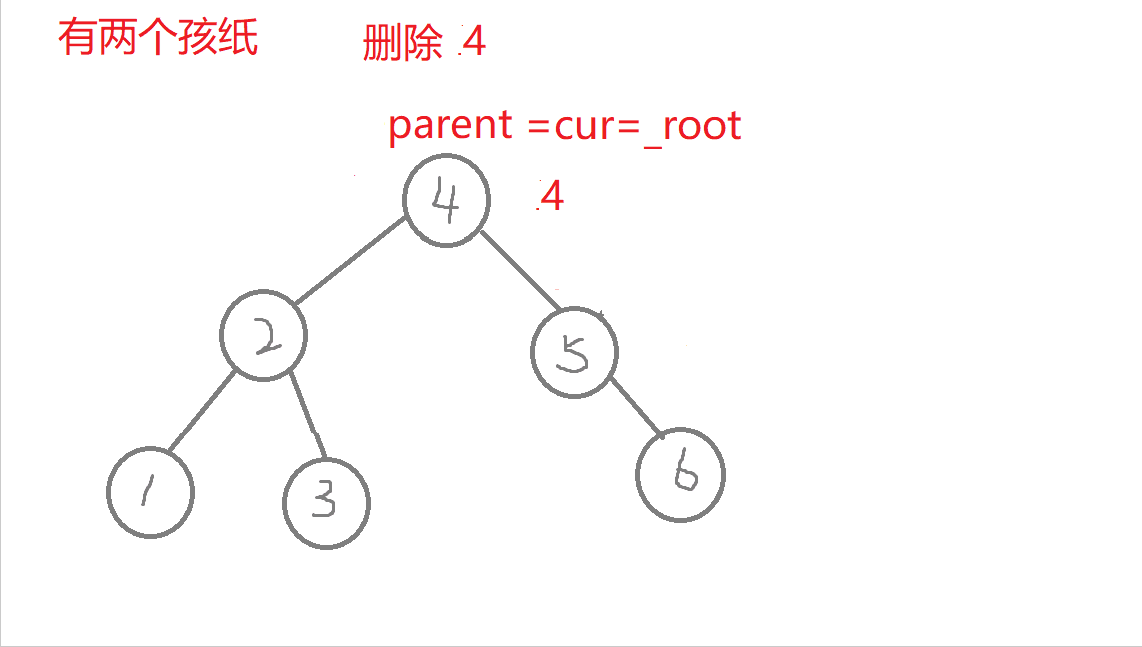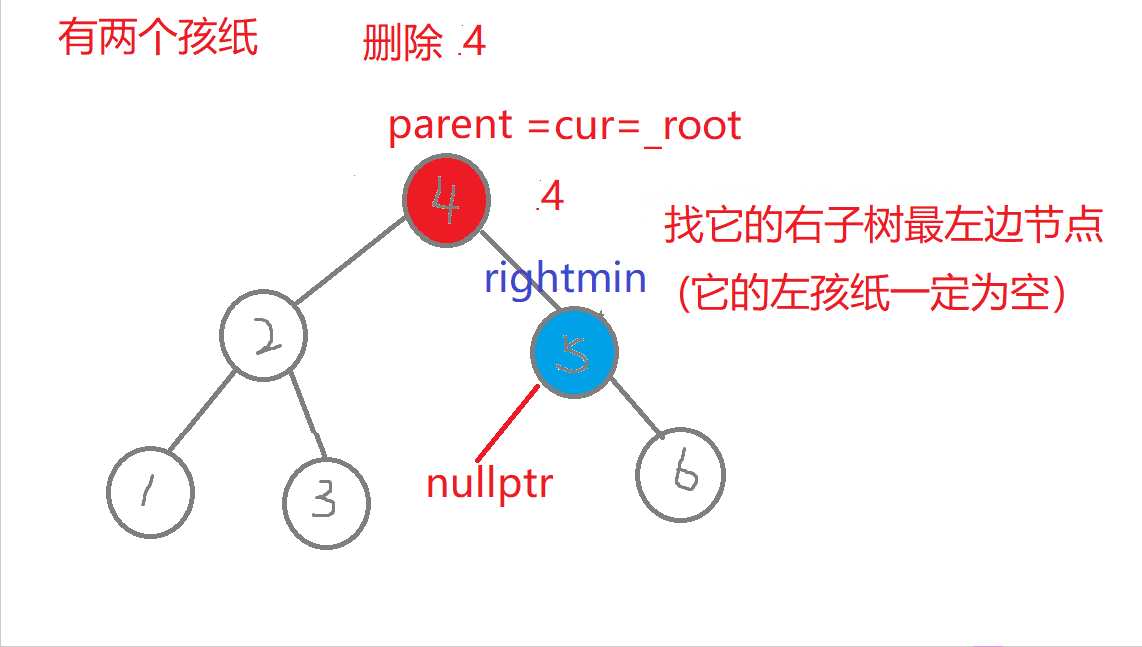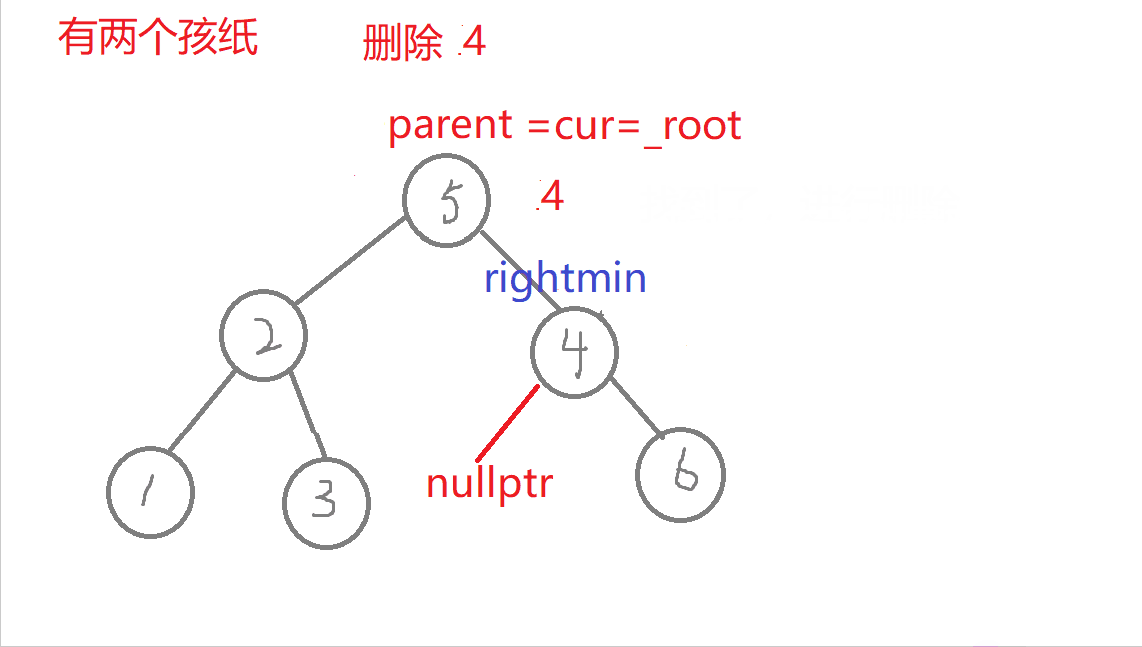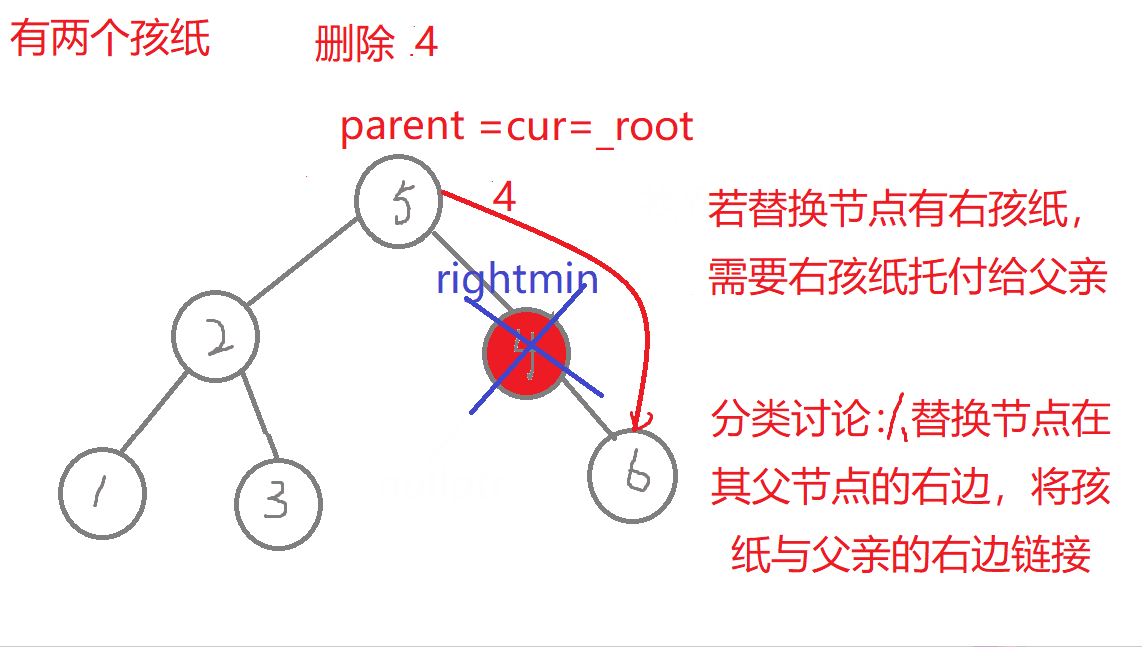
//叶子节点(无孩纸)、有一个孩纸—》将孩纸托付给父亲。 有两个孩纸-》替换法删除，找它的右子树的最左边节点值它的左节点一定为空）与它进行替换，转换成删别人bool erase(const K& key)  //删除{Node* parent = _root; //记录删除节点 或者 替换节点的父亲Node* cur = _root; while (cur){if (key > cur->_key)  //查找的值比根节点值大，往右进行查找{parent = cur;cur = cur->_right;}else if (key < cur->_key) //查找的值比根节点值小，往左进行查找{parent = cur;cur = cur->_left;}else  //找到了，进行删除{if (cur->_left == nullptr) //右边有一个孩纸{if (cur == _root) //删除根节点，需要换头_root = cur->_right;if (parent->_left == cur) //删除节点在根节点的左右子树，链接父节点的方式也不同parent->_left = cur->_right;elseparent->_right = cur->_right;delete cur;  cur = nullptr;return true;}else if (cur->_right == nullptr) {if (cur == _root) _root = cur->_left;if (parent->_left == cur)parent->_left = cur->_left;elseparent->_right = cur->_left;delete cur;cur = nullptr;return true;}else   //左右有两个孩纸-》替换法删除，找它的右子树中最右节点(它的左节点一定为空）{Node* rightmin = cur->_right;while (rightmin->_left)rightmin = rightmin->_left;cur->_key = rightmin->_key; //值进行替换if (parent->_right == rightmin) //删除节点可能在不同边，与父亲链接的情况也不同parent->_right = rightmin->_right;elseparent->_left = rightmin->_right;delete rightmin;rightmin = nullptr;return true;}}}return false;}
  • a.删除的节点有三种情况：叶子节点(无孩纸）、有一个孩纸(只有左孩纸或者只有右孩纸）、有两个孩纸。
  • b.叶子节点、有一个孩纸：将孩纸托付给父亲。
  • c.有两个孩纸：替换法删除，找它的右子树的最左边节点(它的左树一定为空)的值与它进行替换，转换成删替换节点了。

特殊情况：1.无孩纸节点、只有一个孩纸节点：删除根节点，此时需要换头，让root的下一个孩纸的节点。 2.只有一个孩纸节点：将孩子托付给父亲，孩纸和父亲的左边或者右边链接都可能，要分类讨论删除的节点在父节点的哪边，删除节点在父节点的哪边，孩纸就链接到哪边 。 3.两个孩纸节点：找最右节点rightmin，rightmin右孩子与父节点的左边或者右边都可能链接，要分类讨论rightmin在父节点的哪边，rightmin在父节点的哪边，rightmin右孩子孩纸就链接到哪边。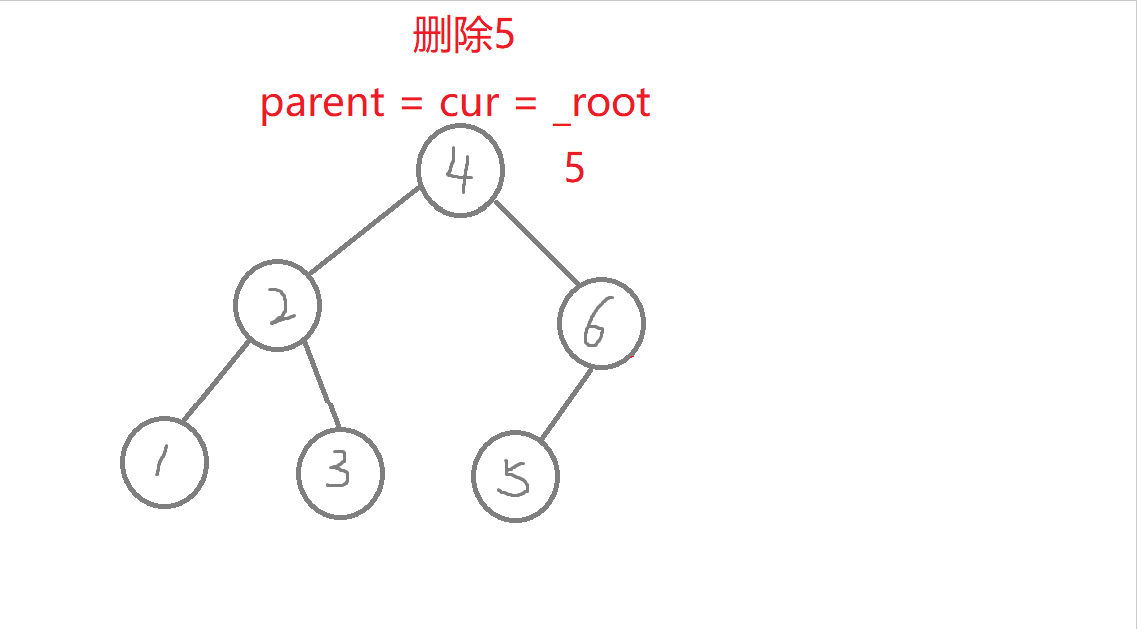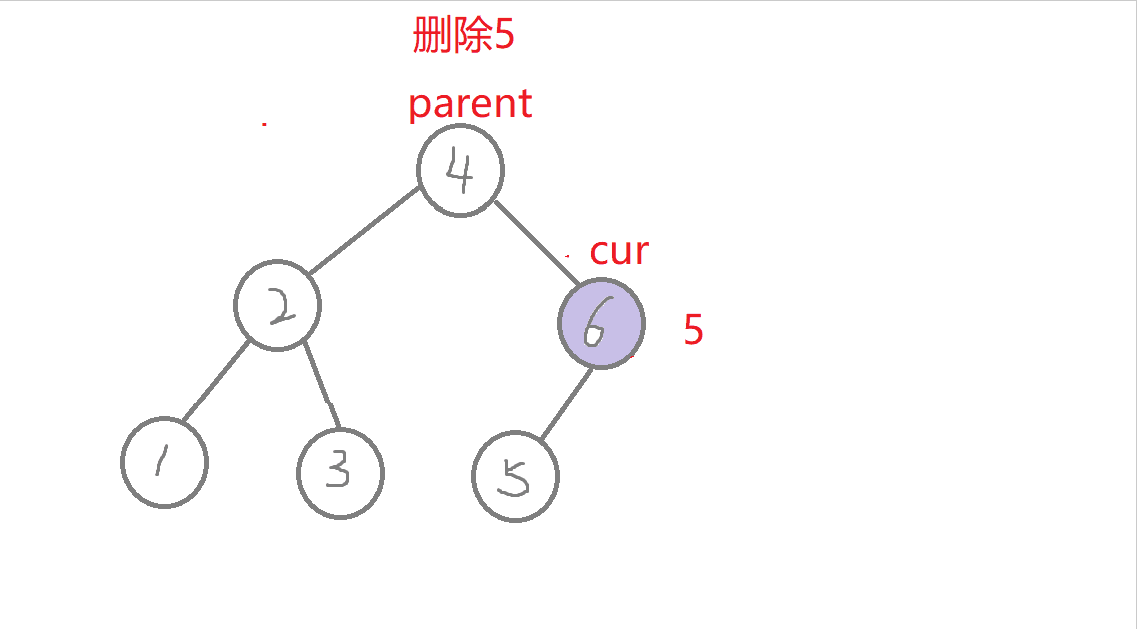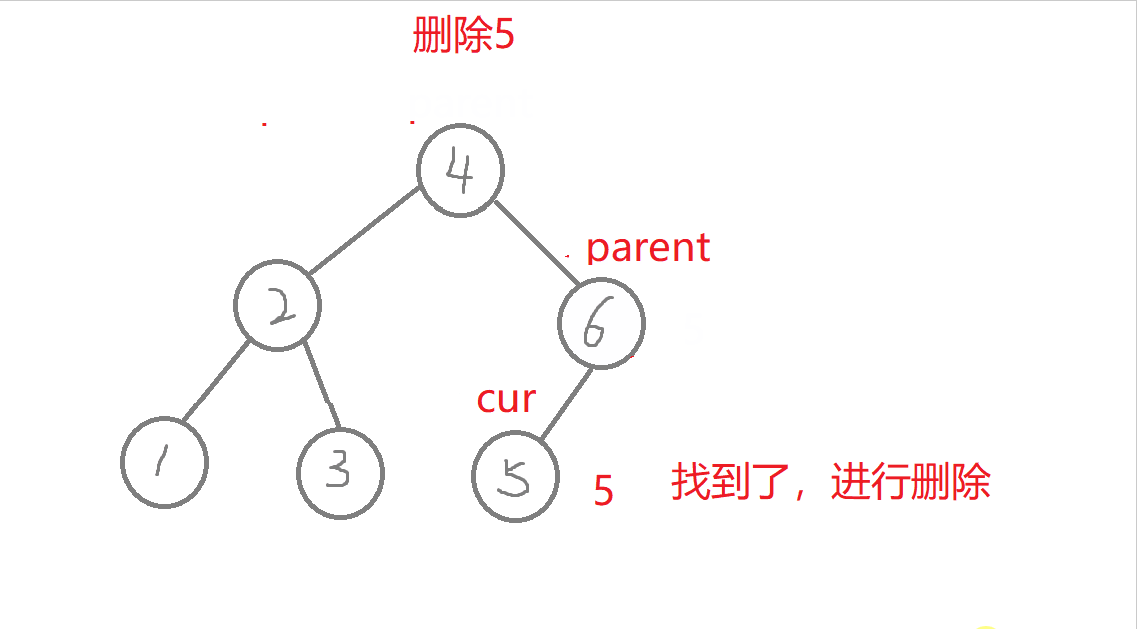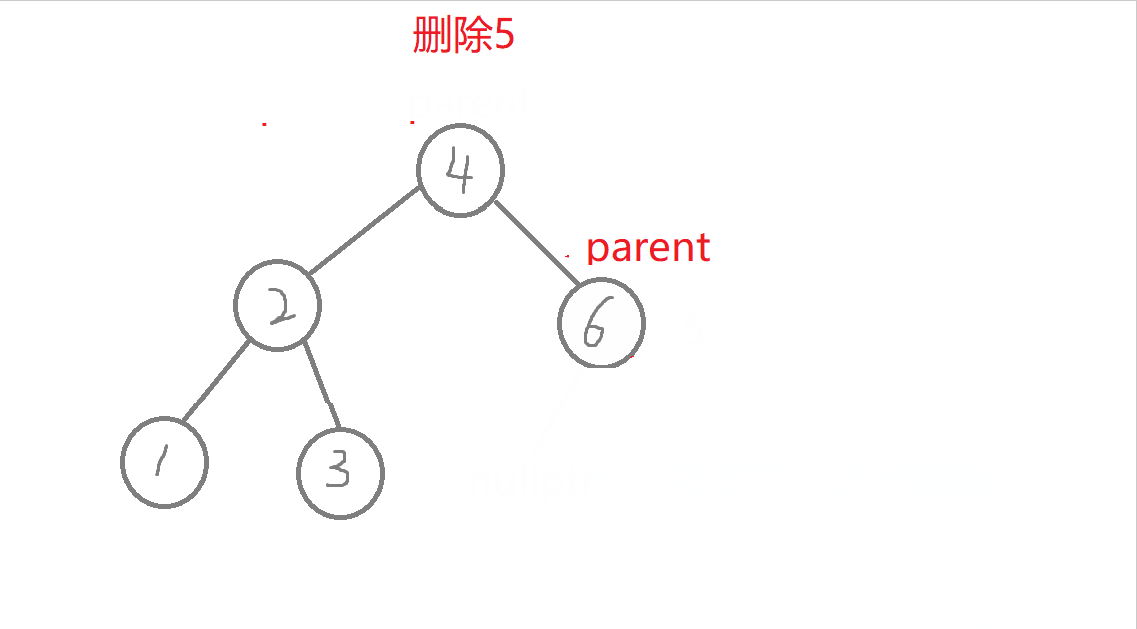
搜索二叉树的erase(无孩纸节点）.gif
搜索二叉树的erase(一个纸节点）.gif
搜索二叉树的erase(两个纸节点）.gif

递归版本

  • 二叉搜索树的操作因为要从根开始操作，所以在调用递归函数时，就需传递_root，但在类外不能访问私有成员_root， 解决方法：a. 通过创造Node* Getroot()成员函数(public)返回root，类外根据返回值直接传参调用递归函数。 b. 将递归函数封装在无参成员函数(public)中，类外调用无参函数，从而间接调用递归函数。

查找

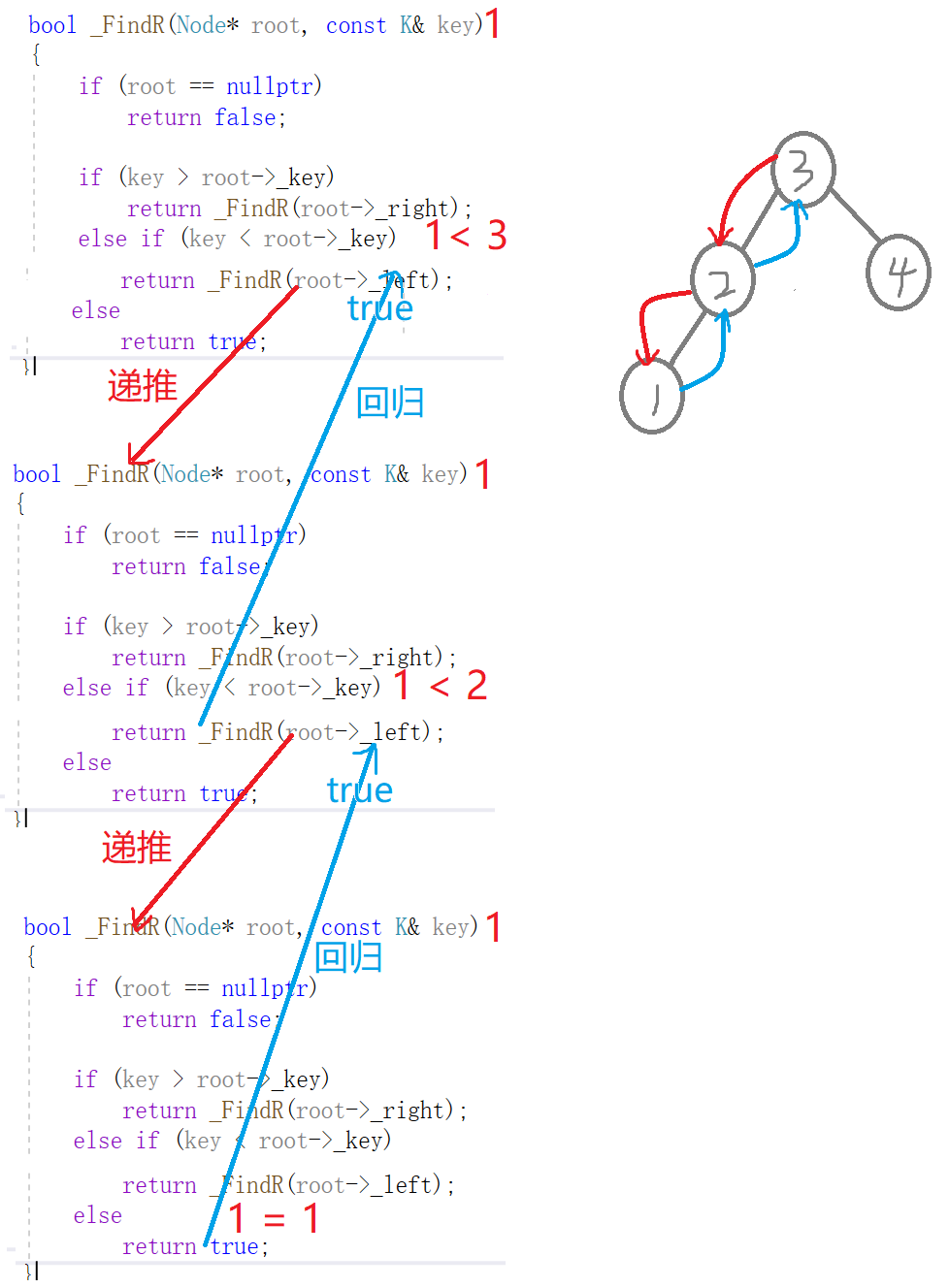
void FindR(const K& key)  
{_FindR(_root, key); //查找
}bool _FindR(Node* root, const K& key)
{if (root == nullptr)  //查找不到 或 空树return false;if (key > root->_key)  //查找的值比根节点值大，去右子树查找return _FindR(root->_right);else if (key < root->_key) //查找的值比根节点值小，去左子树查找return _FindR(root->_left);else   //找到了return true;
}

无标题.png

插入

bool _InsertR(Node*& root, const K& key){if (root == nullptr)  //进行插入{root = new Node(key);  //因为root为父亲孩纸的别名，直接就将父亲和新节点链接起来了return true;}if (key > root->_key)  //查找的值比根节点值大，去右子树查找return _InsertR(root->_right, key);else if (key < root->_key) //查找的值比根节点值小，去左子树查找return _InsertR(root->_left, key);else   //二叉搜索数中不运行出现同值，否则构成不了二叉搜素树return false;}

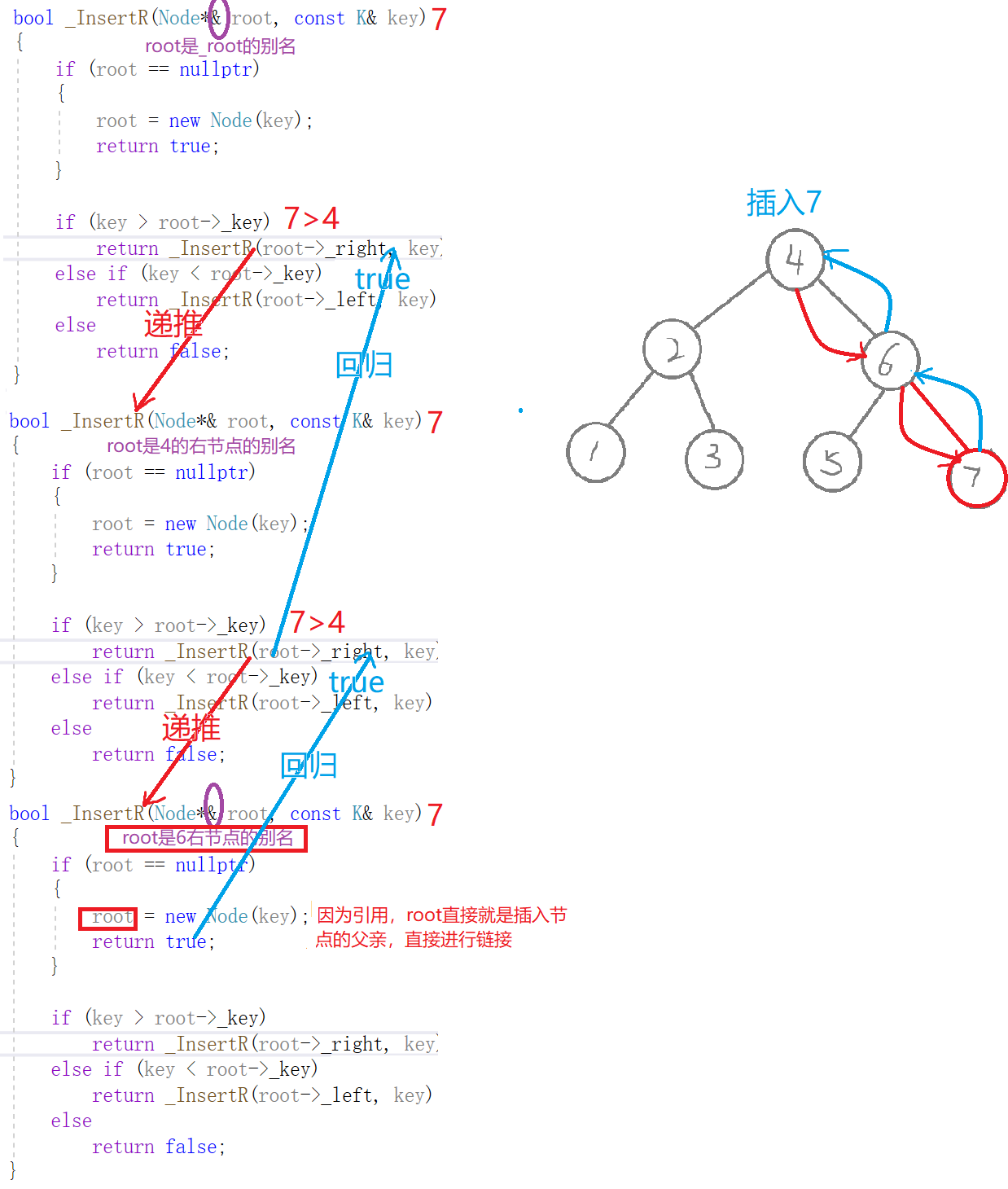
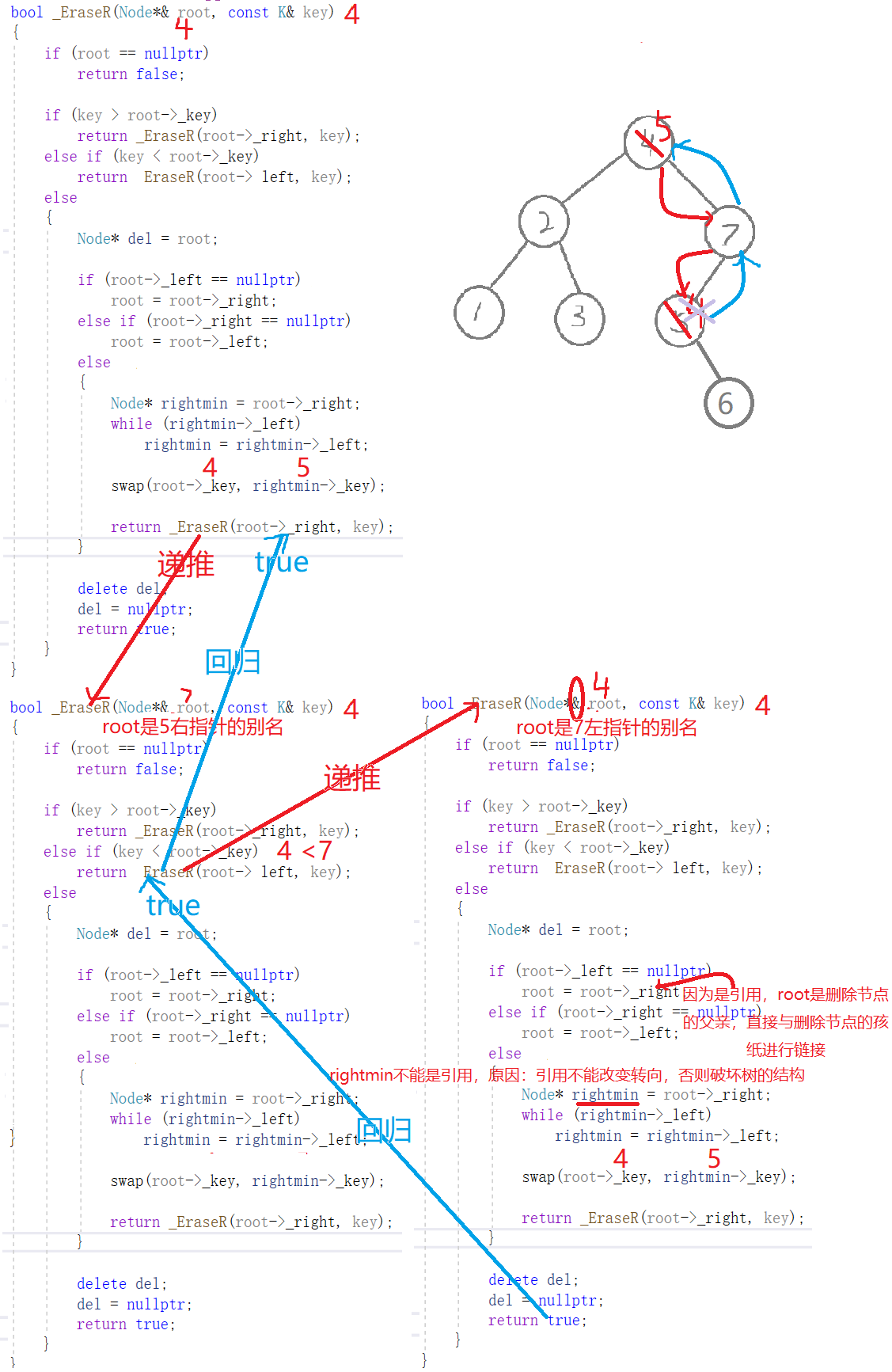
无标题.png

删除

bool _EraseR(Node*& root, const K& key){if (root == nullptr)return false;if (key > root->_key)  //查找的值比根节点值大，去右子树查找return _EraseR(root->_right, key);else if (key < root->_key) //查找的值比根节点值小，去左子树查找return _EraseR(root->_left, key);else   //找到了，进行删除{Node* del = root;  //记录删除的节点，防止父子链接时，该节点会被丢失if (root->_left == nullptr) //右边有一个孩纸root = root->_right;else if (root->_right == nullptr)root = root->_left;else   //左右有两个孩纸-》替换法删除，找它的右子树中最右节点(它的左节点一定为空）{Node* rightmin = root->_right;  //不能加引用，因为引用不能改变转向，否则会导致树的结构发生改变while (rightmin->_left)rightmin = rightmin->_left;swap(root->_key, rightmin->_key); //值进行替换return _EraseR(root->_right, key);}delete del;del = nullptr;return true;}}

无标题.png

应用

K模型

K模型：只有key作为关键码，结构中只需要存储Key。关键码即需要搜索key存不存在。

  • eg：小区车库，搜索车牌是否存在于小区车库体系中，控制车的进出。判断单词是拼写正确，搜索单词是否存在于单词库中。

KV模型

KV模型：每一个关键码key，都有与之对应的value，即<key, value>的键值对。

  • eg：统计单词的个数，<word，count>。英汉词典，<English，chinese>。
  • KV模型相比于K模型，只是在插入时多插入了value值，删除、查找都是对key进行操作，操作中的比较也是按key的值进行比较的。K模型类似于单身，KV模型类似于结婚。
#pragma once
#define _CRT_SECURE_NO_WARNINGS 1#include<iostream>
#include<algorithm>using namespace std;template<class K, class V>  //KV模型
struct BSTreeNode {   //二叉树的节点typedef BSTreeNode<K, V> Node;Node* _left;K _key;V _value;Node* _right;BSTreeNode(const K& key,const V& value)  //构造函数:_left(nullptr), _right(nullptr), _key(key),_value(value){ }
};template<class K, class V>
class BSTree {  //二叉树结构
public:typedef BSTreeNode<K, V> Node;~BSTree() //析构{Destroy(_root);}BSTree() = default;  //强制生成默认构造BSTree(const BSTree<K, V>& t) //拷贝构造函数也是构造函数，写了拷贝构造，相当于显示写了构造，不能调默认构造{  /*Node* cur = t._root;  不能采用insert，因为cur不知道是往哪边走，走错了，树形结构会改变，不走，就死循环了while (cur){Insert(cur->_key);}*/_root = CopyNode(t._root);   //前序拷贝节点进行赋值}BSTree<K, V>& operator=(BSTree<K, V> t) //赋值运算符{std:: swap(_root, t._root);return *this;}Node* Find(const K& key)  //查找 {Node* cur = _root;  //遍历二叉树while (cur){if (key > cur->_key)  //查找的值比根节点值大，往右进行查找cur = cur->_right;else if (key < cur->_key) //查找的值比根节点值小，往左进行查找cur = cur->_left;else    //查找到了 return cur;  //注意：返回节点的指针，目的—》通过key查找到value}return nullptr;  //查找不到或者空树}bool Insert(const K& key, const V& value)  //插入{Node* parent = nullptr;  //记录好新增节点在二叉树中的父节点Node* cur = _root;while (cur){if (key > cur->_key)  //查找的值比根节点值大，往右进行查找{parent = cur;cur = cur->_right;}else if (key < cur->_key) //查找的值比根节点值小，往左进行查找{parent = cur;cur = cur->_left;}elsereturn false;   //二叉搜索数中不运行出现同值，否则构成不了二叉搜素树}//new:开空间+构造函数cur = new Node(key, value);  //创建新节点，但此时cur值为随机值，cur为局部遍历，出了作用域就被销毁，若之后没有处理cur，会造成内存泄漏if (parent == nullptr)  //空树{_root = cur;return true;}if (parent->_key > key)  //新节点的链接parent->_left = cur;elseparent->_right = cur;return true;}//叶子节点(无孩纸)、有一个孩纸—》将孩纸托付给父亲。 有两个孩纸-》替换法删除，找它的右子树的最左边节点值它的左节点一定为空）与它进行替换，转换成删别人bool erase(const K& key)  //删除{Node* parent = _root; //记录删除节点 或者 替换节点的父亲Node* cur = _root; while (cur){if (key > cur->_key)  //查找的值比根节点值大，往右进行查找{parent = cur;cur = cur->_right;}else if (key < cur->_key) //查找的值比根节点值小，往左进行查找{parent = cur;cur = cur->_left;}else  //找到了，进行删除{if (cur->_left == nullptr) //右边有一个孩纸{if (cur == _root) //删除根节点，需要换头_root = cur->_right;if (parent->_left == cur) //删除节点在根节点的左右子树，链接父节点的方式也不同parent->_left = cur->_right;elseparent->_right = cur->_right;delete cur;  cur = nullptr;return true;}else if (cur->_right == nullptr) {if (cur == _root) _root = cur->_left;if (parent->_left == cur)parent->_left = cur->_left;elseparent->_right = cur->_left;delete cur;cur = nullptr;return true;}else   //左右有两个孩纸-》替换法删除，找它的右子树中最右节点(它的左节点一定为空）{Node* rightmin = cur->_right;while (rightmin->_left)rightmin = rightmin->_left;cur->_key = rightmin->_key; //值进行替换if (parent->_right == rightmin) //删除节点可能在不同边，与父亲链接的情况也不同parent->_right = rightmin->_right;elseparent->_left = rightmin->_right;delete rightmin;rightmin = nullptr;return true;}}}return false;}void InorderKV()   //KV模型打印{_InorderKV(_root);cout << endl;}private:void _InorderKV(Node* root)   //KV模型打印{if (root == nullptr)return;_InorderKV(root->_left);cout << root->_key << ' ' << root->_value << endl;_InorderKV(root->_right);}Node* _root = nullptr;
};

oid test5()  //kv模型-》查找单词的个数
{ BSTree<string, int> t;string s[] = { "苹果", "香蕉", "葡萄","梨子","苹果","苹果","香蕉","苹果" };for (auto& e : s){auto it = t.Find(e); if (it)it->_value += 1;elset.Insert(e, 1);}t.InorderKV(); //KV模型打印
}int main()
{test5();return 0;
}

image.png

void test6()  //kv模型-》英汉词典
{BSTree<string, string> dict;dict.Insert("see", "看");dict.Insert("eat", "吃");dict.Insert("left", "左");string str;while (cin >> str){auto it = dict.Find(str);if (it)cout << "中文翻译: " << it->_value << endl;elsecout << "单词不存在" << endl;}
}

image.png

  • 相较于K模型，改动的地方为Insert(key, value)、Node* Find(root, key)（返回节点的指针，目的—》通过key查找到value）。

性能分析

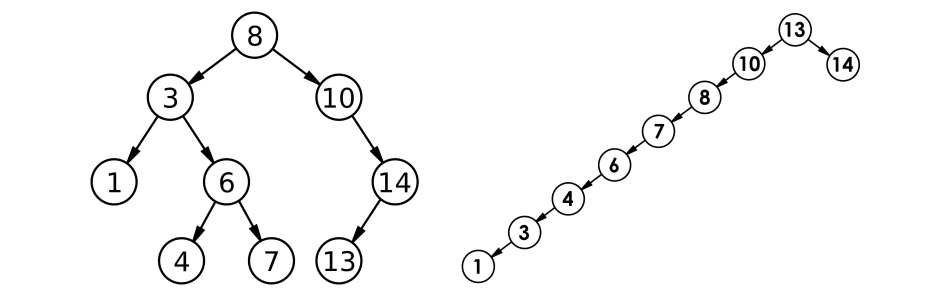
image.png

  • 最优情况：为完全二叉树 或 满二叉树时，O(n) = longn 。
  • 最坏情况：为单支树时，O(n) = n = 高度。

二叉树进阶面试题

二叉树创建字符串

https://leetcode.cn/problems/construct-string-from-binary-tree/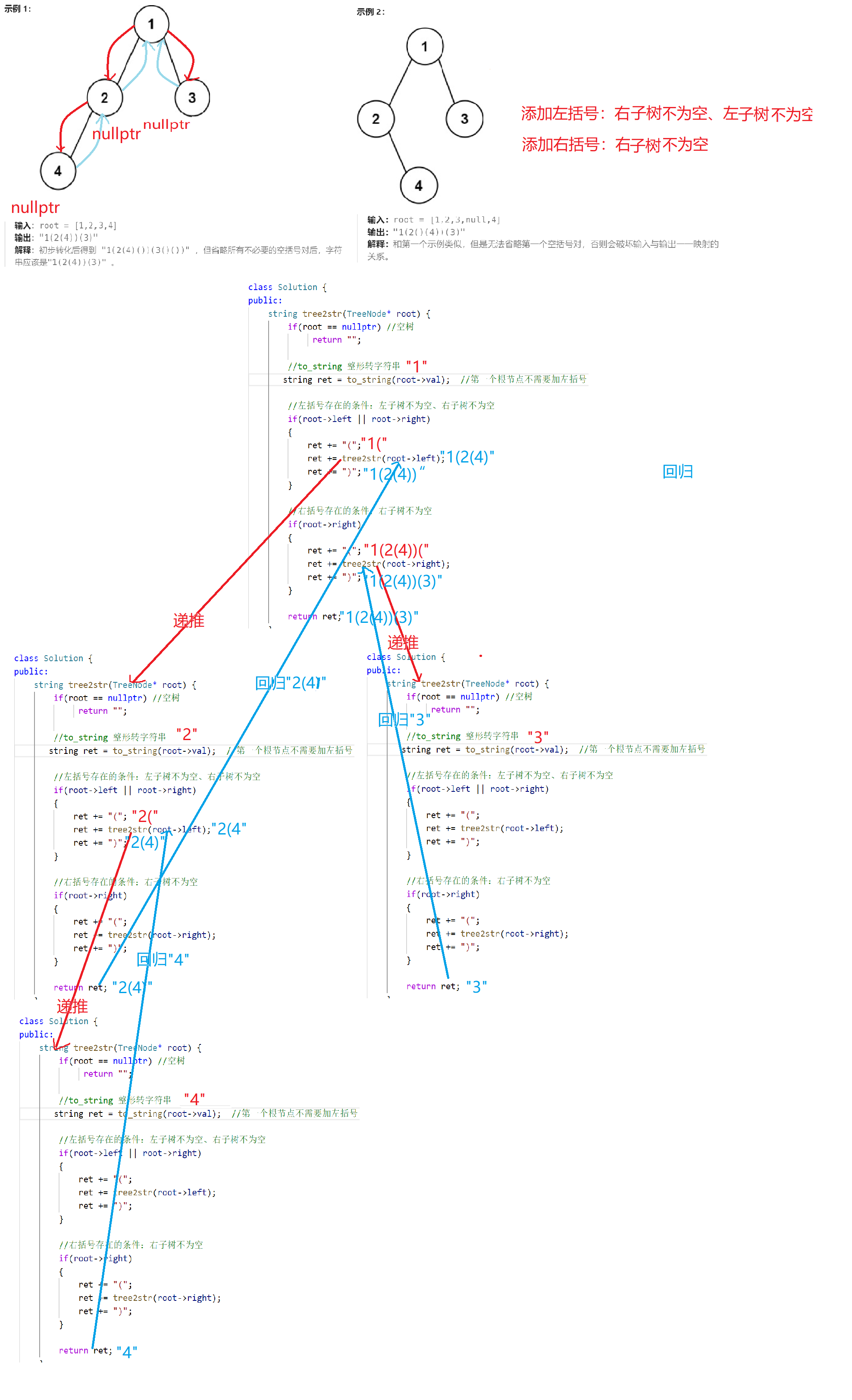
根据前序创建树.png

class Solution {
public:string tree2str(TreeNode* root) {if(root == nullptr) //空树return "";//to_string 整形转字符串string ret = to_string(root->val);  //第一个根节点不需要加左括号//左括号存在的条件：左子树不为空、右子树不为空if(root->left || root->right){ret += "(";ret += tree2str(root->left);ret += ")";}//右括号存在的条件：右子树不为空if(root->right){ret += "(";ret += tree2str(root->right);ret += ")";}return ret;}
};

二叉树的分层遍历I

https://leetcode.cn/problems/binary-tree-level-order-traversal/
层序遍历.gif.gif

class Solution {
public:vector<vector<int>> levelOrder(TreeNode* root) {vector<vector<int>> ret;int levesize = 0; //每层元素个数queue<TreeNode*> q; //队列，先进先出if(root) //第一个元素需要先入队列{q.push(root);levesize = 1;}while(!q.empty()){vector<int> v;while(levesize--)  //上一层出完，下一层的所有元素一定全部入队{TreeNode* tmp = q.front();q.pop();v.push_back(tmp->val);if(tmp->left)  q.push(tmp->left);if(tmp->right)q.push(tmp->right);}levesize = q.size();ret.push_back(v);}return ret;}
};

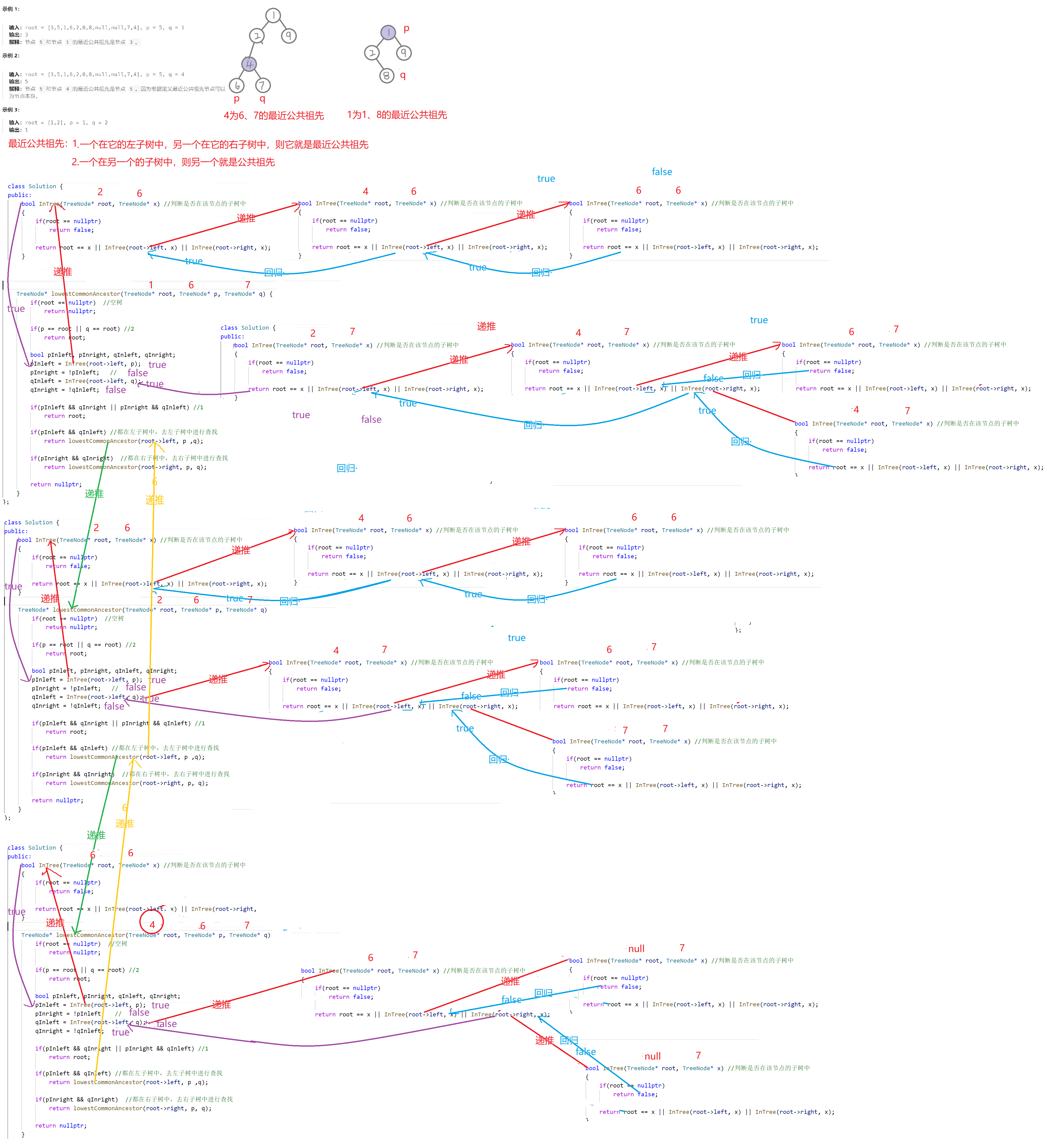
最近公共祖先

https://leetcode.cn/problems/lowest-common-ancestor-of-a-binary-tree/

/*最近公共祖先：1.一个为它的左子树、另一个为它的右子树。2.一个在它的子树中。最坏情况：O(n^2)*/
class Solution {
public:bool InTree(TreeNode* root, TreeNode* x) //判断是否在该节点的子树中{if(root == nullptr)return false;return root == x || InTree(root->left, x) || InTree(root->right, x);}TreeNode* lowestCommonAncestor(TreeNode* root, TreeNode* p, TreeNode* q) {if(root == nullptr)  //空树return nullptr;if(p == root || q == root) //2return root;bool pInleft, pInright, qInleft, qInright;pInleft = InTree(root->left, p);pInright = !pInleft;   //qInleft = InTree(root->left, q);qInright = !qInleft;if(pInleft && qInright || pInright && qInleft) //1return root;if(pInleft && qInleft) //都在左子树中，去左子树中进行查找return lowestCommonAncestor(root->left, p ,q);if(pInright && qInright)  //都在右子树中，去右子树中进行查找return lowestCommonAncestor(root->right, p, q);return nullptr;}
};

最近公共祖先.png

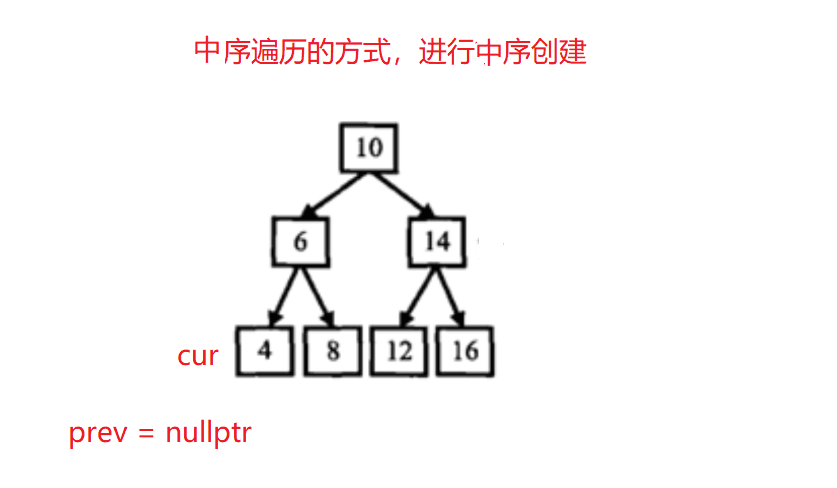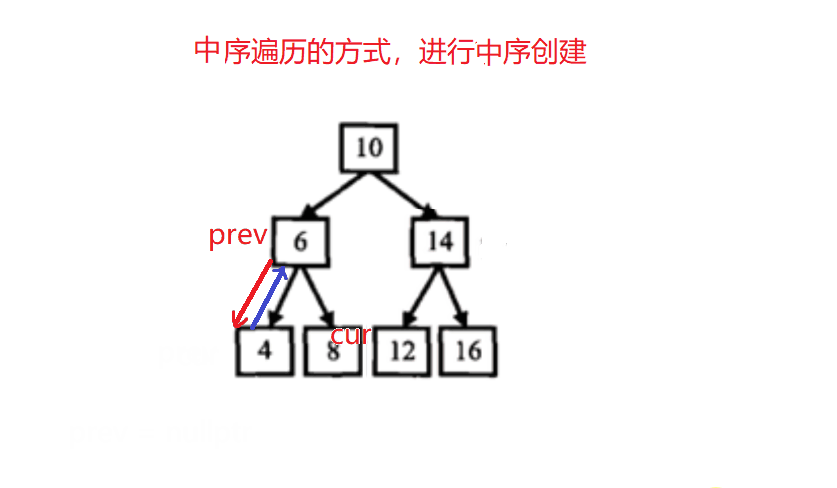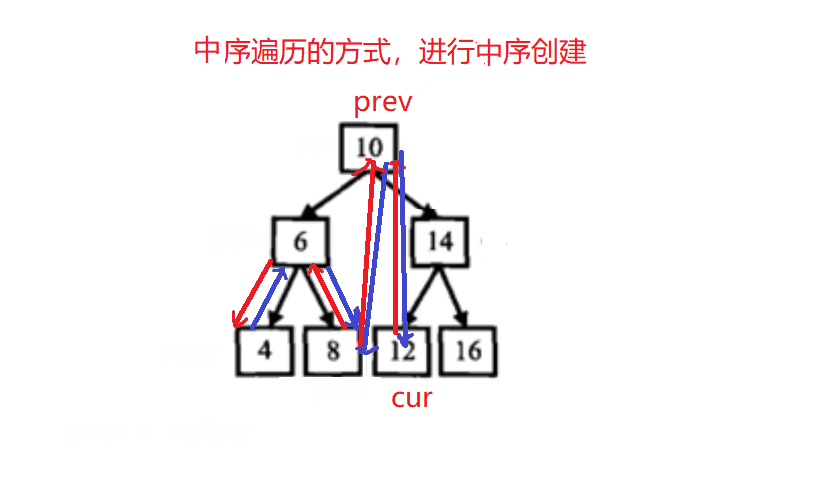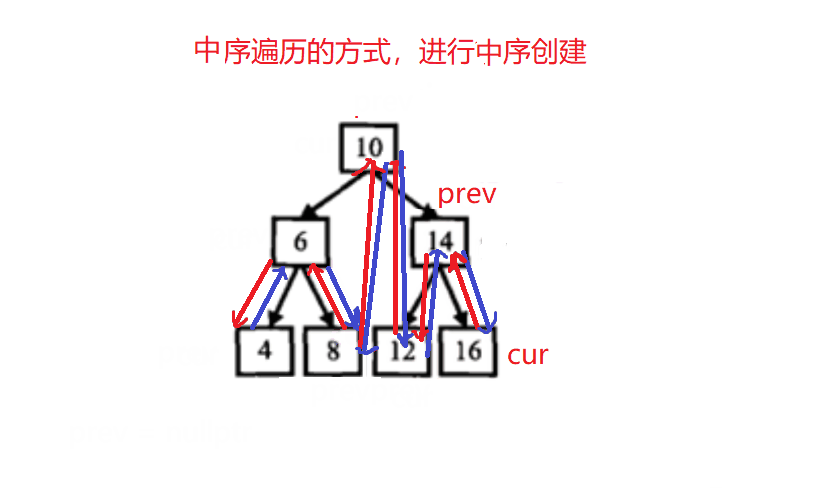
二叉搜索树与双向链表

https://www.nowcoder.com/share/jump/3163217841710348438605

class Solution {  //以中序遍历的方式，进行中序的创建
public:void _Convert(TreeNode* cur, TreeNode*& prev) //引用：变量在当前当栈帧的值，在其他栈帧仍保留{if(cur == nullptr) return ;_Convert(cur->left, prev); //左if(prev){   cur->left = prev; //当前节点的左指向前一个prev->right = cur; //前一个节点的右指向当前节点}prev = cur;  _Convert(cur->right, prev);  //右}TreeNode* Convert(TreeNode* pRootOfTree) {if(pRootOfTree == nullptr)return nullptr;TreeNode* prev = nullptr;_Convert(pRootOfTree, prev);while(pRootOfTree->left){pRootOfTree = pRootOfTree->left;}return pRootOfTree;}
};

二叉搜索树与双向链表.gif.gif

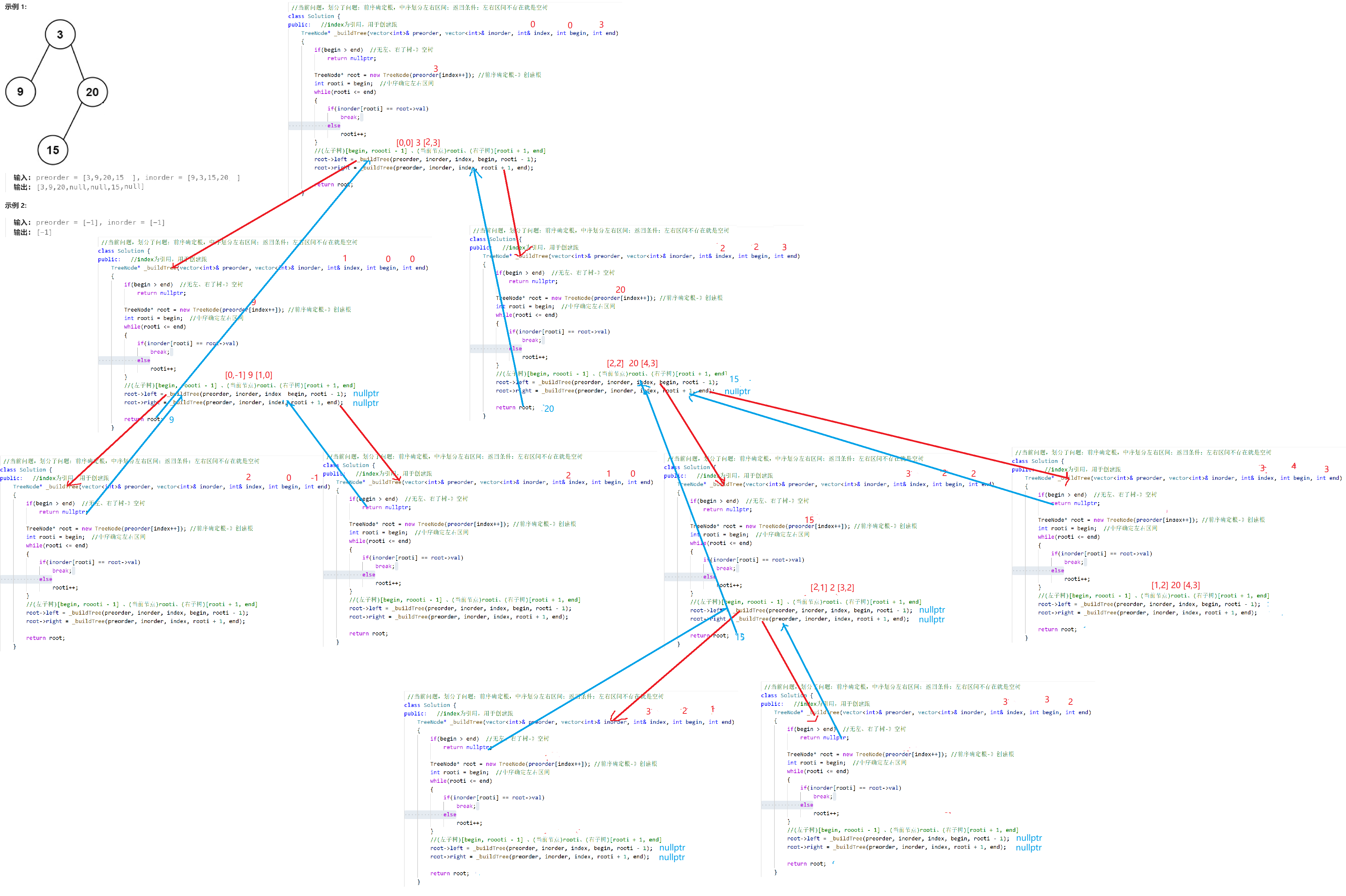
前序遍历与中序遍历构造二叉树

https://leetcode.cn/problems/construct-binary-tree-from-preorder-and-inorder-traversal/

//当前问题，划分子问题：前序确定根，中序划分左右区间；返回条件：左右区间不存在就是空树
class Solution {
public:   //index为引用，用于创建跟TreeNode* _buildTree(vector<int>& preorder, vector<int>& inorder, int& index, int begin, int end){if(begin > end)  //无左、右子树-》空树return nullptr; TreeNode* root = new TreeNode(preorder[index++]); //前序确定根-》创建根int rooti = begin;  //中序确定左右区间while(rooti <= end){if(inorder[rooti] == root->val)break;elserooti++;}//(左子树)[begin, roooti - 1] 、(当前节点)rooti、(右子树)[rooti + 1, end]root->left = _buildTree(preorder, inorder, index, begin, rooti - 1); root->right = _buildTree(preorder, inorder, index, rooti + 1, end); return root;}TreeNode* buildTree(vector<int>& preorder, vector<int>& inorder) {int index = 0;TreeNode* root = _buildTree(preorder, inorder, index, 0, inorder.size() - 1);return root;}
};

前中序创建树.png

中序遍历与后序遍历构造二叉树

https://leetcode.cn/problems/construct-binary-tree-from-inorder-and-postorder-traversal/

//中序(左、根、右):划分左右区间，后序(左、右、根)：从后往前依次是根、右子树的根、左子树的根
class Solution {
public:TreeNode* _bulidTree(vector<int>& inorder, vector<int>& postorder, int& prev, int begin, int end){if(begin > end)  //区间不存在，空树return nullptr;TreeNode* root = new TreeNode(postorder[prev--]); int rooti = begin;while(rooti <= end){if(inorder[rooti] == root->val)break;elserooti++;}root->right = _bulidTree(inorder, postorder, prev, rooti + 1, end); root->left = _bulidTree(inorder, postorder, prev, begin, rooti - 1);return root;}TreeNode* buildTree(vector<int>& inorder, vector<int>& postorder) {int prev = postorder.size() - 1;TreeNode* root = _bulidTree(inorder, postorder, prev, 0, inorder.size() - 1);return root;}
};

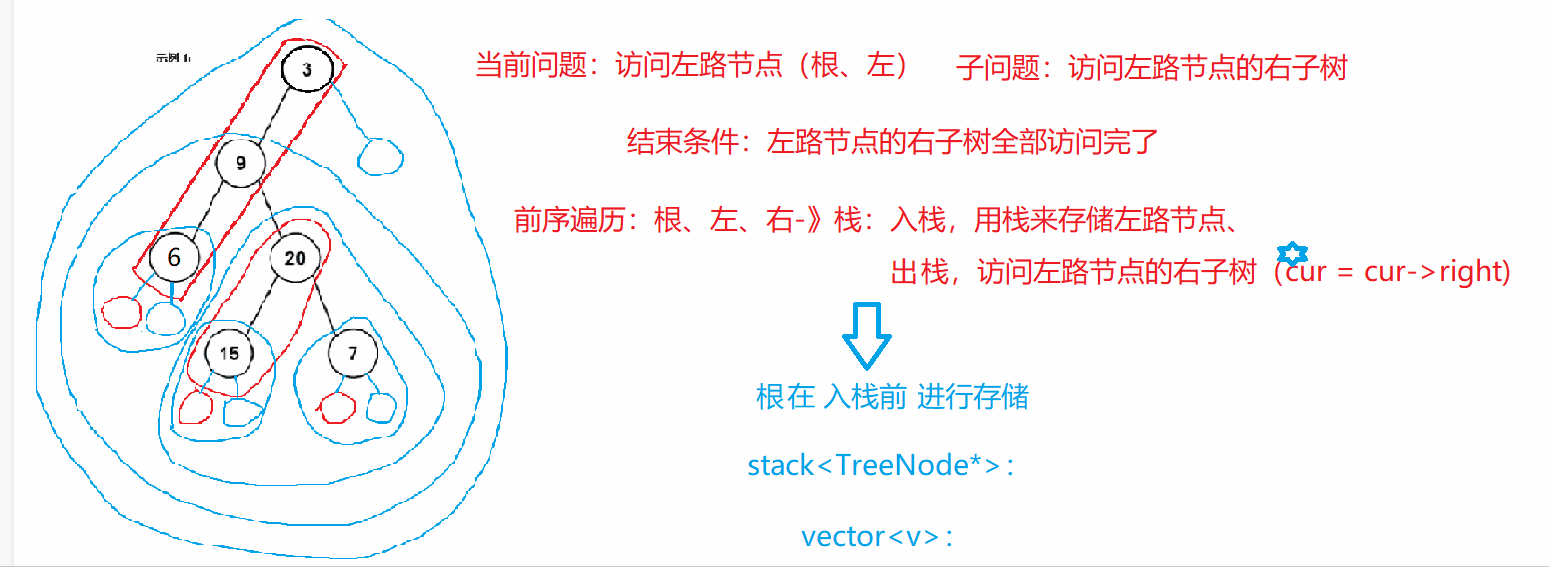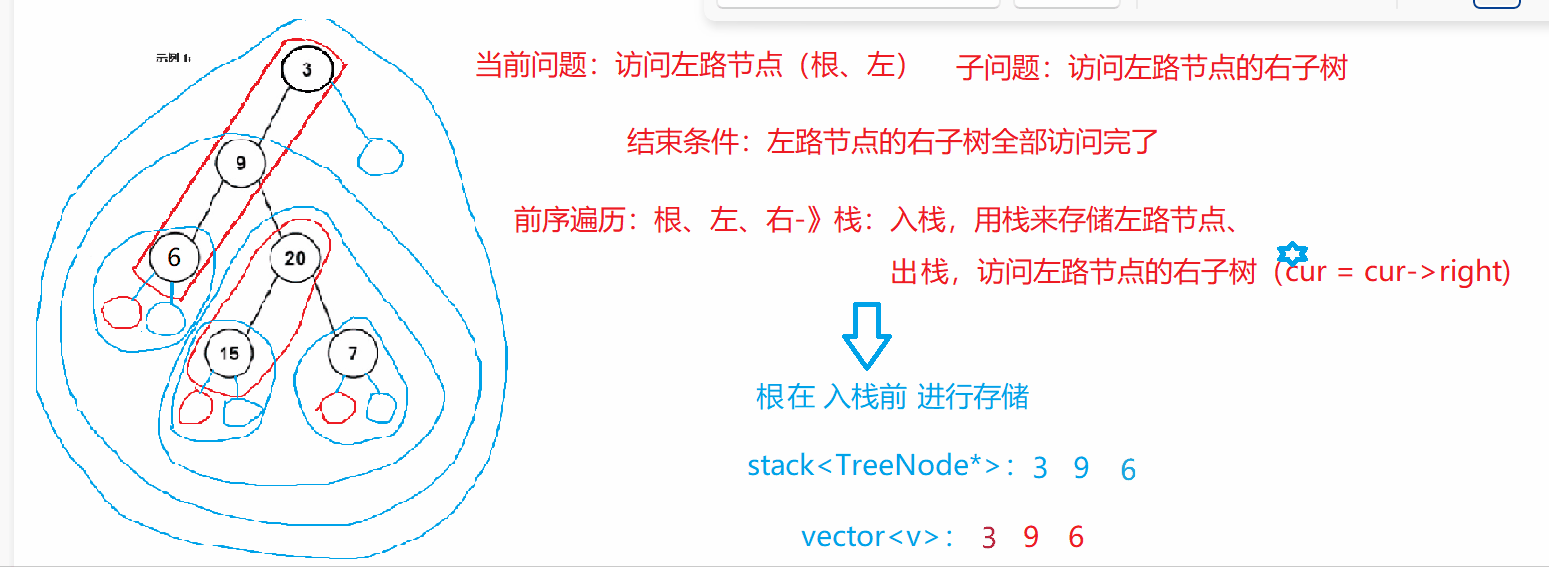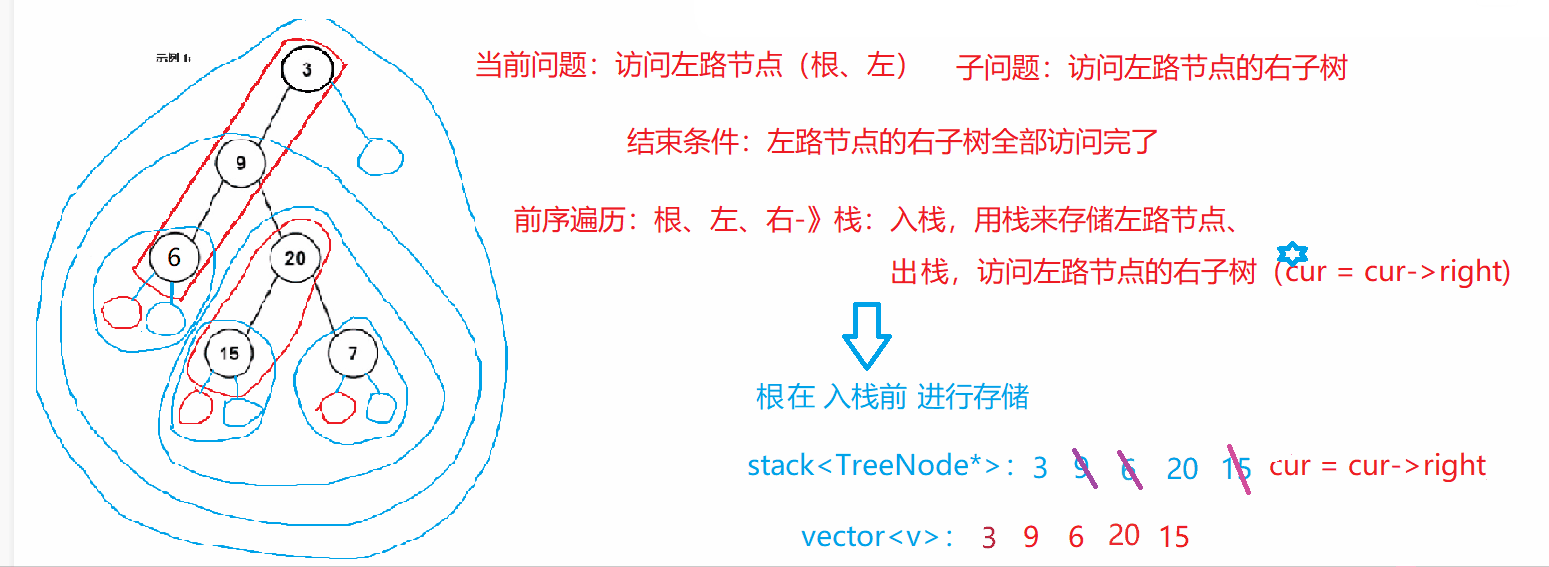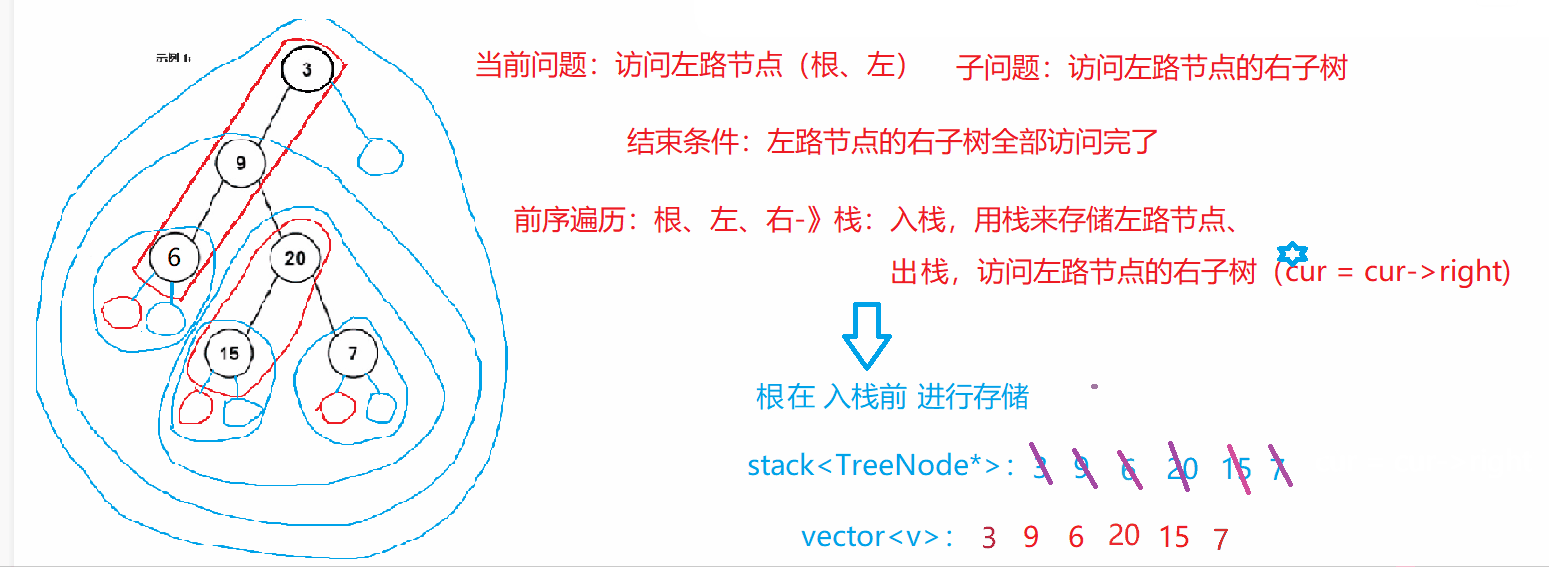
二叉树的前序遍历(非递归)

https://leetcode.cn/problems/binary-tree-preorder-traversal/

class Solution {
/*前序遍历(根、左、右)：当前问题：访问左路节点(根、左)，子问题：访问左路节点的右子树(右)
结束条件：左路节点的右树全部访问完*/
public:vector<int> preorderTraversal(TreeNode* root) {vector<int> v;  stack<TreeNode*> st;  //存储左路节点，栈中有剩余表示还有节点的右子树未访问TreeNode* cur = root;  //cur指向谁，表示访问那棵树的开始while(cur || !st.empty()) //结束条件，二者缺一不可{while(cur)  //访问左路节点{v.push_back(cur->val); //入栈前先"访问"根st.push(cur);cur = cur->left;}TreeNode* tmp = st.top(); st.pop();cur = tmp->right;  //访问左路节点的右子树——子问题}return v;}
};

前序遍历（非递归）.gif.gif

二叉树的中序遍历(非递归)

https://leetcode.cn/problems/binary-tree-inorder-traversal/

//与前序遍历相同，唯一不同的是：根在出栈后进行存储
class Solution {
public:vector<int> inorderTraversal(TreeNode* root) {vector<int> v;stack<TreeNode*> st;TreeNode* cur = root;while(cur || !st.empty()){while(cur){st.push(cur);cur = cur->left;}TreeNode* tmp = st.top();st.pop();v.push_back(tmp->val);cur = tmp->right;}return v;}
};

二叉树的后序遍历(非递归)

https://leetcode.cn/problems/binary-tree-postorder-traversal/

class Solution {
public:vector<int> postorderTraversal(TreeNode* root) {vector<int> v;stack<TreeNode*> st;  TreeNode* cur = root;TreeNode* prev = nullptr; //记录被访问的前一个节点while(cur || !st.empty()){while(cur) //访问左路节点{st.push(cur);cur = cur->left;}TreeNode* tmp = st.top(); //表示tmp节点的左子树已经访问完了/*1.当前节点的右子树为空 或者 当前节点的右子树为上一个被访问的节点2.否则，就子问题访问当前节点的右子树*/if(tmp->right == nullptr || prev == tmp->right){st.pop();v.push_back(tmp->val);prev = tmp;}else  {cur = tmp->right;}/*注意：else不能省略，结果有误，因为根节点是最后进行删除的，若此时根节点已经删除，cur=tmp->right,尽管栈已经pop为空栈了，但只是删除了树节点的指针，树的结点仍存在，导致继续访问2、3，直到cur为空，最终结果就为[3, 2, 1, 3, 1]*/}return v;}
};

http://www.ppmy.cn/news/1452761.html

相关文章

面试题分享之Java集合篇（三）

面试题分享之Java集合篇（三）

注意&#xff1a;文章若有错误的地方&#xff0c;欢迎评论区里面指正 &#x1f36d; 系列文章目录 面试题分享之Java基础篇&#xff08;二&#xff09;面试题分享之Java基础篇&#xff08;三&#xff09; 面试题分享之Java集合篇&#xff08;一&#xff09;、 面试题分享之Ja…
阅读更多...
【代码随想录】day48

【代码随想录】day48

提示&#xff1a;文章写完后&#xff0c;目录可以自动生成&#xff0c;如何生成可参考右边的帮助文档 文章目录 一、198打家劫舍二、213打家劫舍II三、337打家劫舍III 一、198打家劫舍 class Solution { public:int rob(vector<int>& nums) {vector<int> dp(n…
阅读更多...
JET毛选学习笔记：如何利用《矛盾论》从做实验到做科研vol. 2

JET毛选学习笔记：如何利用《矛盾论》从做实验到做科研vol. 2

上一节讲完矛盾的普遍性和特殊性都已经5000字了&#xff0c;为了不影响阅读观感&#xff08;多水几篇&#xff09;&#xff0c;把他们进行了拆分&#xff0c;那我就继续侃大山吧。 五、矛盾的同一性和斗争性 先做名词解释&#xff1a; 矛盾的同一性&#xff08;统一&#xf…
阅读更多...
neo4j 的插入速度为什么越来越慢，可能是使用了过多图谱查询操作

neo4j 的插入速度为什么越来越慢，可能是使用了过多图谱查询操作

文章目录 背景描述分析解决代码参考neo4j 工具类Neo4jDriver知识图谱构建效果GuihuaNeo4jClass 背景描述 使用 tqdm 显示&#xff0c;处理的速度&#xff1b; 笔者使用 py2neo库&#xff0c;调用 neo4j 的API 完成节点插入&#xff1b; 有80万条数据需要插入到neo4j图数据中&am…
阅读更多...
[Linux][守护进程]详细讲解 + 自主实现

[Linux][守护进程]详细讲解 + 自主实现

目录 0.预备知识1.守护进程概念2.进程组概念3.会话概念4.守护进程化的方式5.实现daemon() 0.预备知识 **前台进程&#xff1a;**和终端关联的进程任何一次会话&#xff0c;只允许有一个前台进程和多个后台进程守护进程不能直接向显示器打印消息&#xff0c;一旦打印&#xff0…
阅读更多...
爱已无可救药

爱已无可救药

【爱的极限挑战】《爱已无可救药》—— 破晓前最暗的夜&#xff0c;恋人间最深的痴迷 在这个信息爆炸的时代&#xff0c;爱情故事千千万&#xff0c;但真正能触达心灵深处的&#xff0c;寥若晨星。《爱已无可救药》这部短剧&#xff0c;如同夜空中最耀眼的流星&#xff0c;划破…
阅读更多...
Sqli-labs第一关到第四关

Sqli-labs第一关到第四关

目录 一&#xff0c;了解PHP源代码 二&#xff0c;破解第一关 2.1在了解完源码之后&#xff0c;我们重点看一下 2.2破解这道题表中有几列 2.3查看表中哪一列有回显 2.4查询库&#xff0c;表&#xff0c;列信息 三&#xff0c;总结 前提&#xff1a; 之所以把1234关…
阅读更多...
【算法系列】哈希表

【算法系列】哈希表

目录 哈希表总结 leetcode题目 一、两数之和 二、判定是否互为字符重排 三、存在重复元素 四、存在重复元素 II 五、字母异位词分组 六、在长度2N的数组中找出重复N次的元素 七、两个数组的交集 八、两个数组的交集 II 九、两句话中的不常见单词 哈希表总结 1.存储数…
阅读更多...
最新文章

Copyright @ 2022~2023