首先,这是一个基于柯尔莫哥洛夫-阿诺德表示定理的网络。这个定理指出如果函数f是定义在有界域上的多变量连续函数(即最终要拟合的非线性函数是连续的),那么该函数就可以表示为多个单变量、加法连续函数的有线组合。
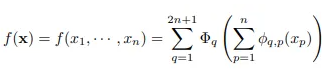
对于机器学习来说,KAN网络的基础是学习高维函数的过程可以简化成学习多项式数量的一维函数。
其次,这个网络与多层感知机MLP的不同在于,直观上激活函数在MLP的神经元节点上,而激活函数(用B样条曲线来参数化)在KAN的边权上。换句话说,MLP的激活函数相同,靠边权不同来学习。KAN的激活函数本就不相同。因此KAN具有更少的参数和更强的可解释性。
最后,KAN网络的深度和宽度取决于复合函数(即堆叠KAN层的设计)。其中每个层都是由但变量函数组成,因此可以对函数进行单独学习和理解。——先单独激活再求和,记作一个单变量函数
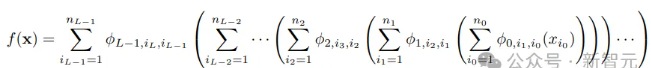
其中单变量函数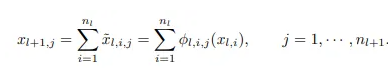
而MLP则是——先求和再一起激活,更新神经元
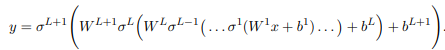
小结
KAN相比MLP具有以下优点:
1.持续性学习。不会发生灾难性遗忘(由于B样条参数化激活函数)
2.具有更好的帕累托前沿。指资源分配最优的理想状态。
3.可解释性。可以输出激活函数的数学化表示(小样本合成数据集上已验证)——适合解耦强的问题,那如果两个变量乘积影响y还适用不?