【LeetCode】拓扑排序—

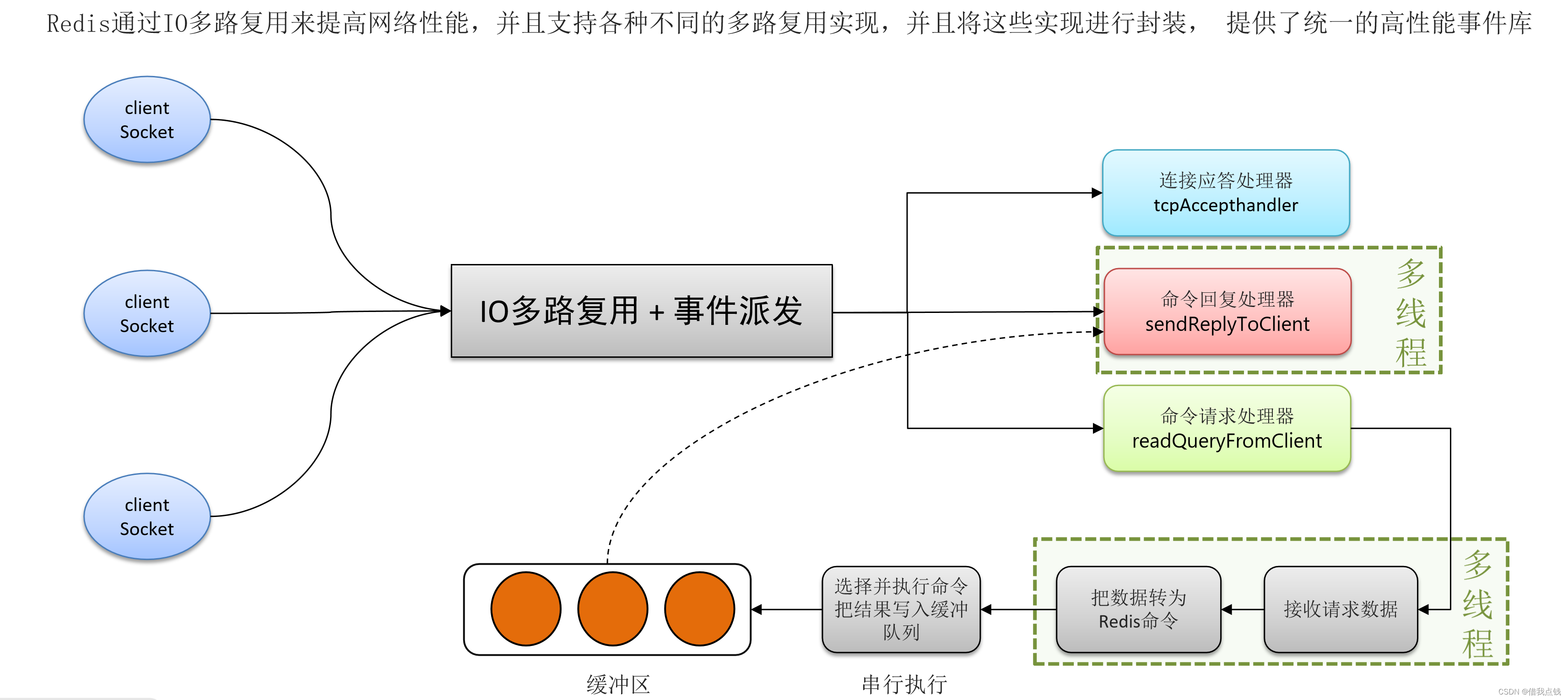
拓扑排序：

AOV网：若用DAG图（有向无环图）表示一个工程，其顶点表示活动，用有向边<Vi, Vj>表示活动Vi必须先于活动Vj进行的这样一种关系，则将这种有向图称为顶点表示活动的网络，记为AOV网。在AOV网中，活动Vi是活动Vj的直接前驱，活动Vj是活动Vi的直接后继，这种前驱和后继关系具有传递性，且任何活动Vi不能以它自己作为自己的前驱或后继。

拓扑排序：在图论中，由一个有向无环图的顶点组成的序列，当且仅当满足下列条件时，称为该图的一个拓扑排序：

每个顶点出现且只出现一次。
若顶点A在序列中排在顶点B的前面，则在图中不存在从顶点B到顶点A的路径。

或定义为：拓扑排序是对有向无环图的顶点的一种排序，它使得若存在一条从顶点A到顶点B的路径，则在排序中顶点B出现在顶点A的后面。每个AOV网都有一个或多个拓扑排序序列。

对一个AOV网进行拓扑排序的算法有很多，下面介绍比较常用的一种方法的步骤：

从AOV网中选择一个没有前驱的顶点并输出。
从网中删除该顶点和所有以它为起点的有向边。
重复①和②直到当前的AOV网为空或当前网中不存在无前驱的顶点为止。后一种情况说明有向图中必然存在环。

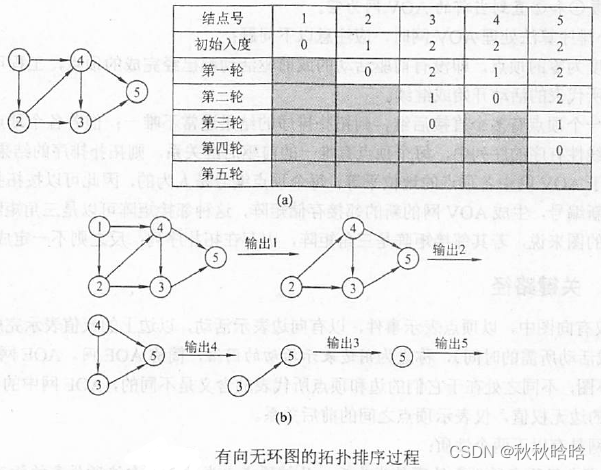
如图所示为拓扑排序过程的示例。每轮选择一个入度为0的顶点并输出，然后删除该顶点和所有以它为起点的有向边，最后得到拓扑排序的结果为{1, 2, 4, 3, 5}。

实现拓扑排序：借助队列，来一次BFS

初始化：把所有入度为0的顶点加入到队列中
当队列不为空的时候
1）拿出队头元素，加入到最终结果中
2）删除与该元素相连的边
3）判断与删除边相连的顶点是否入度变成0，变成0则加入到队列中

图的存储之邻接表法：

当一个图为稀疏图时，使用邻接矩阵法显然要浪费大量的存储空间，而图的邻接表法结合了顺序存储和链式存储方法，大大减少了这种不必要的浪费。

所谓邻接表，是指对图G中的每个顶点Vi建立一个单链表，第i个单链表中的结点表示依附于顶点Vi的边（对于有向图则是以顶点Vi为尾的弧），这个单链表就为顶点Vi的边表（对于有向图则称为出边表）。边表的头指针和顶点的数据信息采用顺序存储（称为顶点表），所以在邻接表中存在两种结点：顶点表结点和边表结点，如图所示。

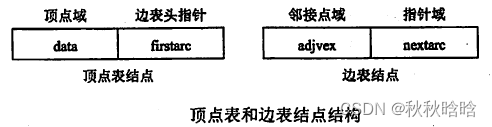
顶点表结点由顶点域(data)和指向第一条邻接边的指针(firstarc)构成，边表（邻接表）结点由邻接点域(adjvex)和指向下一条邻接边的指针域(nextarc)构成。

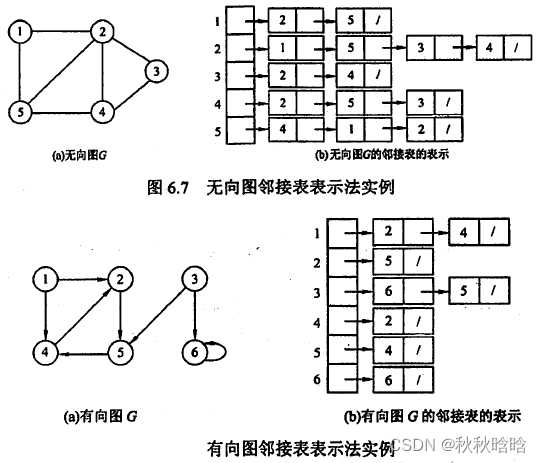
无向图和有向图的邻接表的实例如图所示。

两种表示方法：

vector<vector<int>> edges
unordered_map<int, vector<int>> edges

根据题目需要可以把int换成string。

1. 课程表（中等）

class Solution {
public:bool canFinish(int numCourses, vector<vector<int>>& prerequisites) {// 1. 准备工作unordered_map<int, vector<int>> edges; // 邻接表存图vector<int> in(numCourses); // 标记每一个顶点的入度// 2. 建图for (auto& e : prerequisites){int a = e[0], b = e[1]; // b->a的一条边edges[b].push_back(a);in[a]++;}// 3. 拓扑排序queue<int> q;// (1) 把所有入度为0的点加入到队列中for (int i = 0; i < numCourses; i++){if (in[i] == 0){q.push(i);}}// (2) BFSwhile(!q.empty()){int cur = q.front();q.pop();for (auto& a : edges[cur]){in[a]--;if (in[a] == 0){q.push(a);}}}// 4. 判断是否有环for (int i = 0; i < numCourses; i++){if (in[i])return false;}return true;}
};

2. 课程表 II（中等）

class Solution {
public:vector<int> findOrder(int numCourses, vector<vector<int>>& prerequisites) {// 1. 准备工作vector<vector<int>> edges(numCourses); // 邻接表存图vector<int> in(numCourses); // 标记每一个顶点的入度// 2. 建图for (auto& e : prerequisites){int a = e[0], b = e[1]; // b->a的一条边edges[b].push_back(a);in[a]++;}// 3. 拓扑排序queue<int> q;vector<int> ans;// (1) 把所有入度为0的点加入到队列中for (int i = 0; i < numCourses; i++){if (in[i] == 0){q.push(i);}}// (2) BFSwhile(!q.empty()){int cur = q.front();q.pop();ans.push_back(cur);for (auto& a : edges[cur]){in[a]--;if (in[a] == 0){q.push(a);}}}// 4. 判断是否有环if (ans.size() == numCourses)return ans;return {};}
};