踏上R语言之旅：解锁数据世界的神秘密码（四）

文章目录

前言
一、多元线性回归
- 1.多元线性回归模型的建立
- 2.多元线性回归模型的检验
二、多元线性相关分析
- 1.矩阵相关分析
- 2.复相关分析
三、回归变量的选择方法
- 1.变量选择准则
- 2.变量选择的常用准则
- 3.逐步回归分析
总结

前言

回归分析研究的主要对象是客观事物变量间的统计关系。它是建立在对客观事物进行大量实验和观察的基础上，用来寻找隐藏在看起来不确定的现象中的统计规律的统计方法。它与相关分析的主要区别为：
一是在回归分析中，解释变量称为自变量，被解释变量称为因变量，处于被解释的特殊地位；而在相关分析中，并不区分自变量和因变量，各变量处于平等地位。
二是在相关分析中所涉及的变量全是随机变量；而在回归分析中，只有因变量是随机变量，自变量可以是随机变量，也可以是非随机变量。
三是相关分析研究主要是为刻画两类变量间的线性相关的密切程度；而回归分析不仅可以揭示自变量对因变量的影响大小，还可以由回归方程进行预测和控制。

一、多元线性回归

1.多元线性回归模型的建立

1.一般形式：
![](https://img-blog.csdnimg.cn/direct/378e658764c64831a00b57bcd33cf93b.png)
当得到n组数据时，
在这里插入图片描述
2.线性回归模型的基本假设

3.多元回归参数的最小二乘估计

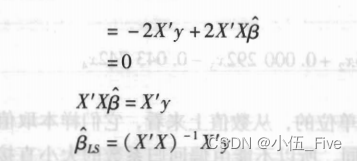
例.财政收入多元分析

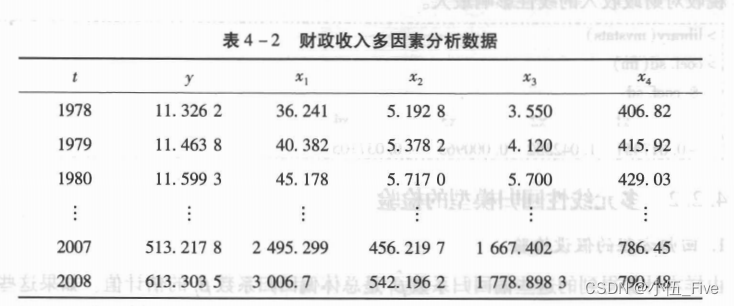
> yX=read.table("clipboard",header=T)
> plot(yX,gap=0)

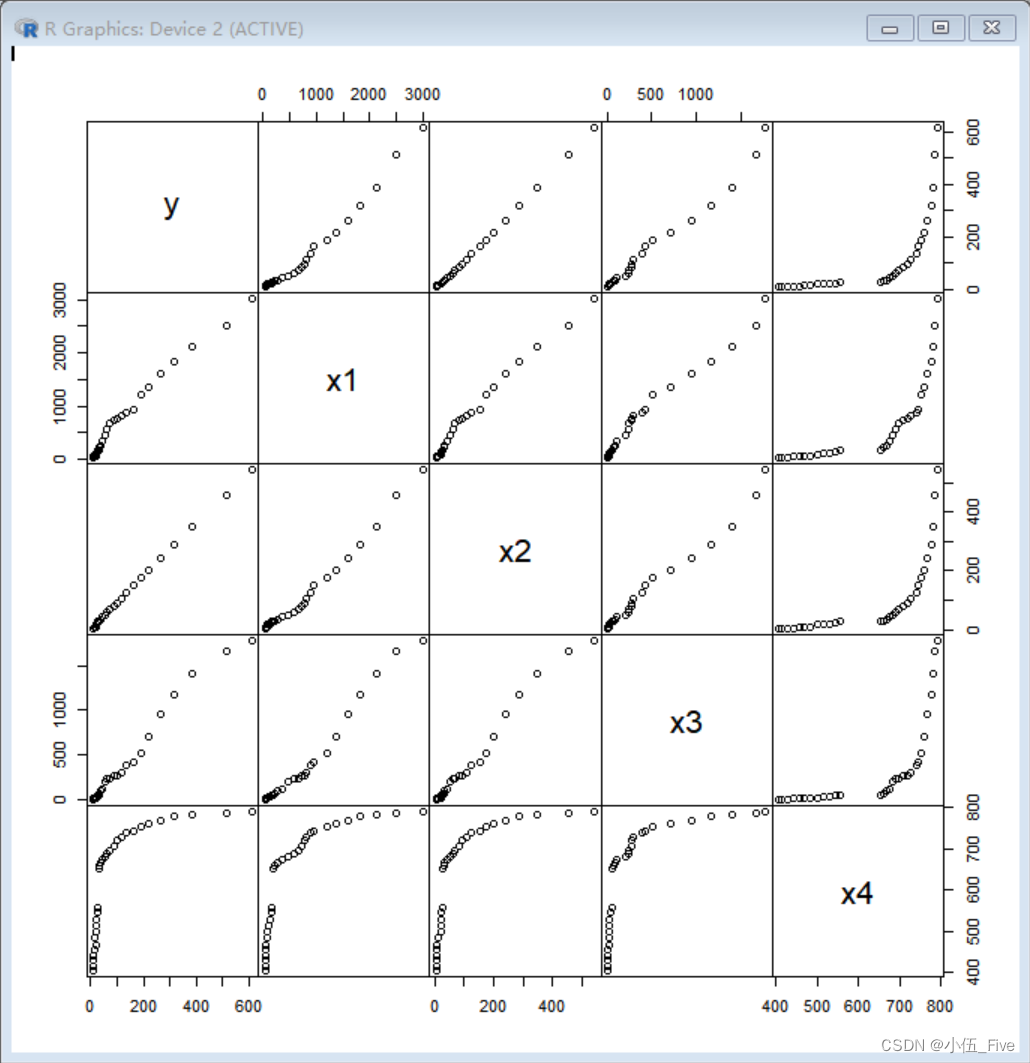
在这里插入图片描述

> (fm=lm(y~x1+x2+x3+x4,data=yX))#显示多元线性回归模型Call:
lm(formula = y ~ x1 + x2 + x3 + x4, data = yX)Coefficients:
(Intercept)           x1           x2           x3           x4  23.5321088   -0.0033866    1.1641150    0.0002919   -0.0437416

4.标准化偏回归系数
在这里插入图片描述
标准化偏回归系数：

> coef.sd(fm)#标准化偏回归系数结果
$coef.sdx1            x2            x3            x4 
-0.0174513678  1.0423522972  0.0009628564 -0.0371053994

2.多元线性回归模型的检验

1.回归方程的假设检验
在这里插入图片描述

2.回归系数的假设检验

> anova(fm)#多元线性回归模型方差分析
Analysis of Variance TableResponse: yDf Sum Sq Mean Sq    F value    Pr(>F)    
x1         1 694627  694627 89259.0016 < 2.2e-16 ***
x2         1  17803   17803  2287.6286 < 2.2e-16 ***
x3         1     24      24     3.0569    0.0922 .  
x4         1    174     174    22.2954 7.005e-05 ***
Residuals 26    202       8                         
---
Signif. codes:  0 ‘***’ 0.001 ‘**’ 0.01 ‘*’ 0.05 ‘.’ 0.1 ‘ ’ 1

P<0.0001 则本例回归模型有意义
接下来进行参数估计及检验：

> summary(fm)#多元线性回归系数t检验Call:
lm(formula = y ~ x1 + x2 + x3 + x4, data = yX)Residuals:Min      1Q  Median      3Q     Max 
-5.0229 -2.1354  0.3297  1.2639  6.9690 Coefficients:Estimate Std. Error t value Pr(>|t|)    
(Intercept) 23.5321088  4.5990714   5.117 2.47e-05 ***
x1          -0.0033866  0.0080749  -0.419    0.678    
x2           1.1641150  0.0404889  28.751  < 2e-16 ***
x3           0.0002919  0.0085527   0.034    0.973    
x4          -0.0437416  0.0092638  -4.722 7.00e-05 ***
---
Signif. codes:  0 ‘***’ 0.001 ‘**’ 0.01 ‘*’ 0.05 ‘.’ 0.1 ‘ ’ 1Residual standard error: 2.79 on 26 degrees of freedom
Multiple R-squared:  0.9997,    Adjusted R-squared:  0.9997 
F-statistic: 2.289e+04 on 4 and 26 DF,  p-value: < 2.2e-16

由t检验结果可见，偏回归系数b2、b4的P值都小于0.01，可认为解释变量税收x2和经济活动人口x4显著；b1、b3的P值大于0.50，不能否定B1=0、B3=0的假设，可认为国内生产总
值x,和进出口贸易总额x3对财政收人y没有显著的影响。我们可以看到，国内生产总值、经济活动人口所对应的偏回归系数都为负，这与经济现实是不相符的。出现这种结果的可能原因是这些解释变量之间存在高度的共线性。

二、多元线性相关分析

在相关分析中，研究较多的是两个变量之间的关系，称为简单相关。当涉及的变量为三个或三个以上时，称为偏相关或复相关。实际上，偏相关（复相关）是对简单相关的一种推广。
在有些情况下，我们只想了解两变量之间有无线性相关关系，并不需要建立它们之间的回归模型，也不需要区分自变量和因变量，这时，就可用较为方便的相关分析方法。

1.矩阵相关分析

计算两两间的相关系数：

> cor(yX)#多元数据相关系数矩阵y        x1        x2        x3        x4
y  1.0000000 0.9871498 0.9994718 0.9912053 0.6956619
x1 0.9871498 1.0000000 0.9907018 0.9867664 0.7818066
x2 0.9994718 0.9907018 1.0000000 0.9917094 0.7154297
x3 0.9912053 0.9867664 0.9917094 1.0000000 0.7073820
x4 0.6956619 0.7818066 0.7154297 0.7073820 1.0000000

给出两两间的矩阵散点图：

pairs(x,…)
x为数值矩阵或数据框

> pairs(yX)#多元数据散点

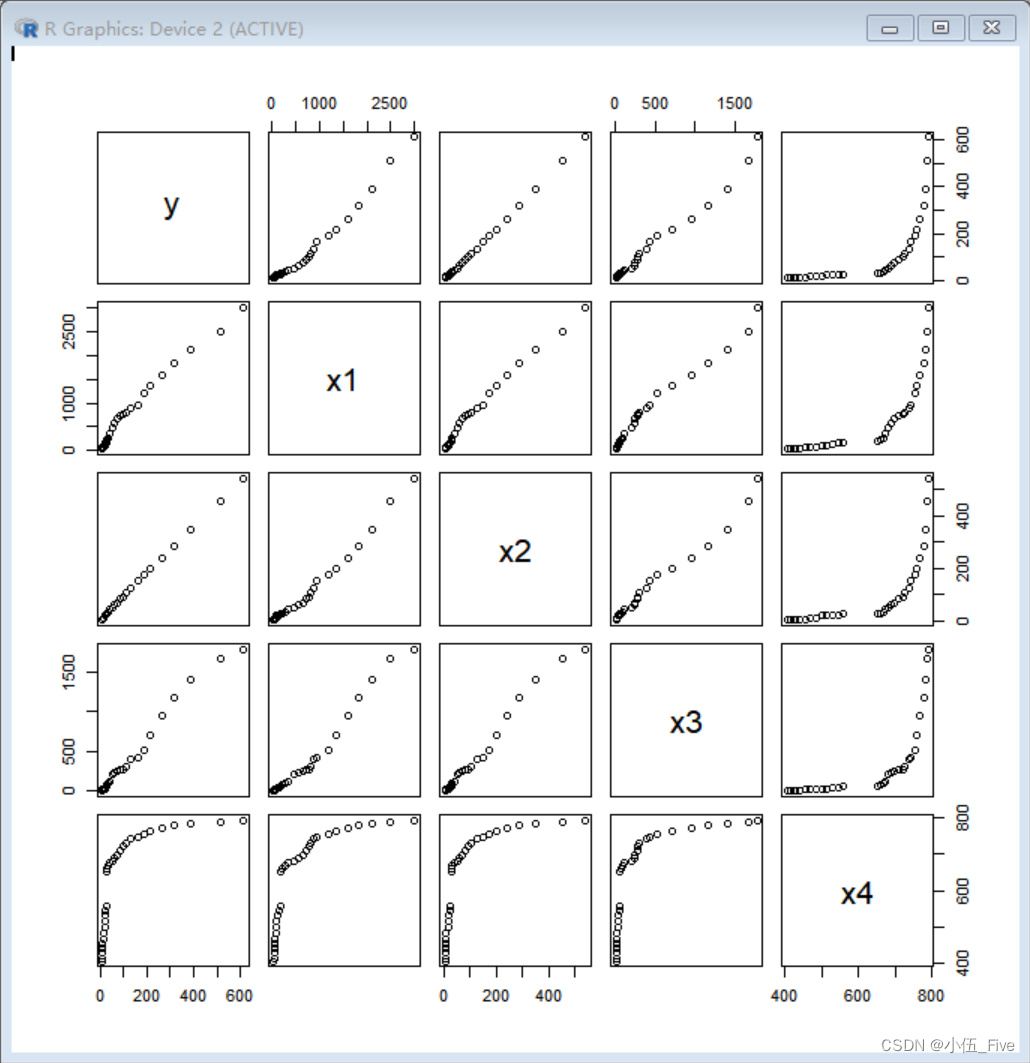
在这里插入图片描述
假设检验：

> corr.test(yX)#多元数据相关系数检验
corr test: y     x1     x2    x3 x4
y    0.000  0.000  0.000 0.000  0
x1  33.267  0.000  0.000 0.000  0
x2 165.614 39.214  0.000 0.000  0
x3  40.336 32.772 41.560 0.000  0
x4   5.215  6.752  5.514 5.389  0
lower is t value，upper is p value

2.复相关分析

1.复相关系数的计算
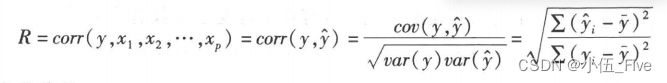
在这里插入图片描述
2.决定系数

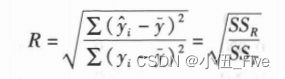
> (R2=summary(fm)$r.sq)#显示多元线性回归模型决定系数
[1] 0.9997
> (R=sqrt(R2))#显示多元数据复相关系数
[1] 0.9999

三、回归变量的选择方法

1.变量选择准则

一、全局择优法

> install.packages("leaps")
--- 在此連線階段时请选用CRAN的鏡子 ---
试开URL’https://cloud.r-project.org/bin/windows/contrib/4.3/leaps_3.1.zip'
Content type 'application/zip' length 86995 bytes (84 KB)
downloaded 84 KB程序包‘leaps’打开成功，MD5和检查也通过下载的二进制程序包在C:\Users\86187\AppData\Local\Temp;\RtmpCeDQI1\downloaded_packages里
> library(leaps)#加载leaps包
Warning message:
程辑包‘leaps’是用R版本4.3.3 来建造的 
> varsel=regsubsets(y~x1+x2+x3+x4,data=yX)#多元数据线性回归变量选择模型
> result=summary(varsel)#变量选择方法结果  
> data.frame(result$outmat,RSS=result$rss,R2=result$rsq)#RSS和决定系数准则结果展示 x1 x2 x3 x4   RSS     R2
1  ( 1 )     *       752.9 0.9989
2  ( 1 )     *     * 203.9 0.9997
3  ( 1 )  *  *     * 202.3 0.9997
4  ( 1 )  *  *  *  * 202.3 0.9997

2.变量选择的常用准则

> data.frame(result$outmat,adjR2=result$adjr2,Cp=result$cp,BIC=result$bic)x1 x2 x3 x4  adjR2     Cp    BIC
1  ( 1 )     *       0.9989 69.745 -205.6
2  ( 1 )     *     * 0.9997  1.199 -242.6
3  ( 1 )  *  *     * 0.9997  3.001 -239.4
4  ( 1 )  *  *  *  * 0.9997  5.000 -236.0

3.逐步回归分析

1.向前引入法
2.向后剔除法
3.逐步筛选法
在这里插入图片描述

> fm.step=step(fm,direction="forward")#向前引入法变量选择结果
Start:  AIC=68.15
y ~ x1 + x2 + x3 + x4> fm.step=step(fm,direction="backward")#向后剔除法变量选择结果
Start:  AIC=68.15
y ~ x1 + x2 + x3 + x4Df Sum of Sq  RSS   AIC
- x3    1         0  202  66.2
- x1    1         1  204  66.4
<none>               202  68.2
- x4    1       174  376  85.4
- x2    1      6433 6635 174.4Step:  AIC=66.16
y ~ x1 + x2 + x4Df Sum of Sq  RSS   AIC
- x1    1         2  204  64.4
<none>               202  66.2
- x4    1       197  400  85.3
- x2    1      7382 7585 176.5Step:  AIC=64.39
y ~ x2 + x4Df Sum of Sq    RSS   AIC
<none>                 204  64.4
- x4    1       549    753 102.9
- x2    1    367655 367859 294.8
> fm.step=step(fm,direction="both")#逐步筛选法变量选择结果
Start:  AIC=68.15
y ~ x1 + x2 + x3 + x4Df Sum of Sq  RSS   AIC
- x3    1         0  202  66.2
- x1    1         1  204  66.4
<none>               202  68.2
- x4    1       174  376  85.4
- x2    1      6433 6635 174.4Step:  AIC=66.16
y ~ x1 + x2 + x4Df Sum of Sq  RSS   AIC
- x1    1         2  204  64.4
<none>               202  66.2
+ x3    1         0  202  68.2
- x4    1       197  400  85.3
- x2    1      7382 7585 176.5Step:  AIC=64.39
y ~ x2 + x4Df Sum of Sq    RSS   AIC
<none>                 204  64.4
+ x1    1         2    202  66.2
+ x3    1         0    204  66.4
- x4    1       549    753 102.9
- x2    1    367655 367859 294.8

总结

本节学习了多元回归分析以及逐步回归分析的基本解决步骤及方法，学到了很多，继续加油！