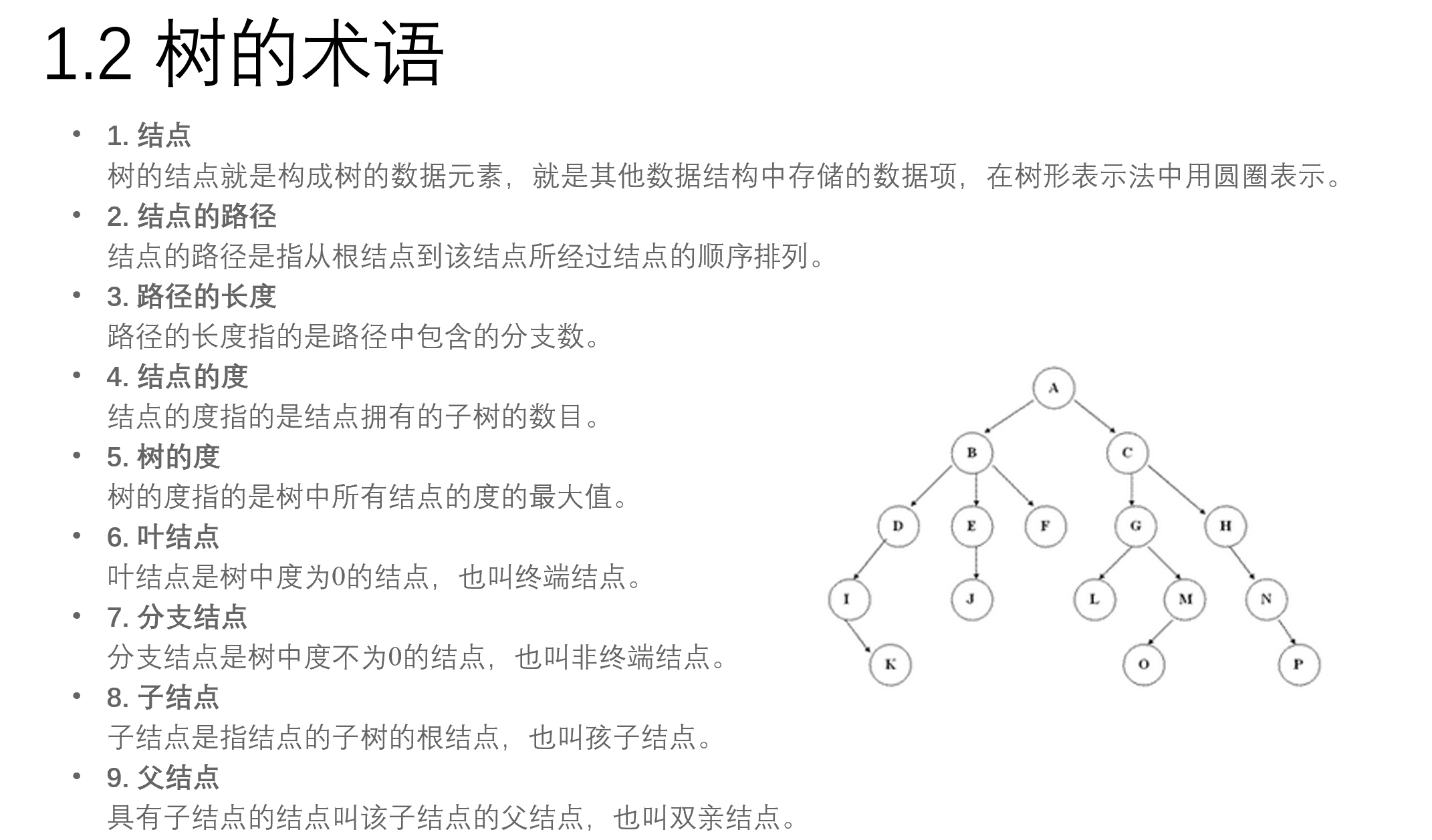
1. 树
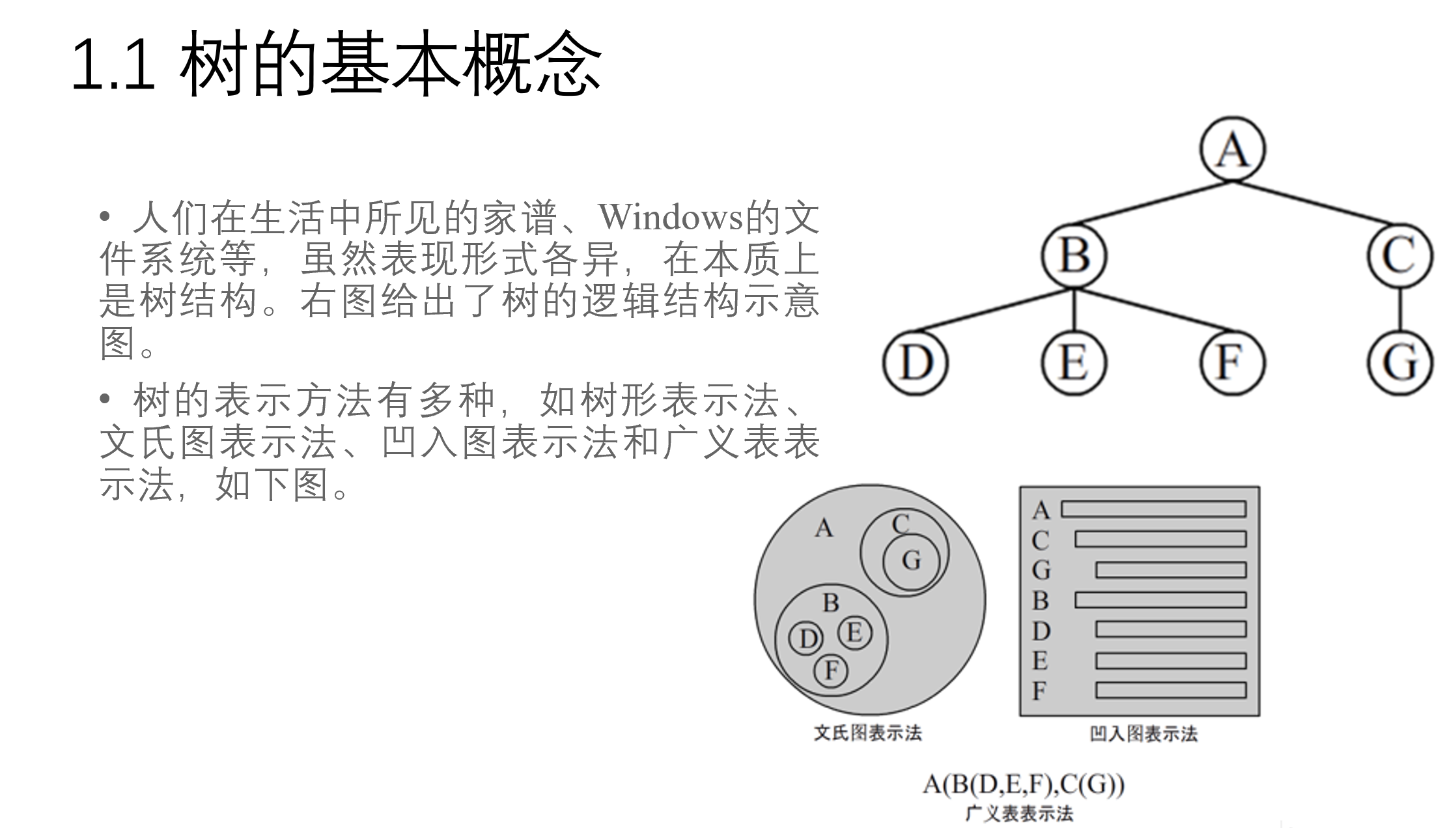
树是数据元素之间具有层次关系的非线性结构,是由n个结点构成的有限集合,结点数为0的树叫空树。树必须满足以下条件。
(1) 有且仅有一个被称为根的结点。
(2) 其余结点可分为m个互不相交的有限集合,每个集合又构成一棵树,叫根结点的子树。
与线性结构不同,树中的数据元素具有一对多的逻辑关系,除根结点以外,每个数据元素可以有多个后继但有且仅有一个前驱,反映了数据元素之间的层次关系。
树是递归定义的。结点是树的基本单位,若干个结点组成一棵子树,若干棵互不相交的子树组成一棵树。
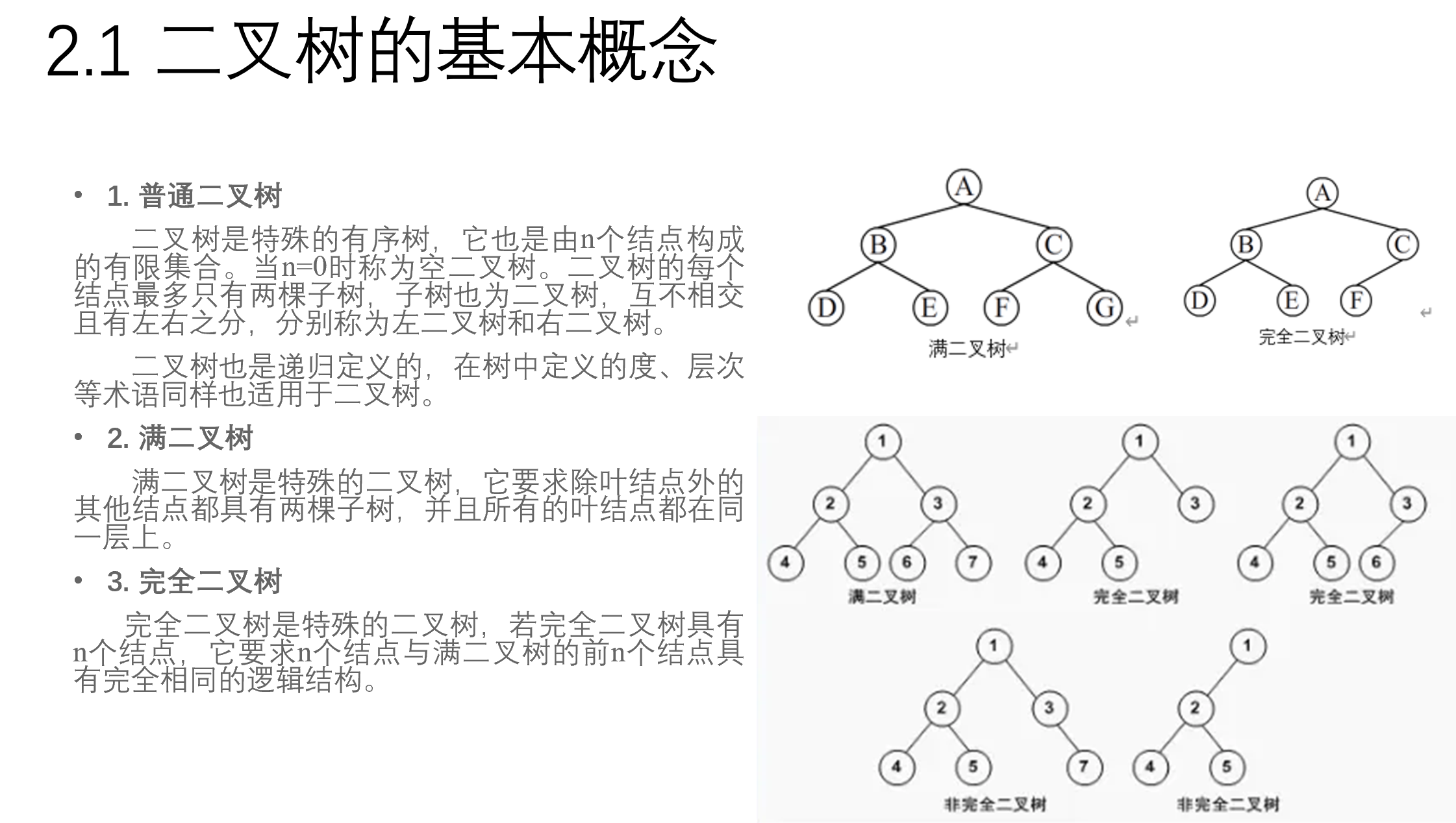
2. 二叉树




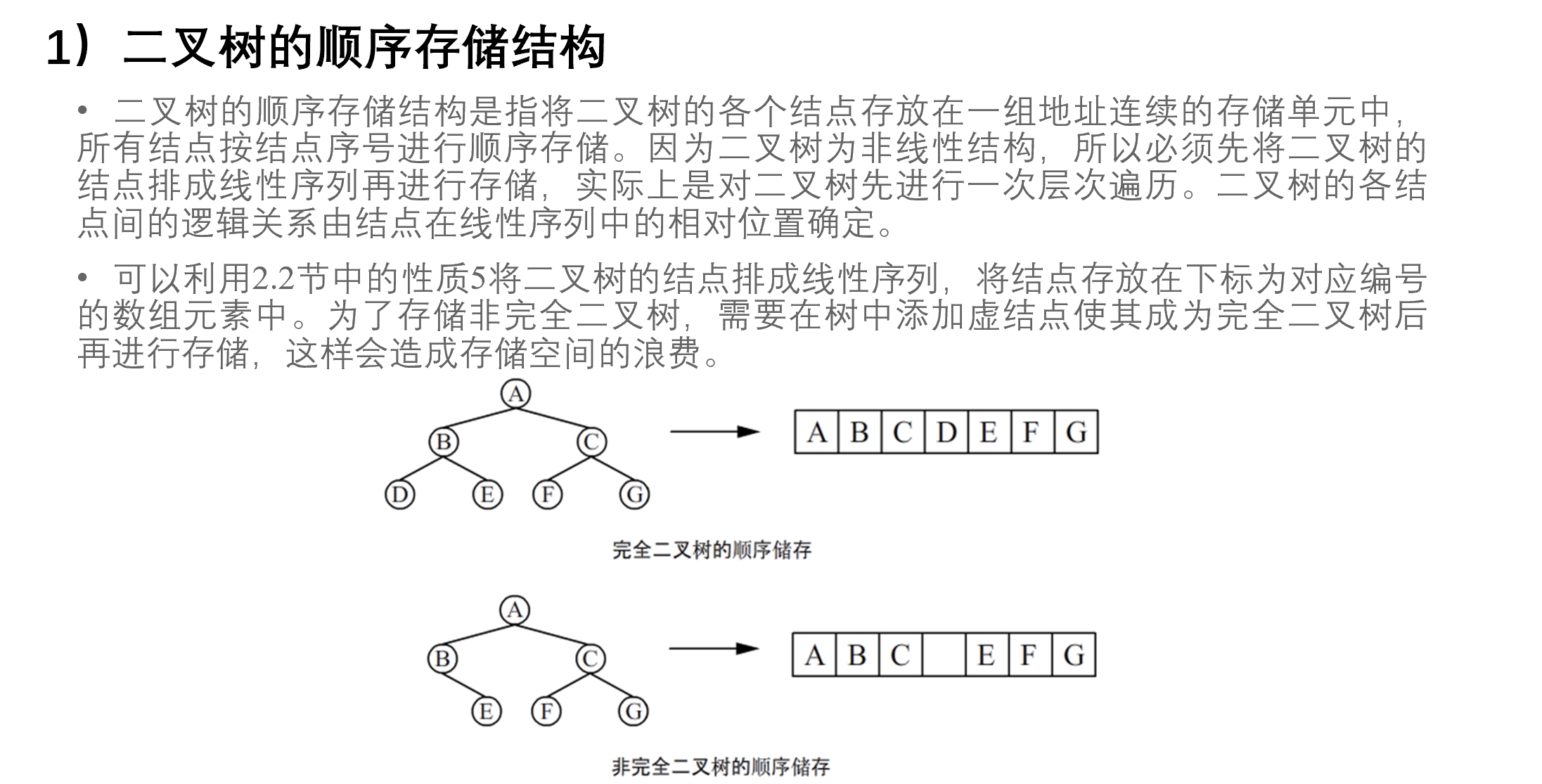
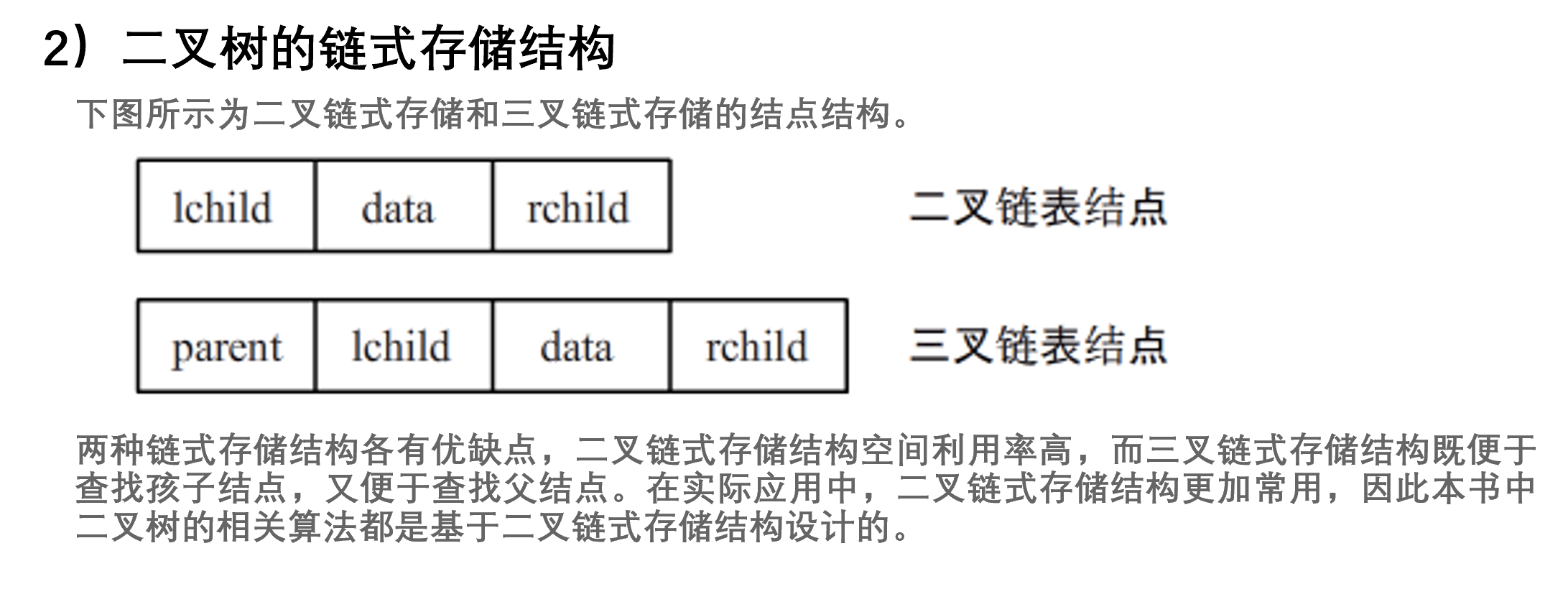
2)二叉树的链式存储结构
二叉树的链式存储结构是指将二叉树的各个结点随机存放在存储空间中,二叉树的各结点间的逻辑关系由指针确定。每个结点至少要有两条链分别连接左、右孩子结点才能表达二叉树的层次关系。根据指针域个数的不同,二叉树的链式存储结构又分为以下两种:
a.二叉链式存储结构
二叉树的每个结点设置两个指针域和一个数据域。数据域中存放结点的值,指针域中存放左、右孩子结点的存储地址。
采用二叉链表存储二叉树,每个结点只存储了到其孩子结点的单向关系,没有存储到其父结点的关系,因此要获得父结点将花费较多的时间,需要从根结点开始在二叉树中进行查找,所花费的时间是遍历部分二叉树的时间,且与查找结点所处的位置有关。
b. 三叉链式存储结构
二叉树的每个结点设置3个指针域和一个数据域。数据域中存放结点的值,指针域中存放左、右孩子结点和父结点的存储地址。


二叉树的遍历是指沿着某条搜索路径访问二叉树的结点,每个结点被访问的次数有且仅有一次。
1)二叉树的遍历方法
二叉树通常可划分为3个部分,即根结点、左子树和右子树。根据3个部分的访问顺序不同,可将二叉树的遍历方法分为以下几种。
a. 层次遍历
自上而下、从左到右依次访问每层的结点。
b. 先序遍历
先访问根结点,再先序遍历左子树,最后先序遍历右子树。
c. 中序遍历
先中序遍历左子树,再访问根结点,最后中序遍历右子树。
d. 后序遍历
先后序遍历左子树,再后序遍历右子树,最后访问根结点。


3)二叉树遍历操作实现的非递归算法
二叉树遍历操作的递归算法结构简洁,易于实现,但是在时间上开销较大,运行效率较低,为了解决这一问题,可以将递归算法转换为非递归算法,转换方式有以下两种:
a.使用临时遍历保存中间结果,用循环结构代替递归过程;
b.利用栈保存中间结果。
二叉树遍历操作实现的非递归算法利用栈结构通过回溯访问二叉树的每个结点。
A. 先序遍历
先序遍历从二叉树的根结点出发,沿着该结点的左子树向下搜索,每遇到一个结点先访问该结点,并将该结点的右子树入栈。先序遍历左子树完成后再从栈顶弹出右子树的根结点,然后采用相同的方法先序遍历右子树,直到二叉树的所有结点都被访问。其主要步骤如下:
(1) 将二叉树的根结点入栈。
(2) 若栈非空,将结点从栈中弹出并访问。
(3) 依次访问当前访问结点的左孩子结点,并将当前结点的右孩子结点入栈。
(4) 重复步骤(2)和(3),直到栈为空。

B. 中序遍历
中序遍历从二叉树的根结点出发,沿着该结点的左子树向下搜索,每遇到一个结点就使其入栈,直到结点的左孩子结点为空。再从栈顶弹出结点并访问,然后采用相同的方法中序遍历结点的右子树,直到二叉树的所有结点都被访问。其主要步骤如下:
(1) 将二叉树的根结点入栈。
(2) 若栈非空,将栈顶结点的左孩子结点依次入栈,直到栈顶结点的左孩子结点为空。
(3) 将栈顶结点弹出并访问,并使栈顶结点的右孩子结点入栈。
(4) 重复步骤(2)和(3),直到栈为空。

C. 后序遍历
后序遍历从二叉树的根结点出发,沿着该结点的左子树向下搜索,每遇到一个结点需要判断其是否为第一次经过,若是则使结点入栈,后序遍历该结点的左子树,完成后再遍历该结点的右子树,最后从栈顶弹出该结点并访问。后序遍历算法的实现需要引入两个变量,一个为访问标记变量flag,用于标记栈顶结点是否被访问,若flag=true,证明该结点已被访问,其左子树和右子树已经遍历完毕,可继续弹出栈顶结点,否则需要先遍历栈顶结点的右子树; 一个为结点指针t,指向最后一个被访问的结点,查看栈顶结点的右孩子结点,证明此结点的右子树已经遍历完毕,栈顶结点可出栈并访问。其主要步骤如下:
(1) 将二叉树的根结点入栈,t赋值为空。
(2) 若栈非空,将栈顶结点的左孩子结点依次入栈,直到栈顶结点的左孩子结点为空。
(3) 若栈非空,查看栈顶结点的右孩子结点,若右孩子结点为空或者与p相等,则弹出栈顶结点并访问,同时使t指向该结点,并置flag为true; 否则将栈顶结点的右孩子结点入栈,并置flag为false。
(4) 若flag为true,重复步骤(3); 否则重复步骤(2)和(3),直到栈为空。

1)二叉树上的查找算法
二叉树上的查找是在二叉树中查找值为x的结点,若找到返回该结点,否则返回空值,可以在二叉树的先序遍历过程中进行查找,主要步骤如下:
(1) 若二叉树为空,则不存在值为x的结点,返回空值; 否则将根结点的值与x进行比较,若相等,返回该结点。
(2) 若根结点的值与x的值不等,则在左子树中进行查找,若找到,则返回该结点。
(3) 若没有找到,则在根结点的右子树中进行查找,若找到,返回该结点,否则返回空值。

2)统计二叉树的结点个数的算法
二叉树的结点个数等于根结点加上左、右子树的结点的个数,可以利用二叉树的先序遍历序列,引入一个计数变量count,count的初值为0,每访问根结点一次就将count的值加1,其主要操作步骤如下:
(1) count值初始化为0。
(2) 若二叉树为空,返回count值。
(3) 若二叉树非空,则count值加1,
统计根结点的左子树的结点个数,
并将其加到count中;
统计根结点的右子树的结点个数,
并将其加到count中。

3)求二叉树的深度
二叉树的深度是所有结点的层次数的最大值加1,也就是左子树和右子树的深度的最大值加1,可以采用后序遍历的递归算法解决此问题,其主要步骤如下:
(1) 若二叉树为空,返回0。
(2) 若二叉树非空,
求左子树的深度、求右子树的深度。
(3) 比较左、右子树的深度,
取最大值加1即为二叉树的深度。
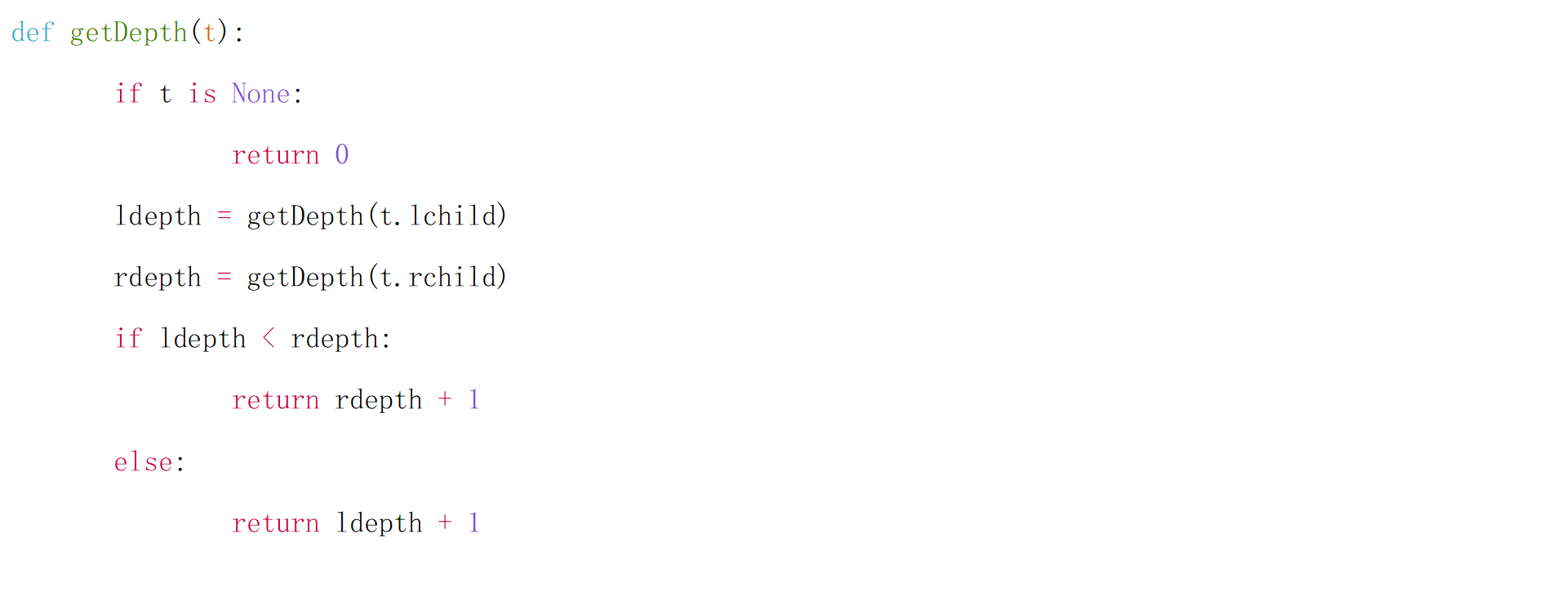
二叉树遍历操作可使非线性结构的树转换成线性序列。先序遍历序列和后序遍历序列反映父结点和孩子结点间的层次关系,中序遍历序列反映兄弟结点间的左右次序关系。因为二叉树是具有层次关系的结点构成的非线性结构,并且每个结点的孩子结点具有左右次序,所以已知一种遍历序列无法唯一确定一棵二叉树,只有同时知道中序和先序遍历序列,或者同时知道中序和后序遍历序列,才能同时确定结点的层次关系和结点的左右次序,才能唯一确定一棵二叉树。

1)由中序和先序遍历序列建立二叉树
其主要步骤为如下:
(1) 取先序遍历序列的第一个结点作为根结点,序列的结点个数为n。
(2) 在中序遍历序列中寻找根结点,其位置为i,可确定在中序遍历序列中根结点之前的i个结点构成的序列为根结点的左子树中序遍历序列,根结点之后的n-i-1个结点构成的序列为根结点的右子树中序遍历序列。
(3) 在先序遍历序列中根结点之后的i个结点构成的序列为根结点的左子树先序遍历序列,先序遍历序列之后的n-i-1个结点构成的序列为根结点的右子树先序遍历序列。
(4) 对左、右子树重复步骤(1)、(2)、(3),确定左、右子树的根结点和子树的左右、子树。
(5) 算法递归进行即可建立一棵二叉树。
1)由中序和先序遍历序列
建立二叉树
假设二叉树的先序遍历序列为ABECFG、
中序遍历序列为BEAFCG,
由中序和先序遍历序列建立二叉树的过程
如图所示:
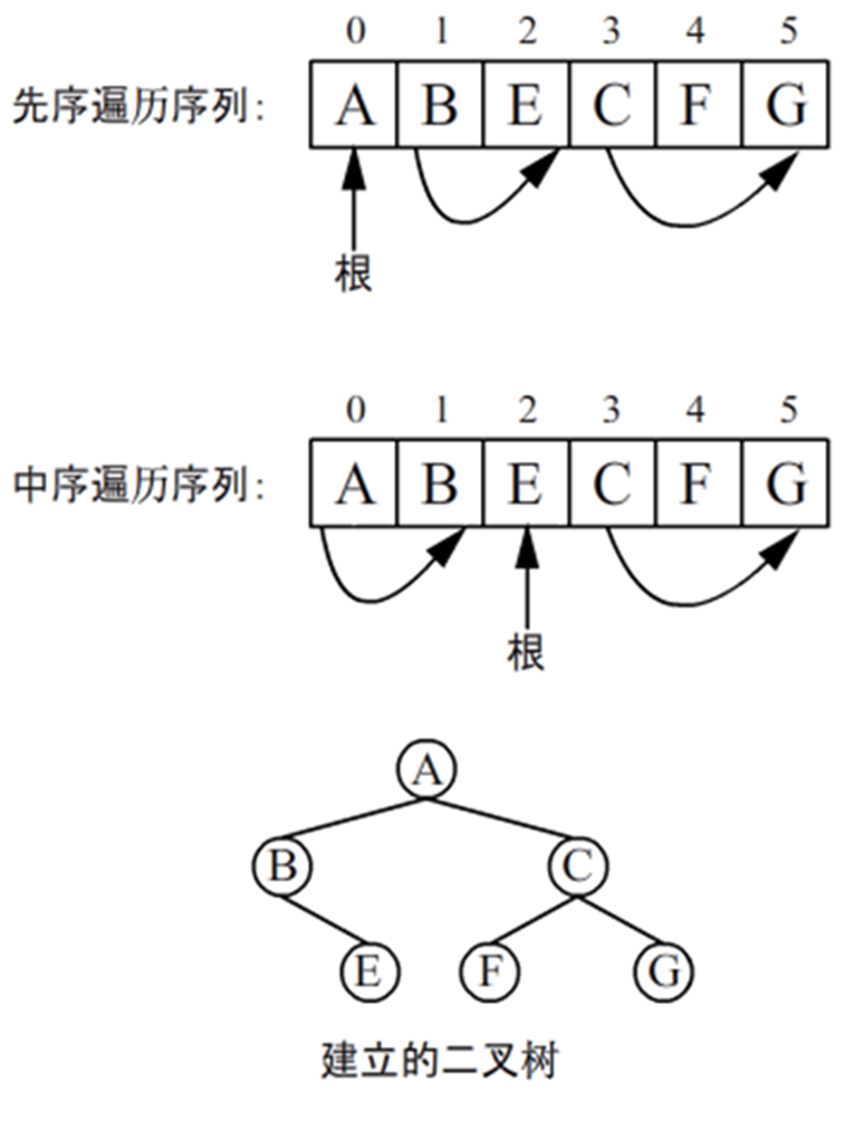
1)由中序和先序遍历序列建立二叉树
算法如下:

2)由标明空子树的先序遍历序列创建二叉树
其主要步骤如下:
(1) 从先序遍历序列中依次读取字符。
(2) 若字符为#,建立空子树。
(3) 建立左子树。
(4) 建立右子树。
2)由标明空子树的先序遍历序列创建二叉树
算法如下:

【例5.3】已知二叉树的中序和后序序列分别为CBEDAFIGH和CEDBIFHGA,试构造该二叉树。
解: 二叉树的构造过程如下图所示。图©即为构造出的二叉树。

3. 哈夫曼树及哈夫曼编码
目前常用的图像、音频、视频等多媒体信息由于数据量大,必须对它们采用数据压缩技术来存储和传输。数据压缩技术通过对数据进行重新编码来压缩存储,以便减少数据占用的存储空间,在使用时再进行解压缩,恢复数据的原有特性。
其压缩方法主要有有损压缩和无损压缩两种。有损压缩是指压缩过程中可能会丢失数据信息,如将BMP位图压缩成JPEG格式的图像,会有精度损失; 无损压缩是指压缩存储数据的全部信息,确保解压后的数据不丢失。哈夫曼编码是数据压缩技术中的无损压缩技术。
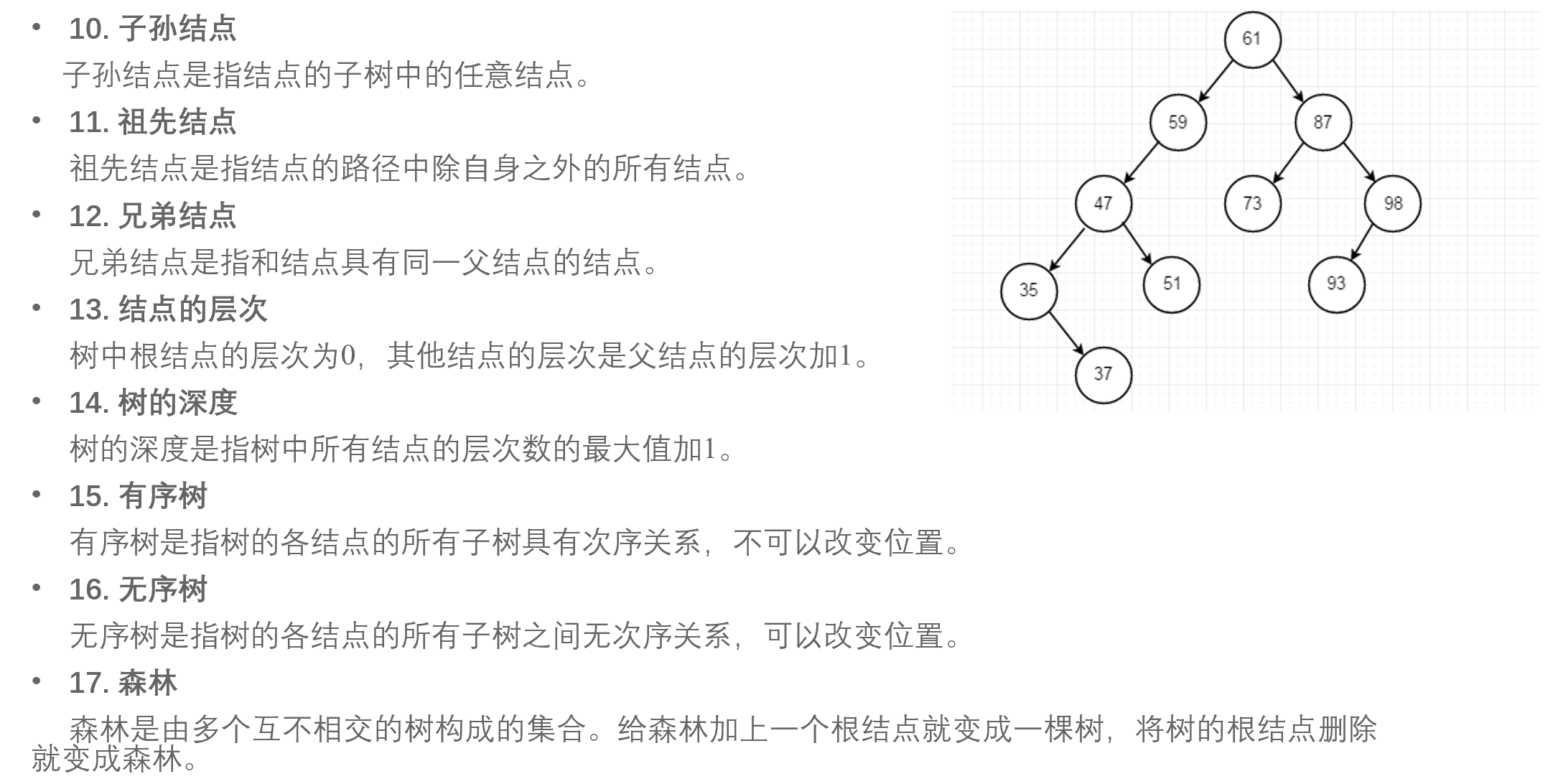
- 结点间的路径
结点间的路径是指从一个结点到另一个结点所经过的结点序列。从根结点到X结点有且仅 有一条路径。 - 结点的路径长度
结点的路径长度是指从根结点到结点的路径上的边数。 - 结点的权
结点的权是指人给结点赋予的一个具有某种实际意义的数值。 - 结点的带权路径长度
结点的带权路径长度是指结点的权值和结点的路径长度的乘积。 - 树的带权路径长度
树的带权路径长度是指树的叶结点的带权路径长度之和。 - 最优二叉树
最优二叉树是指给定n个带有权值的结点作为叶结点构造出的具有最小带权路径长度的 二叉树。最优二叉树也叫哈夫曼树。
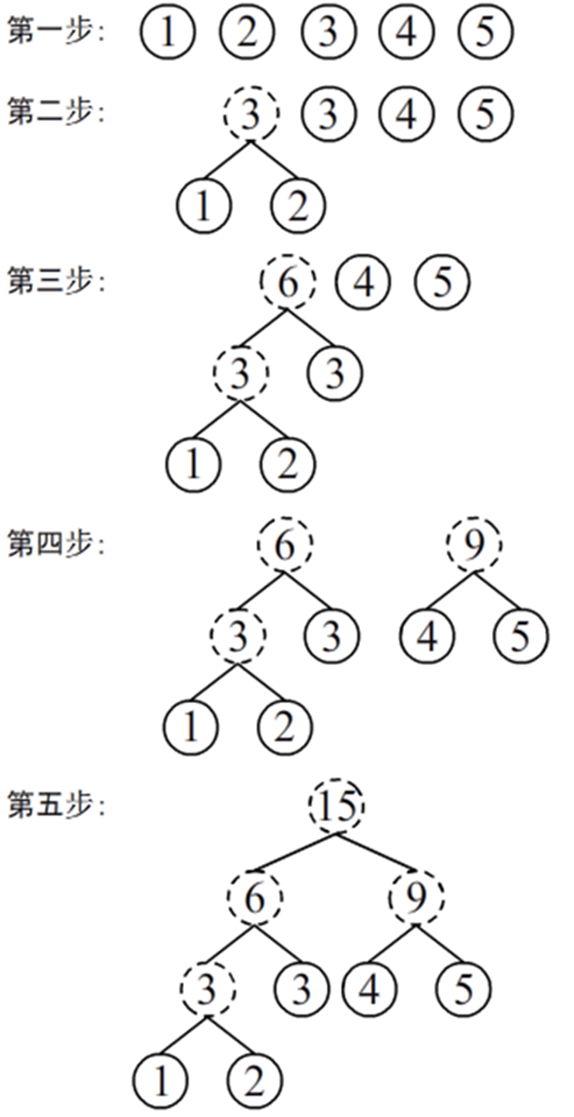
给定n个叶结点,它们的权值分别是{w1,w2,…,wn},构造相应的哈夫曼树的主要步骤如下:
(1) 构造由n棵二叉树组成的森林,每棵二叉树只有一个根结点,根结点的权值分别为{w1,w2,…,wn}。
(2) 在森林中选取根结点权值最小和次小的两棵二叉树分别作为左子树和右子树去构造一棵新的二叉树,新二叉树的根结点权值为两棵子树的根结点权值之和。
(3) 将两棵二叉树从森林中删除,并将新的二叉树添加到森林中。
(4) 重复步骤(2)和(3),直到森林中只有一棵二叉树,此二叉树即为哈夫曼树。
假设给定的权值为{1,2,3,4,5},右图展示了哈夫曼树的构造过程。

在传送信息时需要将信息符号转化成二进制组成的符号串,一般每个字符由一个字节或两个字节表示,即8或16个位数。为了提高存储和传输效率,需要设计对字符集进行二进制编码的规则,使得利用这种规则对信息进行编码时编码位数最小,即需要传输的信息量最小。
哈夫曼编码是一种变长的编码方案,数据的编码因其使用频率的不同而长短不一,使用频率高的数据其编码较短,使用频率低的数据其编码较长,从而使所有数据的编码总长度最短。各数据的使用频率通过在全部数据中统计重复数据的出现次数获得。
又因为在编码序列中若使用前缀相同的编码来表示不同的字符会造成二义性,额外的分隔符号会造成传输信息量的增加,为了省去不必要的分隔符号,要求每一个字符的编码都不是另一个字符的前缀,即每个字符的编码都是前缀编码。
利用哈夫曼树构造出的哈夫曼编码是一种最优前缀编码,构造的主要步骤如下:
对于具有n个字符的字符集,将字符的频度作为叶结点的权值,产生n个带权叶结点。
根据上面章节中介绍的构造哈夫曼树的方法利用n个叶结点构造哈夫曼树。
根据哈夫曼编码规则将哈夫曼树中的每一条左分支标记为0、每一条右分支标记为1,则可得到每个叶结点的哈夫曼编码。
哈夫曼编码的译码过程是构造过程的逆过程,从哈夫曼树的根结点开始对编码的每一位进行判别,如果为0进入左子树,如果为1进入右子树,直到到达叶结点,即译出了一个字符。
构造哈夫曼树需要从子结点到父结点的操作,译码时需要从父结点到子结点的操作,所以为了提高算法的效率将哈夫曼树的结点设计为三叉链式存储结构。一个数据域存储结点的权值,一个标记域flag标记结点是否已经加入到哈夫曼树中,3个指针域分别存储着指向父结点、孩子结点的地址。
结点类的描述如下:

构造哈夫曼树算法,如下:


【算法】若字符与出现频率对应关系如:[(‘a’,5),(‘b’,2),(‘c’,9),(‘d’,11),(‘e’,8),(‘f’,3),(‘g’,7)]求哈夫曼编码

输出如下:

4. 树和森林
一棵树包含各结点间的层次关系和兄弟关系,两种关系的存储结构不同。
树的层次关系必须采用链式存储结构存储,通过链连接父结点和孩子结点。
一个结点的多个孩子结点(互称兄弟结点)之间是线性关系,可以采用顺序存储结构或者链式存储结构。
a. 树的父母孩子链表
树的父母孩子链表采用顺序存储结构存储多个孩子结点,其中children数组 存储多个孩子结点,各结点的children数组元素长度不同,为孩子个数。
b. 树的父母孩子兄弟链表
树的父母孩子兄弟链表采用链式存储结构存储多个孩子结点,结点其中 child链指向一个孩子结点,sibling链指向下一个兄弟结点。
森林也可以使用父母孩子兄弟链表进行存储,这种存储结构实际上是把一棵树转换成一棵二叉树存储。其存储规则如下:
(1) 每个结点采用child链指向其中一个孩子结点,多个孩子结点之间由sibling链连接起来,组成一条具有兄弟结点关系的单链表。
(2) 将每棵树采用树的父母孩子兄弟链表存储。
(3) 森林中的多棵树之间是兄弟关系,将这些树通过根的sibling链连接起来。
树的孩子优先遍历规则主要有两种,即先序遍历和后序遍历。树的遍历规则也是递归的。
(1) 树的先序遍历: 访问根结点; 按从左到右的次序遍历根的每一棵子树。
(2) 树的后序遍历: 按从左到右的次序遍历根的每一棵子树; 访问根结点。
树的层次遍历规则同二叉树。
小结
(1) 树是数据元素之间具有层次关系的非线性结构,是由n个结点构成的有限集合。与线性结构不同,树中的数据元素具有一对多的逻辑关系。
(2) 二叉树是特殊的有序树,它也是由n个结点构成的有限集合。当n=0时称为空二叉树。二叉树的每个结点最多只有两棵子树,子树也为二叉树,互不相交且有左、右之分,分别称为左二叉树和右二叉树。
(3) 二叉树的存储结构分为两种,即顺序存储结构和链式存储结构。二叉树的顺序存储结构是指将二叉树的各个结点存放在一组地址连续的存储单元中,所有结点按结点序号进行顺序存储; 二叉树的链式存储结构是指将二叉树的各个结点随机存放在存储空间中,二叉树的各结点间的逻辑关系由指针确定。
(4) 二叉树具有先序遍历、中序遍历、后序遍历和层次遍历4种遍历方式。
(5) 最优二叉树是指给定n个带有权值的结点作为叶结点构造出的具有最小带权路径长度的二叉树,也叫哈夫曼树。
(6) 哈夫曼编码是数据压缩技术中的无损压缩技术,是一种变长的编码方案,使所有数据的编码总长度最短。