痛点剖析

随着企业生产环境的日益复杂化，不同生产设备间的协调性问题尤为凸显。

1、不同设备往往基于各自的技术标准、通信协议和操作系统设计，这使得它们之间的数据交换和指令传递存在显著的障碍。

2、技术上的不兼容性导致设备间难以实现无缝对接和协同工作，从而直接影响了企业的生产效率。

3、云端集成控制系统，存在响应速度慢，断网断电失控，稳定性不足，安全性不足的缺点。

为实现跨设备自动化协同，解决设备间的兼容性问题，中服云基于物联网开发平台，成功研发“边缘端自动化流程编排工具”。旨在推动设备间的标准化和统一化，提升设备的互操作性和生产协同。

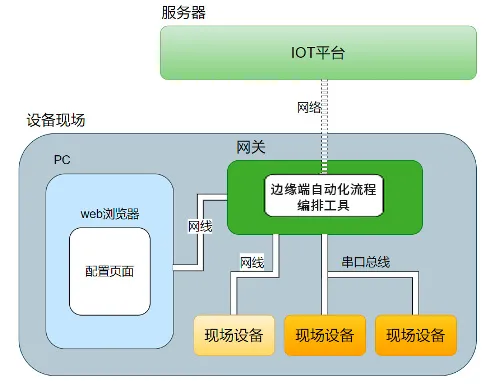
 （边缘自动化流程编排工具）

功能介绍：

边缘端自动化流程编排工具为用户提供一个自定义业务流程编排、执行工具(例如:根据客户现场需求编排一个蓄水池定时自动检测水位、调节阀、开关水泵蓄水场景)，由触发条件、业务流、输出三部分组成。

1、触发条件为当前业务流图开始节点，包括数据触发和定时触发；

2、业务流为当前业务流图业务流程处理逻辑，包括条件分流、选择器分流、合流、定时器。

业务流界面主要操作包括：添加业务流图、修改名称、导入与导出流图、删除流图、流图启停、保存、业务流监视、日志查看。

3、输出为业务流执行单元,将指定数据写入执行设备。

核心优势：

1、边缘端自动化流程编排工具支持网关在脱离平台的情况下，独立指挥现场设备按编排的逻辑正常运行。

2、通过配置插件，可支持不同设备的快速低成本接入。

3、企业的上手难度比较低，配置的便捷性较高、可适应不同的生产环境。

边缘端自动化流程编排工具在设备网关中实现流程的自动化编排和管理，通过这一工具，企业可以更加灵活地调整和优化生产流程，实现生产资源的合理配置和高效利用。同时，它还能实时监控生产过程中的数据，帮助企业及时发现和解决问题，从而提升生产效率和产品质量。