【五十六】【算法分析与设计】线段树之add+query操作，pair表示节点，自定义类型表示节点，真树结构实现线段树与数组实现线段树

news/2024/12/22 19:51:47/

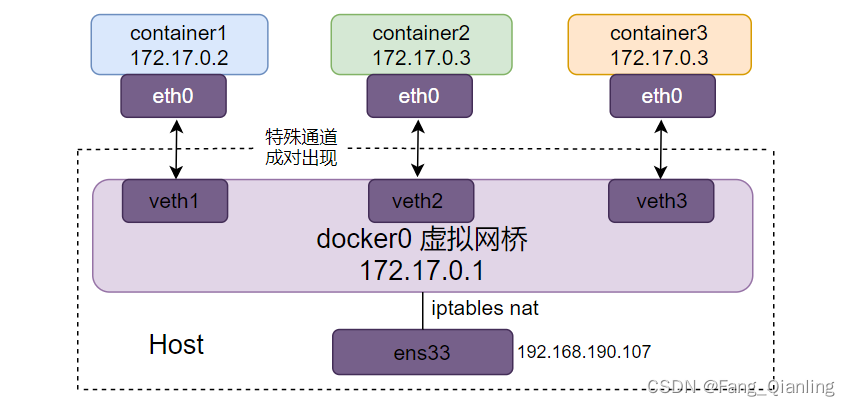
线段树解决的问题

给你一个nums数组，1.L~R区间上的值全部加C。2.L~R区间上的值全部变成C。3.对L~R区间上求和操作。

对于第一个方法，如果正常遍历L~R加C，时间复杂度是O(N)。

对于第二个方法，如果正常遍历L~R=C，时间复杂度是O(N)。

对于第三个方法，如果正常遍历L~R得到sum累加和，时间复杂度是O(N)。

线段树可以做到O(logN）时间复杂度做到这三个方法。

线段树

nums数组对应的线段树构造

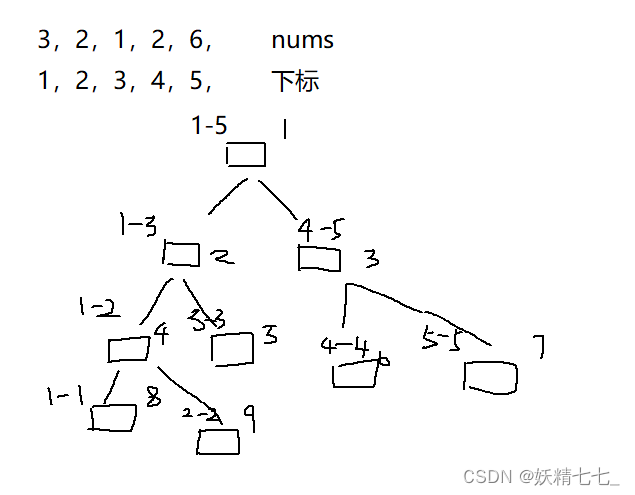
我有一个nums数组，3，2，1，2，6，下标依次从1开始，分别是1，2，3，4，5

我构建一个sum数组，sum数组下标为1的位置，表示nums数组1~5的累加和。

对于sum数组任意一个位置i，左孩子的下标一定是2*i,右孩子的下标一定是2*i+1，父亲的下标一定是i/2。

对于sum数组任意一个位置i，包含的信息是nums数组中l~r区间上的和，在sum数组的下标是i。

左孩子包含的信息是nusm数组中l~mid区间上的和，在sum数组的下标是i*2。其中mid=(l+r)>>1=（l+r）/2。

左孩子包含的信息是nusm数组中mid+1~r区间上的和，在sum数组的下标是i*2+1。其中mid=(l+r)>>1=（l+r）/2。

lazy懒数组

1.

lazy懒数组是一个和sum数组大小一样，并且树结构、下标一一对应的数组。也可以看作是sum数组的另一个信息的存储。

如果sum数组中不存放int类型，而是存储结构体类型或者pair类型，使得每一个节点都可以存放两个信息，lazy懒数组就可以省去，因为它表示的信息以及存在了每一个节点中，不需要再来一个数组与之绑定。

2.

lazy懒数组存储的是任务，例如我想要add(L,R,C,)操作，将nums数组中L~R区间上的值都统一加C。

此时我更新的不是nums数组，而是sum数组。

我需要把sum数组中所有位置的数据都维护好。

例如我希望将nums数组中4~5位置上的值都统一加2。

那么我需要维护的位置是1、3、6、7，四个位置。

6、7位置的sum值实际上不需要维护，因为到3位置的时候，3位置表示的是4~5的区间和，这个区间在任务区间内，因此维护3位置的sum值，lazy[3]=2。此时存储任务，懒得下发任务。

因此需要维护得位置只有1和3。

3.

什么时候可以懒住任务，什么时候不能懒住任务？

当我当前得节点信息表示得区间是 l~r，这个区间被任务区间包含在内，即L<=l&&r<=R的时候就可以懒住任务不再下发。反正则不能懒住任务。

pushup函数

 

        void pushup(int rt) {sum[rt] = sum[rt << 1] + sum[rt << 1 | 1];}
 

如果我左右孩子sum值维护好了，调用pushup函数维护当前节点rt的sum值。
 

pushudown函数
 

 

        void pushdown(int rt, int ln, int rn) {if (lazy[rt] != 0) {lazy[rt << 1] += lazy[rt];lazy[rt << 1 | 1] += lazy[rt];sum[rt << 1] += lazy[rt] * ln;sum[rt << 1 | 1] += lazy[rt] * rn;lazy[rt] = 0;}}
 

将当前节点的任务下发一层，维护好执行完任务后的sum值，注意此时只是下发一层，也就是让下一层执行任务并且懒住。因为当前节点懒住的任务，说明当前节点的区间 l~r一定全部被L~R包含，那么当前节点的左右孩子也一定全部被L~R包含。所以让孩子执行任务后懒住任务。
 

add(L,R,C)对nums数组区间统一加C操作
 

 

 

 

        void _add(int L, int R, int C, int l, int r, int rt) {//维护rt节点的sum值，如果可以懒就懒，不可以懒就不懒,不懒的时候需要发任务维护下一层sumif (r < L || R < l) return;if (L <= l && r <= R) {sum[rt] += C * (r - l + 1);lazy[rt] += C;return;}int mid = (l + r) >> 1;pushdown(rt, mid - l + 1, r - (mid + 1) + 1);_add(L, R, C, l, mid, rt << 1);_add(L, R, C, mid + 1, r, rt << 1 | 1);pushup(rt);}
 

_add(L,R,C,l,r,rt)递归函数，表示将nums数组中L~R区间全部加上C，nums对应的sum树当前节点的信息是 l~r区间和，在sum数组中下标是rt。
 

递归函数定义是，维护当前rt位置的sum值，如果任务能懒则懒，懒不住就递归到下一层节点，重复操作，能懒则懒。
 

如果当前节点区间范围不在L~R范围内，也就是没有一个重合区间，直接返回。
 

如果当前节点区间范围在L~R范围内，并且是所有元素都在这个L~R区间内，说明可以懒住任务。此时直接维护当前节点的sum值，然后维护当前节点的lazy值，返回即可，任务懒住不再下发。
 

如果上面两种情况没中，说明此时 l~r区间有一部分在L~R范围内，有一部分不在L~R范围内。此时先把当前节点存放的任务下发一层，意思是当前节点存放的任务，让下一层维护好sum值。然后将当前任务下发到下一层，维护好sum值。
 

让孩子执行完懒住的任务并且维护好sum后，还需要让孩子执行新的任务维护sum值，能不能懒住再看具体情况。
 

执行完这两个任务之后，左右孩子的sum值一定维护好了，pushup维护当前节点的sum值。
 

当左右孩子sum值维护好，用他们的值维护自己即可。
 

query(L,R)查询nums数组区间和操作
 

 

 

 

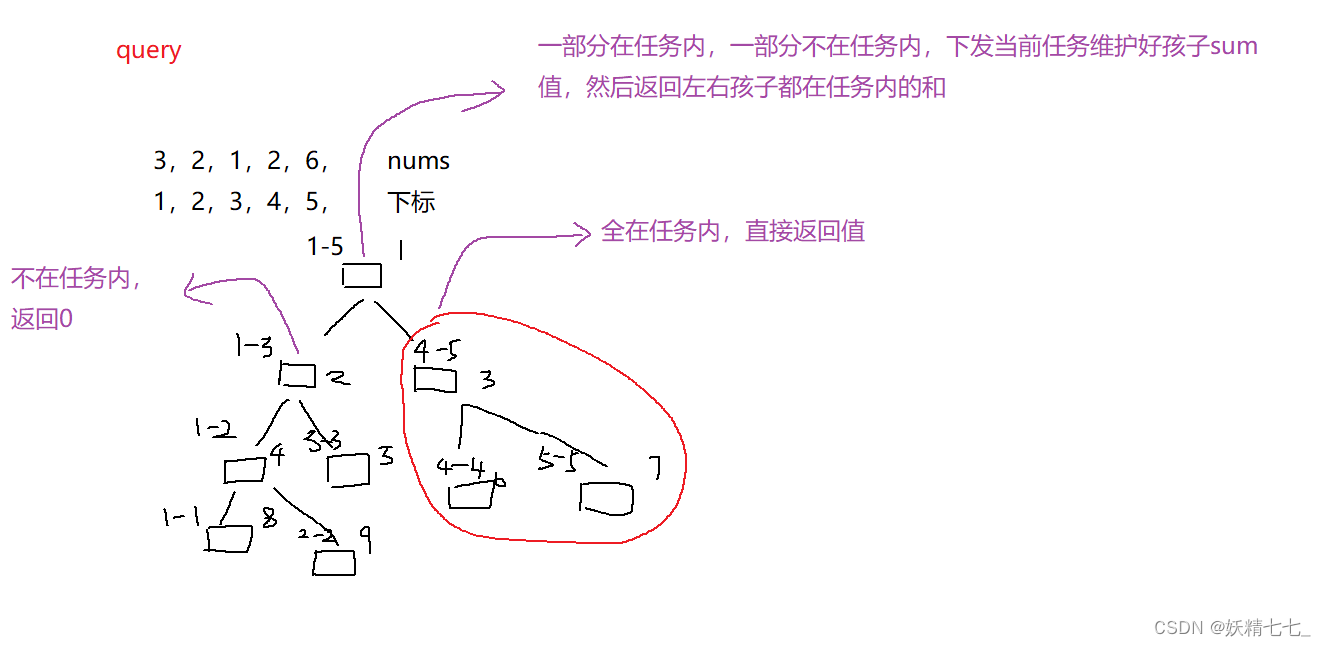
        int _query(int L, int R, int l, int r, int rt) {//返回区间和，包裹住了就整个返回，不能就分开加和返回,分开加和需要把任务下发维护下一层sumif (r < L || R < l) {return 0;}if (L <= l && r <= R) {return sum[rt];}int mid = (l + r) >> 1;pushdown(rt, mid - l + 1, r - (mid + 1) + 1);return _query(L, R, l, mid, rt << 1) + _query(L, R, mid + 1, r, rt << 1 | 1);}
 

我需要查询L~R区间的累加和，递归函数_query表示任务是查询L~R区间和，当前节点信息是nums数组l~r区间和，再sum数组中下标是rt。
 

如果当前节点区间范围不在L~R范围内，也就是没有一个重合区间，直接返回 0。
 

如果当前节点区间范围在L~R范围内，并且是所有元素都在这个L~R区间内，说明此时节点的sum值是我们需要的，直接返回sum[rt]。
 

如果当前节点区间范围有一部分在L~R范围内，一部分不在L~R范围内，将当前任务下发一层，让孩子节点做任务，然后懒住任务，这一步表示维护好下一层的sum值，维护好之后，当前层的sum值等于左右孩子sum值的和。
 

sum数组，lazy数组需要开多大的空间？
 

将nums数组离散化成树状数组，nums大小是size，sum和lazy开辟4*size空间即可。
 

小总结
 

 

 

1.
 

add操作和query操作，每一次访问某一个节点的时候，该节点的sum值一定是维护好的。
 

2.
 

add操作，我当前节点的范围 l~r在L~R内部，全部都在内部，说明当前树的值整个需要维护，但是我只维护根节点的值，任务懒住不下发给子树。
 

add操作，如果当前节点的范围 l~r一部分在L~R内，一部分不在，我只需要更新在内部的sum值，我一定能在子树中找到一棵树，表示的区间 l~r全部位于L~R内，并且所有这样的树的范围合并起来，一定是完整的L~R。
 

我只需要维护每一棵这样的树的根sum值，然后懒住任务不下发。
 

3.
 

query操作，我当前节点的范围 l~r在L~R内部，全部都在内部，说明当前树的值整个是我需要用到的值，并且当前sum值是维护好的，我直接返回即可。
 

query操作，如果当前节点的范围 l~r一部分在L~R内，一部分不在，我一定能在子树中找到一棵树，表示的区间 l~r全部位于L~R内，并且所有这样的树的范围合并起来，一定是完整的L~R。
 

所有树的sum值得累加我就我们需要得结果。
 

线段树代码
 

查询区间和+区间add （模板）
 

 

class SegmentTree {//查询区间和+区间add （模板）
private:vector<int> sum;vector<int> lazy;int size;void pushup(int rt) {sum[rt] = sum[rt << 1] + sum[rt << 1 | 1];}void pushdown(int rt, int ln, int rn) {if (lazy[rt] != 0) {lazy[rt << 1] += lazy[rt];lazy[rt << 1 | 1] += lazy[rt];sum[rt << 1] += lazy[rt] * ln;sum[rt << 1 | 1] += lazy[rt] * rn;lazy[rt] = 0;}}void _add(int L, int R, int C, int l, int r, int rt) {//维护rt节点的sum值，如果可以懒就懒，不可以懒就不懒,不懒的时候需要发任务维护下一层sumif (r < L || R < l) return;if (L <= l && r <= R) {sum[rt] += C * (r - l + 1);lazy[rt] += C;return;}int mid = (l + r) >> 1;pushdown(rt, mid - l + 1, r - (mid + 1) + 1);_add(L, R, C, l, mid, rt << 1);_add(L, R, C, mid + 1, r, rt << 1 | 1);pushup(rt);}int _query(int L, int R, int l, int r, int rt) {//返回区间和，包裹住了就整个返回，不能就分开加和返回,分开加和需要把任务下发维护下一层sumif (r < L || R < l) {return 0;}if (L <= l && r <= R) {return sum[rt];}int mid = (l + r) >> 1;pushdown(rt, mid - l + 1, r - (mid + 1) + 1);return _query(L, R, l, mid, rt << 1) + _query(L, R, mid + 1, r, rt << 1 | 1);}public:SegmentTree(int _size) {size = _size;sum.resize(size << 2);lazy.resize(size << 2);}void add(int L, int R, int C) {_add(L, R, C, 0, size, 1);//区间一一对应，0~size-1 }int query(int L, int R) {return _query(L, R, 0, size, 1);//区间一一对应，0~size-1 }
};int main() {vector<int> nums = { 1,2,3,4,5,6,7,8,9,10 };SegmentTree st(nums.size());for (int i = 0; i < nums.size(); i++)st.add(i, i, nums[i]);cout << st.query(0, nums.size() - 1) << endl;cout << accumulate(nums.begin(), nums.end(), 0) << endl;
}
 

查询区间和+区间add（pair代替lazy数组）
 

 


class SegmentTree {
private:int size;vector<pair<int, int>> node;//first---sum,second---lazyvoid pushup(int rt) {node[rt].first = node[rt << 1].first + node[rt << 1 | 1].first;}void pushdown(int rt, int ln, int rn) {if (node[rt].second != 0) {int c = node[rt].second;node[rt].second = 0;node[rt << 1].first += c;node[rt << 1 | 1].first += c;node[rt << 1].second += c;node[rt << 1 | 1].second += c;}}void _add(int L, int R, int C, int l, int r, int rt) {if (r < L || R < l) {return;}if (L <= l && r <= R) {node[rt].first += C;node[rt].second += C;return;}int mid = (l + r) >> 1;pushdown(rt, mid - l + 1, r - (mid + 1) + 1);_add(L, R, C, l, mid, rt << 1);_add(L, R, C, mid + 1, r, rt << 1 | 1);pushup(rt);}int _query(int L, int R, int l, int r, int rt) {if (r < L || R < l) {return 0;}if (L <= l && r <= R) {return node[rt].first;}int mid = (l + r) >> 1;pushdown(rt, mid - l + 1, r - (mid + 1) + 1);return _query(L, R, l, mid, rt << 1) + _query(L, R, mid + 1, r, rt << 1 | 1);}public:SegmentTree(int n) {size = n;node.resize(size << 2);}void add(int L, int R, int C) {_add(L, R, C, 0, size - 1, 1);}int query(int L, int R) {return _query(L, R, 0, size - 1, 1);}
};int main() {vector<int> nums = { 1,2,3,4,5,6,7,8,9,10 };SegmentTree st(nums.size());for (int i = 0; i < nums.size(); i++) {st.add(i, i, nums[i]);}cout << st.query(0, nums.size() - 1) << endl;cout << accumulate(nums.begin(), nums.end(), 0) << endl;cout << st.query(0, 5) << endl;cout << accumulate(nums.begin(), nums.begin() + 5 + 1, 0) << endl;
}
 

查询区间和+区间add（自定义类型表示node)
 

 


class SegmentTree {
private:struct Node {int sum;int lazy;};vector<Node> node;int size;void pushup(int rt) {node[rt].sum = node[rt << 1].sum + node[rt << 1 | 1].sum;}void pushdown(int rt, int ln, int rn) {if (node[rt].lazy != 0) {int c = node[rt].lazy;node[rt].lazy = 0;node[rt << 1].sum += c;node[rt << 1].lazy += c;node[rt << 1 | 1].sum += c;node[rt << 1 | 1].lazy += c;}}void _add(int L, int R, int C, int l, int r, int rt) {if (r < L || R < l) {return;}if (L <= l && r <= R) {node[rt].sum += C;node[rt].lazy += C;return;}int mid = (l + r) >> 1;pushdown(rt, mid - l + 1, r - (mid + 1) + 1);_add(L, R, C, l, mid, rt << 1);_add(L, R, C, mid + 1, r, rt << 1 | 1);pushup(rt);}int _query(int L, int R, int l, int r, int rt) {if (r < L || R < l) {return 0;}if (L <= l && r <= R) {return node[rt].sum;}int mid = (l + r) >> 1;pushdown(rt, mid - l + 1, r - (mid + 1) + 1);return  _query(L, R, l, mid, rt << 1) +_query(L, R, mid + 1, r, rt << 1 | 1);}public:SegmentTree(int n) {size = n;node.resize(size << 2);}void add(int L, int R, int C) {_add(L, R, C, 0, size - 1, 1);}int query(int L, int R) {return _query(L, R, 0, size - 1, 1);}
};int main() {vector<int> nums = { 1,2,3,4,5,6,7,8,9,10 };SegmentTree st(nums.size());for (int i = 0; i < nums.size(); i++) {st.add(i, i, nums[i]);}cout << st.query(0, nums.size() - 1) << endl;cout << accumulate(nums.begin(), nums.end(), 0) << endl;cout << st.query(0, 5) << endl;cout << accumulate(nums.begin(), nums.begin() + 5 + 1, 0) << endl;
}

 

查询区间和+区间add（真树结构）
 

 


class SegmentTreeNode {
public:int start, end, sum, lazy;SegmentTreeNode* left;SegmentTreeNode* right;SegmentTreeNode(int start, int end) : start(start), end(end), sum(0), lazy(0), left(nullptr), right(nullptr) {}
};class SegmentTree {
private:SegmentTreeNode* root;SegmentTreeNode* buildTree(vector<int> nums, int start, int end) {if (start > end) {return nullptr;}SegmentTreeNode* node = new SegmentTreeNode(start, end);if (start == end) {node->sum = nums[start];} else {int mid = start + (end - start) / 2;node->left = buildTree(nums, start, mid);node->right = buildTree(nums, mid + 1, end);node->sum = node->left->sum + node->right->sum;}return node;}void addHelper(SegmentTreeNode* node, int L, int R, int C) {if (!node || node->end < L || node->start > R) {return;}if (node->start >= L && node->end <= R) {node->sum += C;node->lazy += C;return;}int mid = node->start + (node->end - node->start) / 2;addHelper(node->left, L, R, C);addHelper(node->right, L, R, C);node->sum = (node->left ? node->left->sum : 0) + (node->right ? node->right->sum : 0);}int queryHelper(SegmentTreeNode* node, int L, int R) {if (!node || node->end < L || node->start > R) {return 0;}if (node->start >= L && node->end <= R) {return node->sum;}int mid = node->start + (node->end - node->start) / 2;return queryHelper(node->left, L, R) + queryHelper(node->right, L, R);}public:SegmentTree(int n) {root = buildTree(vector<int>(n, 0), 0, n - 1);}void add(int L, int R, int C) {addHelper(root, L, R, C);}int query(int L, int R) {return queryHelper(root, L, R);}
};int main() {vector<int> nums = { 1,2,3,4,5,6,7,8,9,10 };SegmentTree st(nums.size());for (int i = 0; i < nums.size(); i++) {st.add(i, i, nums[i]);}cout << st.query(0, nums.size() - 1) << endl;cout << accumulate(nums.begin(), nums.end(), 0) << endl;cout << st.query(0, 5) << endl;cout << accumulate(nums.begin(), nums.begin() + 5 + 1, 0) << endl;return 0;
}

 

结尾
 

最后，感谢您阅读我的文章，希望这些内容能够对您有所启发和帮助。如果您有任何问题或想要分享您的观点，请随时在评论区留言。
 

 

同时，不要忘记订阅我的博客以获取更多有趣的内容。在未来的文章中，我将继续探讨这个话题的不同方面，为您呈现更多深度和见解。
 

 

谢谢您的支持，期待与您在下一篇文章中再次相遇！











http://www.ppmy.cn/news/1438582.html












相关文章










Docker网络模式与cgroup资源控制









Docker网络模式与cgroup资源控制




前言 
在 Docker 中&#xff0c;网络模式和 cgroup 资源控制作为关键功能&#xff0c;对于容器的性能优化和资源管理起着至关重要的作用。本文将介绍 Docker 的网络模式和cgroup资源控制&#xff0c;探讨不同网络模式的特点以及如何利用 cgroup 资源控制机制来有效管理容器的资…




阅读更多...

















【驱动】AM437x中出现很多bioset进程，杀不掉，有影响吗？









【驱动】AM437x中出现很多bioset进程，杀不掉，有影响吗？




1、问题描述 
查看linux系统进程时，发现很多bioset进程  
2、问题分析 
1）bioset进程是内核线程 这些bioset进程与Linux内核的块I/O（Block Input/Output）层有关，它们是内核线程，不是用户空间的进程。 
Linux的块I/O层负责管理磁盘和其他块设备的数据传输。当系统读写磁盘…




阅读更多...

















hcia datacom课程学习（7）：直连路由、静态路由









hcia datacom课程学习（7）：直连路由、静态路由




直连路由路由器接口上的网络&#xff08;接口配置了IP地址并且开启&#xff09;静态路由管理员手工添加的网络动态路由路由器之间动态学习形成的网络 
1.直连路由 
每当给路由器的一个接口配置了ip&#xff0c;路由表中就会产生对应的直连路由 
配置路由接口ip的命令&#xff1…




阅读更多...

















three.js 制作卡牌正反面 旋转









three.js 制作卡牌正反面 旋转




1.效果图 2.代码 
<template><div><div id"container"></div></div>
</template><script>
import * as THREE from "three";
import { OrbitControls } from "three/examples/jsm/controls/OrbitControls.…




阅读更多...

















python数据库操作（增删改查）









python数据库操作（增删改查）




添加数据 
import traceback
import pymysql
try:connect  pymysql.connect(user"root", password"123456", database"student", charset"utf8")corconnect.cursor()sql"insert into stu values(0,\未闻花名\,99.87);"cor.e…




阅读更多...

















C#中的浅拷贝（Shallow Copy）和深拷贝（Deep Copy），深拷贝的集中实现方式，浅拷贝深拷贝的案例









C#中的浅拷贝（Shallow Copy）和深拷贝（Deep Copy），深拷贝的集中实现方式，浅拷贝深拷贝的案例




C#中的浅拷贝&#xff08;Shallow Copy&#xff09;和深拷贝&#xff08;Deep Copy&#xff09; 
拷贝就是创建一个对象&#xff0c;这个对象有着原始对象数据&#xff08;属性和字段&#xff09;的一份精确拷贝&#xff08;只针对Object和Array这样的引用数据类型&#xff09;…




阅读更多...

















【JavaEE多线程】深入解析Java并发工具类与应用实践









【JavaEE多线程】深入解析Java并发工具类与应用实践




目录 JUC(java.util.concurrent)的常见类Callable 接口ReentrantLock原子类线程池ExecutorService 和 ExecutorsThreadPoolExecutor信号量 SemaphoreCountDownLatch 集合类多线程环境使用 ArrayList多线程环境使用队列多线程环境使用哈希表 JUC(java.util.concurrent)的常见类 …




阅读更多...

















Gateway网关跨域问题









Gateway网关跨域问题




一、模拟跨域问题 
通过vscode打开&#xff0c;模拟跨域问题的前端资料&#xff0c;在黑马视频中老师那个命令我似乎是不行的&#xff0c;应该是还没下载相关操作指令&#xff0c;但是可以通过下载一个插件来实现启动&#xff08;Live Server&#xff09;。 下载好后右键&#…




阅读更多...















 
 
 
 










最新文章







 





















Copyright @ 2022~2023