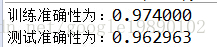写在前面：在前一篇文章，我分析了极限学习机的原理，包含比较详细的公式推导。
极限学习机原理（含公式推导透彻）
本篇文章主要介绍，在线式极限学习机。对于有样本数据不断增加和更新的场景，传统的极限学习机每次增加数据后都要重新把所有数据重新训练一遍，导致随着数据增多训练耗时越来越长。
在线式极限学习机，每次训练增加的样本数据即可，不用每次都把所有的数据重新训练一遍来获取模型。
PS：这里所有的逆矩阵，比如K^-1均是伪逆矩阵

一.原理推导

1.原理推导

在线顺序极限学习机分为两部分，第一部分初始学习阶段（形成一个初始的模型，相当于ELM）。第二部分在线学习部分即每次有更新的样本数据，将其加入模型中训练。
从ELM我们可以知道隐含层权值矩阵：β=H^-1T ′，这里的网络输出：T 如下
PS:T′为T的转置

（然后为了方便的推导在线式极限学习机）然后我们把T的形式稍微变一下，令T₀=T′，并且T
₀是一个行向量矩阵如下：

现在β=H^-1T₀，然后我们设H=H₀。令H₀=K^-1₀H^T₀，其中K₀=H^T₀H₀

我们知道elm希望求得使||H₀β-T₀||最小的β
而os-elm希望求得β⁽¹⁾使得下面这个二范数最小。

那么β⁽¹⁾的值为：

其中K₁为：

然后我们希望把β⁽¹⁾和β⁽⁰⁾关联起来上面的K₁可表示为，这样K0和K1的·关系就确定了

然后再说回β⁽¹⁾后面的H与T相乘的矩阵可以表示为：

那么可得到β⁽¹⁾与K₁、H₁、β⁽⁰⁾的递推关系

因此由公式01得到K的递推公式，由上面的公式02得到β的递推公式

下面的求逆矩阵，需要根据woodbury公式，下图是公式。就是说求了一个矩阵加法及乘法的逆矩阵
在我的博客中有提到Woodbury矩阵恒等式介绍

在在线学习的递推公式中，对应上面的公式C=E=I（单位矩阵），如下图

然后带入，woodbury公式

令P_k+1=K_k+1^-1 P_k=K_k^-1 ，则上面的公式可以表示为:

至此原理的推导就结束了。
这个P和β是我们每次训练的结果。P是在线式极限学习机的中间矩阵、β是隐含层输出矩阵。

2.对于样本按条更新的情况

对于一条一条样本更新的情况，上述公式会简化为：

  

如果您觉得本文写的不错，欢迎点赞评论收藏！