1049.最后一块石头的重量II
1049. 最后一块石头的重量 II - 力扣(LeetCode)
代码随想录 (programmercarl.com)
动态规划之背包问题,这个背包最多能装多少?LeetCode:1049.最后一块石头的重量II_哔哩哔哩_bilibili
有一堆石头,用整数数组
stones表示。其中stones[i]表示第i块石头的重量。每一回合,从中选出任意两块石头,然后将它们一起粉碎。假设石头的重量分别为
x和y,且x <= y。那么粉碎的可能结果如下:
- 如果
x == y,那么两块石头都会被完全粉碎;- 如果
x != y,那么重量为x的石头将会完全粉碎,而重量为y的石头新重量为y-x。最后,最多只会剩下一块 石头。返回此石头 最小的可能重量 。如果没有石头剩下,就返回
0。示例 1:
输入:stones = [2,7,4,1,8,1] 输出:1 解释: 组合 2 和 4,得到 2,所以数组转化为 [2,7,1,8,1], 组合 7 和 8,得到 1,所以数组转化为 [2,1,1,1], 组合 2 和 1,得到 1,所以数组转化为 [1,1,1], 组合 1 和 1,得到 0,所以数组转化为 [1],这就是最优值。示例 2: 输入:stones = [31,26,33,21,40] 输出:5提示:
1 <= stones.length <= 301 <= stones[i] <= 100
把石头尽量分成数值相等的两堆,相减的值才会最小。
本题物品的重量为stones[i],物品的价值也为stones[i]。
动规五部曲:
1、确定dp数组以及下标的含义:dp[j] 表示容量为j的背包,可以背的最大重量为dp[j];
2、确定递推公式:dp[j] = max(dp[j], dp[j - stones[i]] + stones[i]);
3、dp数组如何初始化:初始化一个长度为target+1的整形dp,用来存储动态规划中的结果:
int[] dp = new int[target + 1];4、确定遍历顺序:物品遍历的for循环在外,循环背包的for循环在内:
for (int i = 0; i < stones.length; i++) {// 内层循环从 target 开始,递减到 stones[i],采用倒序的方式。for (int j = target; j >= stones[i]; j--) {// 动态规划的状态转移方程,计算两种情况下的最大值:放入当前石头和不放入当前石头。dp[j] = Math.max(dp[j], dp[j - stones[i]] + stones[i]);}}5、举例推导dp数组:
输入[2,4,1,1], 此时target=4:
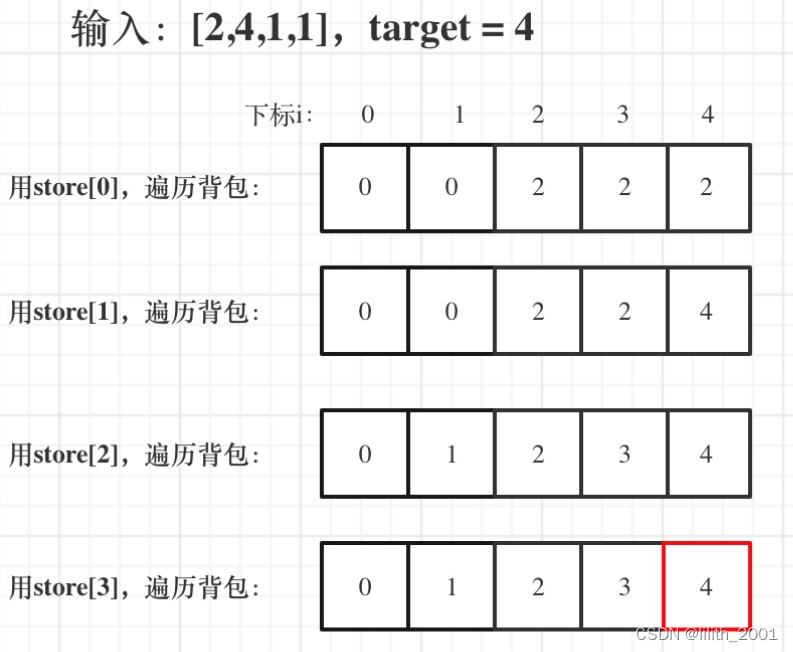
综合代码:
class Solution {// 定义一个公共方法,名称为 lastStoneWeightII,接受一个整型数组 stones,并返回一个整数。public int lastStoneWeightII(int[] stones) {// 初始化一个变量 sum,用于存储 stones 数组中所有元素的总和。int sum = 0;// 遍历 stones 数组,将所有元素的值累加到 sum 中。for (int i : stones) {sum += i;}// 将 sum 的值除以 2,并将结果赋给变量 target。int target = sum >> 1;// 初始化一个长度为 target + 1 的整型数组 dp,用于存储动态规划中的结果。int[] dp = new int[target + 1];// 使用两层循环来进行动态规划计算。for (int i = 0; i < stones.length; i++) {// 内层循环从 target 开始,递减到 stones[i],采用倒序的方式。for (int j = target; j >= stones[i]; j--) {// 动态规划的状态转移方程,计算两种情况下的最大值:放入当前石头和不放入当前石头。dp[j] = Math.max(dp[j], dp[j - stones[i]] + stones[i]);}}// 返回 stones 中所有元素的总和减去 2 倍的 dp[target]。return sum - 2 * dp[target];}
}
494. 目标和
1049. 最后一块石头的重量 II - 力扣(LeetCode)
代码随想录 (programmercarl.com)
动态规划之背包问题,装满背包有多少种方法?| LeetCode:494.目标和_哔哩哔哩_bilibili
有一堆石头,用整数数组
stones表示。其中stones[i]表示第i块石头的重量。每一回合,从中选出任意两块石头,然后将它们一起粉碎。假设石头的重量分别为
x和y,且x <= y。那么粉碎的可能结果如下:
- 如果
x == y,那么两块石头都会被完全粉碎;- 如果
x != y,那么重量为x的石头将会完全粉碎,而重量为y的石头新重量为y-x。最后,最多只会剩下一块 石头。返回此石头 最小的可能重量 。如果没有石头剩下,就返回
0。示例 1:
输入:stones = [2,7,4,1,8,1] 输出:1 解释: 组合 2 和 4,得到 2,所以数组转化为 [2,7,1,8,1], 组合 7 和 8,得到 1,所以数组转化为 [2,1,1,1], 组合 2 和 1,得到 1,所以数组转化为 [1,1,1], 组合 1 和 1,得到 0,所以数组转化为 [1],这就是最优值。示例 2:
输入:stones = [31,26,33,21,40] 输出:5提示:
1 <= stones.length <= 301 <= stones[i] <= 100
假设加法对应的总共和为x,那么减法对应的总和就是sum-x; 所以 x-(sum-x)=target;
x=(sum+target)/2; 此时就转化为:装满容量为x的背包,有几种方法。
之前遇到的都是01背包问题,在01背包问题中,物品都只能使用一次;而本题是装满有几种方法,是组合问题。
动规五部曲:
1、确定dp数组以及下标的含义:dp[j] 表示:填满j这么大容量的包,有dp[j]种方法;
2、确定递推公式:
dp[j] += dp[j - nums[i]]3、dp数组如何初始化:dp[0]=1;
4、确定遍历顺序:nums外循环,target内循环;
5、举例推导dp数组:
输入:nums: [1, 1, 1, 1, 1], S: 3
bagSize = (S + sum) / 2 = (3 + 5) / 2 = 4
dp数组状态变化如下:
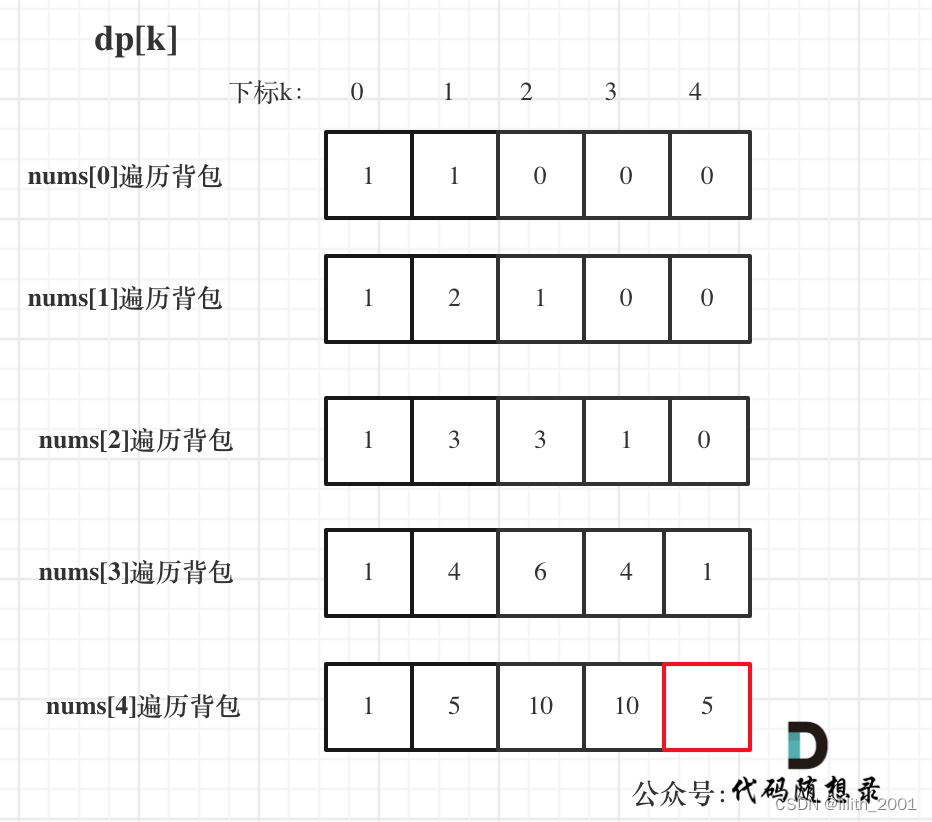
综合代码:
class Solution {// 定义一个公共方法,名称为 findTargetSumWays,接受一个整型数组 nums 和一个整数 target,并返回一个整数。public int findTargetSumWays(int[] nums, int target) {// 初始化一个变量 sum,用于存储 nums 数组中所有元素的总和。int sum = 0;for (int i = 0; i < nums.length; i++) sum += nums[i];// 如果 target 的绝对值大于 sum,那么是没有方案的,直接返回 0。if (Math.abs(target) > sum) return 0;// 如果 (target + sum) 除以 2 的余数不为 0,也是没有方案的,直接返回 0。if ((target + sum) % 2 == 1) return 0;// 计算背包的大小,即 (target + sum) 除以 2,这是动态规划的一个关键参数。int bagSize = (target + sum) / 2;// 初始化一个长度为 bagSize + 1 的整型数组 dp,用于存储动态规划中的结果。int[] dp = new int[bagSize + 1];// 初始时,背包容量为 0 的情况有一种方案,因此 dp[0] 初始化为 1。dp[0] = 1;// 使用两层循环进行动态规划计算。for (int i = 0; i < nums.length; i++) {// 内层循环从 bagSize 开始递减到 nums[i],采用倒序的方式。for (int j = bagSize; j >= nums[i]; j--) {// 动态规划的状态转移方程,计算两种情况下的方案数:放入当前元素和不放入当前元素。dp[j] += dp[j - nums[i]];}}// 返回背包容量为 bagSize 时的方案数。return dp[bagSize];}
}