南京邮电大学数学实验A 作业5 函数与方程答案 | 《MATLAB数学实验》第三版第四章课后习题答案

若要获得更好的阅读体验，请前往链接。

求点赞求点赞求点赞。

1(课本习题1)

求下列多项式的所有根，并验算：

(1) $x^{2} + x + 1$ ;

(2) $3x^{5} - 4x^{3} + 2x - 1$ ;

(3) $5x^{23} - 6x^{7} + 8x^{6} - 5x^{2}$ ;

(4) $2x + 3)^{3} - 4$ (提示: 先用conv展开)

代码：

matlab">function verify_roots(p, r, tol)% p: 多项式的系数向量,r: roots 函数的输出% tol: 误差容限all_passed = true;for i = 1:length(r)if abs(polyval(p, r(i))) > tolfprintf('根 %f + %fi 可能不准确\n', real(r(i)), imag(r(i)));all_passed = false;endendif all_passedfprintf('所有的根都已经通过验证，求根正确。\n');end
end% 1.1
tol = 1e-6; % 定义容差
p = [1 1 1];
r = roots(p)
verify_roots(p, r, tol)
% 1.2
p = [3 0 -4 0 2 -1];
r = roots(p)
verify_roots(p, r, tol)
% 1.3
p = zeros(1,24);
p([1 17 18 22]) = [5 -6 8 -5];
r = roots(p)
verify_roots(p, r, tol)
% 1.4
p1 = [2 3];
p2 = conv(p1,p1);
p3 = conv(p1,p2);
p3(end) = p3(end)-4;
r = roots(p3)
verify_roots(p3, r, tol)

输出：

ans =

-0.5000 + 0.8660i

-0.5000 - 0.8660i

所有的根都已经通过验证，求根正确。

ans =

-0.9479 + 0.3845i

-0.9479 - 0.3845i

1.0000 + 0.0000i

0.4479 + 0.3435i

0.4479 - 0.3435i

所有的根都已经通过验证，求根正确。

ans =

0.0000 + 0.0000i

0.0000 + 0.0000i

0.9768 + 0.0000i

0.9388 + 0.2682i

0.9388 - 0.2682i

0.8554 + 0.5363i

0.8554 - 0.5363i

0.6615 + 0.8064i

0.6615 - 0.8064i

0.3516 + 0.9878i

0.3516 - 0.9878i

-0.0345 + 1.0150i

-0.0345 - 1.0150i

-0.4609 + 0.9458i

-0.4609 - 0.9458i

-0.1150 + 0.8340i

-0.1150 - 0.8340i

-0.7821 + 0.7376i

-0.7821 - 0.7376i

-0.9859 + 0.4106i

-0.9859 - 0.4106i

-1.0416 + 0.0000i

-0.7927 + 0.0000i

所有的根都已经通过验证，求根正确。

ans =

-1.8969 + 0.6874i

-1.8969 - 0.6874i

-0.7063 + 0.0000i

所有的根都已经通过验证，求根正确。

2(课本习题2)

求方程 $x\ln{\left( \sqrt{x^{2} - 1} + x \right) - \sqrt{x^{2} - 1} - 0.5x = 0}$ 的正根。

代码：

matlab">Fun = @(x) x*log(sqrt(x^2-1)+x)-sqrt(x^2-1)-0.5*x;
% 使用fzero函数找到函数的零点
fzero(Fun,2)

输出：

ans = 2.1155

3(课本习题4)

(超越方程)超越方程的解有时是很复杂的，作出 $x\sin\frac{1}{x}$ 在[-0.1,
0.1]内的图，可见x=0附近 $f (x) = 0$ 有无穷多个解，并设法求出它们的近似解，是计算结果误差不超过0.01.

代码：

matlab">Fun = @(x) x.*sin(1/x);
% 使用fplot函数绘制函数图像
fplot(Fun, [-0.1 0.1]);
% 初始化零点数组
zeroPoints = zeros(1,10);
% 使用循环和fzero函数找到函数的零点
for idx=1:10zeroPoints(idx)=fzero(Fun,(idx-0.5)*0.01);
end
% 将正负零点合并
zeroPoints=[zeroPoints,-zeroPoints]

输出：

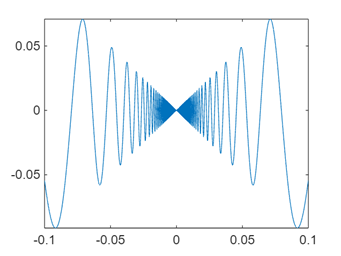
zeroPoints = 1×20

0.0050 0.0152 0.0245 0.0354 0.0455 0.0531 0.0637 0.0796 0.0796 0.1061 -0.0050 -0.0152 -0.0245 -0.0354 -0.0455 -0.0531 -0.0637 -0.0796 -0.0796 -0.1061

4(课本习题5)

求解下列非线性方程组在原点附近的根：

$KaTeX parse error: Expected '}', got '\right' at position 149: … \end{aligned} \̲r̲i̲g̲h̲t̲.\$

代码：

matlab">Fun = @(x) [9*x(1)^2+36*x(2)^2+4*x(3)^2-36;x(1)^2-2*x(2)^2-20*x(3);16*x(1)-x(1)^3-2*x(2)^2-16*x(3)^2];
% 使用fsolve函数求解非线性方程组
root = fsolve(Fun,[0 0 0]);
disp("求解到的根是")
disp(root)

输出：

求解到的根是

0.13416 0.99721 -0.098542

5(课本习题6)

求解下列方程组在区域 $\alpha,\ \beta < 1$ 内的解：

$KaTeX parse error: Expected '}', got '\right' at position 93: … b \end{array} \̲r̲i̲g̲h̲t̲.\$

代码：

matlab">求解到的根是0.13416      0.99721    -0.098542

输出：

求解到的根是

0.52652 0.50792

6(课本习题7)

(椭圆的交点)两个椭圆可能有0~4个交点，求下列两个椭圆的所有交点坐标：

$\begin{matrix} (x - 2)^{2} + (y - 3 + 2x)^{2} = 5, \\ 2(x - 3)^{2} + \left( \frac{y}{3} \right)^{2} = 4. \end{matrix}$

代码：

matlab">clear; close;
% 定义t的范围
t=0:pi/100:2*pi;
% 定义x1和y1
x1=2+sqrt(5)*cos(t);
y1=3-2*x1+sqrt(5)*sin(t);
% 定义x2和y2
x2=3+sqrt(2)*cos(t); 
y2=6*sin(t);
% 绘制图像，观察4个解的大致位置，然后分别求解
plot(x1,y1,x2,y2); grid on;
% 定义函数
fun = @(x) [(x(1)-2)^2+(x(2)-3+2*x(1))^2-5,2*(x(1)-3)^2+(x(2)/3)^2-4];
% 使用fsolve函数求解非线性方程组
sol1 = fsolve(fun,[1.5,2])
sol2 = fsolve(fun,[1.8,-2])
sol3 = fsolve(fun,[3.5,-5])
sol4 = fsolve(fun,[4,-4])

输出：

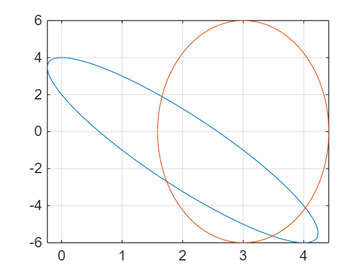
sol1 =

1.6581 1.8936

sol2 =

1.7362 -2.6929

sol3 =

3.4829 -5.6394

sol4 =

4.0287 -4.1171

7(课本习题8)

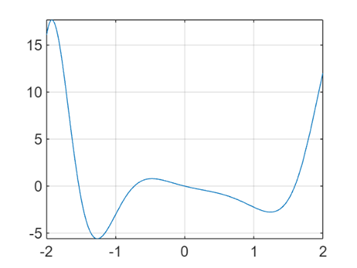
作出下列函数图形，观察所有的极大、极小和最大、最小值点的粗略位置；并用MATLAB函数fminbnd和
fminsearch求各极值点的确切位置:

(1) $f(x) = x^{2}\sin(x^{2} - x - 2)$ , [-2,2];

(2) $f(x) = 3x^{5} - 20x^{3} + 10$ , [-3,3];

(3) $f(x) = \|x^{3} - x^{2} - x - 2\|$ , [0,3].

代码：

matlab">% 题7.1
clear;clc;
% 求坐标的函数
function x1 = findRxtrmum(fun,x0,x0IsMaximum)for k =1:length(x0)%x1(k)=fzero(dfun,x0(k));continue;  % 导数法if x0IsMaximum(k)y = @(x) -fun(x);elsey = fun;end%x1(k)=fminbnd(y,x0(k)-0.3,x0(k)+0.3);  % fminbnd法x1(k)=fminsearch(y,x0(k));  % fminsearch法    end
end
% 可视化结果的函数
function plotExtremum(fun,x1,interval)x1 = sort([x1 interval]); % 将区间的端点添加到极值点中y1_values = fun(x1);% 将符号表达式转换为数值以进行计算[ymin, Imin] = min(y1_values);[ymax, Imax] = max(y1_values);% 计算原函数在极值点处的值figure;plot(x1, y1_values, 'k.', 'MarkerSize', 12);hold on;plot(x1(Imin), ymin, 'ro', 'MarkerSize', 8);plot(x1(Imax), ymax, 'bo','MarkerSize', 8);fplot(fun, interval,'LineWidth', 1.5);title('极值点');xlabel('x'); ylabel('y');legend('极值点','最小值点','最大值点','Location','best');grid on; hold off;%输出结果fprintf('极值点 (x):'); disp(x1);fprintf('极值 (y):'); disp(y1_values);fprintf('最小值点 (x, y):(%.4f, %.4f)\n', x1(Imin), ymin);fprintf('最大值点 (x, y):(%.4f, %.4f)\n', x1(Imax), ymax);
end% 定义函数
syms x
fun = @(x) x.^2.*sin(x.^2-x-2);
interval = [-2 2];
fun_sym = sym(fun);
dfun = matlabFunction(diff(fun_sym, x)); %导函数
fplot(dfun,interval); % 绘制导函数图像
grid on; % 根据图像观察极值点的大致位置
x0 = [-1.5 -0.75 0 1.5];
x0IsMaximum = [1 0 1 0];
x1 = findRxtrmum(fun,x0,x0IsMaximum);
plotExtremum(fun,x1,interval);
% 题7.2
clear;
syms x
fun = @(x) 3*x.^5-20*x.^3+10;
interval = [-3 3];
fun_sym = sym(fun);
dfun = matlabFunction(diff(fun_sym, x)); %导函数
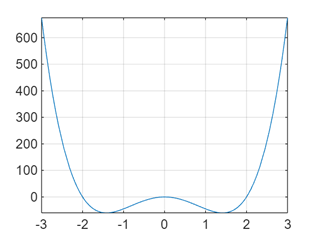
fplot(dfun,interval); % 绘制导函数图像
grid on; % 根据图像观察极值点的大致位置
x0 = [-2 2];
x0IsMaximum = [1 0];
x1 = findRxtrmum(fun,x0,x0IsMaximum);
plotExtremum(fun,x1,interval);
% 题7.3
clear;
syms x
fun = @(x) abs(x.^3-x.^2-x-2);
interval = [0 3];
fun_sym = sym(fun);
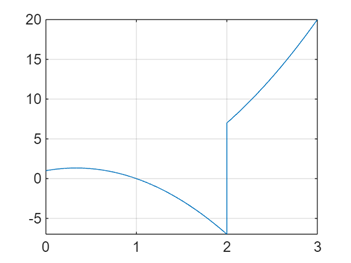
dfun = matlabFunction(diff(fun_sym, x)); %导函数
fplot(dfun,interval); % 绘制导函数图像
grid on; % 根据图像观察极值点的大致位置
x0 = [1 2];
x0IsMaximum = [1 0];
x1 = findRxtrmum(fun,x0,x0IsMaximum);
plotExtremum(fun,x1,interval);

输出：

极值点

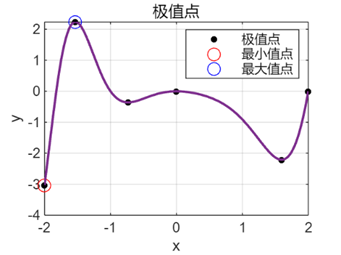
极值点 (x): -2.0000 -1.5326 -0.7315 0 1.5951 2.0000
极值 (y): -3.0272 2.2364 -0.3582 0 -2.2080 0
最小值点 (x, y): (-2.0000, -3.0272)
最大值点 (x, y): (-1.5326, 2.2364)

极值点

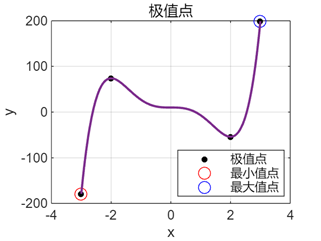
极值点 (x): -3 -2 2 3
极值 (y): -179 74 -54 199
最小值点 (x, y): (-3.0000, -179.0000)
最大值点 (x, y):(3.0000, 199.0000)

极值点

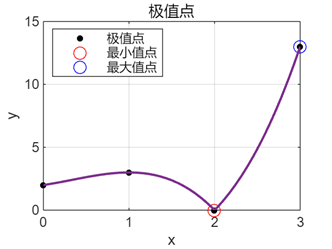
极值点 (x): 0 1 2 3
极值 (y): 2 3 0 13
最小值点 (x, y):(2.0000, 0.0000)
最大值点 (x, y):(3.0000, 13.0000)

8(课本习题12)

(月还款额)作为房产公司的代理人，你要迅速准确回答客户各方面的问题.现在有个客户看中了你公司一套建筑面积为180 $m^{2}$ ,每平方米单价75000元的房子.
他计划首付30%, 其余70%用20年按揭贷款(贷款年利率5.04%). 请你提供下列信息:
房屋总价格、首付款额、月还款额.
如果其中60万元为公积金贷款(贷款年利率4.05%)呢？

代码：

matlab">rate = 5.04/12/100; % 年利率
period = 20*12; % 贷款期数
totalHousePrice = 7500*180; % 房屋总价格
downPayment = totalHousePrice*0.3; % 首付款额
loanAmount = totalHousePrice - downPayment; % 贷款总额
% 月付还款额
monthlyPayment = (1+rate)^period*rate*loanAmount/((1+rate)^period-1);
fundInterestRate = 4.05/12/100; % 公积金贷款年利率
fundLoan = 60*10000; % 公积金贷款金额
% 公积金贷款的月付还款额
monthlyPayment1 = (1+fundInterestRate)^period*fundInterestRate*fundLoan/((1+fundInterestRate)^period-1);
% 商业贷款金额
commercialLoan = loanAmount - fundLoan;
% 商业贷款的月付还款额
monthlyPayment2 = (1+rate)^period*rate*commercialLoan/((1+rate)^period-1);
% 总的月付还款额
totalMonthlyPayment = monthlyPayment1 + monthlyPayment2;
fprintf("房屋总价格:%4.2f、首付款额:%4.2f、月还款额:%4.2f",totalHousePrice, downPayment, monthlyPayment)
fprintf("如果其中60万元为公积金贷款，月还款额为%4.2f",totalMonthlyPayment)

输出：

房屋总价格:1350000.00、首付款额:405000.00、月还款额:6257.48

如果其中60万元为公积金贷款，月还款额为5936.19

9(课本习题13)

(拴牛鼻的绳子)农夫老李有一个半径为10m的圆形牛栏，里面长满了草，老李要将家里一头牛拴在一根栏桩上，但只让牛吃到一半草，他想让
上大学的儿子告诉他，拴牛鼻的绳子应为多长？

代码：

matlab">%根据条件列方程theta*R^2+(pi-2*theta)*r^2-R*r*sin(theta)=pi*r^2/2
%化简得sin(2*theta)-2*theta*cos(2*theta)=pi/2
% 定义函数
fun = @(theta) sin(2*theta) - 2*theta*cos(2*theta) - pi/2;
th = fsolve(fun, pi/4);
% 计算R的值
R = 20*cos(th)

输出：

R =
11.587

10(课本习题14)

(弦截法)Newton迭代法是一种速度很快的迭代方法，但是它需要预先求得导函数.
若用差商代替导数，则可得下列弦截法

$x_{k + 1} = x_{k} - \frac{x_{k} - x_{k - 1}}{f\left( x_{k} \right) - f\left( x_{k - 1} \right)}f\left( x_{k} \right).$

这一迭代法需要两个初值 $x_{0},x_{1}$ ,编写一个通用的弦截法计算机程序并用以解:
$x\ln{\left( \sqrt{x^{2} - 1} + x \right) - \sqrt{x^{2} - 1} - 0.5x = 0}$

代码：

matlab">% 定义弦截法函数
function root = secantMethod(func, x0, x1, tol)while abs(x0-x1) > tolroot = x1 - (x1-x0)*feval(func, x1)/(feval(func, x1) - feval(func, x0));x0 = x1;x1 = root;end
end% 定义函数
fun = @(x) x*log(sqrt(x^2-1)+x) - sqrt(x^2-1) - 0.5*x;
% 使用割线法求解
secantMethod(fun, 1, 2, 1e-8)

输出：

ans = 2.1155

11

采用二分法计算 $x\cos x - 2 = 0$ ，查找区间为 $\in$ [-4, 2].

代码：

matlab">% 定义函数
f = @(x) x.*cos(x) - 2;
function root = dichotomy(f, a, b, tol, n)%f: 要求解的函数句柄;a,b: 初始区间,要求f(a)* f(b) <0% tol: 误差容限;n: 最大选代次数if f(a)* f(b)>= 0error('初始区间不满足二分法条件');ends = 0;while abs(b - a) > tol && s < n; c =(a + b) / 2;if f(c) == 0; root = c; return;endif f(a) * f(c) < 0; b = c; else; a = c; end; s = s + 1;endif s == n; warning('达到最大迭代次数，可能未找到精确解'); endroot=(a +b)/2;% 返回区间的中点作为近似解
end% 使用二分法找到零点
x_solution = dichotomy(f, -4, 2, 1e-6, 1000);
% 打印结果
fprintf('方程的解是%f\n', x_solution);

输出：

方程的解是-2.498756

12

用两种迭代方法寻找 $x^{3} + 4x^{2} - 10 = 0$ 在区间[1, 2]的一个根。

代码：

matlab">% 定义函数和它的导数
f = @(x) x^3 + 4*x^2 - 10;
df = @(x) 3*x^2 + 8*x;a = 1; b = 2; % 定义区间
tol = 1e-6; % 定义容差
n = 1000; % 最大迭代次数% 牛顿法
function root = newton(f, df, x, tol, n)% f: 要求解的函数句柄, df: 函数f的导数的句柄% x: 初始估计值, tol: 误差容限, n: 最大迭代次数s = 0;while abs(f(x)) > tol && s < nx = x - f(x)/df(x);s = s + 1;endif s == nwarning('达到最大迭代次数，可能未找到精确解');endroot = x; % 返回近似解
end
root = newton(f, df, (a+b)/2, tol, n);
fprintf('牛顿法：%f\n', root);% 二分法
function root = bisection(f, a, b, tol, n)%f: 要求解的函数句柄;a,b: 初始区间,要求f(a)* f(b) <0% tol: 误差容限;n: 最大选代次数if f(a)* f(b)>= 0error('初始区间不满足二分法条件');ends = 0;while abs(b - a) > tol && s < n; c =(a + b) / 2;if f(c) == 0; root = c; return;endif f(a) * f(c) < 0; b = c; else; a = c; end; s = s + 1;endif s == n; warning('达到最大迭代次数，可能未找到精确解'); endroot=(a +b)/2;% 返回区间的中点作为近似解
end
root = bisection(f, a, b, tol, n)
fprintf('二分法：%f\n', root);