图论基础知识
学习记录自代码随想录
dfs 与 bfs 区别
dfs是沿着一个方向去搜,不到黄河不回头,直到搜不下去了,再换方向(换方向的过程就涉及到了回溯)。
bfs是先把本节点所连接的所有节点遍历一遍,走到下一个节点的时候,再把连接节点的所有节点遍历一遍,搜索方向更像是广度,四面八方的搜索过程。
深度优先搜索理论(Depth First Search, 简称DFS)
搜索方向,是认准一个方向搜,直到碰壁之后再换方向
换方向是撤销原路径,改为节点链接的下一个路径,回溯的过程。
回溯算法模板
// 1.确定返回值和参数
void backtracking(参数){// 2.确定回溯终止条件if(终止条件){// 存放结果;return; }// for横向遍历for(选择:本层集合中元素(树种节点孩子的数量就是集合的大小)){处理节点;// 纵向遍历backtracking(路径,选择列表); // 递归回溯,撤销处理结果}
}
回溯算法模板,其实就是dfs框架
// 1.确定递归函数返回值和参数,一般无返回值
一般情况下深搜需要二维数组结构保存所有路径,需要一维数组保存单一路径,
可定义全局变量
vector<vector<int>> result; // 保存符合条件的所有路径
vector<int> path; // 起点到终点的路径
void dfs(参数){// 2.确定回溯终止条件if(终止条件){// 存放结果;return; }// 3.处理目前节点出发的路径// for横向遍历for(选择:本节点所连接的其他节点){处理节点;// 纵向遍历dfs(图,选择的节点); // 递归回溯,撤销处理结果}
}
广度优先搜索(Breath First Search, 简称BFS)
广搜的使用场景
广搜的搜索方式就适合于解决两个点之间的最短路径问题。
因为广搜是从起点出发,以起始点为中心一圈一圈进行搜索,一旦遇到终点,记录之前走过的节点就是一条最短路。
当然,也有一些问题是广搜 和 深搜都可以解决的,例如岛屿问题,这类问题的特征就是不涉及具体的遍历方式,只要能把相邻且相同属性的节点标记上就行。 (我们会在具体题目讲解中详细来说)
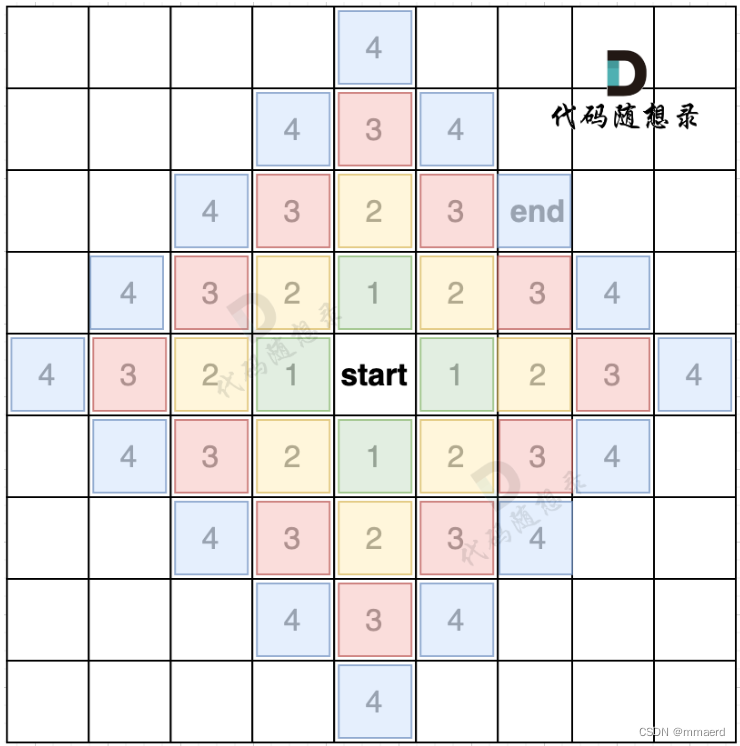
正是因为BFS一圈一圈的遍历方式,所以一旦遇到终止点,那么一定是一条最短路径。
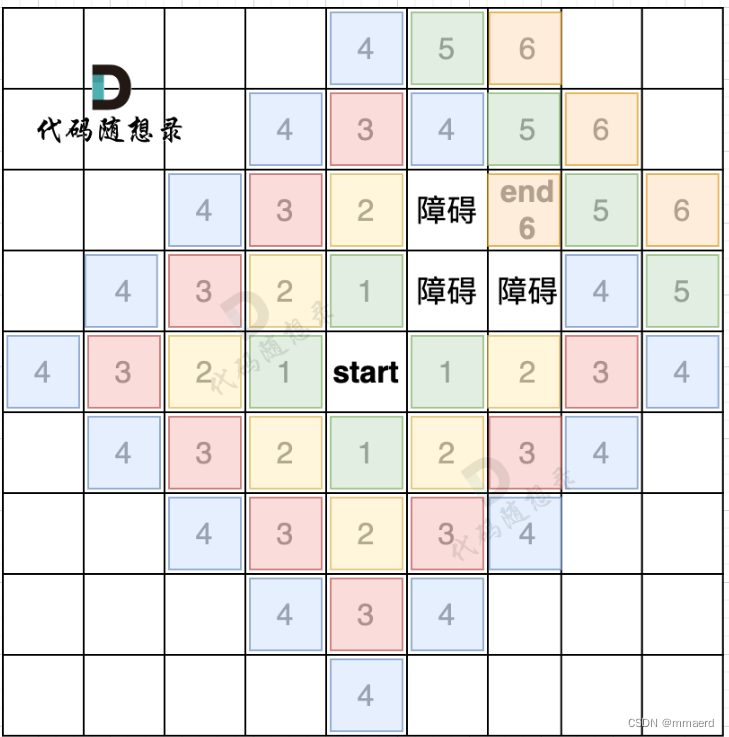
广搜代码模板(针对四方格地图)
int dir[4][2] = {0, 1, 1, 0, -1, 0, 0, -1}; // 表示四个方向
// grid为二维数组,地图
// visited标记访问过的节点
void bfs(vector<vector<char>>& grid, vector<vector<bool>>& visited, int x, int y){que<pair<int, int>> que; // 定义队列que.push({x,y}); // 起始点加入队列visited[x][y] = true; // 只要加入队列,立刻标记为访问过的节点while(!que.empty()){pair<int, int> cur = que.front();que.pop(); // 从队列种取元素int cur_x = cur.first;int cur_y = cur.second;for(int i = 0; i < 4; i++){ // 从开始节点的四个方向上右左下遍历// 获取周边四个节点坐标int next_x = cur_x + dir[i][0];int next_y = cur_y + dir[i][1]; // 坐标越界直接跳过if(next_x < 0 || next_x >= grid.size() || next_y < 0 || next_y >= grid.size()){continue;}// 若节点未被访问过if(!visited[next_x][nenxt_y]){// 队列添加新节点供下一轮遍历que.push({next_x, next_y});// 只要加入队列,代表被访问过,进行标记,防止重复访问visited[next_x][next_y] = true; }}}
}
例题:华为20240410机考
//第二题 会议通知转发总人数
//在一个办公区内,有一些正在办公的员工,当员工A收到会议通知,
//他会将这个会议通知转发给周围四邻(上下左右工位的同事)团队内的同事,
//周围收到该邮件的同事会继续转发给周围四邻(上下左右工位的同事团队内的同事,
//直到周围没有再需要往下传播的同事则会停止;同时此扩散还有前提条件,给定一可收到该邮件的团队列表relations,
//扩散时若该同事所在团队在relations列表中,则可进行扩散,否则不可进行扩散。
//办公室用一个二维数组office表示,其中office[i][j]表示该同事的团队名称,
//其中团队名称用整数t范围内的数字表示,i,j表示该同事的工位位置。
//
//现给定办公区的工位总行数与每一行的具体工位人员分布以及收到会议通知员工A的工位位置的坐标位置i,j :
//还有与该邮件关联的团队编号列表relations, 请分析得出最终会有多少同事收到该会议的转发通知。
//
//注意:1、该办公区位置用二维数组表示,该二维数组以左上角的工位为起点(0, 0),
//按照横轴向右纵轴向下的方向展开;原始收到会议通知的员工A不包含在总人数中。
//2、扩散时若该同事与收到初始收到邮件的员工A属于同一团队,
//若该团队名不在可收到通知的团队列表relations中,依然不可收到该邮件转发//输入
//第一行是一个整数n, 表示该办公区共有多少排,即就是office.length
//第二行是一个整数m, 标识该办公区共有多少列,即就是offce[i].length
//接下来n行表示每一排员工的具体分布情况,每个工位上的员工所在的团队号x用空格隔开
//接下来一行是两个数字用空格隔开,表示收到会议通知员工的工位位置,i表示横坐标位置,j表示纵坐标位置
//最后一行是一个字符串,表示可收到该邮件的团队列表relations, 团队名称之间用空格隔开
//提示:
//0 <= i <= 1000
//0 <= j <= 1000
//1 <= t <= 50
//1 <= relations.length <= 50//输出
//输出收到转发会议通知的总人数。//样例输入1
//5
//5
//1 3 5 2 3
//2 2 1 3 5
//2 2 1 3 3
//4 4 1 1 1
//1 1 5 1 2
//2 2
//1
//样例输出1
//5//样例输入2
//2
//2
//1 1
//2 2
//0 0
//2
//样例输出2
//2#include <iostream>
#include <vector>
#include <string>
#include <sstream>
#include <queue>
#include <algorithm>using namespace std;class Solution {
public:int getmaxNum(vector<vector<int>>& office, vector<vector<bool>>& visited, int i, int j, vector<int>& relations) {int dir[4][2] = { 0, 1, 1, 0, -1, 0, 0, -1 };int cnt = 0;queue<pair<int, int>> que;que.push({ i, j });visited[i][j] = 1;while (!que.empty()){auto cur = que.front();que.pop();int cur_x = cur.first, cur_y = cur.second;for (int k = 0; k < 4; k++) {int next_x = cur_x + dir[k][0];int next_y = cur_y + dir[k][1];if (next_x < 0 || next_x >= office.size() || next_y < 0 || next_y >= office[0].size()) continue;if (!visited[next_x][next_y] && (find(relations.begin(), relations.end(), office[next_x][next_y]) != relations.end())) {que.push({ next_x, next_y });visited[next_x][next_y] = true;cnt++;}}}return cnt;}
};int main() {int n;cin >> n;cin.ignore();int m;cin >> m;// cin >> m;后直接调用getline, 相当于读取了一个换行符'\n'cin.ignore();vector<vector<int>> office(n);for (int i = 0; i < n; i++) {string line;getline(cin, line);istringstream iss(line);int k;while (iss >> k) {office[i].push_back(k);}}int i, j;cin >> i >> j;cin.ignore();string s;getline(cin, s);vector<int> relations;istringstream iss(s);int temp;while (iss >> temp) {relations.push_back(temp);}vector<vector<bool>> visited(n, vector<bool>(m, false));Solution sol;int result = sol.getmaxNum(office, visited, i, j, relations);cout << result;return 0;
}