鸢尾花数据集的KNN探索与乳腺癌决策树洞察
今天博主做了这个KNN和决策树的实验。
一.数据集介绍
介绍一下数据集:
威斯康星州乳腺癌数据集:
威斯康星州乳腺癌数据集(Wisconsin Breast Cancer Dataset)是一个经典的机器学习数据集,它最初由威斯康星州医院的Dr. William H. Wolberg收集。这个数据集被广泛用于分类任务、特征选择、模型评估等机器学习任务和实验中 数据类型:这是一份多变量数据集,包含了乳腺癌的生理参数。
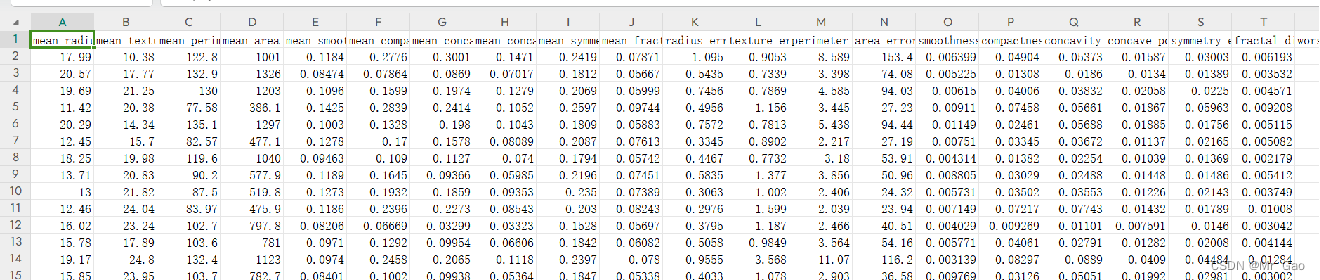
数据集特征:
特征:数据集由 30 个特征组成,这些特征是图像分析得到的,包括纹理、面积、平滑度、凸性、颗粒度等统计参数。
目标变量:数据集的目标变量是二分类的,即是否患有乳腺癌,用 0 和 1 表示。
样本数量:数据集包含 569 个样本。
鸢尾花数据集
鸢尾花数据集最初由Edgar Anderson测量得到,而后在著名的统计学家和生物学家R.A Fisher于1936年发表的文章中被引入到统计和机器学习领域数据集特征:
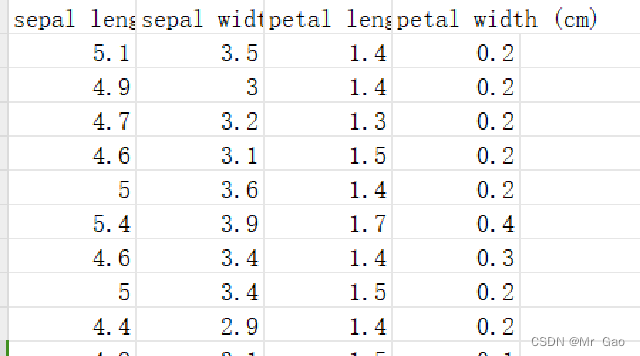
鸢尾花数据集包含了150个样本,每个样本有4个特征,这些特征是从花朵的尺寸测量中得到的,具体包括:
花萼长度(sepal length):在厘米单位下的花朵萼片的长度。
花萼宽度(sepal width):花萼片的宽度。
花瓣长度(petal length):花瓣的长度。
花瓣宽度(petal width):花瓣的宽度。
看一下我们的代码:
决策树代码:
from sklearn.datasets import load_breast_cancer
import matplotlib.pyplot as plt
import pandas as pd
breast_cancer=load_breast_cancer()
from sklearn.tree import plot_tree
#df = pd.DataFrame(breast_cancer.target, columns=breast_cancer.feature_names)
#df.to_csv(r'D:\coursework\maching_learning\breast_cancer.csv', index=None)
#print(type(breast_cancer))#df = pd.DataFrame(breast_cancer.target, columns="label")
#df.to_csv(r'D:\coursework\maching_learning\breast_cancer_label.csv', index=None)
#print(type(breast_cancer))print('breast_cancer数据集特征')
print(breast_cancer.data[:5])
print('breast_cancer数据集标签')
print(breast_cancer.target[:5])#2.进行数据集分割。from sklearn.model_selection import train_test_split
data_train,data_test,target_train,target_test=train_test_split(breast_cancer.data,breast_cancer.target,test_size=0.2)#3.配置决策树模型。
from sklearn import tree # 导入决策树包
clf = tree.DecisionTreeClassifier() #加载决策树模型
#4.训练决策树模型。
clf.fit(data_train, target_train)#5.模型预测。
predictions = clf.predict(data_test) # 模型测试
predictions[:10]
#6.模型评估。
from sklearn.metrics import accuracy_score # 导入准确率评价指标
print('Accuracy:%s'% accuracy_score(target_test, predictions))#7.参数调优。可以根据评估结果,对模型设置或调整为更优的参数,使评估结果更准确。
#信息增益--entropy
criterions=['gini','entropy']
for ct in criterions:clf2 = tree.DecisionTreeClassifier(criterion = ct)clf2.fit(data_train, target_train)plot_tree(clf2,filled=True, class_names=breast_cancer.target_names,label=ct)predictions2 = clf2.predict(data_test) # 模型测试# print('第一种:采用信息增益后的Accuracy:%s'% accuracy_score(target_test, predictions2))#最大深度--max_depthimport numpy as npmax_depths = np.linspace(1, 32, 32, endpoint=True)scores=[]for i in max_depths:clf3 = tree.DecisionTreeClassifier(max_depth=i)clf3.fit(data_train, target_train)predictions3 = clf3.predict(data_test) # 模型测试scores.append(accuracy_score(target_test,predictions3))import matplotlib.pyplot as pltplt.figure()plt.plot(scores)plt.title('max_depth-accuracy_score,'+"criterion = "+ct)plt.xlabel('max_depth')plt.ylabel('accuracy_score')plt.show()max_score_index=np.argmax(scores)+1print('可见当max-depth=',max_score_index,'时为最优其准确率为:',scores[max_score_index-1])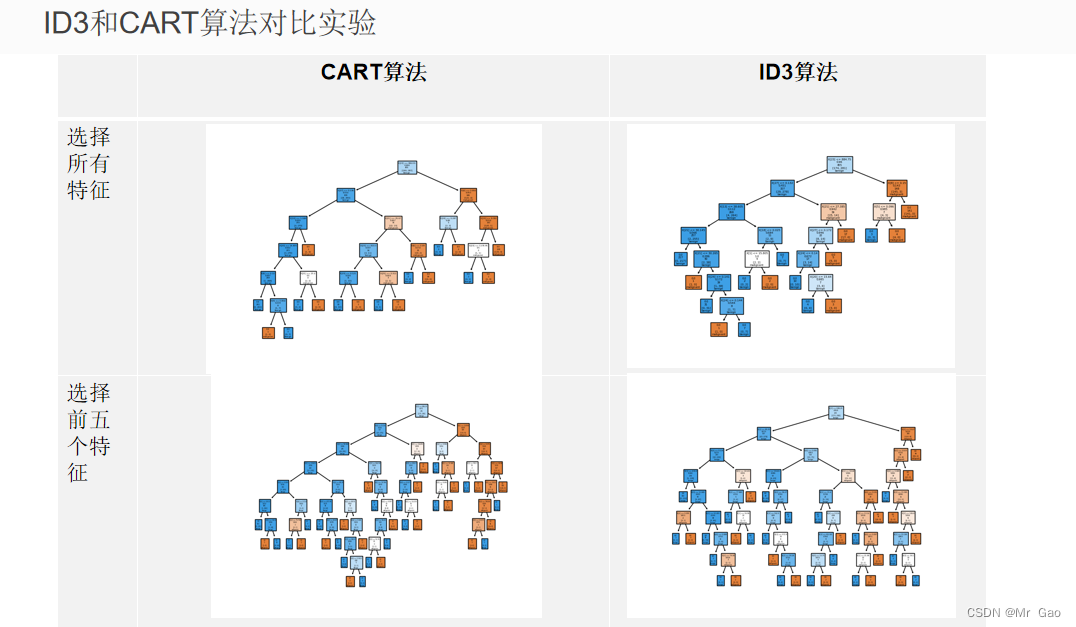
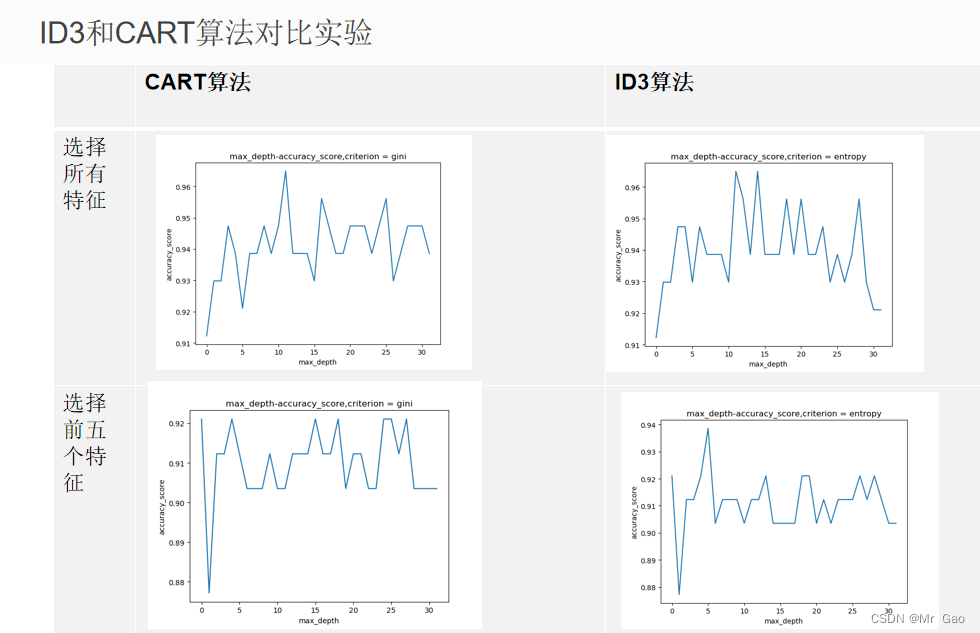
后剪枝与预剪枝代码:
import math
import pandas as pd
import matplotlib.pyplot as plt
# 设置中文显示字体
from pylab import mpl
import copy
mpl.rcParams["font.sans-serif"] = ["SimHei"]# 使用文本注释绘制树节点
decision_node = dict(boxstyle='sawtooth', fc='0.8')
leaf_node = dict(boxstyle='round4', fc='0.8')
arrow_args = dict(arrowstyle='<-')# 节点
def plotNode(nodeTxt, centerPt, parentPt, nodeType):createPlot.ax1.annotate(nodeTxt, xy=parentPt, xycoords='axes fraction',xytext=centerPt, textcoords='axes fraction',va="center", ha="center", bbox=nodeType, arrowprops=arrow_args)# 获取叶节点的数目
def getNumLeafs(my_tree):num_leafs = 0first_str = list(my_tree.keys())[0]second_dict = my_tree[first_str]for key in second_dict.keys():if type(second_dict[key]).__name__ == 'dict':num_leafs += getNumLeafs(second_dict[key])else:num_leafs += 1return num_leafs# 获取树的深度
def getTreeDepth(my_tree):max_depth = 0first_str = list(my_tree.keys())[0]second_dict = my_tree[first_str]for key in second_dict.keys():if type(second_dict[key]).__name__ == 'dict':this_depth = 1 + getTreeDepth(second_dict[key])else:this_depth = 1if this_depth > max_depth:max_depth = this_depthreturn max_depth# 绘制树中文本
def plotMidText(cntr_pt, parent_pt, txt_string):x_mid = (parent_pt[0] - cntr_pt[0]) / 2.0 + cntr_pt[0]y_mid = (parent_pt[1] - cntr_pt[1]) / 2.0 + cntr_pt[1]createPlot.ax1.text(x_mid, y_mid, txt_string)# 绘制树
def plotTree(my_tree, parent_pt, node_txt):num_leafs = getNumLeafs(my_tree)depth = getTreeDepth(my_tree)first_str = list(my_tree.keys())[0]cntr_pt = (plotTree.x_off + (1.0 + float(num_leafs)) / 2.0 /plotTree.total_w, plotTree.y_off)plotMidText(cntr_pt, parent_pt, node_txt)plotNode(first_str, cntr_pt, parent_pt, decision_node)second_dict = my_tree[first_str]plotTree.y_off = plotTree.y_off - 1.0 / plotTree.total_dfor key in second_dict.keys():if type(second_dict[key]).__name__ == 'dict':plotTree(second_dict[key], cntr_pt, str(key))else:plotTree.x_off = plotTree.x_off + 1.0 / plotTree.total_wplotNode(second_dict[key], (plotTree.x_off, plotTree.y_off), cntr_pt, leaf_node)plotMidText((plotTree.x_off, plotTree.y_off), cntr_pt, str(key))plotTree.y_off = plotTree.y_off + 1.0 / plotTree.total_ddef createPlot(in_tree,method):# 新建一个窗口fig = plt.figure(1, facecolor='white')# 清除图形fig.clf()axprops = dict(xticks=[], yticks=[])# 创建子图createPlot.ax1 = plt.subplot(111, frameon=False, **axprops)# w为决策树叶子个数plotTree.total_w = float(getNumLeafs(in_tree))# d为决策树深度plotTree.total_d = float(getTreeDepth(in_tree))plotTree.x_off = -0.5 / plotTree.total_wplotTree.y_off = 1.0plotTree(in_tree, (0.5, 1.0), '')# 显示try:plt.title("method="+method,pad=15)except:plt.title("method=None",pad=15)plt.show()def readDataset(): '''读取csv格式的数据集,返回dataset与labels的list形式''' #数据集内有中文字符,读取csv文件时需要使用gbk方式读取df = pd.read_csv('data.csv',encoding="utf8")#前14个样本作为训练集,后4个样本作为验证集trainDf = df.loc[0:350]testDf = df.loc[350:]#labels为该df的列labels = df.columns.tolist()#训练集以及测试集为对应df的值trainDataset = trainDf.values.tolist()testDataset = testDf.values.tolist()return trainDataset, testDataset, labelsdef Entropy(dataset):'''计算信息熵并返回'''# 样本个数numExamples = len(dataset)# 类别计数器classCount = {}# 每个样本的最后一列为刚样本所属的类别,循环每个样本,以每个类别为key,对应的value# 就是该类别拥有的样本数for example in dataset:# example[-1]就为样本的类别# 如果类别对应的key不存在就创建对应的key,样本数(value)置0if example[-1] not in classCount.keys():classCount[example[-1]] = 0 # 将类别计数器当中的对应类别的样本数(value) + 1classCount[example[-1]] += 1 # 熵的计算公式为: entropy = pi * log2(pi)entropy = 0.0 for num in classCount.values():# 样本出现概率 = 样本出现次数 / 样本总数p = num / numExamplesentropy -= p * math.log(p,2)return entropydef majorityCnt(classList): '''统计每个类别的个数,返回出现次数多的类别'''# 类别计数器classCount={}for c in classList:if c not in classCount.keys():classCount[c] = 0classCount[c] += 1# reverse = True 从大到小排列,key x[1]指比较key、value中的valuesortedClassCount = sorted(classCount.items(),key=lambda x:x[1],reverse=True)return sortedClassCount[0][0]def splitDataset(dataset, index, splitValue):'''划分数据集index : 该特征的索引splitValue : 每次取第i个样本与第i+1个样本的第index个特征的平均值splitValue作为数据集划分点,返回子集1与子集2'''subDataset1 = []subDataset2 = []# 遍历每个样本,当样本中的第index列的值<splitValue时,归为子集1# 当样本中的第index列的值>splitValue时,归为子集2for example in dataset:if example[index] <= splitValue:# 取出分裂特征前的数据集splitFeature = example[:index] # 取出分裂特征后的数据集,并合并splitFeature.extend(example[index+1:]) # 本行取得的去除example中index列的列表,加入总列表subDataset1.append(splitFeature) else:# 取出分裂特征前的数据集splitFeature = example[:index] # 取出分裂特征后的数据集,并合并splitFeature.extend(example[index+1:]) # 本行取得的去除example中index列的列表,加入总列表subDataset2.append(splitFeature) return subDataset1, subDataset2def chooseBestFeatureToSplit(dataset):'''返回最优特征索引和最佳划分点值'''# 特征数,由于最后一列是类别不是特征,将最后一列去掉numFeatures = len(dataset[0]) - 1 # 计算原始信息熵baseEntropy = Entropy(dataset) # 信息增益bestInfoGain = 0 # 最优特征下标bestIndex = -1 # 最佳划分点bestSplitValue = 0for column in range(0, numFeatures):# 取出第i列特征值featureList = [example[column] for example in dataset]# 排序featureList = sorted(featureList)# 使用第column列特征值的第row行和第row+1行的平均值作为划分点,进行划分# 得到左右两个子集for row in range(0,len(featureList)-1): newEntropy = 0splitValue = (featureList[row] + featureList[row + 1]) / 2.0 subDataset1, subDataset2 = splitDataset(dataset,column,splitValue)# 权重 = 子集样本数 / 全集样本数weight1 = len(subDataset1) / float(len(dataset))weight2 = len(subDataset2) / float(len(dataset))# 按某个特征分类后的熵 = (子集的熵 * 子集占全集的比重) 的总和newEntropy += weight1 * Entropy(subDataset1) newEntropy += weight2 * Entropy(subDataset2)# 信息增益 = 原始熵 - 按某个特征分类后的熵infoGain = baseEntropy - newEntropy# 更新信息增益与对应最佳特征的索引if infoGain > bestInfoGain: bestInfoGain = infoGainbestIndex = columnbestSplitValue = splitValuereturn bestIndex, bestSplitValuedef createTree(trainDataset, testDataset, labels, method = None):'''method 为 [None, 'pre', 'post']中的一种None为不使用剪枝操作,'pre'为使用预剪枝操作,'post'为使用后剪枝操作,递归建树1.获取最佳特征索引bestIndex以及最佳划分点bestSplitValue2.根据bestIndex和bestSplitValue将训练集与测试集划分为左右两个子集subDataset1和subDataset23.如选择预剪枝,则每次衡量划分子集前的精确度和划分子集后的精确度,如有提高才生成子树;4.如选择后剪枝,则先生成子树,再衡量去除每个子树是否带来精确度的提高,如有提高则去除子树;返回值:1.method为None或'pre'时,返回myTree2.method为'post'时,返回myTree与correct注意:这个correct是指由训练集划分出的子树对测试集进行预测,一共预测对多少个样本的个数。'''# 获取训练集与测试集当中的所有类别trainClassList = [example[-1] for example in trainDataset] testClassList = [example[-1] for example in testDataset]#print(trainClassList)# 若训练集中只有一个类时,有两种情况:# 1.如果当前采用后剪枝,则返回predict_class与correct# 2.如果不剪枝或采用预剪枝,则返回predict_classif trainClassList.count(trainClassList[0]) == len(trainClassList):# 当前子树预测类别predict_class = trainClassList[0]# 当前预测类别预测测试集对的个数correct = testClassList.count(predict_class)if method == 'post':return predict_class, correctelse: return predict_class# 若训练集最后只剩下类别,有两种情况:# 1.如果当前采用后剪枝,则返回predict_class与correct# 2.如果不剪枝或采用预剪枝,则返回predict_classif len(trainDataset[0]) == 1: # 当前子树预测类别predict_class = majorityCnt(trainClassList)# 当前预测类别预测测试集对的个数correct = testClassList.count(predict_class)if method == 'post':return predict_class, correctelse: return predict_class# 找到当前情况下使训练集信息增益最大的特征的索引,以及最佳的划分点值bestIndex, bestSplitValue = chooseBestFeatureToSplit(trainDataset) # print(bestIndex)print(labels[bestIndex])# 最优特征的名字bestFeature = labels[bestIndex]# 创建决策树 myTree = {bestFeature:{}}# 从labels中删除最优特征#del(labels[bestIndex])# 使用最优特征索引与最佳参数划分出训练集与测试集的两个子集trainSubDataset1, trainSubDataset2 = splitDataset(trainDataset,bestIndex,bestSplitValue)testSubDataset1, testSubDataset2 = splitDataset(testDataset,bestIndex,bestSplitValue)# 获取训练集与测试集中子集1与子集2的所有类别trainSubClassList1 = [example[-1] for example in trainSubDataset1] trainSubClassList2 = [example[-1] for example in trainSubDataset2] testSubClassList1 = [example[-1] for example in testSubDataset1] testSubClassList2 = [example[-1] for example in testSubDataset2] if method == 'pre':# 划分子集前:# 预测类别为当前训练集中最多的类别predict_class_pre = majorityCnt(trainClassList)# 使用训练集中最多的类别预测当前未划分的测试集的准确度precision_pre = testClassList.count(predict_class_pre)/len(testClassList)# 划分子集后:# 子集1的预测类别为当前训练子集1中最多的类别,子集2同理predict_class_post1 = majorityCnt(trainSubClassList1)predict_class_post2 = majorityCnt(trainSubClassList2)# 使用这两个类别分别预测测试集的子集1与子集2的正确总数correct1 = testSubClassList1.count(predict_class_post1)correct2 = testSubClassList2.count(predict_class_post2)totalCorrect = correct1 + correct2# 划分子集后的准确率precision_post = totalCorrect / len(testClassList)print("precision_post",precision_post)print("precision_pre",precision_pre)# 如果划分子集后的准确率比划分前更高,则划分子集,否则返回当前样本中最多的类别if precision_post > precision_pre:myTree[bestFeature]["<="+str(bestSplitValue)] = createTree(trainSubDataset1,testSubDataset1, labels, method = 'pre')myTree[bestFeature][">"+str(bestSplitValue)] = createTree(trainSubDataset2,testSubDataset2, labels, method = 'pre')else:return predict_class_preelif method == 'post':# 剪枝前:predict_class_pre = majorityCnt(trainClassList)# 生成leftTree与rightTree并得到该子树预测测试集对的数量correct1与correct2leftTree, correct1 = createTree(trainSubDataset1,testSubDataset1, labels, method = 'post')rightTree, correct2 = createTree(trainSubDataset2,testSubDataset2, labels, method = 'post')totalCorrect = correct1 + correct2# 剪枝前的准确率if len(testClassList)==0:precision_pre=0else:precision_pre = totalCorrect / len(testClassList)# 剪枝后# 预测类别为当前训练集中最多的类别predict_class_post = majorityCnt(trainClassList)if len(testClassList)==0:precision_post=0else:precision_post = testClassList.count(predict_class_post)/len(testClassList) # 使用训练集中最多的类别预测剪枝后的测试集的准确度print(precision_post)# 如果剪枝后的精确度比剪枝前更高,则进行剪枝,# 返回剪枝后的预测类别predict_class_post与剪枝后预测对的个数correct_post;# 否则返回剪枝前的树myTree以及剪枝前预测正确的个数totalCorrectprint("precision_post",precision_post)print("precision",precision_pre)if precision_post > precision_pre:correct_post = testClassList.count(predict_class_pre)return predict_class_pre, correct_postelse:myTree[bestFeature]["<="+str(round(bestSplitValue,2))] = leftTreemyTree[bestFeature][">"+str(round(bestSplitValue,2))] = rightTreereturn myTree, totalCorrectelse :myTree[bestFeature]["<="+str(round(bestSplitValue,2))] = createTree(trainSubDataset1,testSubDataset1, labels, method = None)myTree[bestFeature][">"+str(round(bestSplitValue,2))] = createTree(trainSubDataset2,testSubDataset2, labels, method = None)predict_class_pre = majorityCnt(trainClassList)# 使用训练集中最多的类别预测当前未划分的测试集的准确度precision_pre = testClassList.count(predict_class_pre)/len(testClassList)print("precision",precision_pre)return myTreeif __name__=='__main__':trainDataset, testDataset, labels = readDataset()print(labels)labelsForPost = copy.deepcopy(labels)values = createTree(trainDataset, testDataset, labels, method = "post")print(values)if len(values) == 1:myTree = values elif len(values) == 2:myTree = values[0]createPlot(myTree, method = "post")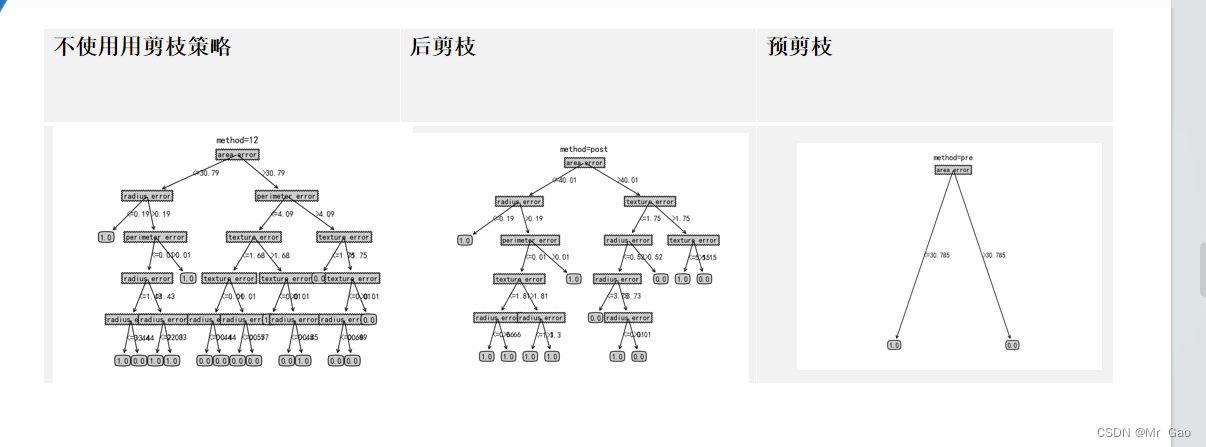
3.KNN+PCA可视化
import numpy as np
from sklearn.datasets import load_iris
from sklearn.model_selection import train_test_split
from sklearn.neighbors import KNeighborsClassifier
from sklearn.metrics import accuracy_score
from sklearn.decomposition import PCA # PCA主成分分析类
import matplotlib.pyplot as plt # 画图工具
import pandas as pd# 加载鸢尾花数据集
iris = load_iris()
X = iris.data # 特征向量
y = iris.target # 类别标签
#df = pd.DataFrame(iris.data, columns=iris.feature_names)
#df.to_csv(r'D:\coursework\maching_learning\iris.csv', index=None)# 划分训练集和测试集
X_train, X_test, y_train, y_test = train_test_split(X, y, test_size=0.4, random_state=42) #训练集占比为0.4# 构建KNN分类器
knn = KNeighborsClassifier(n_neighbors=10) # 设置邻居数量为10
knn.fit(X_train, y_train) # 在训练集上训练模型# 在测试集上进行预测
y_pred = knn.predict(X_test)# 计算分类准确率
accuracy = accuracy_score(y_test, y_pred)
print("测试集准确率为: {:.2%}".format(accuracy))iris = load_iris()
y = iris.target
X = iris.data
#X.shape
#调用PCA
pca = PCA(n_components=2) # 降到2维
pca = pca.fit(X) #拟合模型
X_dr = pca.transform(X) #获取新矩阵 (降维后的)
#X_dr#也可以fit_transform一步到位
#X_dr = PCA(2).fit_transform(X)
plt.figure()
plt.scatter(X_dr[y==0, 0], X_dr[y==0, 1], c="red", label=iris.target_names[0])
plt.scatter(X_dr[y==1, 0], X_dr[y==1, 1], c="black", label=iris.target_names[1])
plt.scatter(X_dr[y==2, 0], X_dr[y==2, 1], c="orange", label=iris.target_names[2])
plt.legend()
plt.title('PCA of IRIS dataset')y_train_pca=pca.transform(X_test) #获取新矩阵 (降维后的)plt.figure()
plt.scatter(y_train_pca[y_pred==0, 0], y_train_pca[y_pred==0, 1], c="red", label=iris.target_names[0])
plt.scatter(y_train_pca[y_pred==1, 0], y_train_pca[y_pred==1, 1], c="black", label=iris.target_names[1])
plt.scatter(y_train_pca[y_pred==2, 0], y_train_pca[y_pred==2, 1], c="orange", label=iris.target_names[2])
plt.legend()
plt.title('predict of IRIS test_dataset')
plt.show()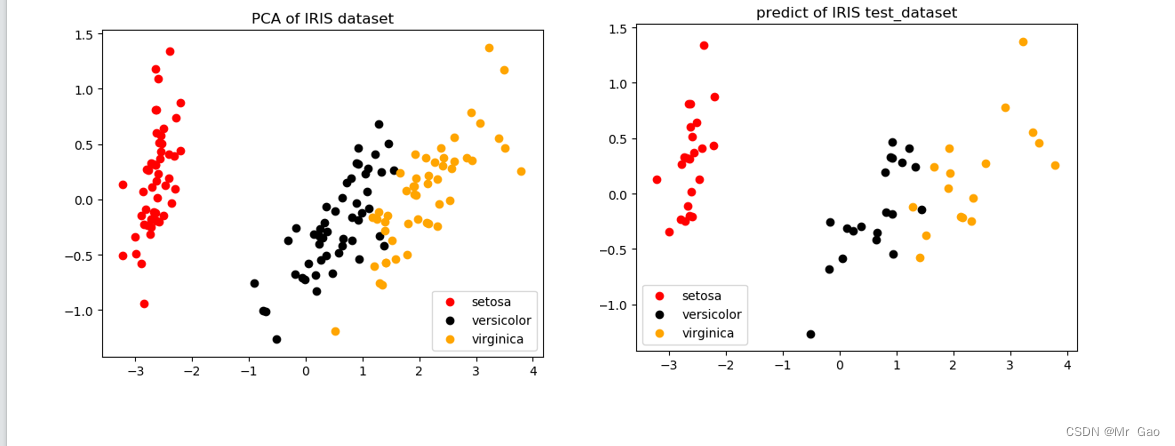
KD树算法:
import math
import numpy as np
from sklearn.datasets import load_iris
from sklearn.model_selection import train_test_split
from sklearn.neighbors import KNeighborsClassifier
from sklearn.metrics import accuracy_score
from sklearn.decomposition import PCA # PCA主成分分析类
import matplotlib.pyplot as plt # 画图工具
import pandas as pd
import time# 加载鸢尾花数据集
iris = load_iris()
X = iris.data # 特征向量pts = X #点集,任意维度的点集class Node():def __init__(self,pt,leftBranch,rightBranch,dimension):self.pt = ptself.leftBranch = leftBranchself.rightBranch = rightBranchself.dimension = dimensionclass KDTree():def __init__(self,data):self.nearestPt = Noneself.nearestDis = math.infdef createKDTree(self,currPts,dimension):if(len(currPts) == 0):return Nonemid = self.calMedium(currPts)sortedData = sorted(currPts,key=lambda x:x[dimension])leftBranch = self.createKDTree(sortedData[:mid],self.calDimension(dimension))rightBranch = self.createKDTree(sortedData[mid+1:],self.calDimension(dimension))return Node(sortedData[mid],leftBranch,rightBranch,dimension)def calMedium(self,currPts):return len(currPts) // 2def calDimension(self,dimension): # 区别就在于这里,几维就取余几return (dimension+1)%len(targetPt)def calDistance(self,p0,p1):return math.sqrt((p0[0]-p1[0])**2+(p0[1]-p1[1])**2)def getNearestPt(self,root,targetPt):self.search(root,targetPt)return self.nearestPt,self.nearestDisdef search(self,node,targetPt):if node == None:returndist = node.pt[node.dimension] - targetPt[node.dimension]if(dist > 0):#目标点在节点的左侧或上侧self.search(node.leftBranch,targetPt)else:self.search(node.rightBranch,targetPt)tempDis = self.calDistance(node.pt,targetPt)if(tempDis < self.nearestDis):self.nearestDis = tempDisself.nearestPt = node.pt#回溯if(self.nearestDis > abs(dist)):if(dist > 0):self.search(node.rightBranch,targetPt)else:self.search(node.leftBranch,targetPt)def get_min_distance(X,targetPt):small=math.sqrt(sum((X[0]-targetPt)**2))re_i=0index=0for point in X[1:]:d=math.sqrt(sum((point-targetPt)**2))if d<small:small=dre_i=indexindex=index+1return re_iif __name__ == "__main__":targetPt = X[0] #目标点,任意维度的点kdtree = KDTree(pts) root = kdtree.createKDTree(pts,0) # 记录开始时间start_time = time.time()for point in X:re_i = get_min_distance(X,point)# 记录结束时间end_time = time.time()# 计算并打印执行时间elapsed_time = end_time - start_timeprint(f"传统遍历方法执行时间: {elapsed_time}秒")# 记录开始时间start_time = time.time()for point in X:pt,minDis = kdtree.getNearestPt(root,point)# 记录结束时间end_time = time.time()# 计算并打印执行时间elapsed_time = end_time - start_timeprint(f"kd树执行时间: {elapsed_time}秒")运行结果:
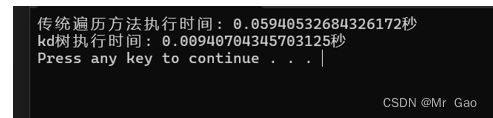
对了,这一次实验,其实对于KNN还少了几个实验,一个是k值得超参数实验,一个是KNN基于不同距离计算公示的考察。