算法练习第19天|222.完全二叉树的节点个数

222.完全二叉树的节点个数

222. 完全二叉树的节点个数 - 力扣（LeetCode）https://leetcode.cn/problems/count-complete-tree-nodes/description/

题目描述：

给你一棵 完全二叉树 的根节点 root ，求出该树的节点个数。题目数据保证输入的树是 完全二叉树

完全二叉树的定义如下：在完全二叉树中，除了最底层节点可能没填满外，其余每层节点数都达到最大值，并且最下面一层的节点都集中在该层最左边的若干位置。若最底层为第 h 层，则该层包含 1~ 2h 个节点。

示例 1：

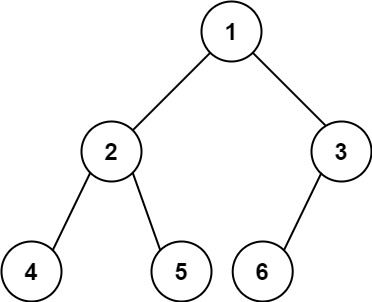
输入：root = [1,2,3,4,5,6]
输出：6

示例 2：

输入：root = []
输出：0

示例 3：

输入：root = [1]
输出：1

题目分析：

按照前文所讲的二叉树的递归遍历以及层序遍历，可以将完全二叉树看作普通二叉树处理，进行节点个数的统计。思路较为简单，代码如下：

后序递归遍历解法：

/*** Definition for a binary tree node.* struct TreeNode {*     int val;*     TreeNode *left;*     TreeNode *right;*     TreeNode() : val(0), left(nullptr), right(nullptr) {}*     TreeNode(int x) : val(x), left(nullptr), right(nullptr) {}*     TreeNode(int x, TreeNode *left, TreeNode *right) : val(x), left(left), right(right) {}* };*/
class Solution {
public://后序递归,第一步，确定函数参数以及返回值int countNodes(TreeNode* root) {      //递归第二步,确定递归终止条件。当递归函数指针root为空，递归终止if(root == nullptr) return 0;//递归第三步，确定单层递归逻辑：统计左右子树的节点个数，然后相加再加1int left = countNodes(root->left);  //左int right = countNodes(root->right);  //右int result = 1 + left + right;   //1就是后序遍历顺序的中           return result;}
};

层序遍历解法（也叫迭代法）：

class Solution {
public://层序遍历int countNodes(TreeNode* root) {      if(root == nullptr) return 0;queue<TreeNode*> que;que.push(root);int result = 0;while(!que.empty()) {int size = que.size();for(int i = 0; i < size; i++){TreeNode * node = que.front();que.pop();result++;if(node->left)  que.push(node->left);if(node->right)  que.push(node->right);}}return result;}
};

完全二叉树解法：

但是上述方法都是将完全二叉树当做普通二叉树来进行题目的求解，这样就忽略了完全二叉树的性质。完全二叉树时除了最底层的节点可能不满之外，其余层均是满的，并且，最底层的节点必须是严格从左往右依次排列的，不能有跳跃（如下面的最右侧的二叉树，蓝色框内存在跳跃，所以其不是完全二叉树）。

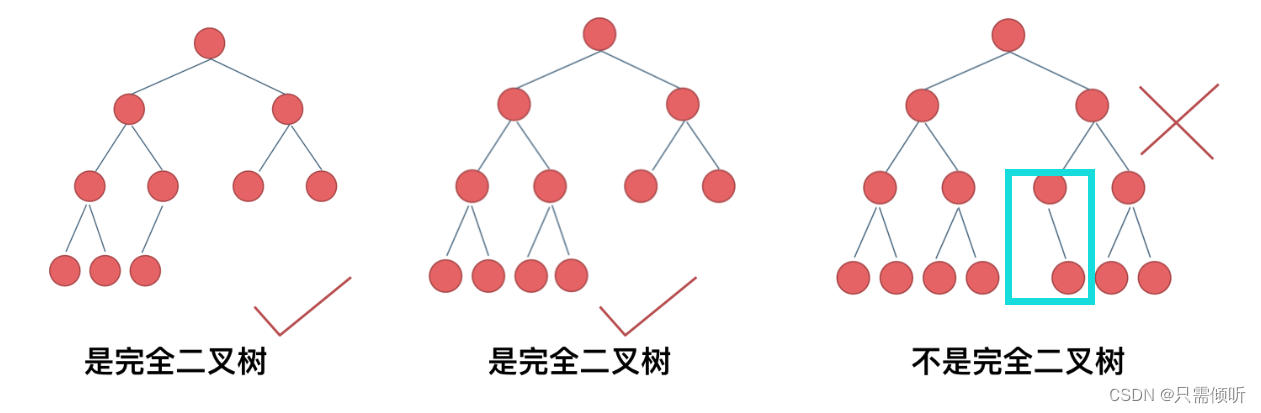
如果完全二叉树最底层也填满了的话，这时它就也是满二叉树。节点个数为 $2^{n} -1$ ，n为二叉树的层数。

所以完全二叉树只有两种情况，情况一：就是满二叉树，情况二：最后一层叶子节点没有满。

对于情况一，可以直接用 $2^{n} -1$ 来计算。

对于情况二，分别递归左孩子，和右孩子，递归到某一深度一定会有左孩子或者右孩子为满二叉树，然后依然可以按照情况1来计算。

关键点来了，怎么判断左右孩子是不是满二叉树？在完全二叉树中，如果递归一直向左遍历的深度等于递归一直向右遍历的深度，那说明就是满二叉树。前提是一定要在完全二叉树中。

所以，该解法的递归终止条件如下所示：

if (root == nullptr) return 0; 
// 开始根据左深度和右深度是否相同来判断该子树是不是满二叉树
TreeNode* left = root->left;
TreeNode* right = root->right;
int leftDepth = 0, rightDepth = 0; // 这里初始为0是有目的的，为了下面求指数方便
while (left) {  // 求左子树深度left = left->left;leftDepth++;
}
while (right) { // 求右子树深度right = right->right;rightDepth++;
}
if (leftDepth == rightDepth) {return (2 << leftDepth) - 1; // 注意(2<<1) 相当于2^2，返回满足满二叉树的子树节点数量
}

递归三部曲，第三部，单层递归的逻辑：（可以看出使用后序遍历）

int leftTreeNum = countNodes(root->left);       // 左
int rightTreeNum = countNodes(root->right);     // 右
int result = leftTreeNum + rightTreeNum + 1;    // 中
return result;

整体代码如下：

class Solution {
public://递归第一步int countNodes(TreeNode* root) { //递归第二步，确定递归终止条件     if(root == nullptr) return 0;TreeNode *left = root->left;TreeNode *right = root->right;int leftDepth=0 , rightDepth = 0;while(left)  //一直向左遍历，求深度{leftDepth++;left = left->left;}while(right) //一直向右遍历，求深度{rightDepth++;right = right->right;}if(leftDepth == rightDepth)  //当前的完全二叉树为满二叉树return (2 << leftDepth) - 1;  //2的n次方减一//递归第三步，确认单层递归逻辑//不然的话，就递归统计左右子树的节点数。每一级递归都会进行上面的满二叉树判断int left = countNodes(root->left);  //左int right = countNodes(root->right);  //右int result = left + right + 1;  //中return result;}
};

该解法与后续递归解法的不同之处就在于递归终止条件，该解法核心思想致力于逐子树判断是否为满二叉树。如果是，使用 $2^{n} -1$ 计算节点数；如果不是，则进行下一层的递归countNodes。思路很巧妙。