【数据结构】树与二叉树遍历算法的应用（求叶子节点个数、求树高、复制二叉树、创建二叉树、二叉树存放表达式、交换二叉树每个结点的左右孩子）

news/2025/2/22 23:02:13/

目录

  • 求叶子节点个数、求树高、复制二叉树、创建二叉树、二叉树存放表达式、交换二叉树每个结点的左右孩子
    • 应用一：统计二叉树中叶子结点个数的算法
      • 写法一：使用静态变量
      • 写法二：传入 count 作为参数
      • 写法三：不使用额外变量
    • 应用二：二叉树存放表达式
    • 应用三：求二叉树的高
    • 应用四：复制二叉树
    • 应用五：二叉树的建立
    • 应用六：交换二叉树每个结点的左右孩子
      • Swap 函数（先序遍历）：
      • Swap 函数（中序遍历）××× 不可行：
      • Swap 函数（后序遍历）：
  • 求叶子节点个数、求树高、复制二叉树、创建二叉树完整代码示例

求叶子节点个数、求树高、复制二叉树、创建二叉树、二叉树存放表达式、交换二叉树每个结点的左右孩子

  1. 遍历二叉树的应用都是基于递归法实现的，递归的知识点以及例题可以参考文章: 【数据结构与算法】递推法和递归法解题（递归递推算法典型例题）
  2. 树与二叉树知识点可参考：【数据结构】树与二叉树（递归法先序、中序、后序、层次遍历二叉树、二叉树的建立以及求树高的方法）

注：本文二叉树的结构体定义为（采用二叉链表的定义）：
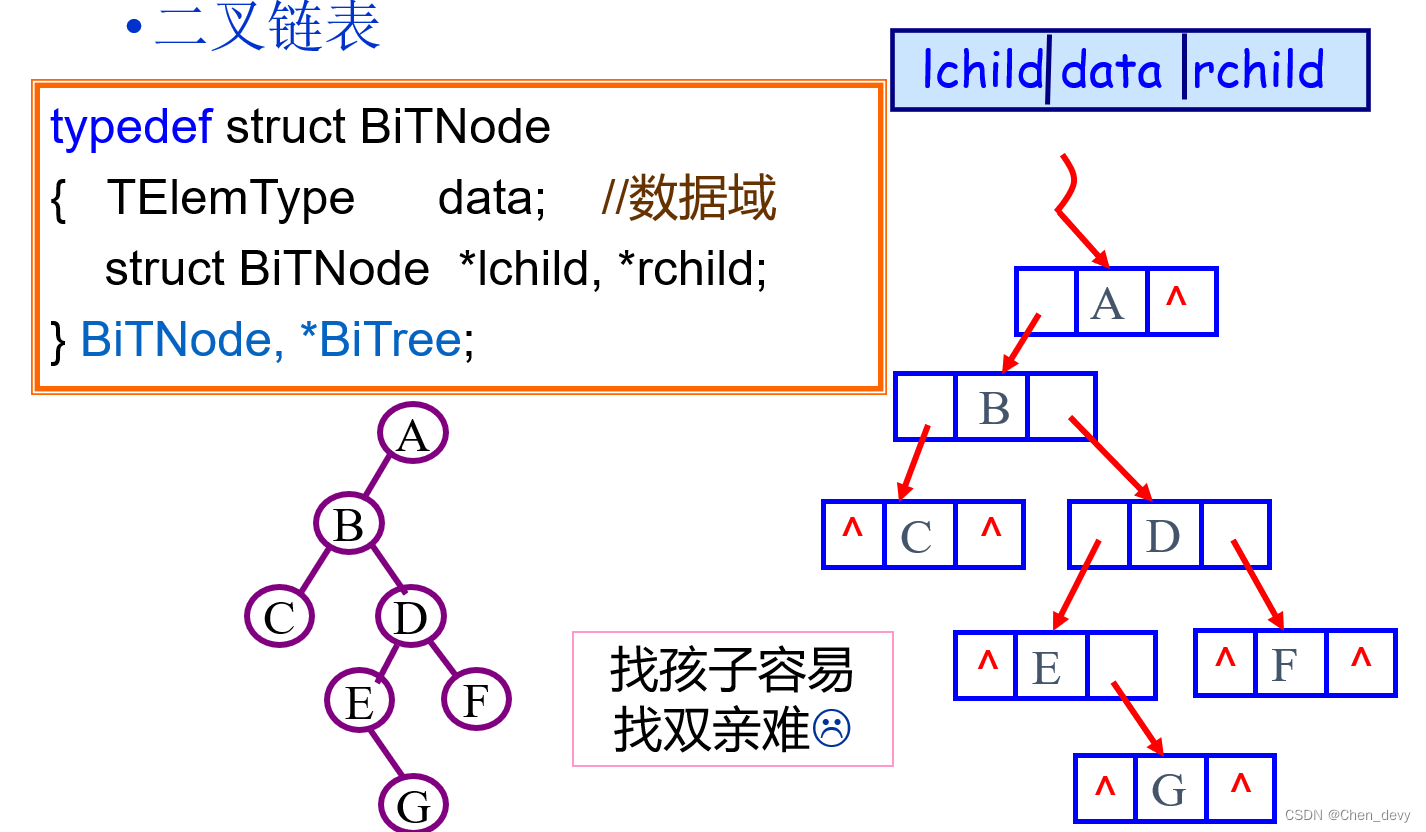
在这里插入图片描述

//采用二叉链表的定义
typedef struct TreeNode{int data;//数据域TreeNode *rchild;//右孩子指针TreeNode *lchild;//左孩子指针
}TreeNode, *BiTree;
//注意结构体名称别写错！！！

应用一：统计二叉树中叶子结点个数的算法

写法一：使用静态变量

  • 函数使用了一个静态局部变量 count 来统计叶子节点的数量。
  • 每次调用函数时，count 的值都会保持，并且在遇到叶子节点时自增。
int LeafCount(BiTree T){static int count=0; // 静态局部变量，保持在函数调用之间的值if(T){if((T->lchild==NULL)&&(T->rchild==NULL)){count++; // 每当遇到叶子节点，count自增}else{LeafCount(T->lchild);LeafCount(T->rchild);}}return count; // 返回叶子节点数
}

写法二：传入 count 作为参数

  • 函数将 count 作为参数传递，并通过引用进行修改。
int LeafCount(BiTree T, int &count) {if (T) {if (T->lchild == NULL && T->rchild == NULL)count++;else {LeafCount(T->lchild, count);LeafCount(T->rchild, count);}}return count;
}

写法三：不使用额外变量

  • 函数直接通过递归计算叶子节点的数量，不使用额外的变量。
  • 当遇到空树，返回 0；当遇到叶子节点，返回 1；否则，递归计算左右子树的叶子节点数，并返回它们的和。
int LeafCount3(BiTree T){  if (!T) return 0;	// 空树叶子结点个数为0if (!T->lchild && !T->rchild) return 1; // 找到一个叶节点return LeafCount3(T->lchild) + LeafCount3(T->rchild);	// 否则为左右叶子结点个数之和
}

应用二：二叉树存放表达式

二叉树存放表达式 ：

波兰式： +*dj/e+hi
中缀表示: d*j+e/(h+i)
逆波兰式: dj*ehi+/+

在这里插入图片描述

应用三：求二叉树的高

求二叉树深度算法(后序遍历）
m a x { 左子树深度 + 1 ，右子树深度 + 1 } max\{左子树深度+1，右子树深度+1\} max{左子树深度+1，右子树深度+1}

算法实现原理：

  1. 函数 Get_Height 接收一个指向树节点的指针 node 作为参数，表示要计算高度的二叉树的根节点。

  2. 首先，检查传入的节点是否为空。如果是空节点（即 node == NULL），那么树的高度为 0，因此函数直接返回 0。

  3. 如果节点不为空，则进入递归过程。它通过分别递归调用 Get_Height 函数来计算左子树和右子树的高度。

  4. 递归的终止条件就是当遇到叶子节点时，即左子节点和右子节点都为 NULL，这时高度为 0。

  5. 在每一层递归中，通过比较左子树的高度和右子树的高度，选择其中较大的一个，然后加上根节点，就得到了以当前节点为根的子树的高度。

  6. 最终，根据左右子树的高度计算出的最大高度加上根节点，就是整棵树的高度。

  7. 然后，返回return Tree_Height这个树的高度。

//求二叉树的高
int Get_Height(TreeNode* node) {if (node == NULL) return 0;//终止条件：如果为空节点，返回0，表示高度为0int Left_Height = Get_Height(node->lchild);//递归求左子树高度int Right_Hegiht = Get_Height(node->rchild);//递归求右子树高度int Tree_Height = 1 + (Left_Height > Right_Height?Left_Height:Right_Height);//计算树高return Tree_Height;
}

应用四：复制二叉树

复制二叉树采用后序遍历的方法来实现的，具体实现原理如下：

  1. 结点生成（GetTreeNode函数）：

    • GetTreeNode函数用于创建一个二叉树的结点。
    • 它接收三个参数：
      • item：表示结点的数据值。
      • lptr：表示左子树的指针。
      • rptr：表示右子树的指针。
    • 在函数内部，它首先分配一个新的结点（Q）的内存空间。
    • 然后，将传入的数据值、左子树指针和右子树指针分别赋值给新结点的对应字段。
    • 最后，返回新创建的结点。

  2. 后序遍历（CopyTree函数）：

    • CopyTree函数用于复制一个二叉树。
    • 如果需要复制的二叉树的结点为空，直接返回NULL。
    • 否则，递归地复制左子树和右子树：
      • 如果左子树非空，调用CopyTree函数复制左子树。
      • 如果右子树非空，调用CopyTree函数复制右子树。
    • 创建一个新的结点，将原结点的数据值、复制的左子树和复制的右子树分别赋值给新结点的对应字段。
    • 返回复制后的新二叉树。

代码示例：

// 生成一个二叉树的结点
TreeNode* GetTreeNode(int item, TreeNode *lptr , TreeNode *rptr ){BiTree Q;if ( !(Q = (TreeNode*)malloc(sizeof(TreeNode))) ) {exit(1);}Q-> data = item;Q-> lchild = lptr;    Q-> rchild = rptr;return Q;
}//后序遍历 
TreeNode *CopyTree(TreeNode *T) {  //如果需要复制的二叉树的结点为空 就直接退出 BiTree newlptr=NULL;BiTree newrptr=NULL;BiTree newT=NULL;if (!T)    return NULL;if (T->lchild ) newlptr = CopyTree(T->lchild);//复制左子树if (T->rchild ) newrptr = CopyTree(T->rchild);//复制右子树newT = GetTreeNode(T->data, newlptr, newrptr);return newT;
} // CopyTree

注意：在给定的代码中，CopyTree 函数用于复制一个二叉树。它会递归地复制二叉树的每个节点，并且生成一个新的二叉树。在这个过程中，新的二叉树和原始二叉树的节点是独立的，它们的内存地址不同。这是因为 CopyTree 函数中调用 GetTreeNode 函数，该函数每次都会动态分配内存以创建新的节点。

所以，复制后的二叉树和原始二叉树之间的节点地址没有任何关系，它们是相互独立的。修改复制后的二叉树的节点不会影响原始二叉树。

应用五：二叉树的建立

以先序序列定义一棵二叉树：输入所要建立的二叉树的先序序列，建立二叉链表。
在输入的二叉树的先序序列中，加入空树明确表示"#"。

在这里插入图片描述

按先序遍历序列建立二叉树的二叉链表
已知先序 序列为：ABC##DE##F###

二叉树的建立的算法：

typedef struct TreeNode{int data;//数据域TreeNode *rchild;//右孩子指针TreeNode *lchild;//左孩子指针
}TreeNode, *BiTree;//二叉树的建立的算法(按先序遍历序列建立)
void CreateBiTree(BiTree &T) {char ch; scanf("%c",&ch);if (ch=='#') T = NULL;else {T = (TreeNode *)malloc(sizeof(TreeNode))； T->data = ch;      // 生成根结点CreateBiTree(T->lchild); // 构造左子树CreateBiTree(T->rchild); // 构造右子树}
}

应用六：交换二叉树每个结点的左右孩子

以上代码实现了交换二叉树每个节点的左右孩子的功能，分别使用了先序、中序和后序遍历的方式。

遍历二叉树算法的变式：

  1. Swap 函数（先序遍历）：

    • 从根节点开始，先交换当前节点的左右孩子。
    • 然后递归地对左子树和右子树执行相同的操作。

  2. Swap2 函数（中序遍历）：

    • 与先序遍历不同，中序遍历中需要先对左子树进行操作，然后交换当前节点的左右孩子，最后对右子树进行操作。
    • 但是这个实现方式是错误的，因为在交换左子树之后，对右子树进行操作时，右子树的结构已经发生了变化，导致结果错误。

  3. Swap3 函数（后序遍历）：

    • 与先序遍历类似，但是是在遍历完左右子树之后再交换当前节点的左右孩子。
    • 这样可以保证在交换左右孩子时，左右子树的结构不会被改变。

通过上述分析，正确的交换方式是采用先序或后序遍历，中序遍历方式不适合这个场景。

Swap 函数（先序遍历）：

//前序
void Swap(BiTree& T){//（先序遍历） if(T){//根节点 if(T->lchild||T->rchild){BiTree p;p= T->lchild;T->lchild = T->rchild;T->rchild = p;}Swap(T->lchild);Swap(T->rchild);}
}

Swap 函数（中序遍历）××× 不可行：

//中序的不行 
void Swap2(BiTree& T){//（中序遍历） if(T){//根节点 Swap2(T->lchild);if(T->lchild||T->rchild){BiTree p;p= T->lchild;T->lchild = T->rchild;T->rchild = p;}Swap2(T->rchild);}
}

Swap 函数（后序遍历）：

//后序
void Swap3(BiTree& T){//（后序遍历） if(T){//根节点 Swap3(T->lchild);Swap3(T->rchild);if(T->lchild||T->rchild){BiTree p;p= T->lchild;T->lchild = T->rchild;T->rchild = p;}}}

求叶子节点个数、求树高、复制二叉树、创建二叉树完整代码示例

输入示例：ABC##DE##F###

#include<iostream>
using namespace std;typedef struct TreeNode{int data;//数据域TreeNode *rchild;//右孩子指针TreeNode *lchild;//左孩子指针
}TreeNode, *BiTree;//二叉树的建立的算法(按先序遍历序列建立)
void CreateBiTree(BiTree &T) {char ch; scanf("%c",&ch);if (ch=='#') T = NULL;else {T = (TreeNode*)malloc(sizeof(TreeNode));T->data = ch;      // 生成根结点CreateBiTree(T->lchild); // 构造左子树CreateBiTree(T->rchild); // 构造右子树}
}//求叶子结点 
int LeafCount(BiTree T){static int count=0;//或者定义成全局变量 /*这里使用局部静态变量*/if(T){if((T->lchild==NULL)&&(T->rchild==NULL)){//判断T是否为叶子结点count++;//每次递归调用//当T为叶子时，count自加}else{//递归：求T左、右子树上的叶子结点数LeafCount(T->lchild);LeafCount(T->rchild);}}return count;
}//求叶子节点的写法三 
int LeafCount3(BiTree T){  if (!T) return 0;	//空树叶子结点个数为0if (!T->lchild && !T->rchild) return 1; //若根节点没有左右孩子叶子结点个数为1return LeafCount3(T->lchild) + LeafCount3(T->rchild);	//否则为左右叶子结点个数之和
}//求树高 
int Get_Height(BiTree node){//递归 求树高 if(node==NULL) return 0;else{int Left_Height = Get_Height(node->lchild);int Right_Height = Get_Height(node->rchild);int Tree_Height = 1 + (Left_Height > Right_Height?Left_Height:Right_Height);//计算树高return Tree_Height;}}
//先序遍历 
void xxbl(BiTree T){if(T){//递归调用的结束条件printf("%c",T->data);//访问结点xxbl(T->lchild);//遍历左子树xxbl(T->rchild);//遍历右子树}}
//中序遍历 
void zxbl(BiTree T){if (T) {zxbl(T->lchild); printf("%c",T->data); zxbl(T->rchild);}
}
//后序遍历 
void hxbl(BiTree T){if(T){hxbl(T->lchild); hxbl(T->rchild); printf("%c",T->data);}
}// 
// 生成一个二叉树的结点
TreeNode* GetTreeNode(int item, TreeNode *lptr , TreeNode *rptr ){BiTree Q;if ( !(Q = (TreeNode*)malloc(sizeof(TreeNode))) ) {exit(1);}Q-> data = item;Q-> lchild = lptr;    Q-> rchild = rptr;return Q;
}//后序遍历 
TreeNode *CopyTree(TreeNode *T) {  //如果需要复制的二叉树的结点为空 就直接退出 BiTree newlptr=NULL;BiTree newrptr=NULL;BiTree newT=NULL;if (!T)    return NULL;if (T->lchild ) { newlptr = CopyTree(T->lchild);//复制左子树} if (T->rchild ){ newrptr = CopyTree(T->rchild);//复制右子树} newT = GetTreeNode(T->data, newlptr, newrptr);return newT;
} // CopyTreeint main(){BiTree T;//例如输入：ABC##DE##F### 来创建二叉树 CreateBiTree(T);cout<<"先序："; xxbl(T);cout<<endl;cout<<"中序："; zxbl(T);cout<<endl;cout<<"后序："; hxbl(T);cout<<endl;cout<<"树高为：" ;cout<<Get_Height(T)<<endl;cout<<"叶子节点的个数为：";cout<<LeafCount3(T)<<endl; //复制二叉树BiTree Q;Q=CopyTree(T); cout<<"复制后的二叉树 以先序输出："; xxbl(Q);cout<<endl;//修改一下Q 左子树根节点的数据 观察原本T 是否改变 Q->lchild->data='Z';cout<<"修改的二叉树 Q以先序输出："; xxbl(Q);cout<<endl;cout<<"T先序："; xxbl(T);cout<<endl;return 0; 
}

感谢您的阅读！

  1. 遍历二叉树的应用都是基于递归法实现的，递归的知识点以及例题可以参考文章: 【数据结构与算法】递推法和递归法解题（递归递推算法典型例题）
  2. 树与二叉树知识点可参考：【数据结构】树与二叉树（递归法先序、中序、后序、层次遍历二叉树、二叉树的建立以及求树高的方法）

http://www.ppmy.cn/news/1418082.html

相关文章

计算机视觉——基于深度学习检测监控视频发生异常事件的算法实现

计算机视觉——基于深度学习检测监控视频发生异常事件的算法实现

1. 简介 视频异常检测&#xff08;VAD&#xff09;是一门旨在自动化监控视频分析的技术&#xff0c;其核心目标是利用计算机视觉系统来监测监控摄像头的画面&#xff0c;并自动检测其中的异常或非常规活动。随着监控摄像头在各种场合的广泛应用&#xff0c;人工监视已经变得不…
阅读更多...
Python快速获取编程问题答案的方法库之howdoi使用详解

Python快速获取编程问题答案的方法库之howdoi使用详解

概要 howdoi是一个命令行工具，它提供了一种快速获取编程问题答案的方法，通过搜索和抓取Stack Overflow等网站的内容，直接在终端中显示编程问题的解决方案。 安装 通过pip可以轻松安装howdoi： pip install howdoi特性 快速访问编程解决方案：无需手动浏览Stack Overflow。…
阅读更多...
设计模式——迭代器模式15

设计模式——迭代器模式15

迭代器模式提供一种方法访问一个容器对象中各个元素&#xff0c;而又不需暴露该对象的内部细节。 设计模式&#xff0c;一定要敲代码理解 抽象迭代器 /*** 迭代抽象* */ public interface Iterator<A> {A next();boolean hasNext(); }迭代器实现 /*** author ggbond*…
阅读更多...
程序员副业指南

程序员副业指南

程序员副业指南 &#x1f31f; 程序员副业指南&#xff1a;如何通过技术项目和在线内容创造额外收入&#xff1f;&#x1f4d8; 正文内容&#x1f680; 个人项目开发&#x1f331; 初步探索**选择项目主题****市场调研** &#x1f6e0; 技术实现**技术栈选择**示例代码&#xf…
阅读更多...
红米手机怎么安装charles证书（Redmi K70）

红米手机怎么安装charles证书（Redmi K70）

我们到知道通过charles抓Https的包需要给手机安装charles证书才行&#xff0c;正常来说设置代理后&#xff0c;在手机系统浏览器中输入chls.pro/ssl就会下载安装证书。但是&#xff0c;在红米手机上就是下载不下来。 通过如下方法配置&#xff1a; 手机wifi网络配置代理手机浏…
阅读更多...
程设练习一 心得

程设练习一 心得

小蒟蒻程设练习一心得~ 文章目录 debug1542 数列题干心得 1549 2的幂次 I题干心得 1583 彩球题干心得 1484 刷油漆题干思路&#xff08;谢大&#xff09;心得 1539 区间题干心得 1576 分段题干心得 1560 平方数题干思路&#xff08;谢大&#xff09;心得 1567 3个矩形与1个正方…
阅读更多...
CMake 学习笔记2

CMake 学习笔记2

其他很好的总结 CMake教程系列-01-最小配置示例 - 知乎 CMake 保姆级教程&#xff08;上&#xff09; | 爱编程的大丙 10-补充(完结)_哔哩哔哩_bilibili 1、基本关键字 SET命令的补充 &#xff08;1&#xff09;SET命令设置执行标准 #增加-stdc11 set(CMAKE_CXX_STANDARD…
阅读更多...
虚幻引擎启动报错记录

虚幻引擎启动报错记录

0x00007FFEF0C8917C (UnrealEditor-CoreUObject.dll)处(位于 UnrealEditor.exe 中)引发的异常: 0xC0000005: 写入位置 0x0000000000000030 时发生访问冲突。 解决办法&#xff1a;首先查看堆栈信息&#xff0c;我的项目启动是因为默认场景编译不过&#xff0c;进到编辑器配置文…
阅读更多...
最新文章

Copyright @ 2022~2023