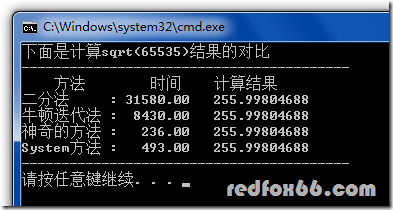
这篇博客介绍了在雷神之锤3源代码中快速求逆平方根的算法。

---

源码

雷神之锤3中的逆平方根算法如下：

float Q_rsqrt( float number ) 
{ long i; float x2, y; const float threehalfs = 1.5F ;x2 = number * 0.5F ; y = number ; i = * ( long * ) &y; // evil floating point bit level hacking i = 0x5f3759df - ( i >> 1 ); // what the fuck? y = * ( float * ) &i; y = y * ( threehalfs - ( x2 * y * y ) ); // 1st iteration 
//  y = y * ( threehalfs - ( x2 * y * y ) ); // 2nd iteration, this can be removedreturn y ;
}

函数接受一个浮点数作为输入，输出的结果是平方根的倒数。

单精度浮点数

在计算机中，单精度浮点数使用32位来储存表示：

在这32位中，最高位为符号位，后面的8位为整数ex，代表浮点数的指数，而最后的23位表示的是小数部分mx，小数部分第一位表示$2^{-1}$，第二位表示$2^{-2}$……

所以如果x是一个正浮点数，则有：

$$x=2^{e_x}(1+m_x)$$

另外，如果需要把一个浮点数转化为整数形式，则需要做如下的运算：

$$Ix=E_{X}L+M_x=L(e_x+B+m_x)$$

在上面的公式中，L指的是指数部分需要的唯一次数，这里是$2^{23}$，B是127，而M是小数部分对应的整数版本。

牛顿法

牛顿迭代法（简称牛顿法），是用于计算机求解任意连续函数的根值的一种方法。

假设对于如下的函数，我们想要求这个函数的根：

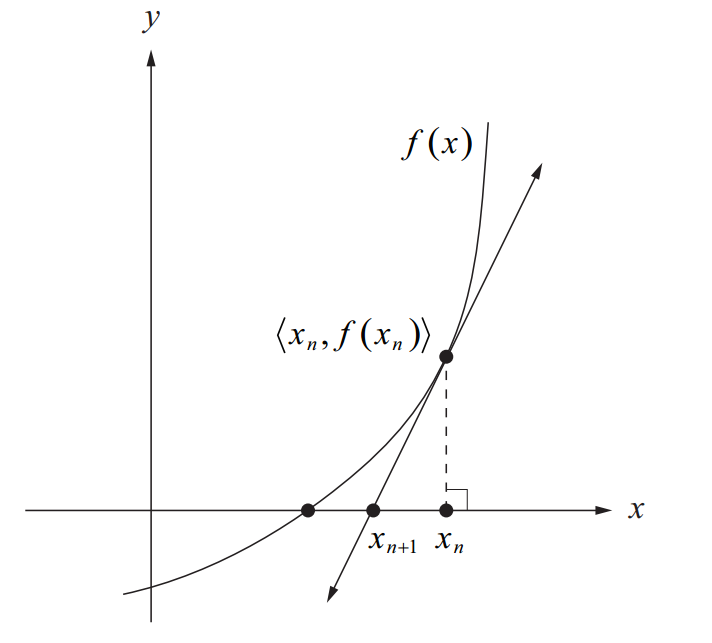
该如何求得这个根呢？首先，我们先猜一个解$x_0$，并且认为它是函数的解。

但是由于它其实并不是函数的解，那么现在，我们需要将这个解进行迭代，从而让其逼近真正的解。

在此处，我们可以在$(x_0,y_0)$处作其切线，求得该直线的方程：

$$y-f(x_0)=f^{\prime }(x_0)(x-x_0)$$

并且求直线的根，此时会发现已经对于真正的解逼近了一步。

推广到n，继续迭代，就可以足够逼近真正的解了：

$$x_{i+1}=x_i-\frac{f(x_i)}{f^{\prime }(x_i)}$$

此时发现$f(x_i)$与$f^{\prime }(x_i)$可以被一个统一的函数$g(x_i)$来表示：

$$g(x)=\frac{f(x)}{f^{\prime }(x)}$$

令ε为当前的解与真正解r的距离：
$${ϵ}_i=x_i-r$$

综合上面三个方程，可得：

$${ϵ}_{i+1}={ϵ}_i-g(x_i)$$

因此只要ε值小于某个特定的值，我们可以认为此时的x和方程的解已经很接近了。

算法分析

如果需要求得一个浮点数的平方根倒数，方程如下：

$$y=\frac{1}{\sqrt{x}}$$

转化为关于y的方程，有：

$$f(y)=\frac{1}{y^2}-x=0$$

转化为牛顿法使用的方程，有：

$$y_{n+1}=\frac{y_n(3-x{y}_n^2)}{2}$$

此时，对原本的方程等号两边同时取2的对数，就有：

$${\log }_{2}y=-\frac{1}{2}{\log }_2(1+m_x)$$

因为$m_x\ge 0$并且$m_x<1$，那么在这个区间内，可以取近似为：
$${\log }_2(1+m_x)\approx m_x+\sigma$$

根据方差的计算，当$\sigma =0.0430357$时，整体的偏差是最小的，此时上面的等号两边应该相当。

因此，把上面的完全整合起来，最终的$I_x$可以写成：
$$L{\log }_{2}x+L(B-\sigma )$$

则$$I_y\approx \frac{3}{2}L(B-\sigma )-\frac{1}{2}{I}_x$$

最终，写成代码就是：

i = 0x5f3759df - ( i >> 1 );

$$\frac{3}{2}L(B-\sigma )=0x5f3759df$$

<全文完>