前言
- 本文基础知识部分来自于b站:分享笔记的好人儿的思维导图与王道考研课程,感谢大佬的开源精神,习题来自老师划的重点以及考研真题。
- 此前我尝试了完全使用Python或是结合大语言模型对考研真题进行数据清洗与可视化分析,本人技术有限,最终数据清洗结果不够理想,相关CSDN文章便没有发出。
- 从这篇文章开始,这里我将按章节顺序,围绕考研真题展开计算机组成原理总共8章的知识,边学习边整理数据。
(考研真题待更新)
欢迎订阅专栏:408直通车
请注意,本文中的部分内容来自网络搜集和个人实践,如有任何错误,请随时向我们提出批评和指正。本文仅供学习和交流使用,不涉及任何商业目的。如果因本文内容引发版权或侵权问题,请通过私信告知我们,我们将立即予以删除。
文章目录
- 前言
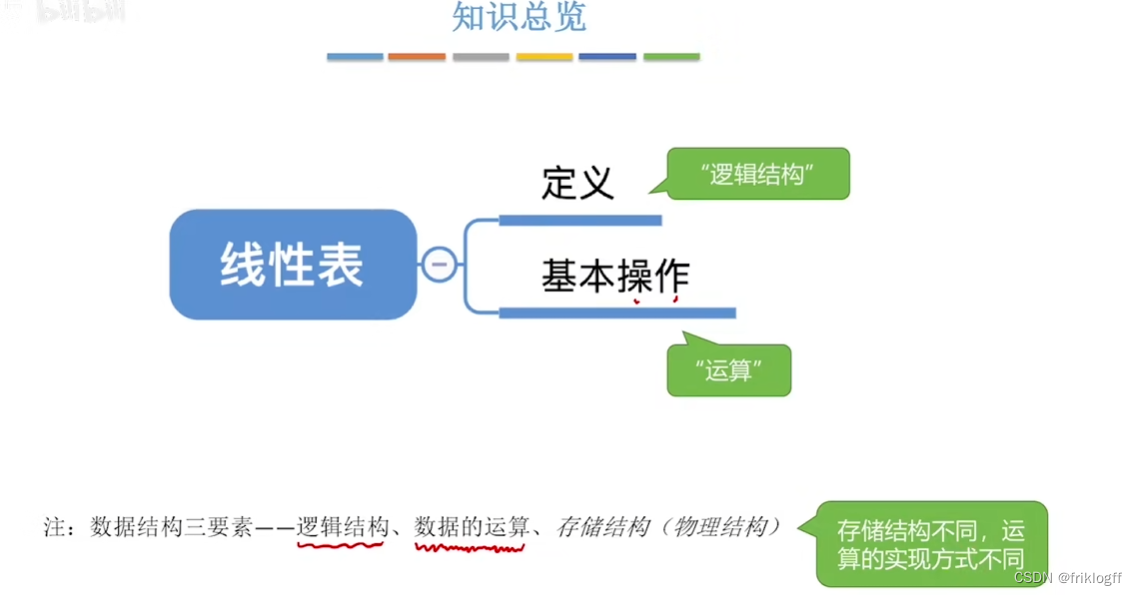
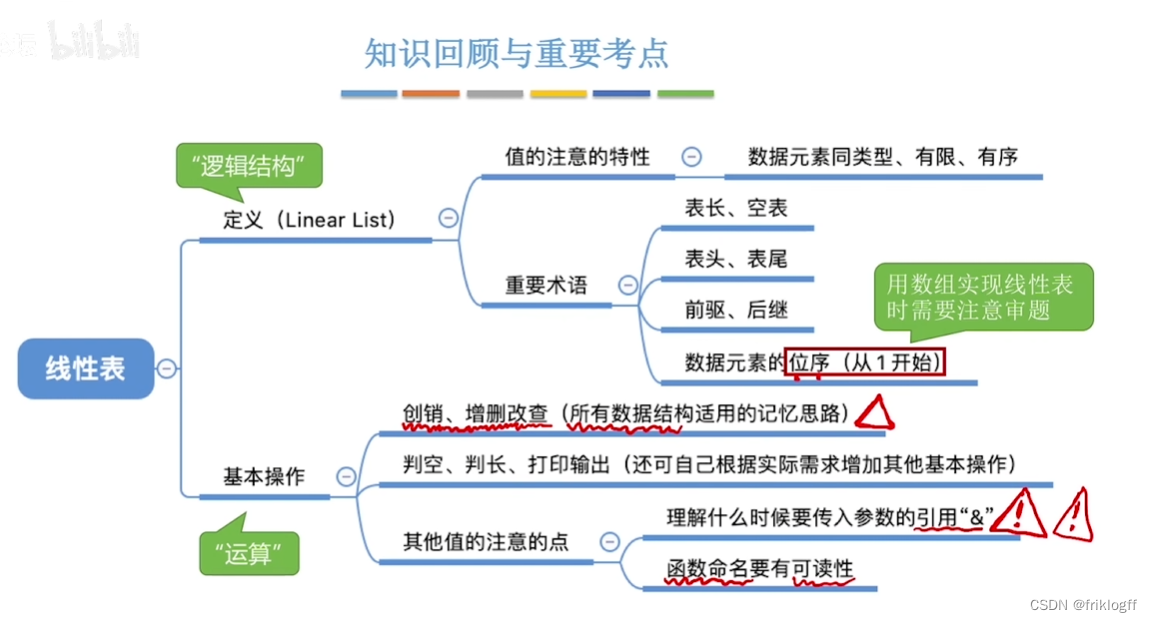
- 线性表的定义和特点
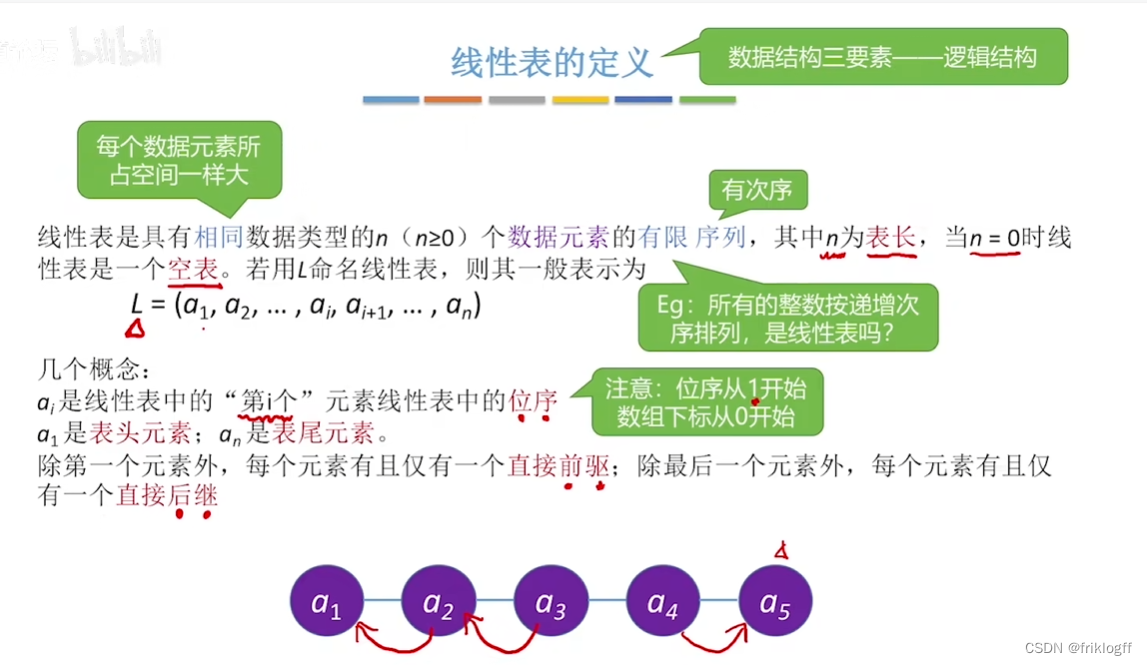
- 线性表是具有相同特性的数据元素的一个有序序列
- 特征
- 补充
- 线性表的基本操作
- 小结
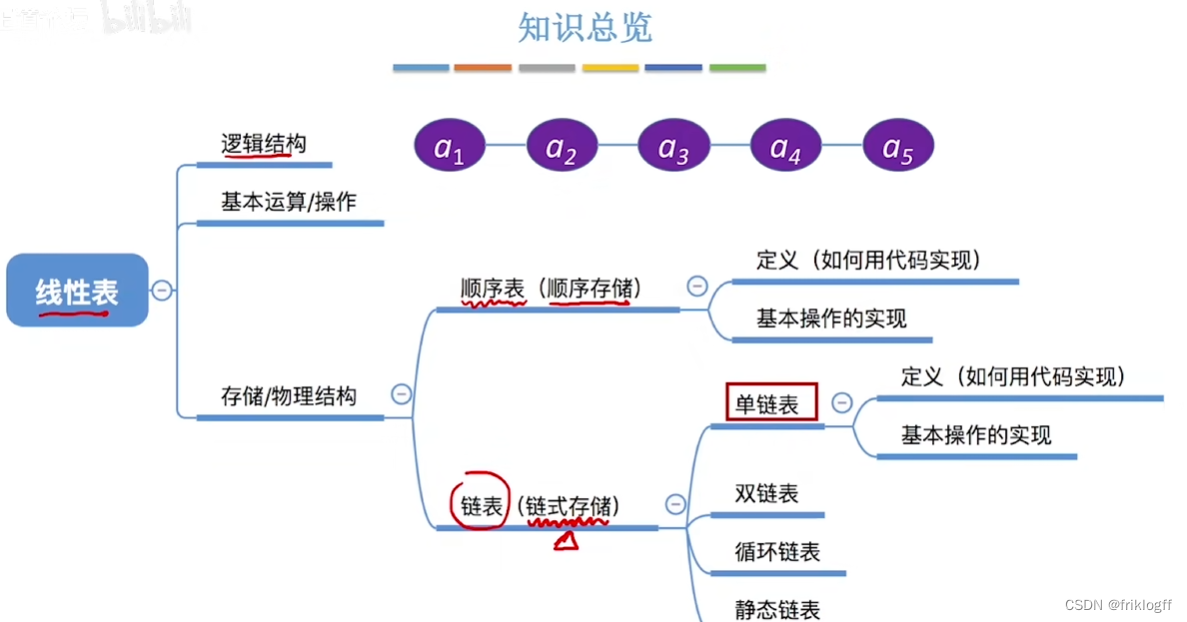
- 线性表的存储/物理结构
- 顺序表示(顺序存储结构/顺序映像)
- 顺序存储定义:把逻辑上相邻的数据元素存储在物理上相邻的存储单元中的存储结构
- 定义实现
- 特点
- 小结
- 基本操作的实现
- 顺序表的基本操作——插入
- 顺序表的基本操作——删除
- 小结
- 顺序表的基本操作——按位查找
- 顺序表的基本操作——按值查找
- 小结
- 链式表示
- 用一组物理位置任意的存储单元来存放线性表的数据元素(逻辑次序和物理次序不一定相同)
- 特点
- 结构
- 小结
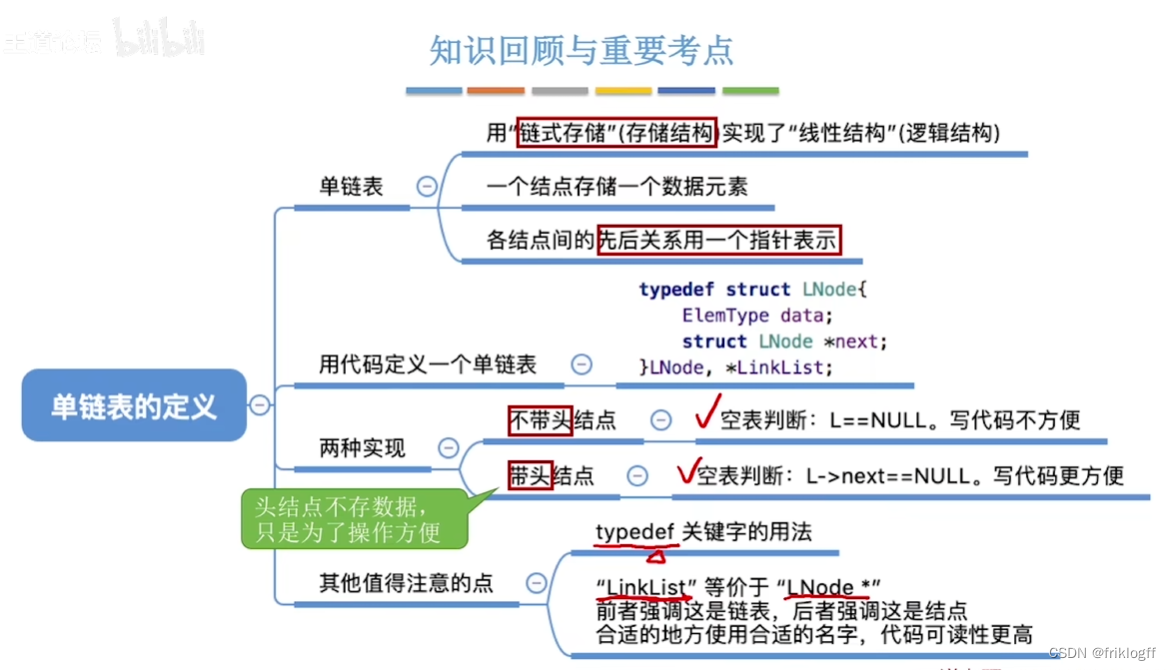
- 单链表
- 插入
- 删除
- 小结
- 查找
- 小结
- 单链表建立
- 双链表
- 小结
- 循环链表
- 小结
- 静态链表
- 小结
- 顺序表V.S.链表
- 不同链表的时间效率比较
- 顺序表和链表的比较
- 补充代码
- C++也可以用STL中的vector容器实现动态增长的数组
- 单链表(数组模拟)
- 双向链表(数组模拟)
- 考研真题
- 408 - 2023
线性表的定义和特点
线性表是具有相同特性的数据元素的一个有序序列
特征
-
元素个数有限、具有先后次序、元素类型相同
-
开始结点仅有一个直接后继,终端结点仅有一个直接前驱,内部结点仅有一个直接前驱和一个直接后继
补充
- 线性表是一种逻辑结构,表示元素一对一的相邻关系,顺序表和链表是存储结构
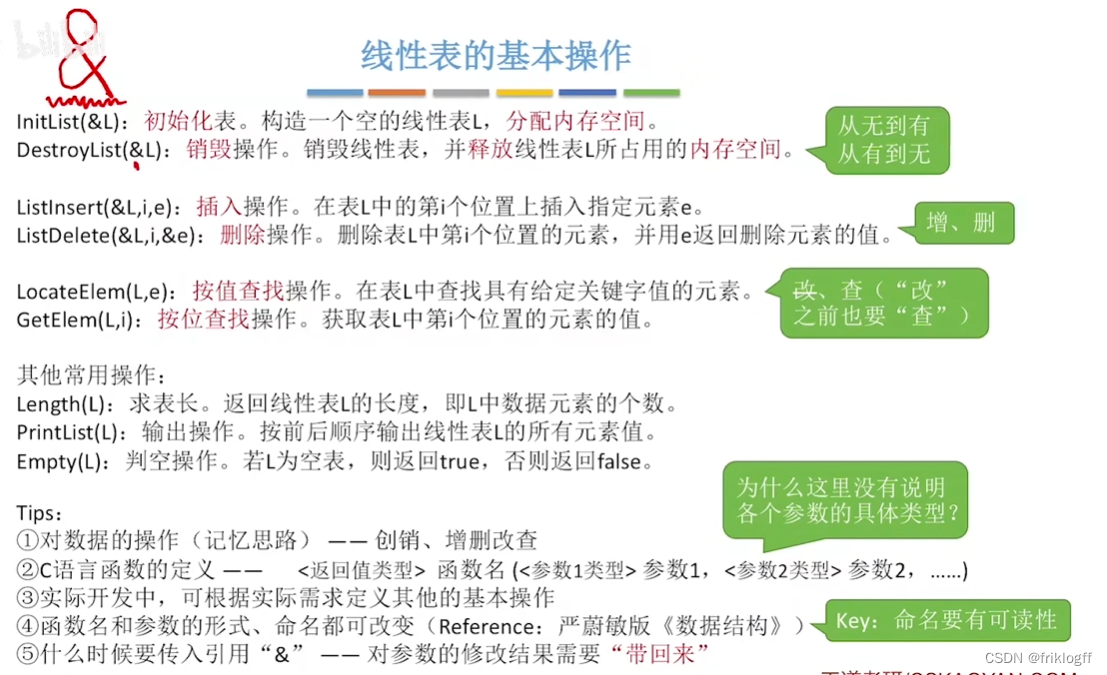
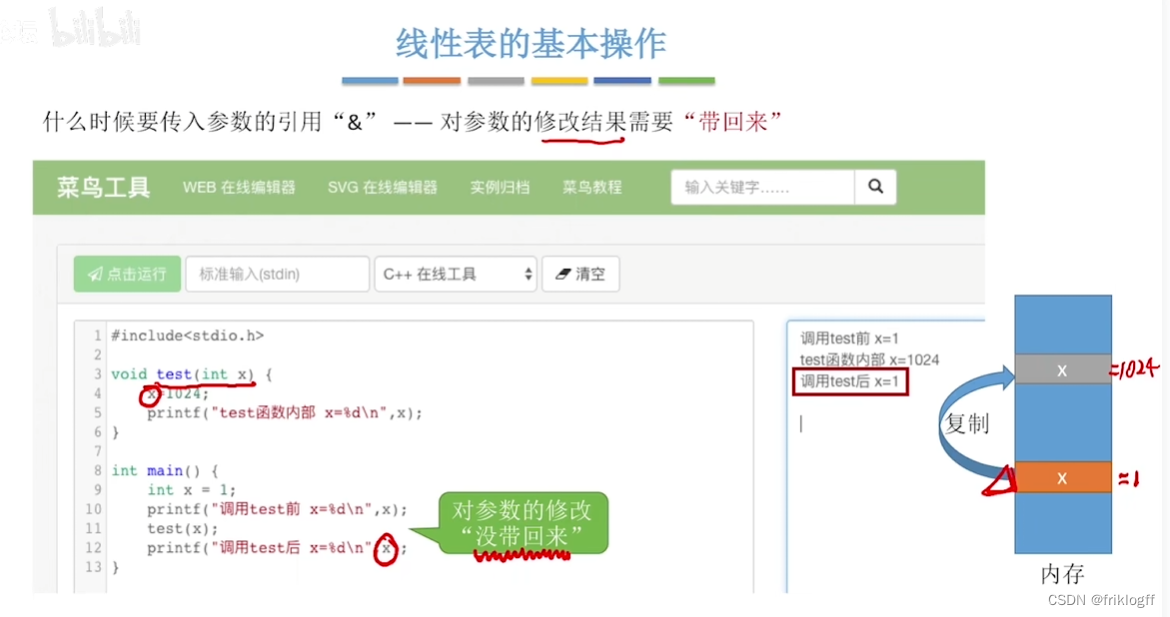
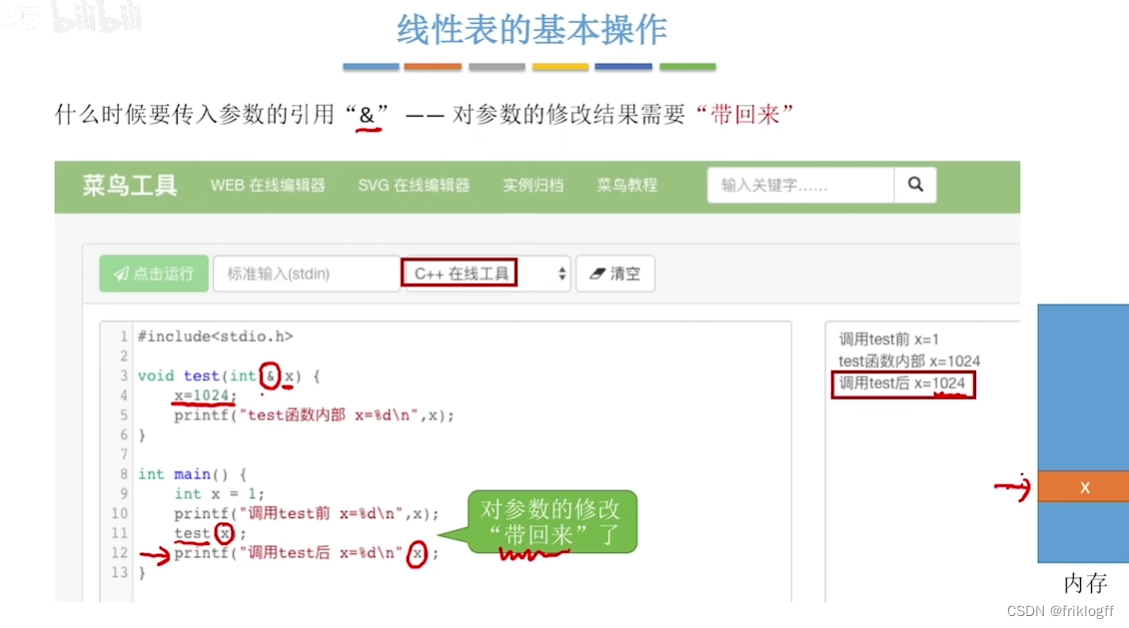
线性表的基本操作

小结
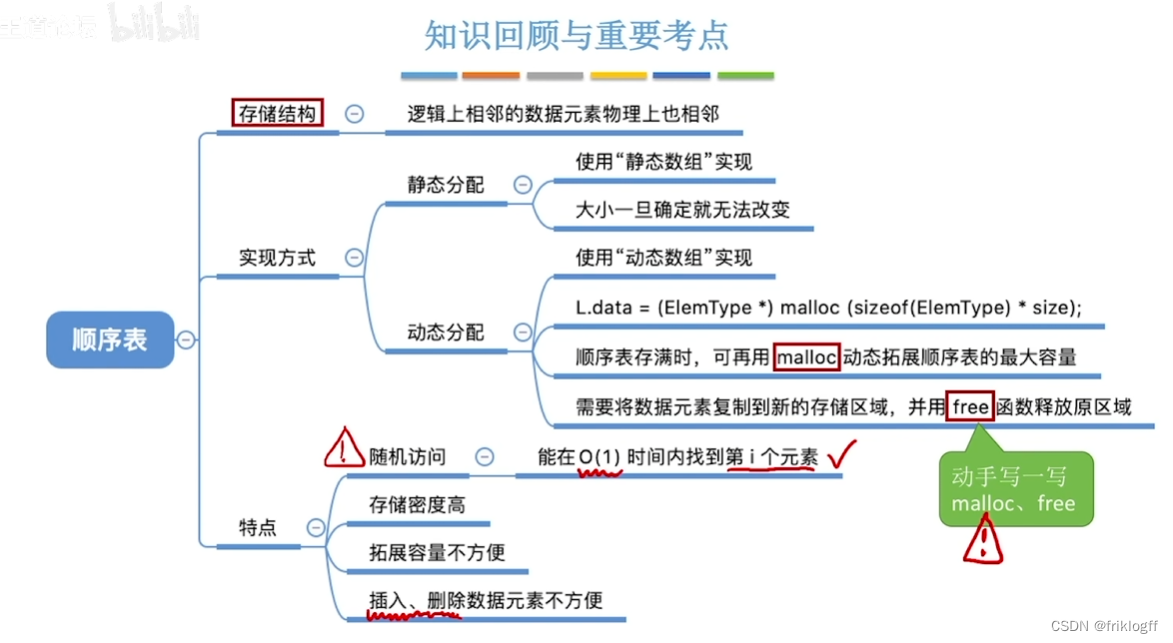
线性表的存储/物理结构
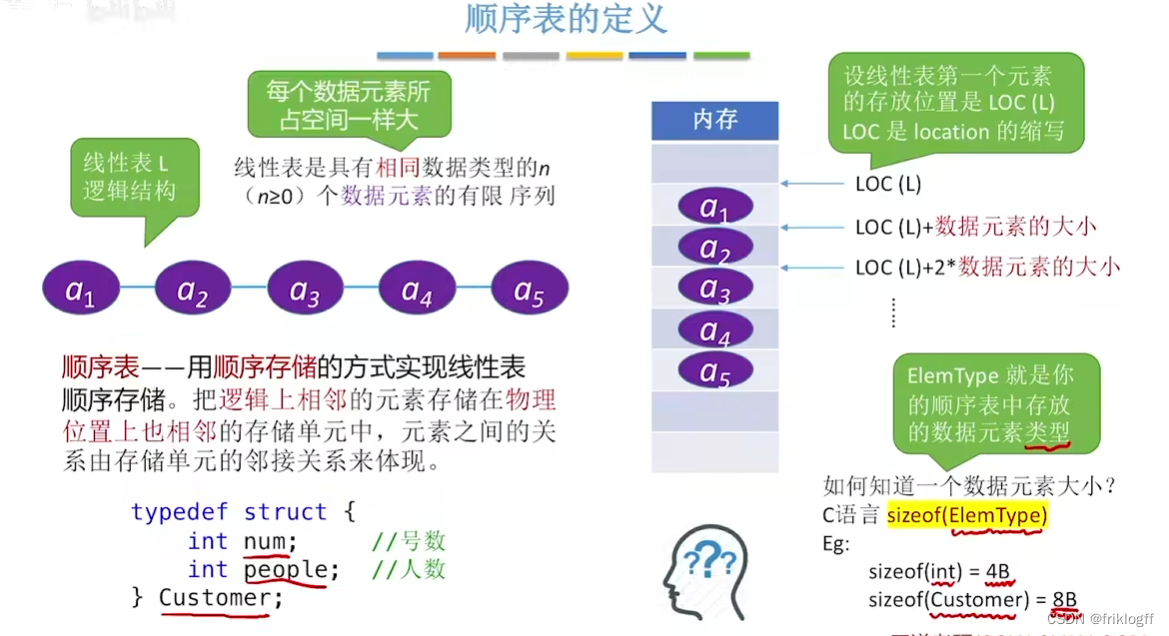
顺序表示(顺序存储结构/顺序映像)

顺序存储定义:把逻辑上相邻的数据元素存储在物理上相邻的存储单元中的存储结构
- 简言之:逻辑上相邻,物理上也相邻
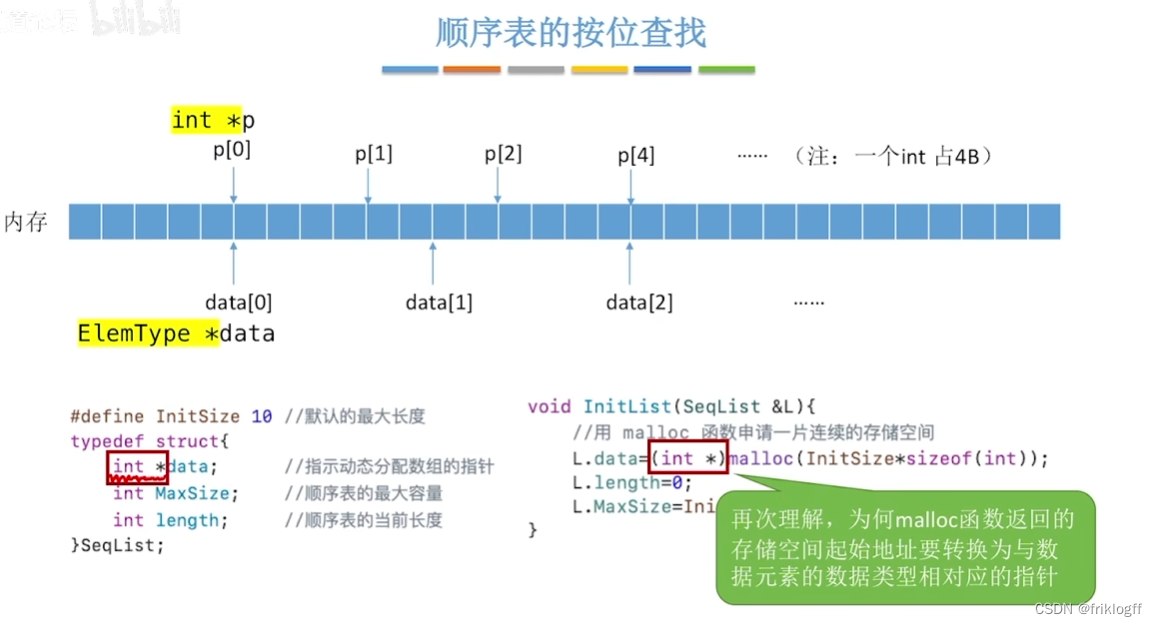
定义实现
-
静态分配
- 类型定义

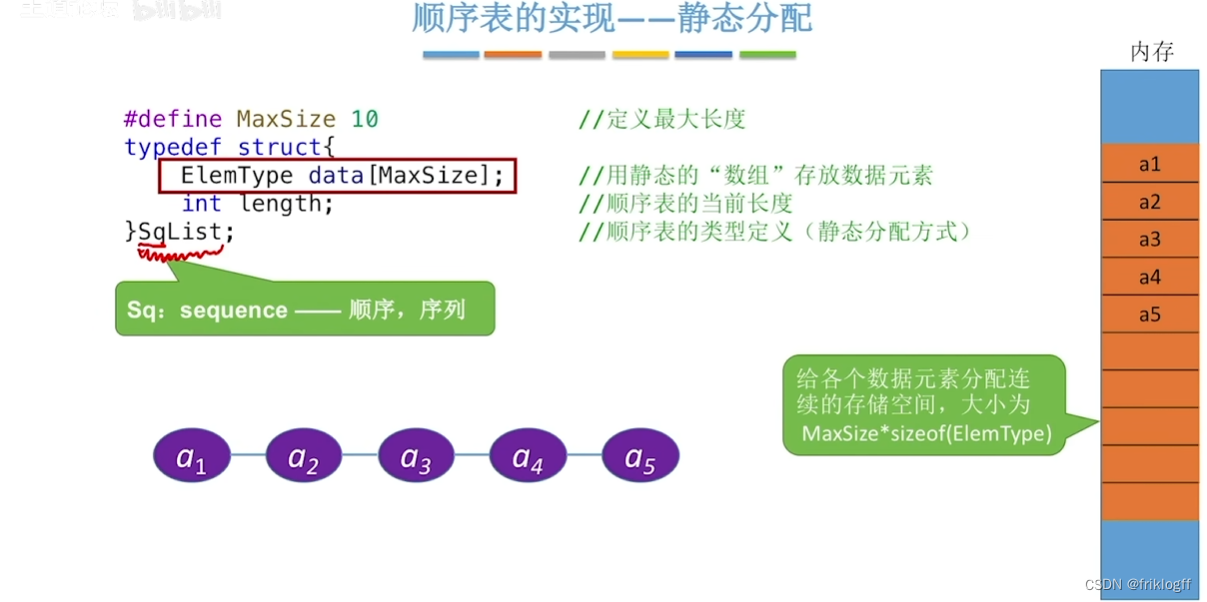
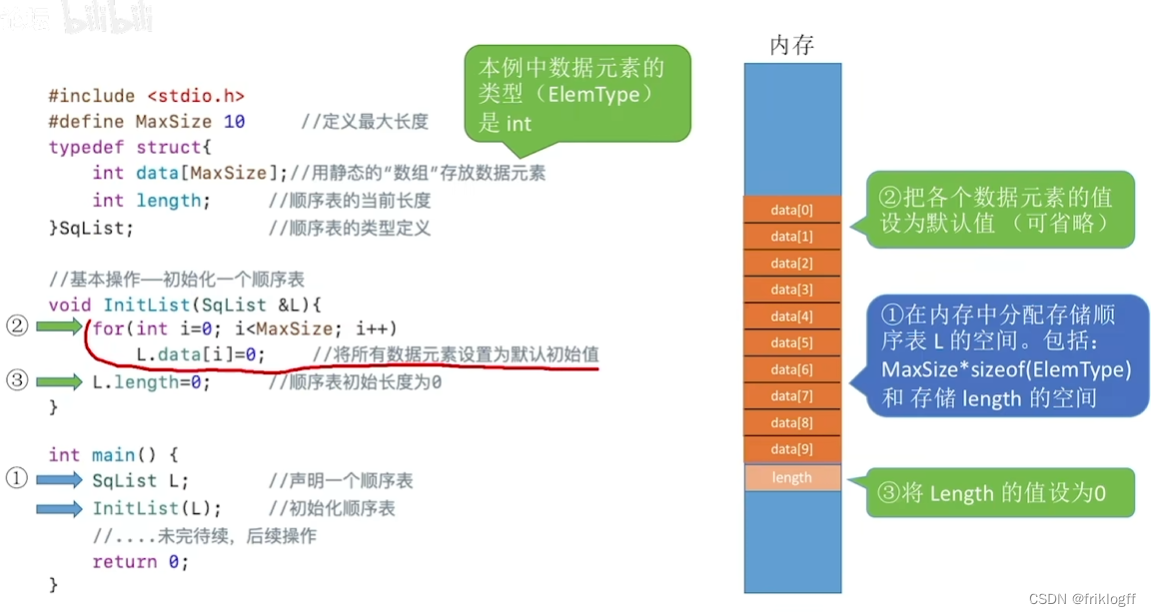
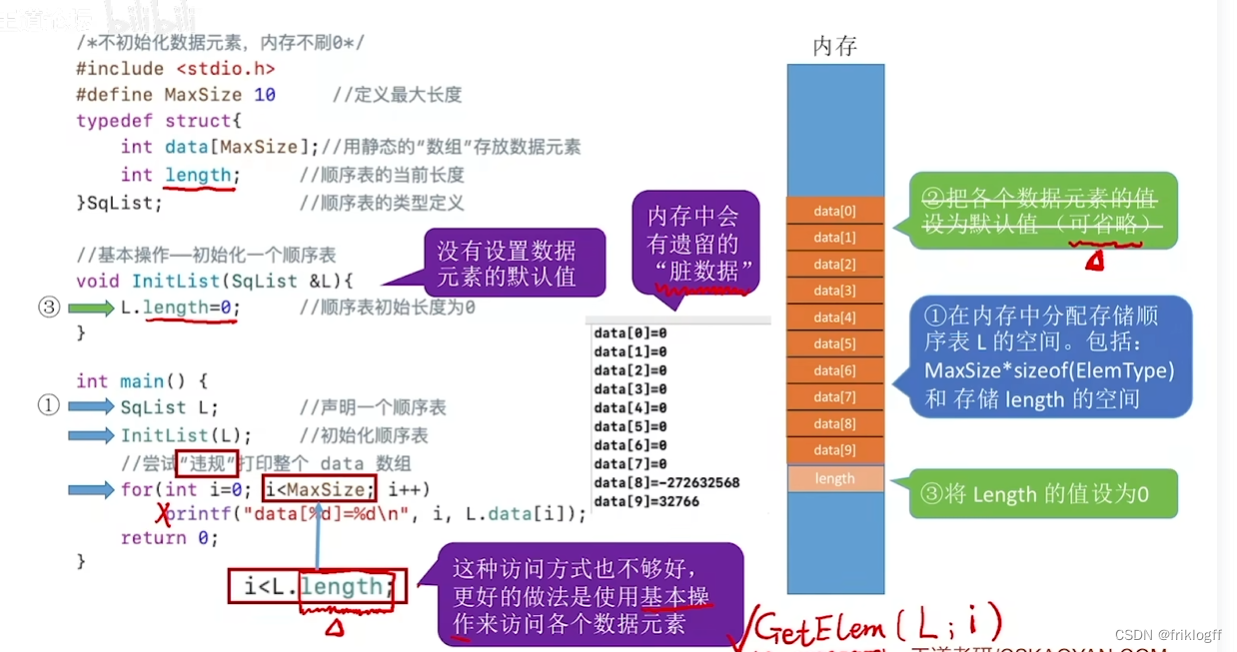
- 类型定义
-
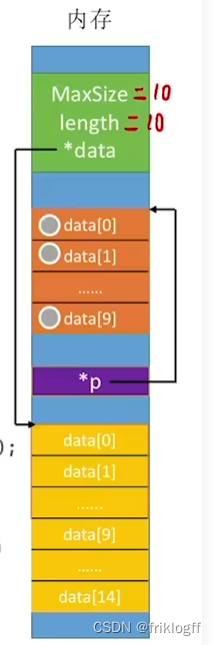
动态分配
-
类型定义

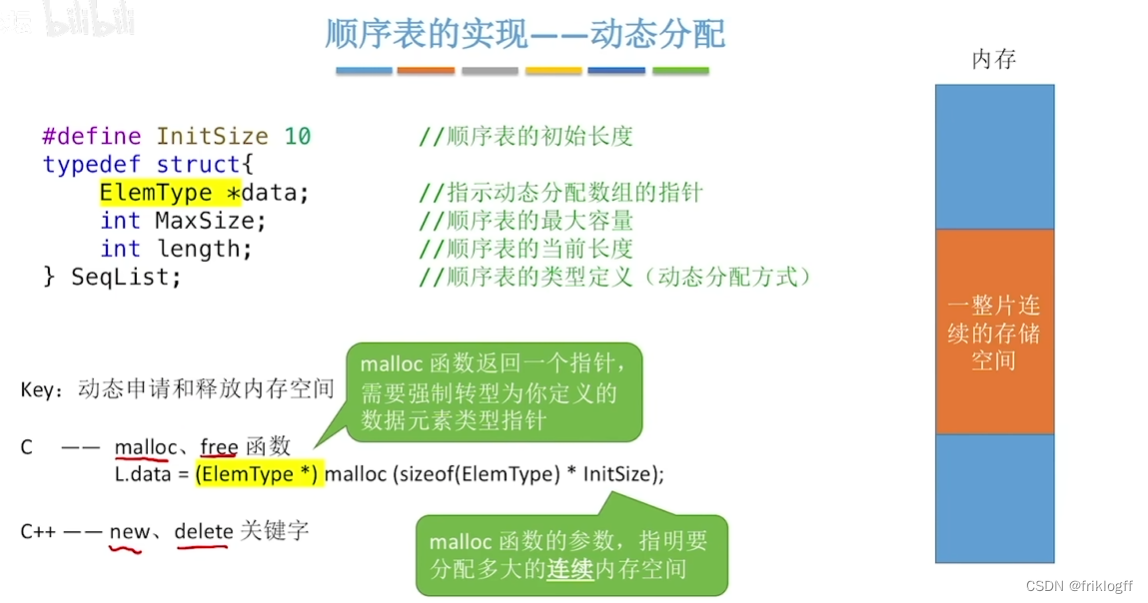

-
//定义变量SqList L; //实现L.data=(ElemType*)malloc(sizeof(ElemType)*MaxSize); //C语言L.data=new ElemType[MaxSize];//C++-
C语言
-
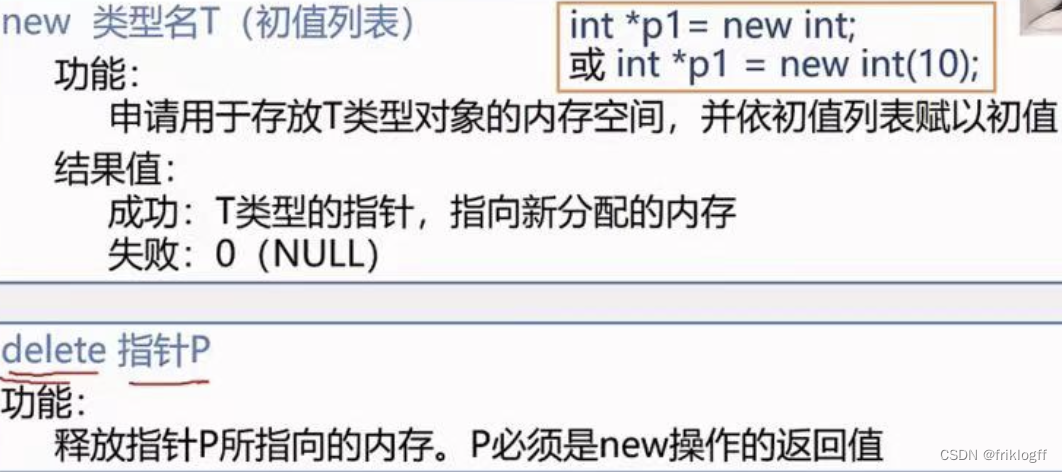
malloc(m)函数:开辟m字节长度的地址空间,并返回这段空间的首地址
-
sizeof(x)运算:计算变量x的长度
-
free§函数:释放指针p所指变量的存储空间
-
-
C++
-
-
-
注意:动态分配不是链式存储,它同样属于顺序存储结构,物理结构没有变化,只是分配的空间大小可以在运行时动态决定
-
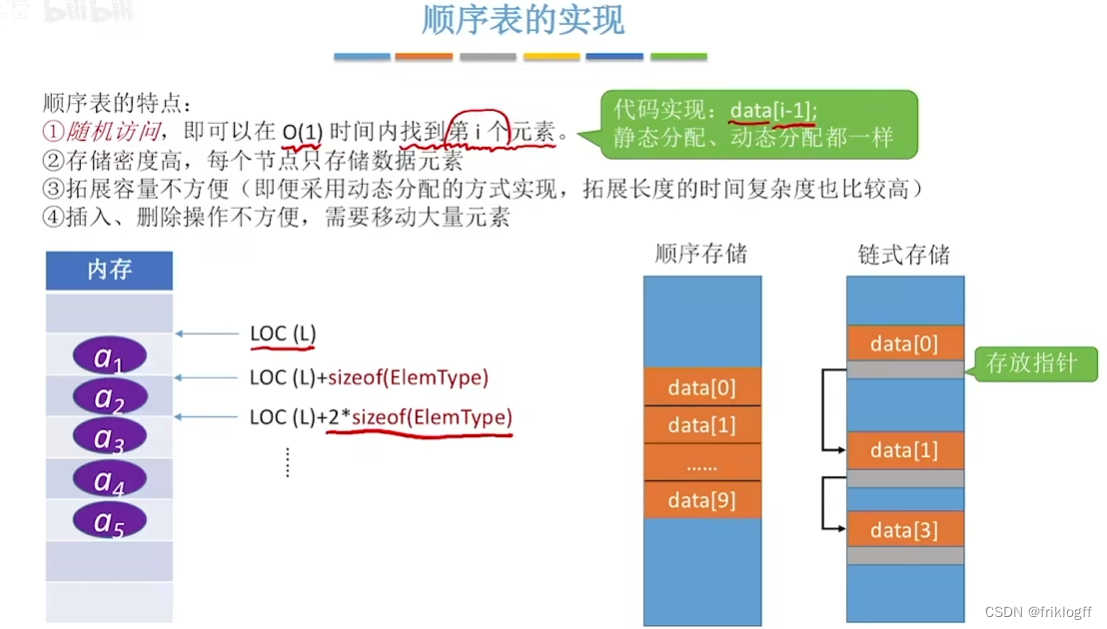
特点
-
以物理位置相邻表示逻辑关系,占用一片连续的存储空间
-
优点
- 随机访问,即通过首地址和元素序号可在时间O(1)内找到指定元素
-
缺点
- 插入、删除元素需要移动大量元素、浪费存储空间、数据元素个数不能自由扩充
小结
基本操作的实现
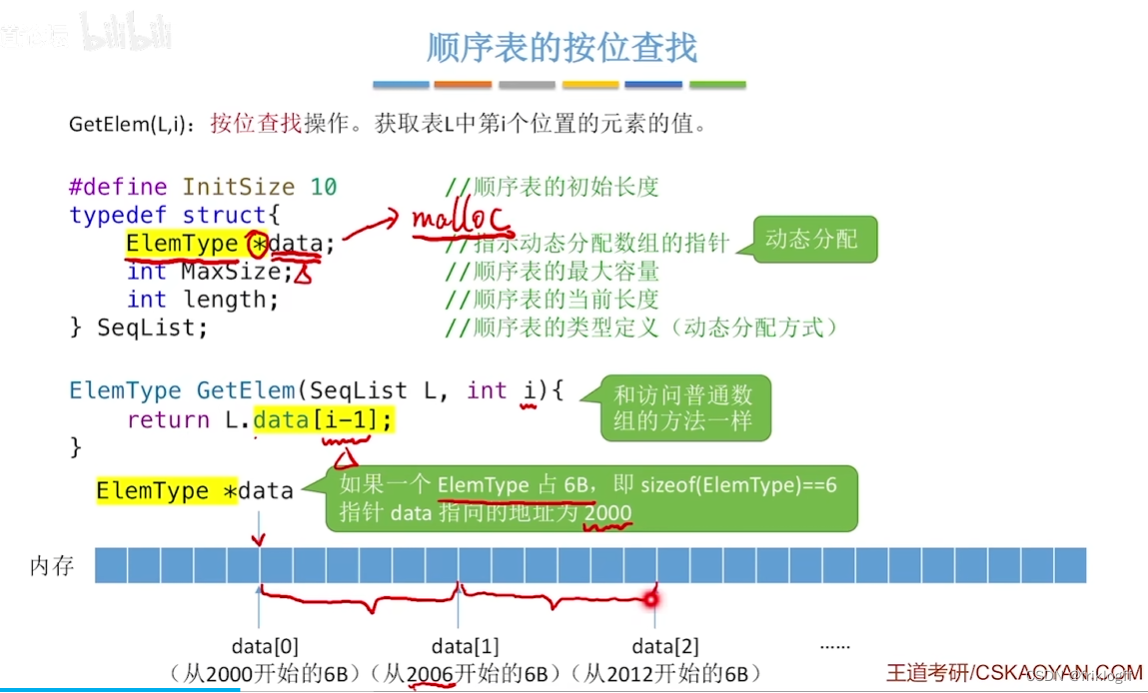
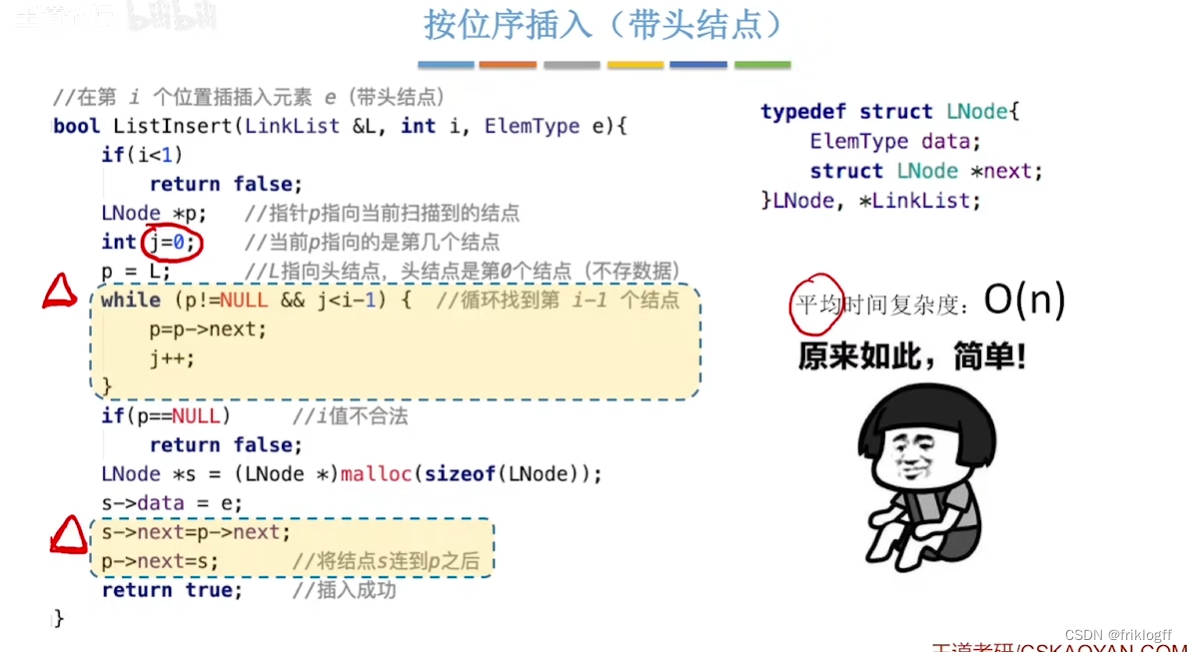
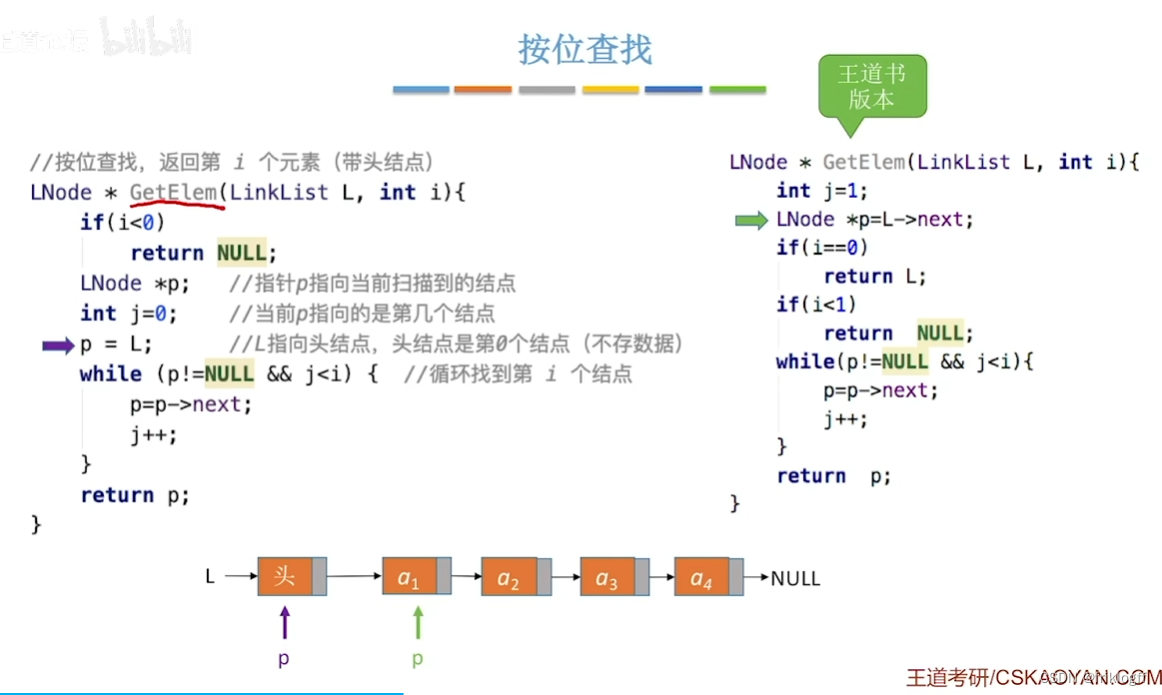
- 注意:线性表元素序号从1开始(逻辑位序和物理位序相差1)
顺序表的基本操作——插入
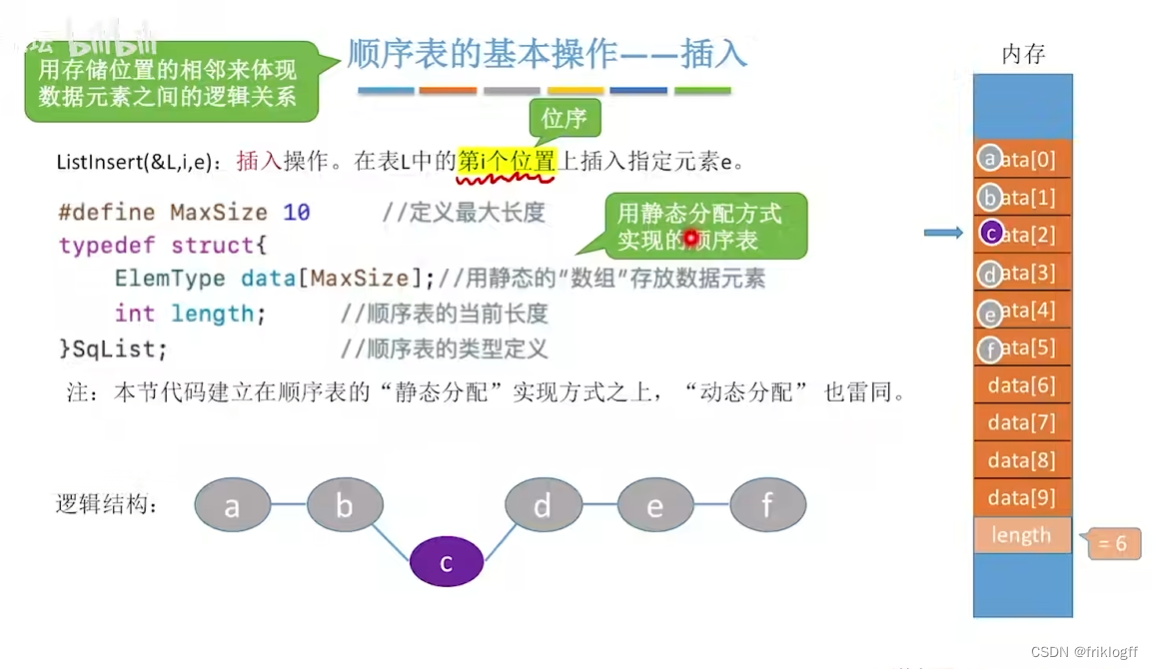
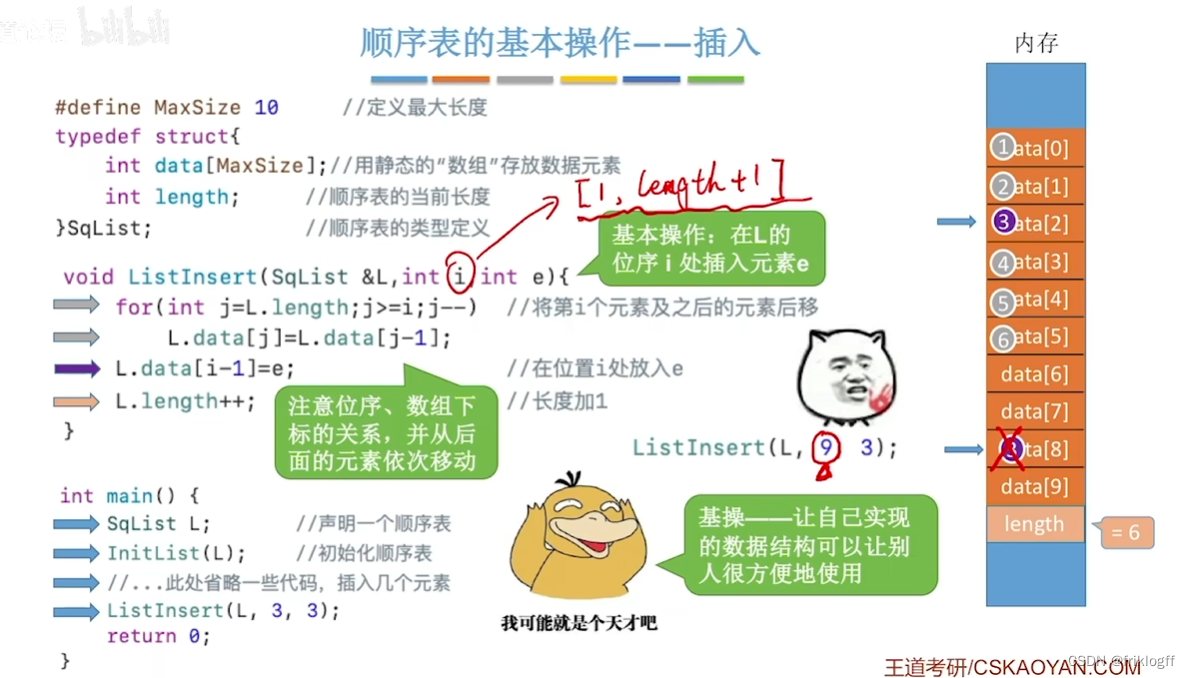
-
插入操作

-
在顺序表的指定位置插入新元素,由于表中元素的物理位置是相邻的,所以当插入新元素的时候就需要对表中的元素进行整体移动
-
插入操作的平均移动次数
- 假设在n+1个位置上插入元素概率为:Pi=1/(n+1)
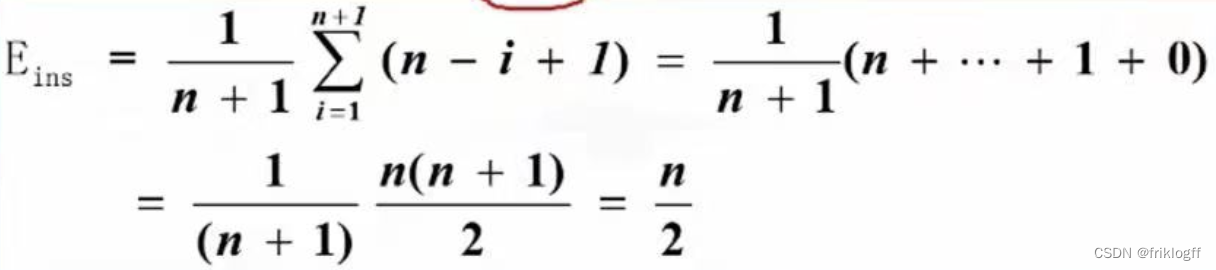
- 假设在n+1个位置上插入元素概率为:Pi=1/(n+1)
-

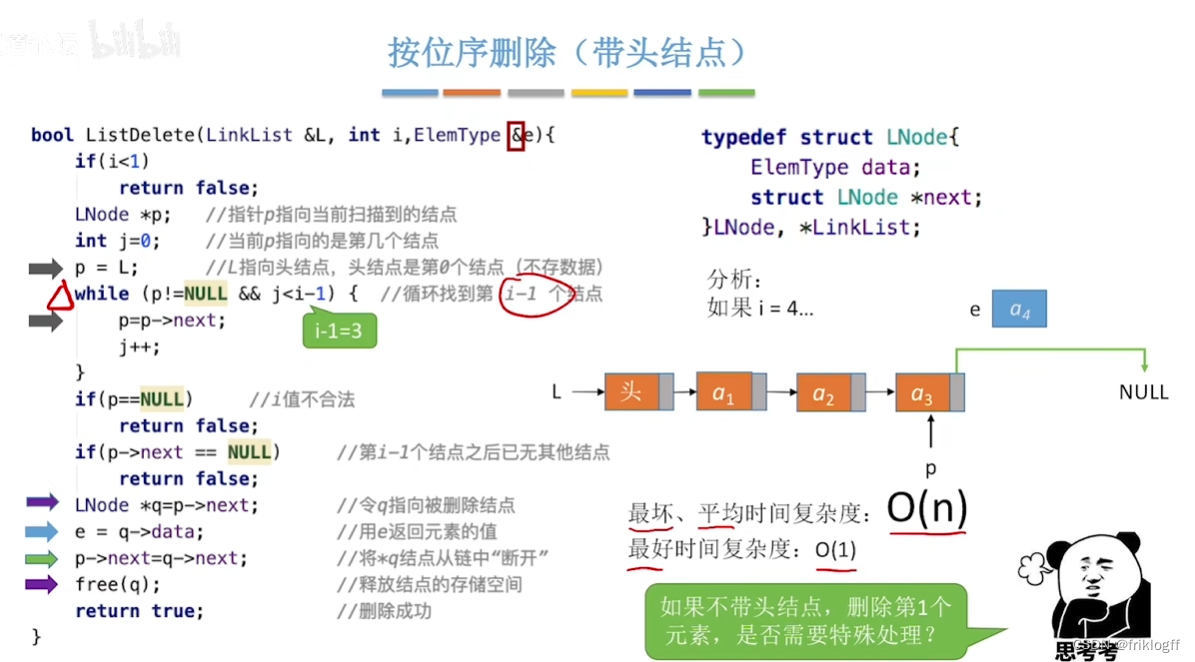
顺序表的基本操作——删除
-
删除操作
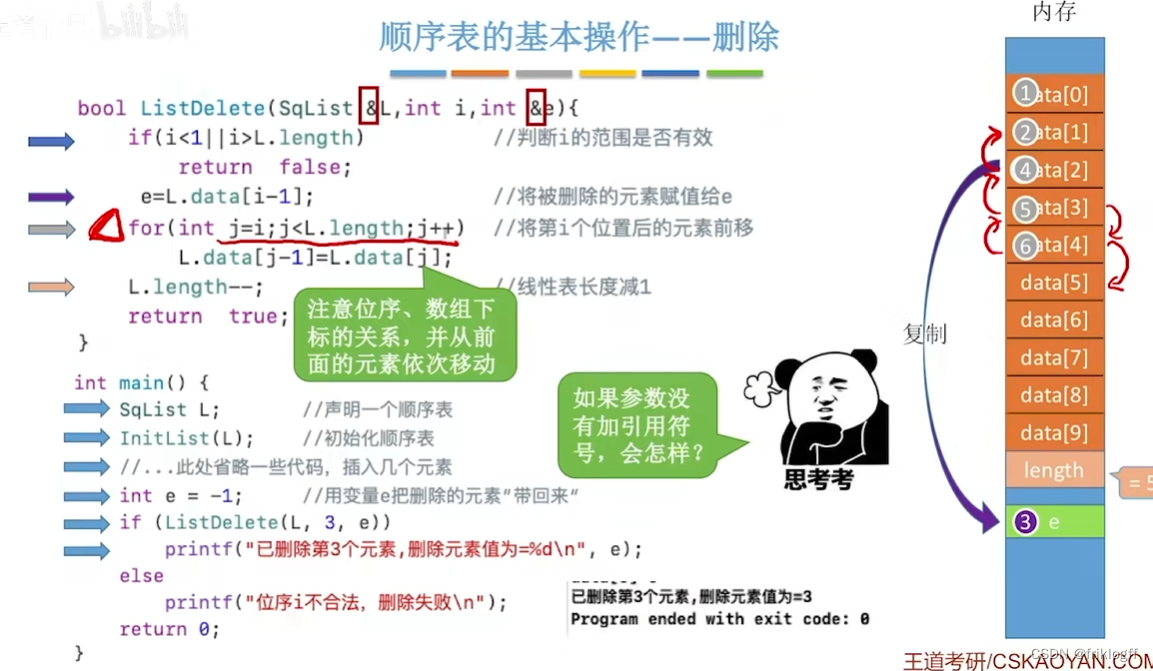
-
删除指定位置元素,将后续元素依次向前移动一个位置
-
删除操作的平均移动次数
- 假设删除第i个元素概率:Pi=1/n
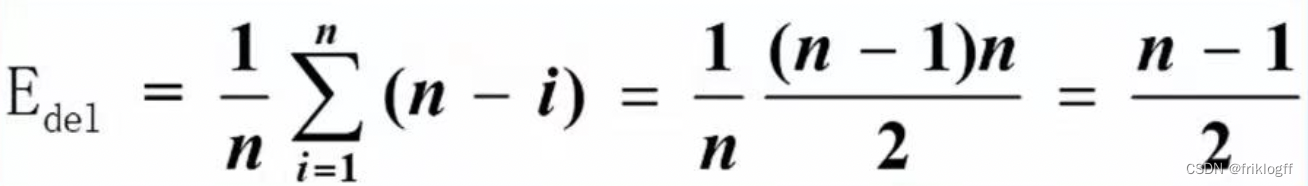

- 假设删除第i个元素概率:Pi=1/n
-
小结
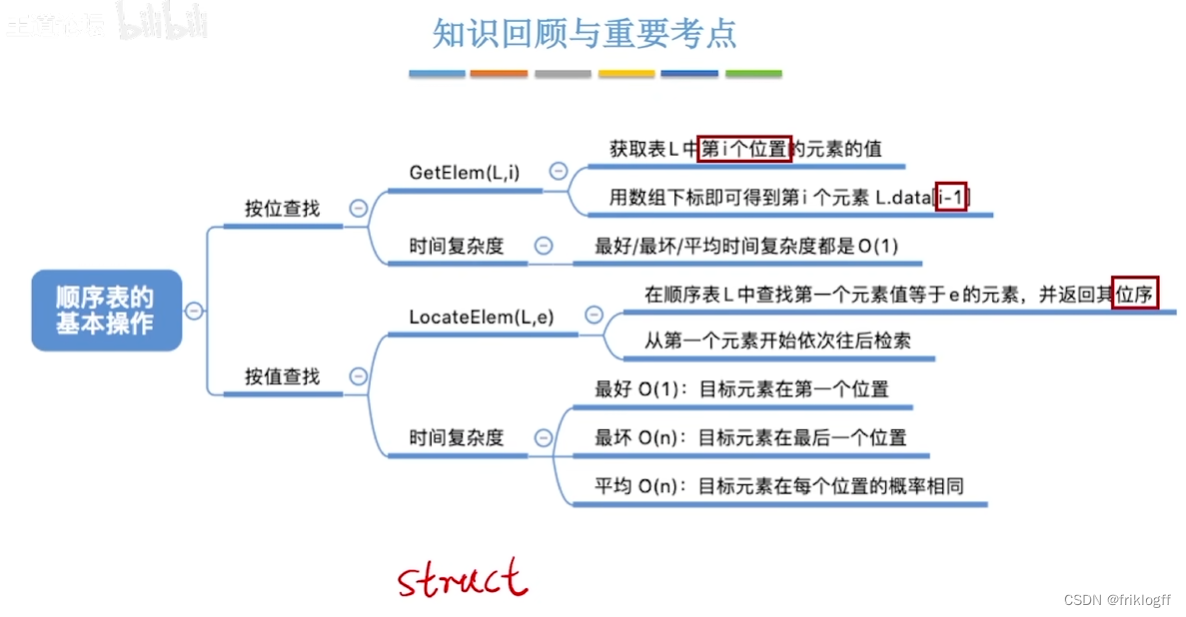
顺序表的基本操作——按位查找
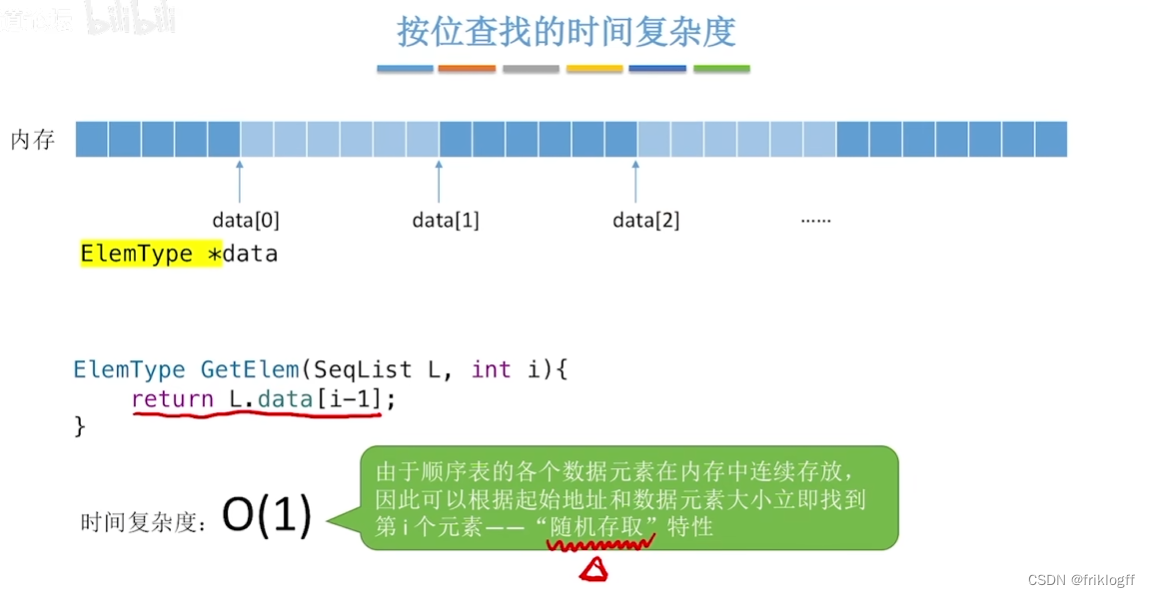
顺序表的基本操作——按值查找

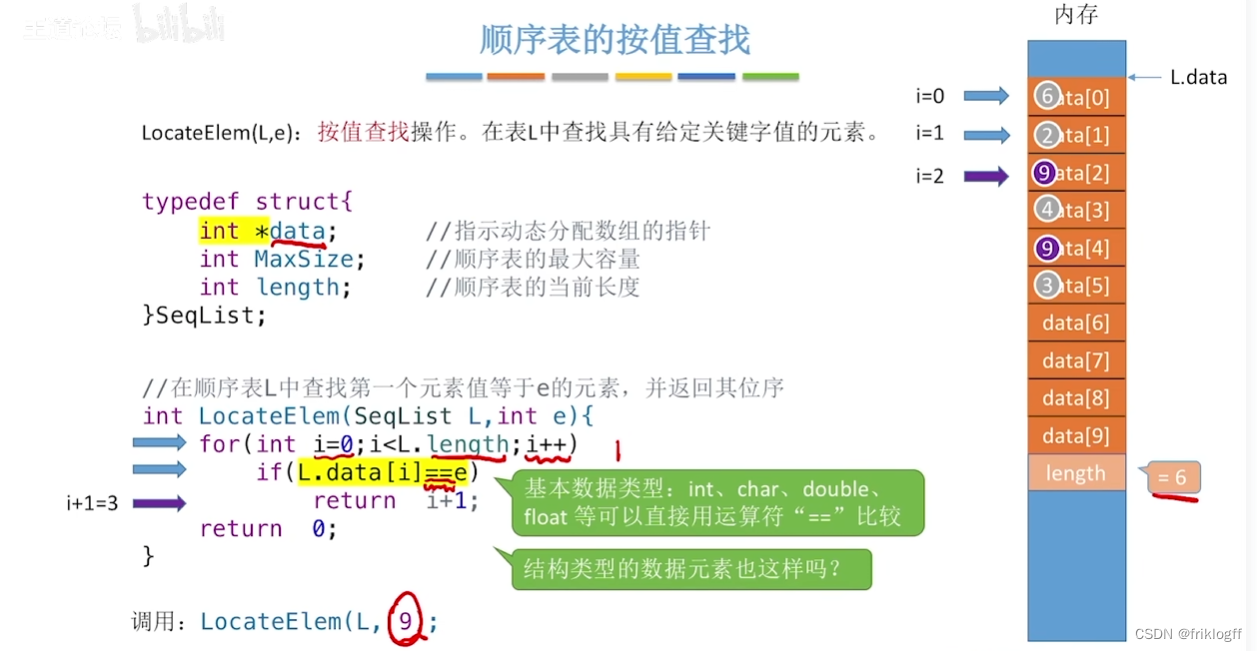

-
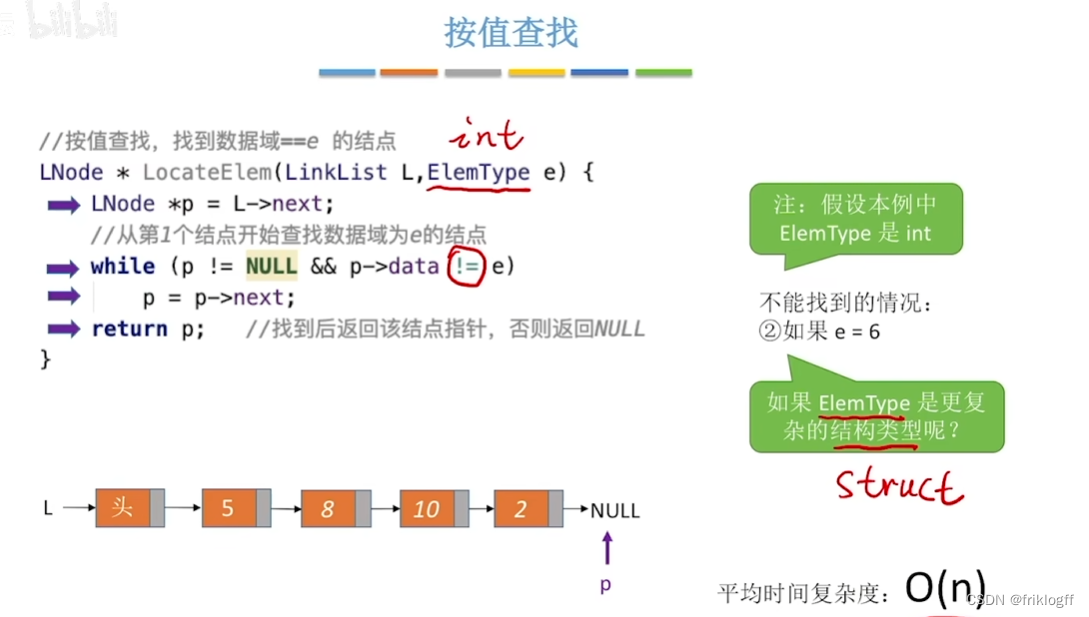
按值查找(顺序查找)
-
在顺序表中查找特定值元素的位置
-
顺序查找的平均查找长度
-
假设每个记录的查找概率相等:Pi = 1/n
-
ASL = P1 + 2P2 + … + (n-1)Pn-1 + nPn = 1/n×(1+2+…+n)=1/n × n(n+1)/2 = (n+1)/2

-
-
小结
链式表示
用一组物理位置任意的存储单元来存放线性表的数据元素(逻辑次序和物理次序不一定相同)
特点
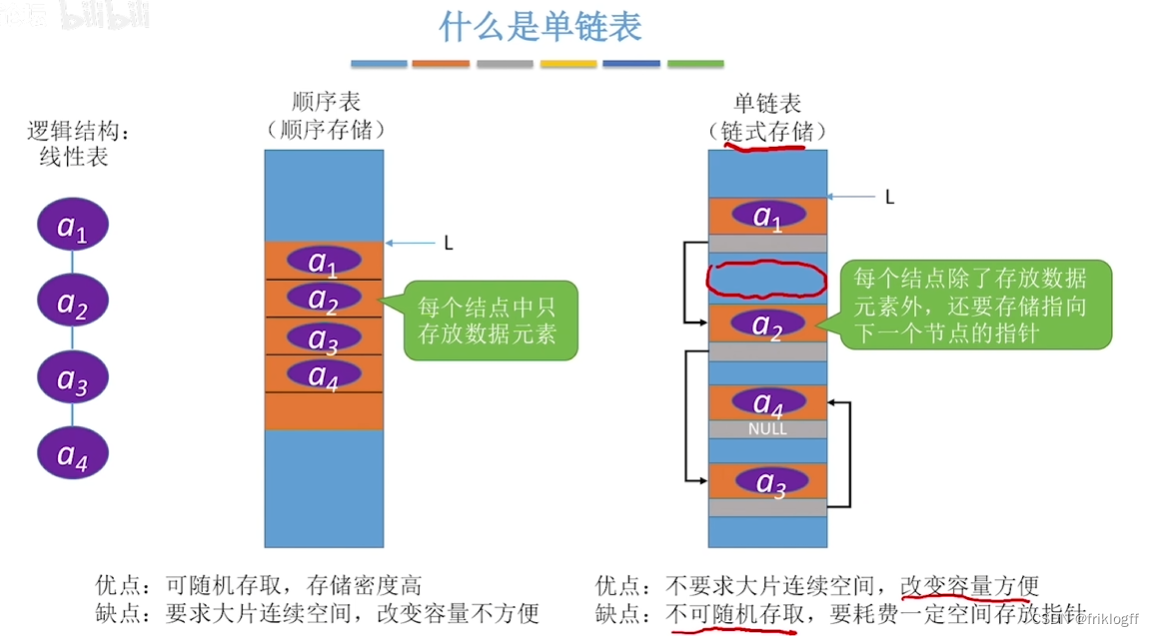
-
优点
- 解决顺序表大量连续存储单元的缺点,插入和删除操作无需移动元素
-
缺点
- 指针域浪费空间、查找操作需要从头遍历(顺序查找方式)
结构
-
结点
-
数据元素的存储映像,由数据域和指针域组成
-
数据域data:存储元素数值数据
-
指针域next:存储直接后继结点的存储位置
-
-
-
头指针
- 用来标识单链表,始终指向单链表第一个结点
-
头结点
-
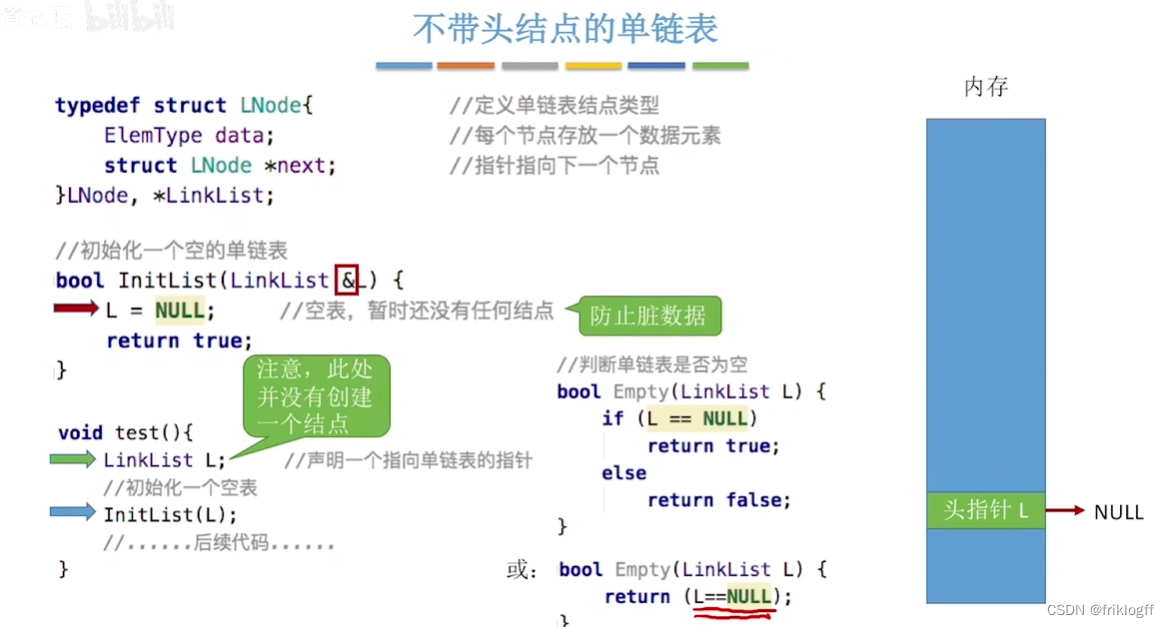
-
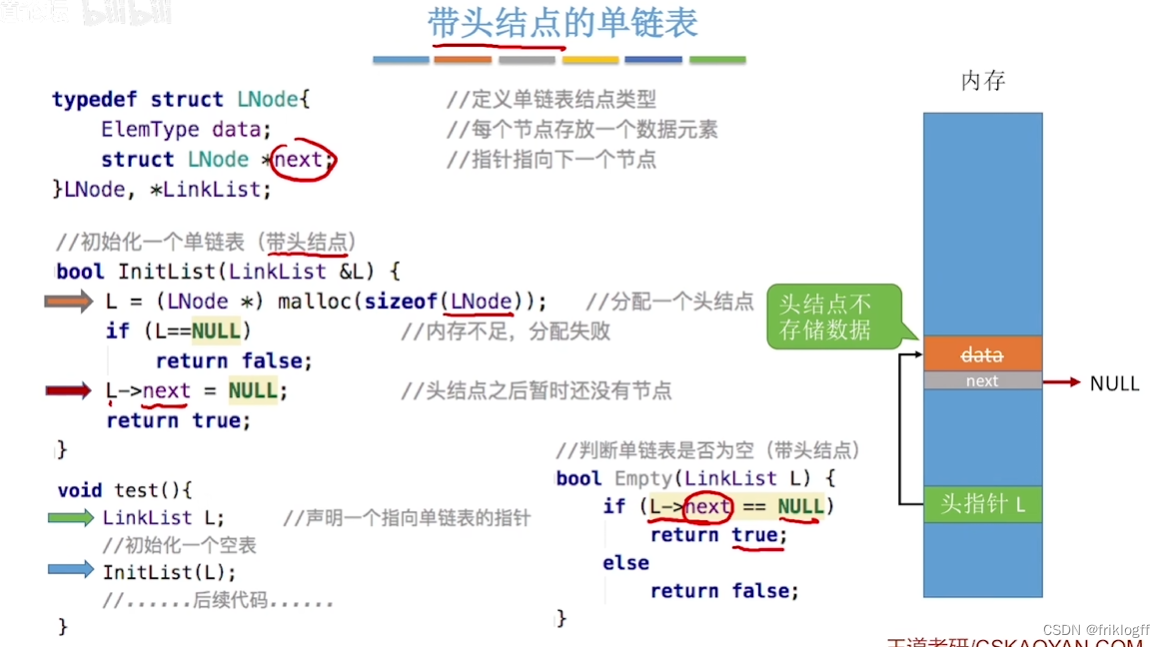
-
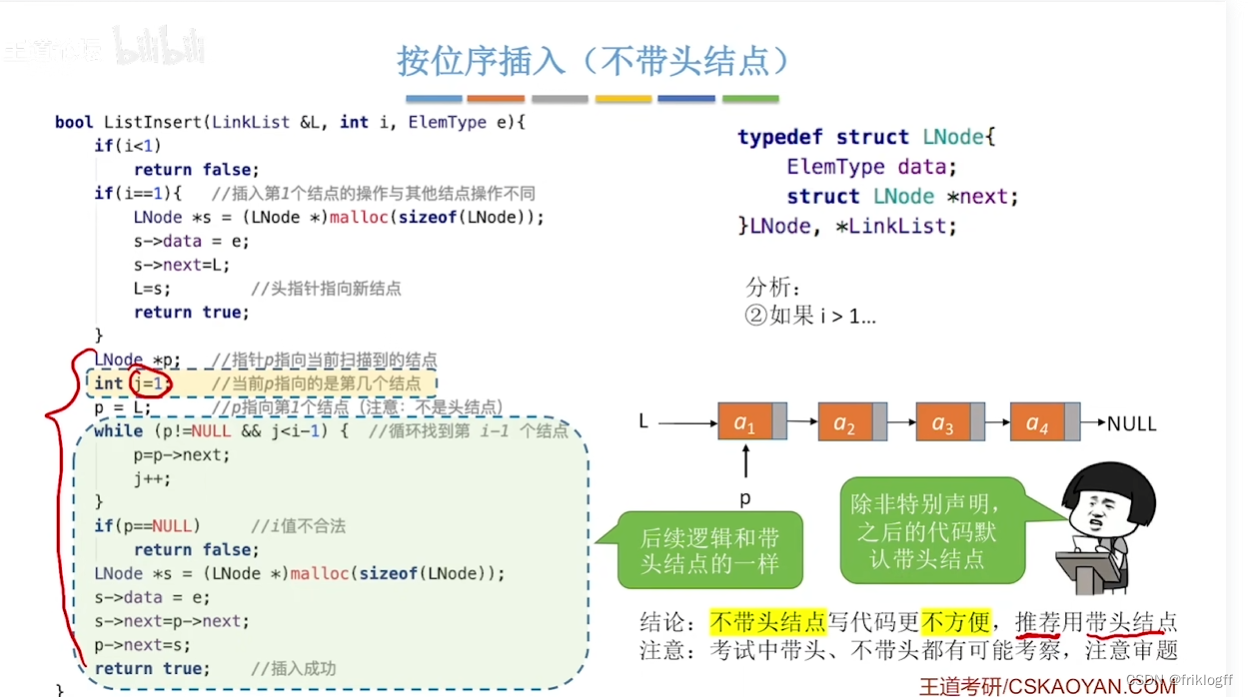
单链表第一个结点前附加一个结点,头结点数据域可以不设任何信息,也可以记录表长等
- 引入头结点后,第一个数据结点和其他数据结点的操作一致,无需特殊处理;且空表和非空表的处理得到统一
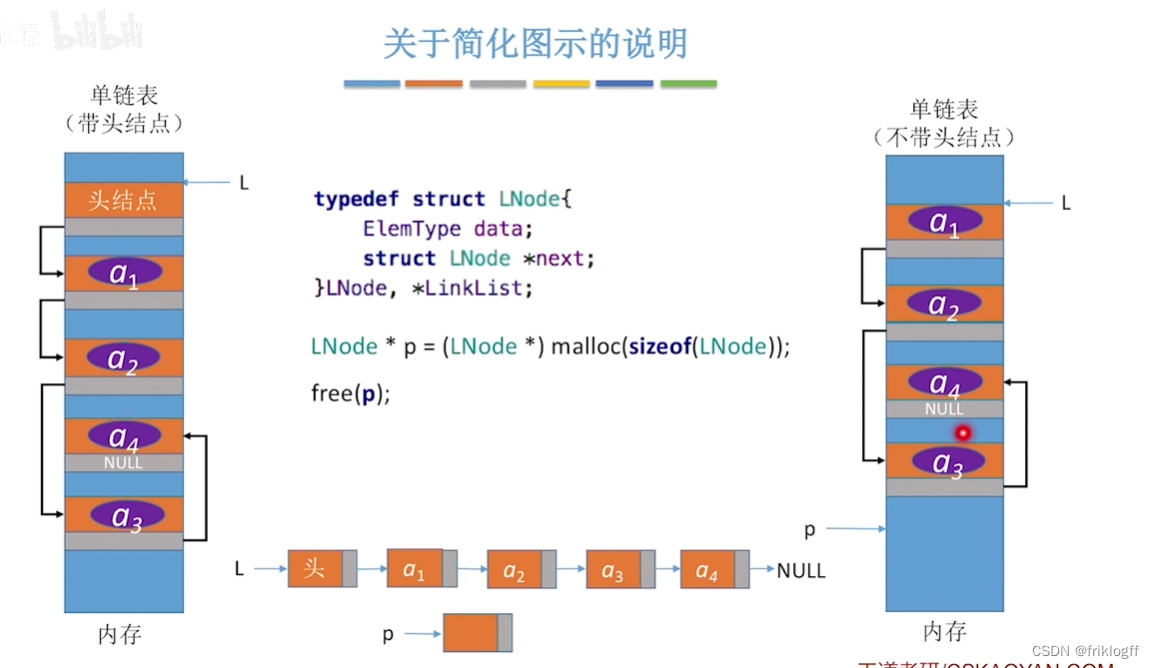
- 引入头结点后,第一个数据结点和其他数据结点的操作一致,无需特殊处理;且空表和非空表的处理得到统一
-
小结
单链表
-
定义实现
-
结点类型和链表指针定义

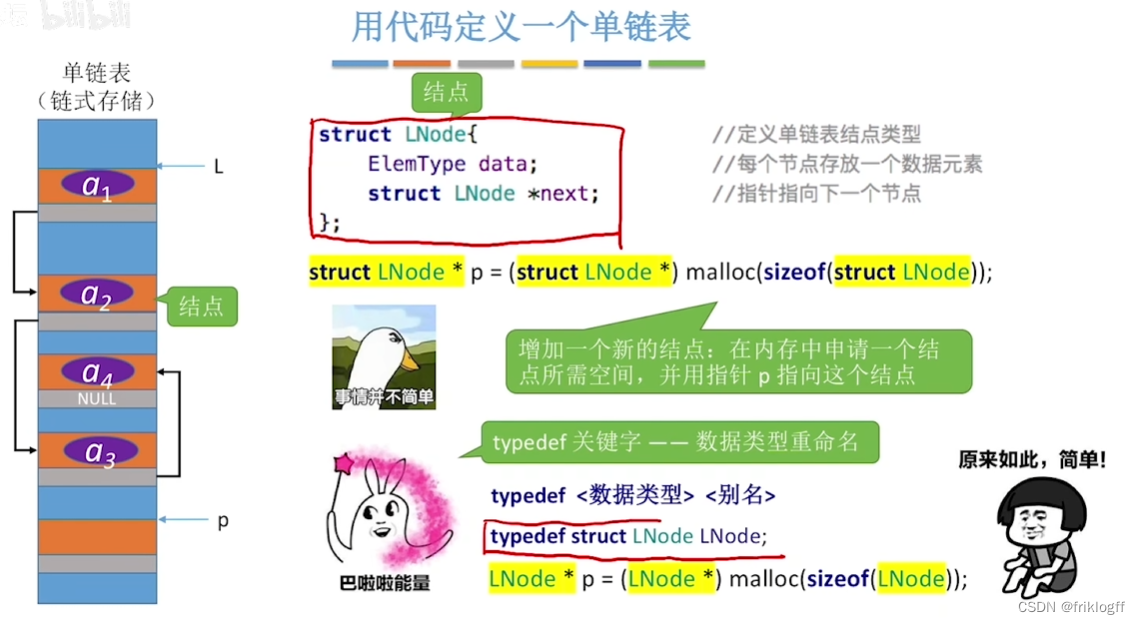
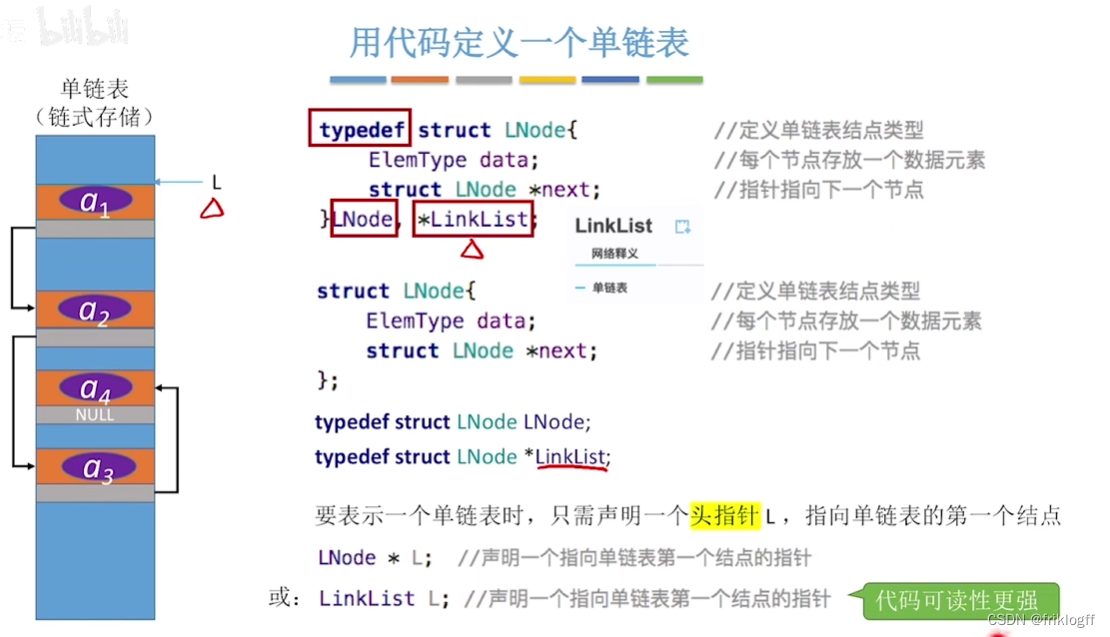
- 定义链表L:LinkList L;
定义结点指针p:LNode *P;

- 定义链表L:LinkList L;
-
插入
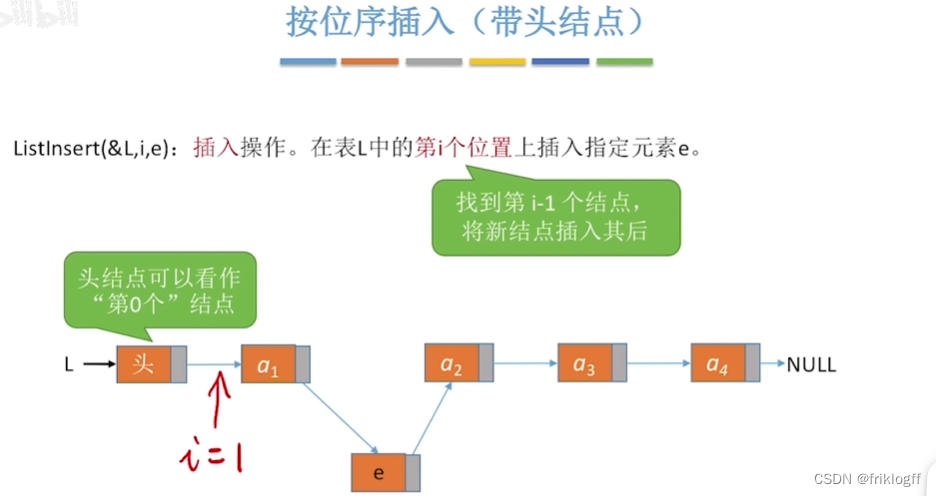
删除
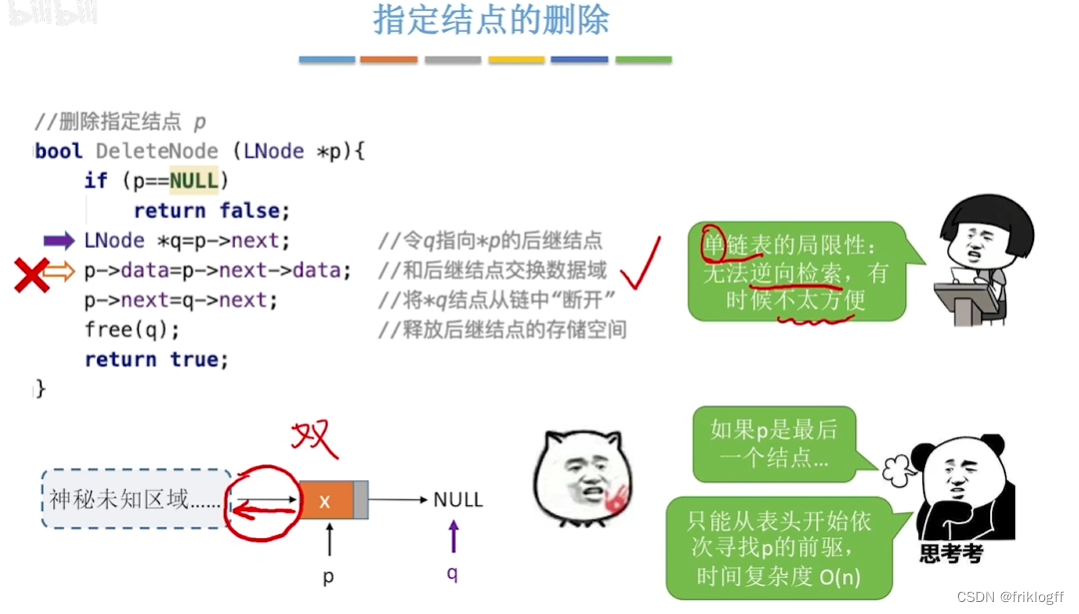
小结

查找

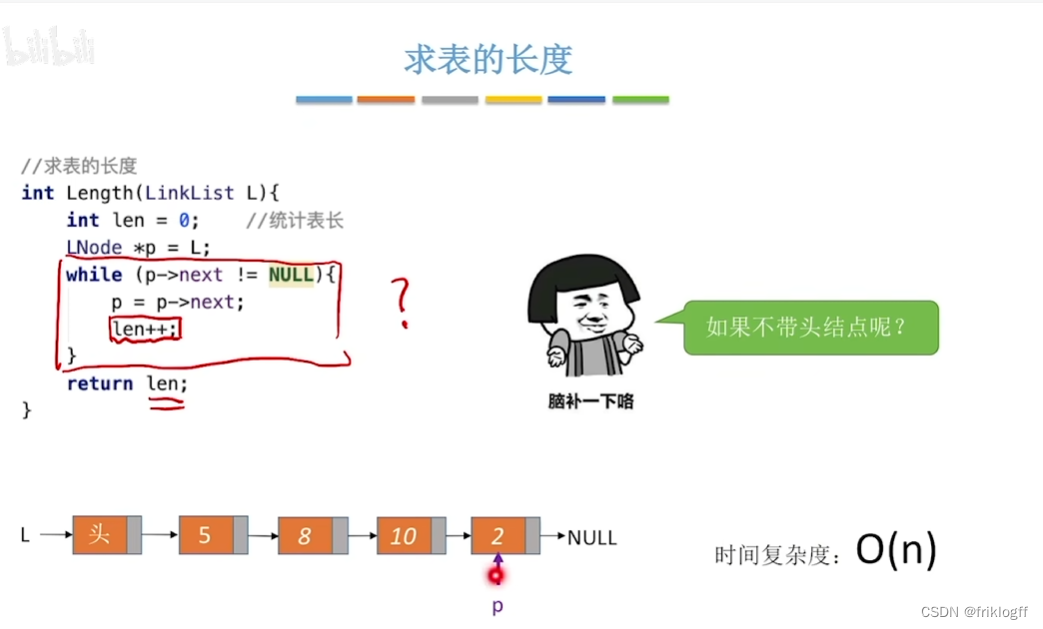
小结
单链表建立
-
操作
-
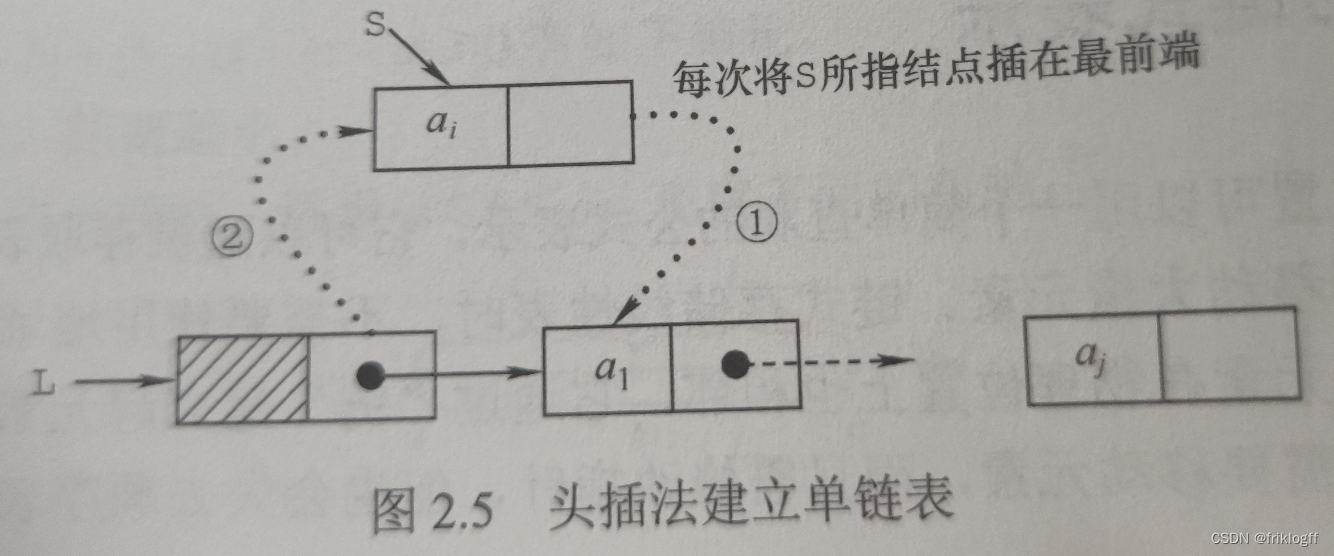
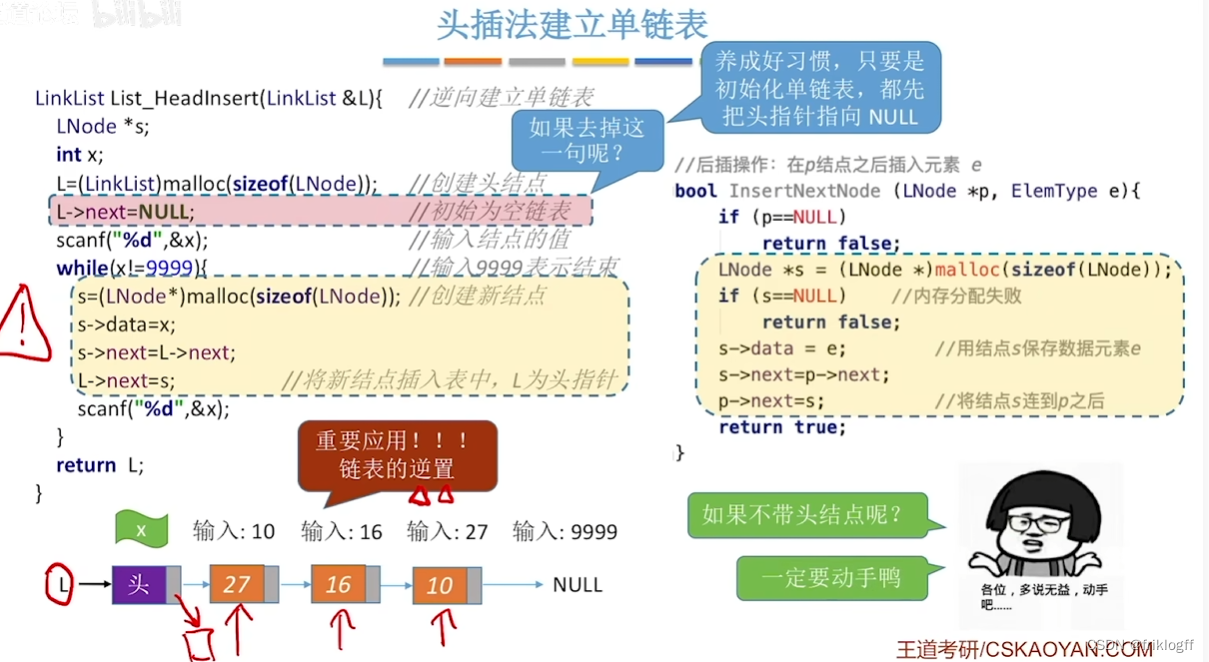
头插法建立单链表
-
-
从一个空表开始,生成新结点,插入到当前链表的表头,即头结点之后
-
注意:生成的链表中结点的次序和输入数据顺序相反,可以利用该特点进行链表转置
-
-
-
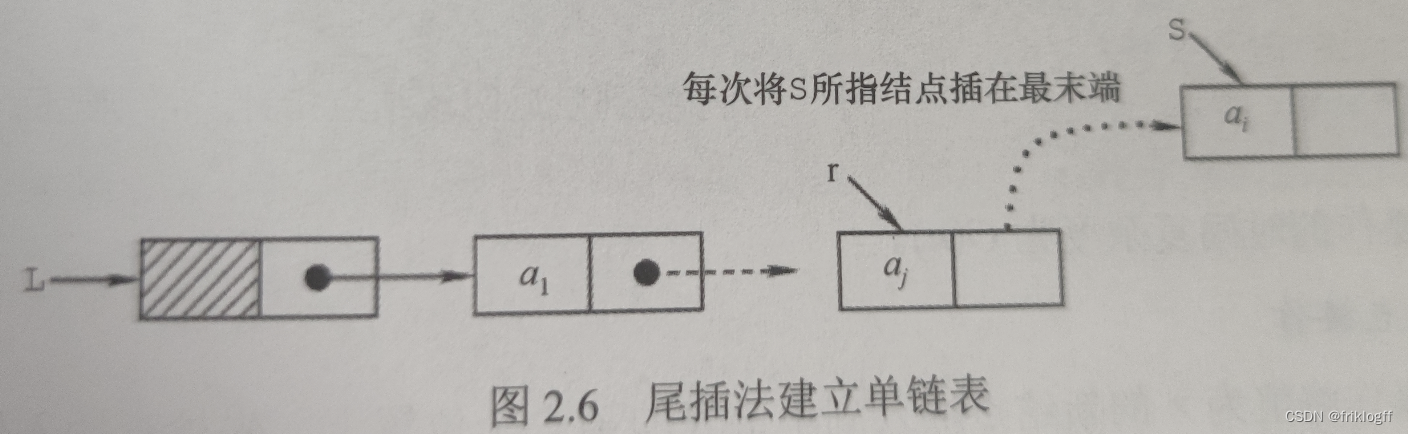
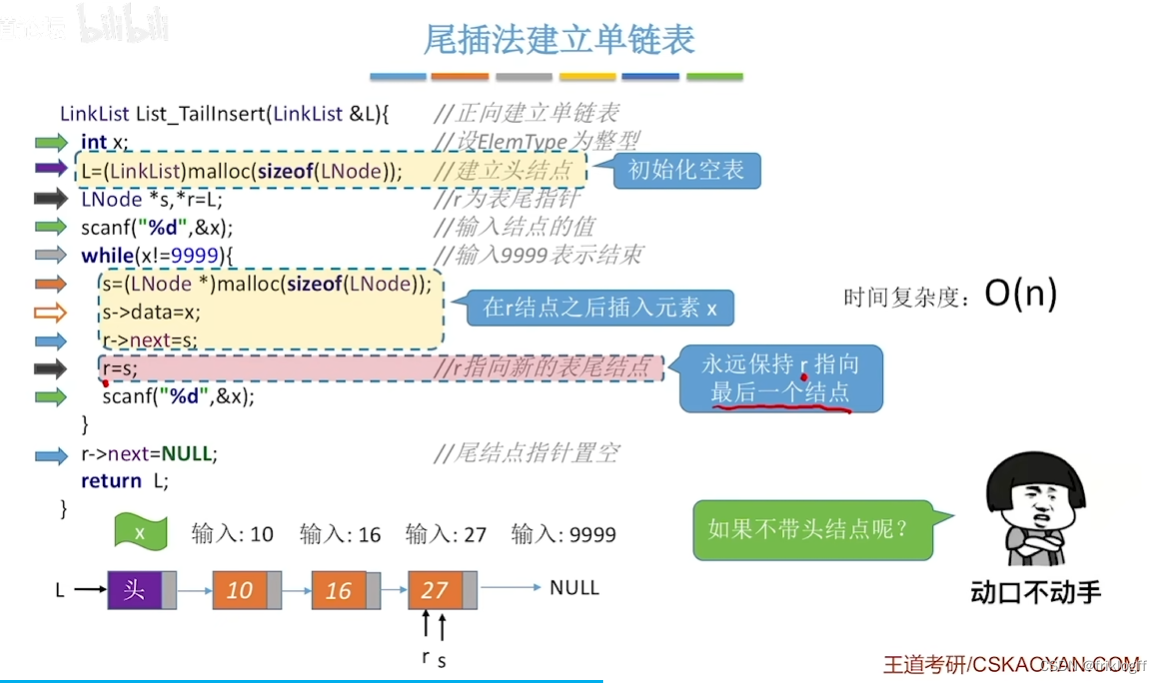
尾插法建立单链表
-
-
将新结点插入到链表的表尾,为此需增加一个尾指针
-
产生链表结点次序和输入数据顺序一致
-
-
-
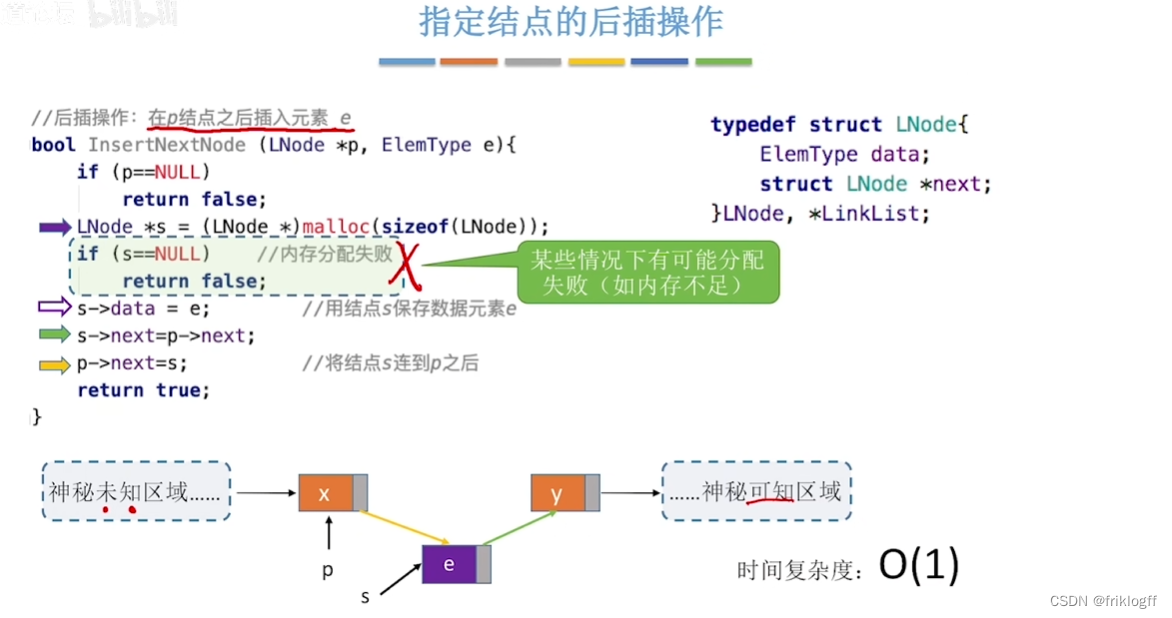
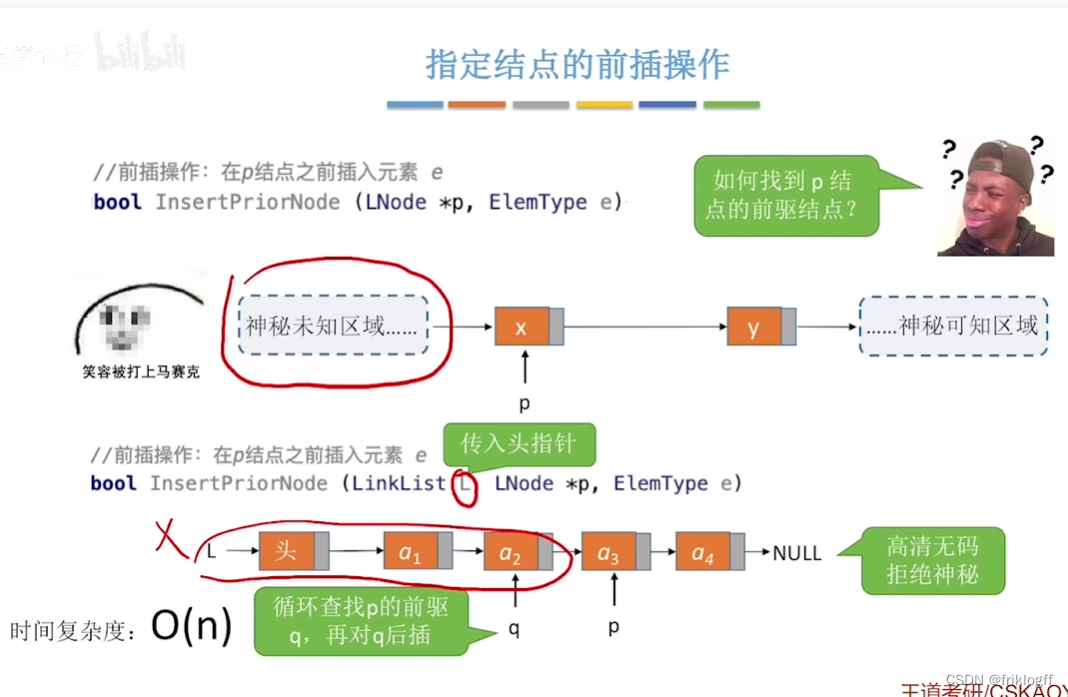
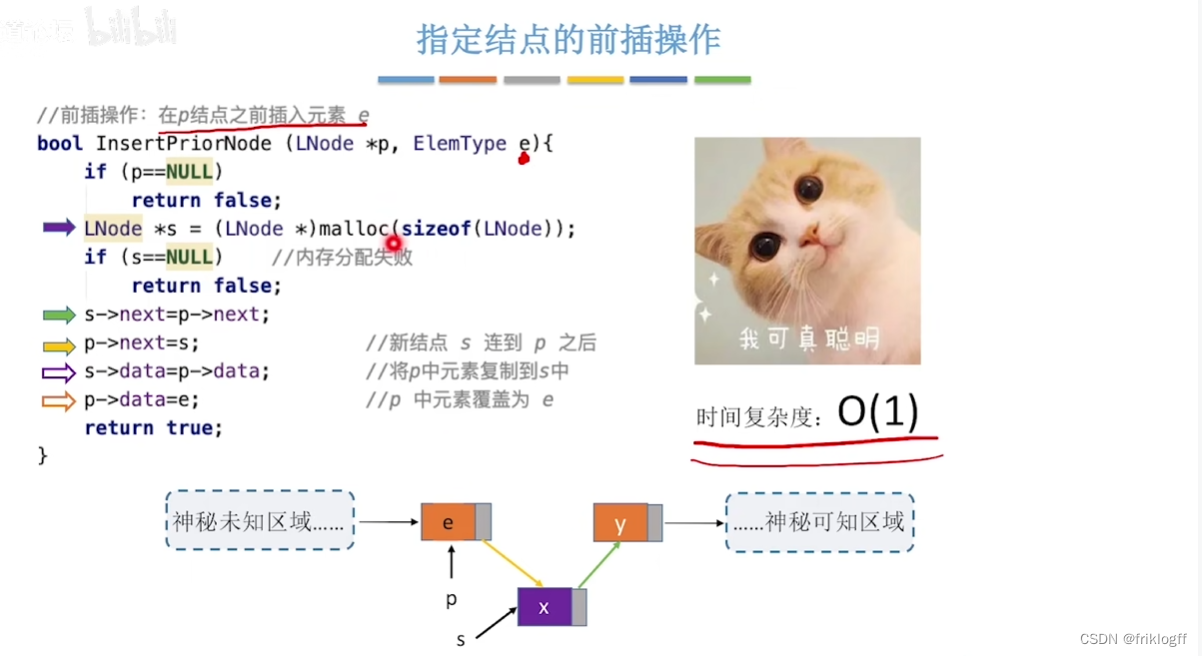
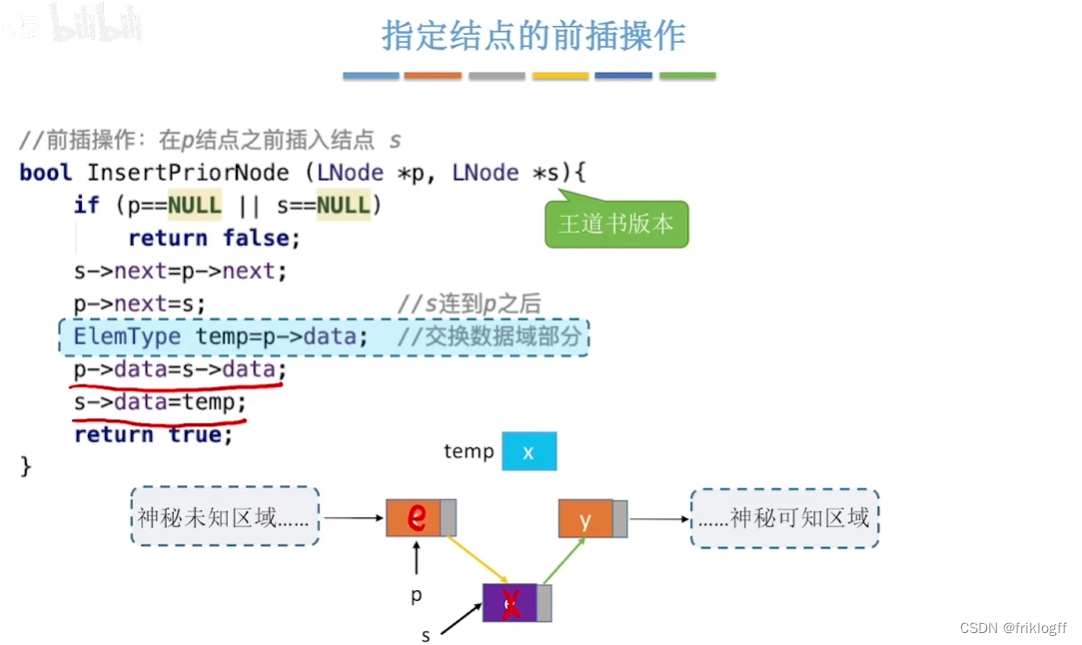
对结点S进行前插操作
-
新建结点X连在结点S后
- 交换X与S中数据
-
-
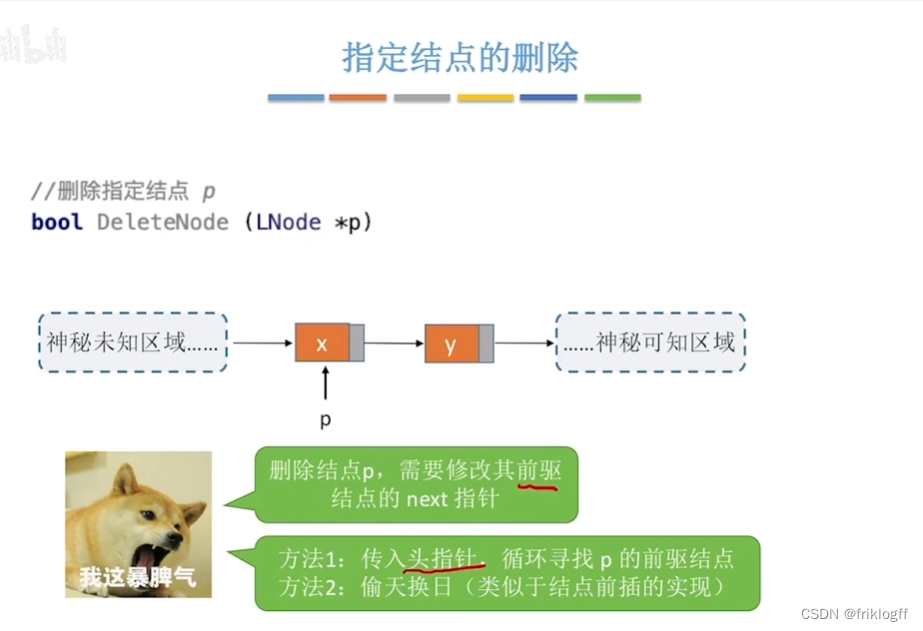
其他操作略(查找、插入、删除、求表长)
-
本质上只要学会结点链表定义,其他操作都是对指针的操作,弄清楚箭头顺序即可,原则是确保不会造成断链和结点丢失
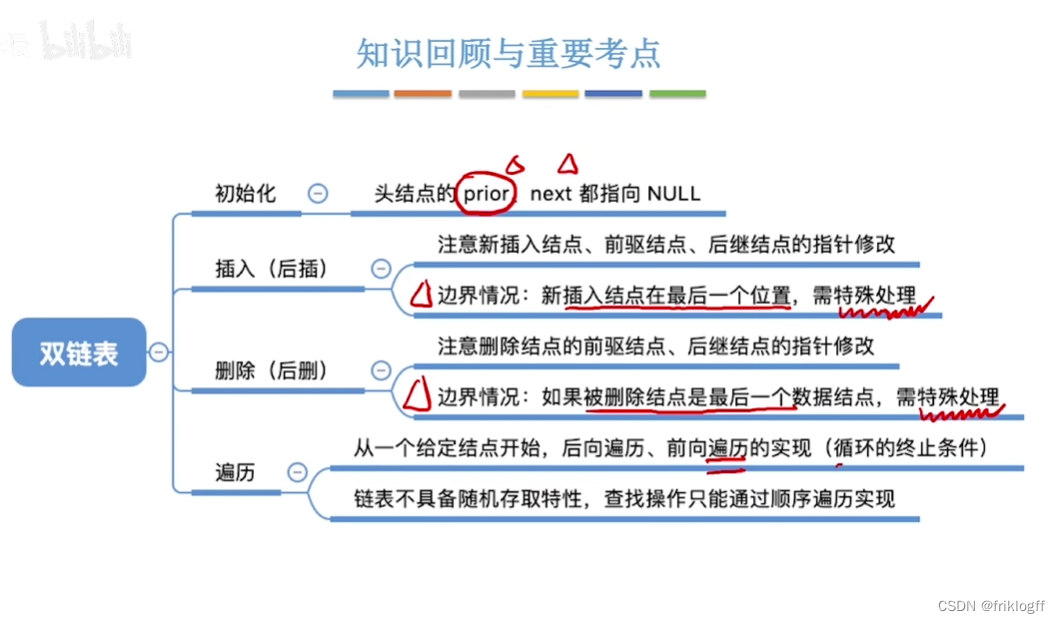
双链表
-
概念
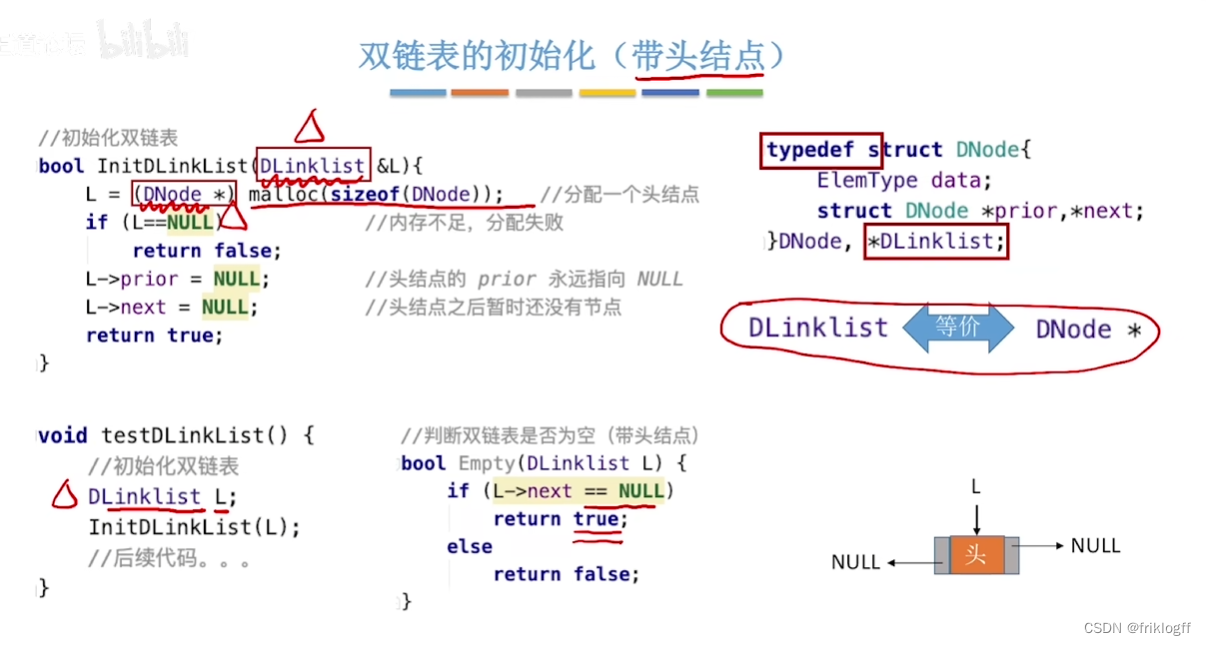
-
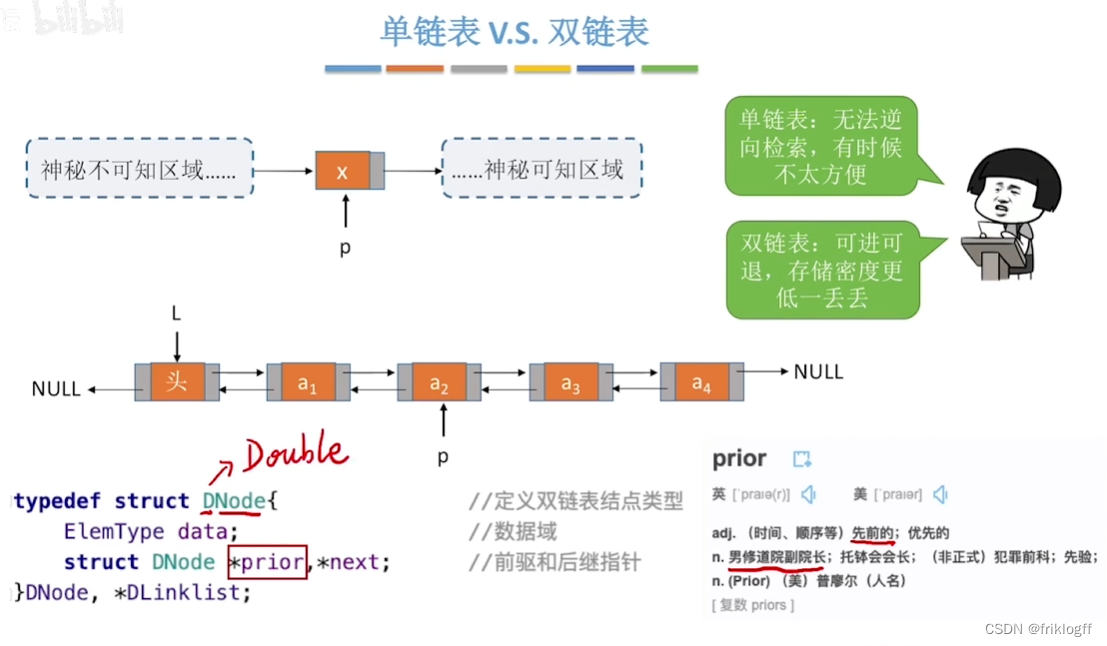
为了能快速对前驱结点操作,引入双链表。双链表结点中有两个指针priot与next,分别指向其前驱结点和后继结点
-
typedef struct DNode{ElemType data;struct DNode *prior, *next;}DNode, *DLinklist
-
-
-
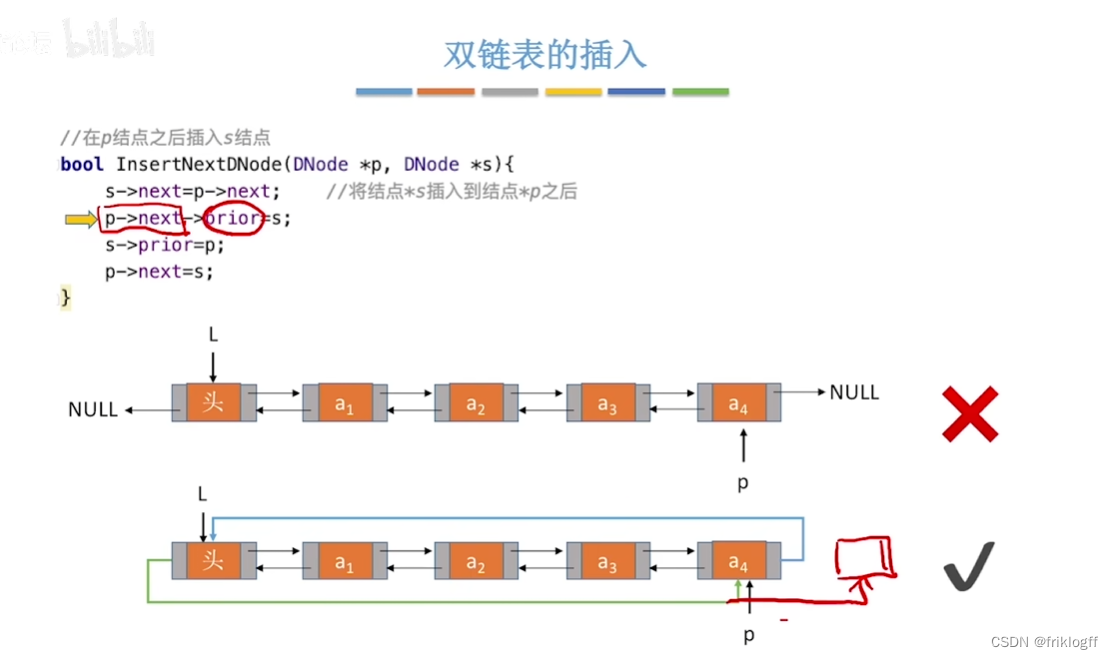
插入操作
-
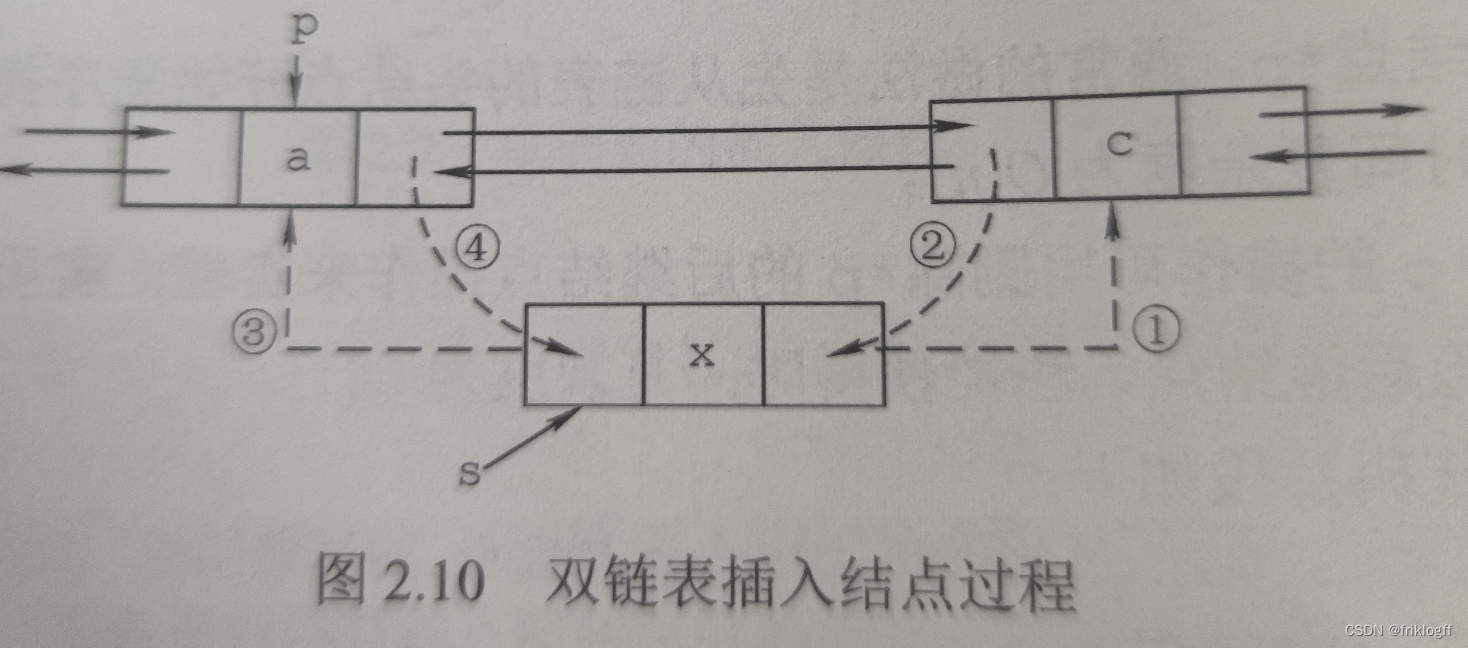
-
s->next=p->next; //将结点*s插入到结点*p之后p->next->prior=s;s->prior=p;p->next=s;
-
-
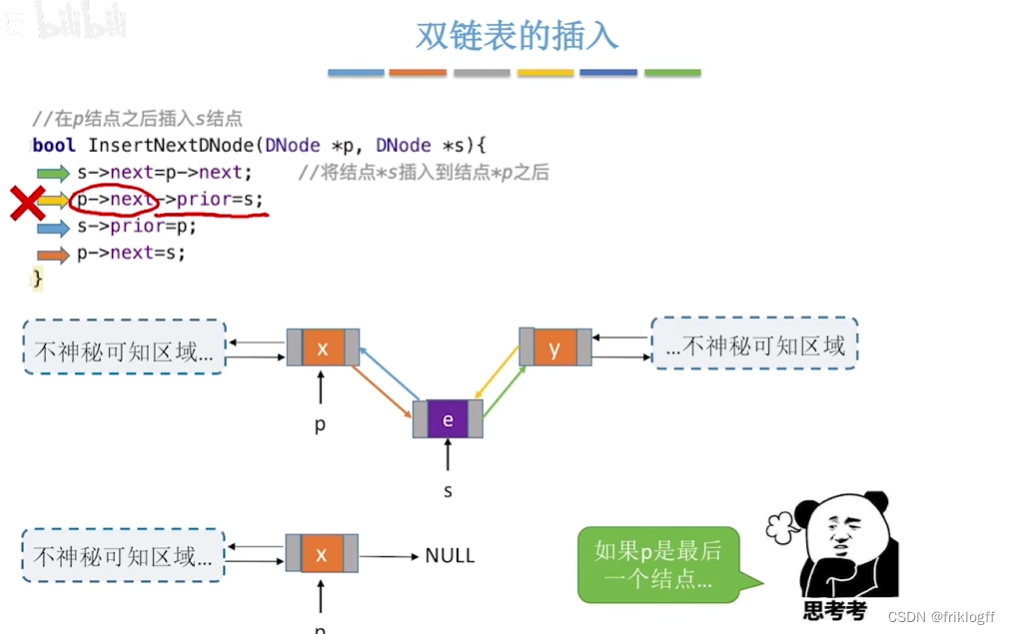
- 链表的操作原则是,确保不会造成断链和结点丢失
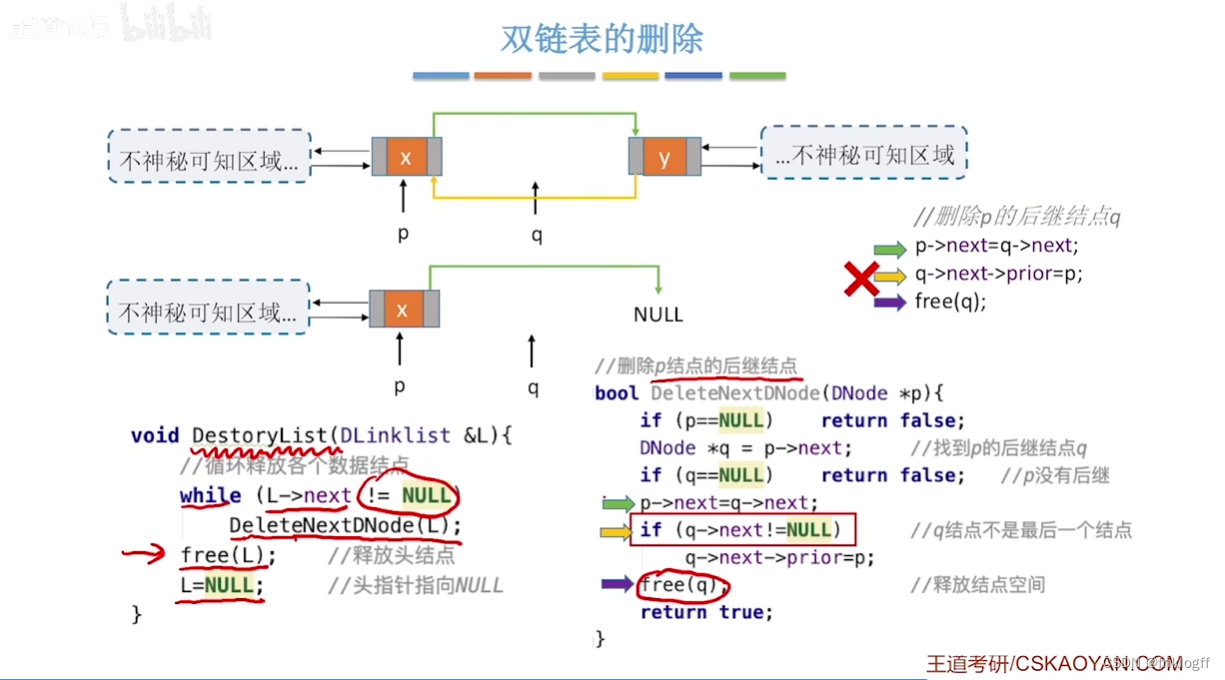
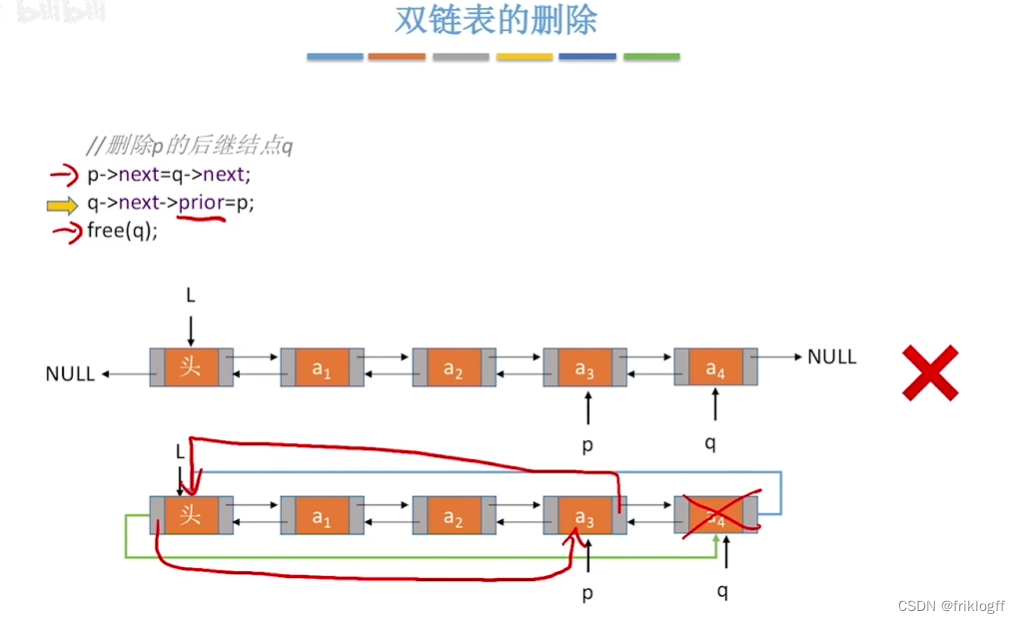
- 删除操作
-
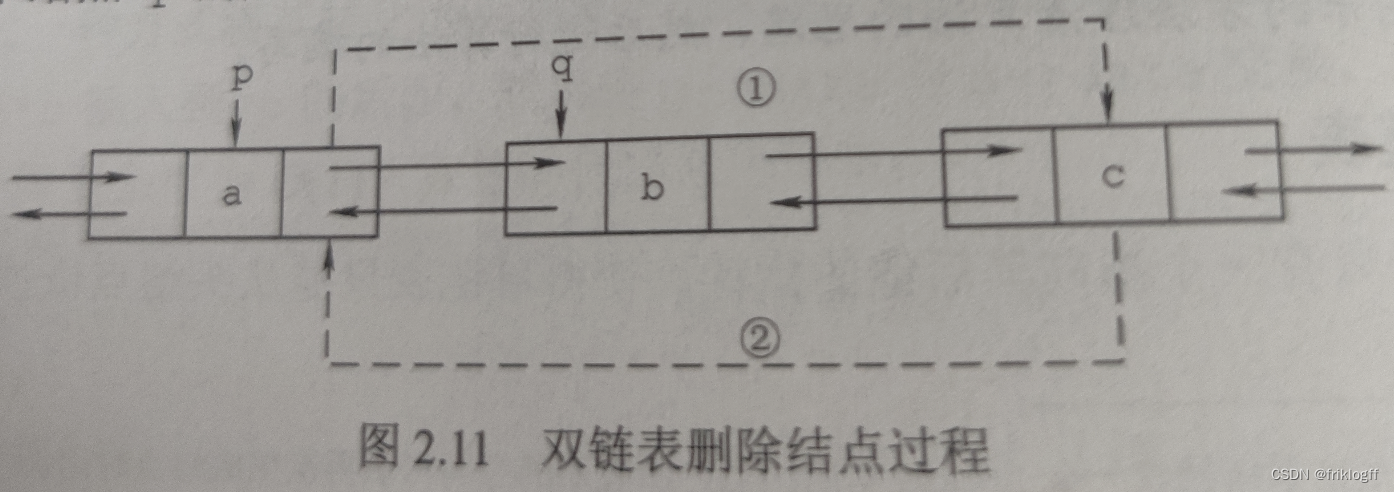
-
p->next=q->next;q->next->prior=p;free(q);
-
-
- 遍历操作
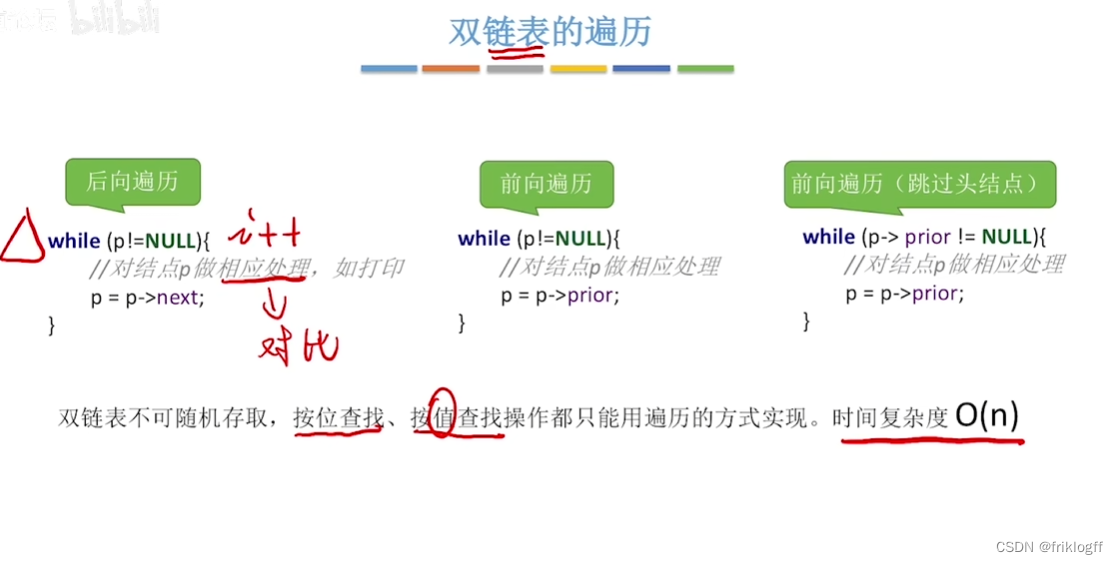
小结
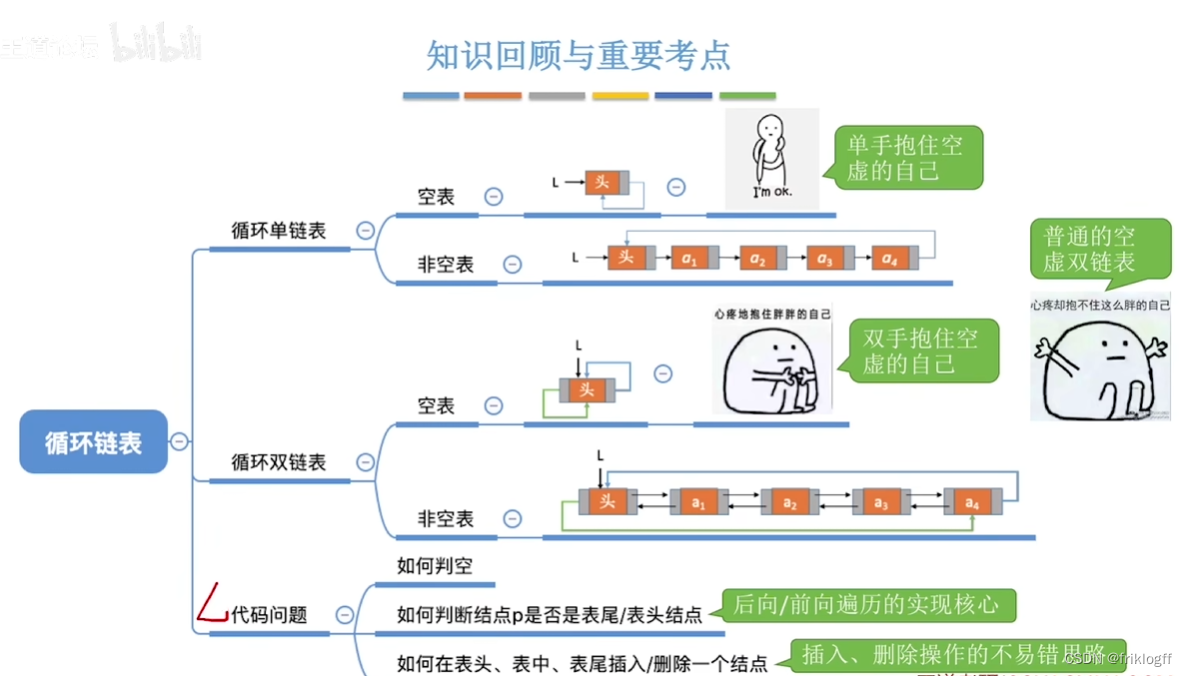
循环链表
-
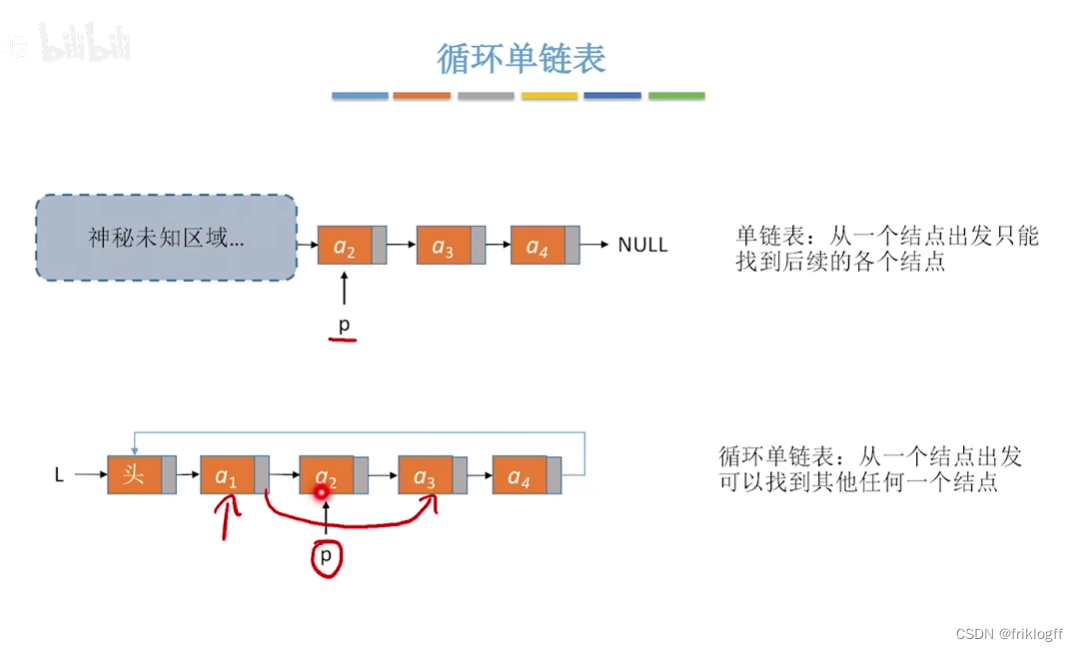
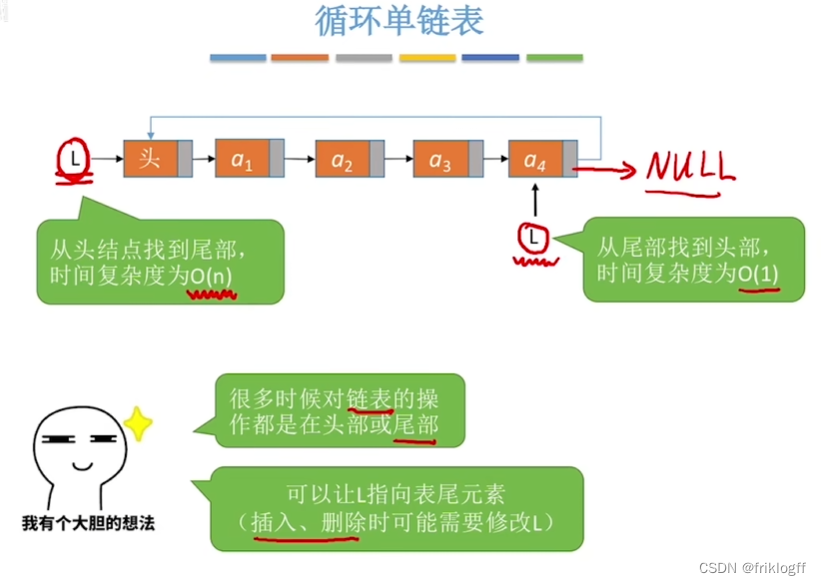
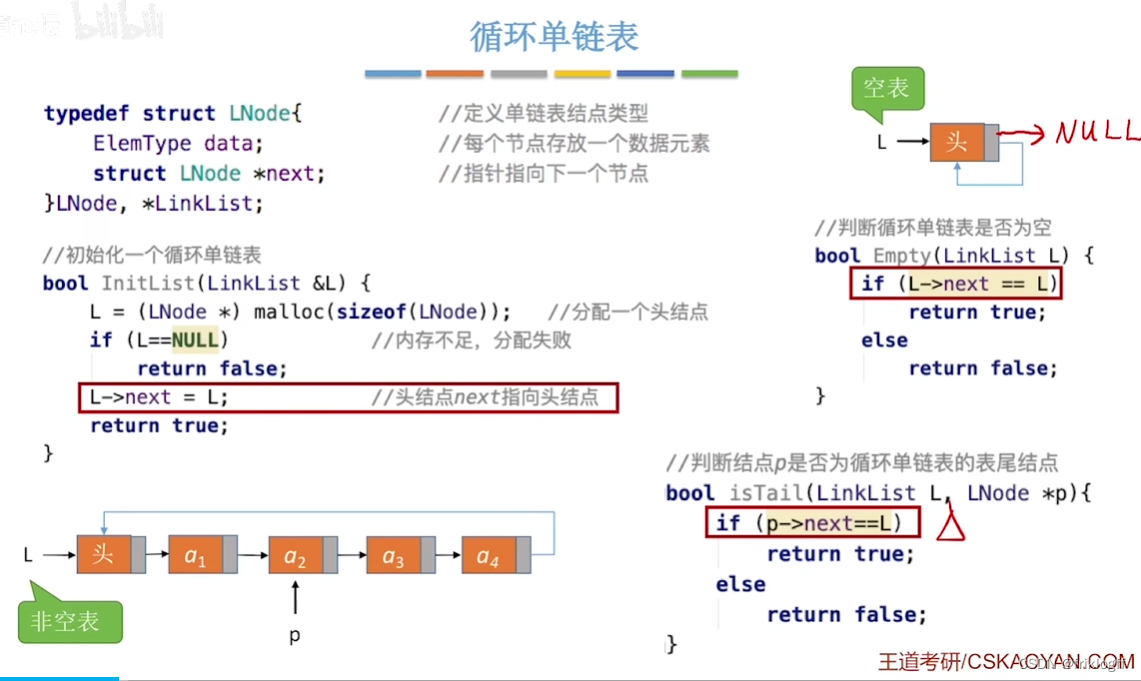
循环单链表
-

-
概念
- 与单链表区别:表中最后一个结点的指针不是NULL,而指向头结点,形成一个环
-
判空条件
- 头结点的指针是否等于头指针
-
注意:循环单链表一般不设头指针,只设尾指针R(王道讲课似乎都是头指针)
-
-
-
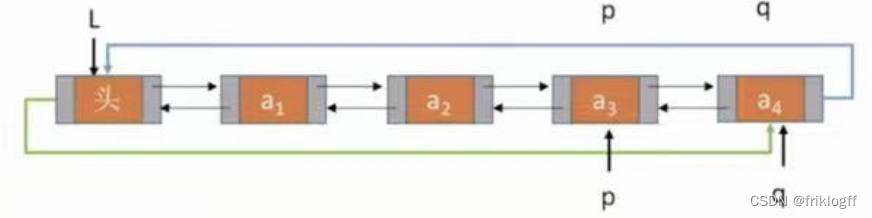
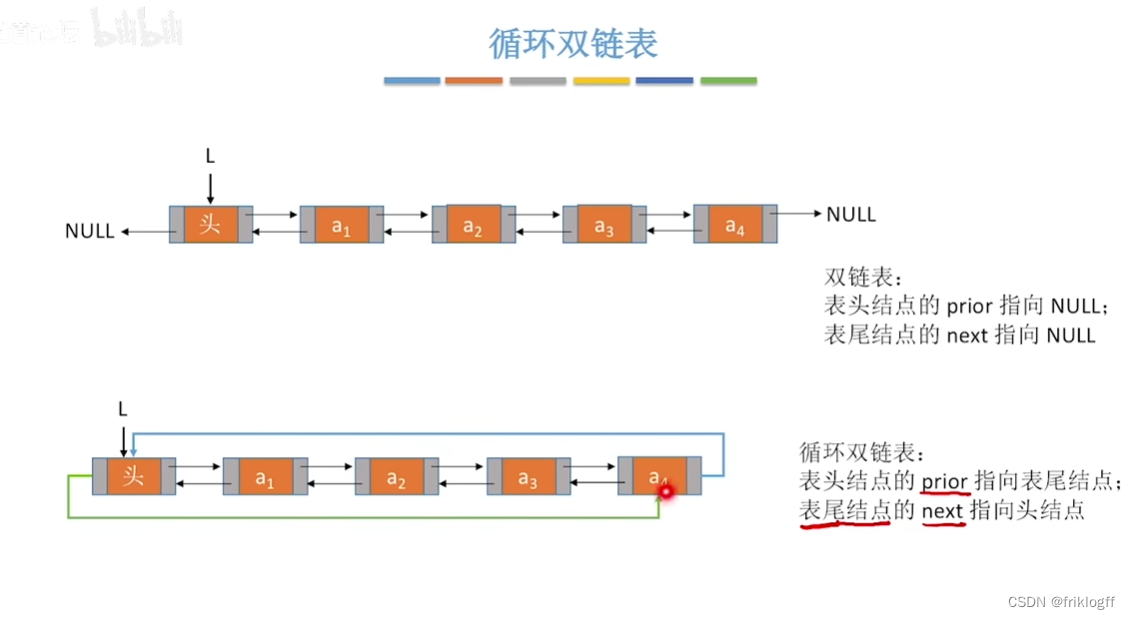
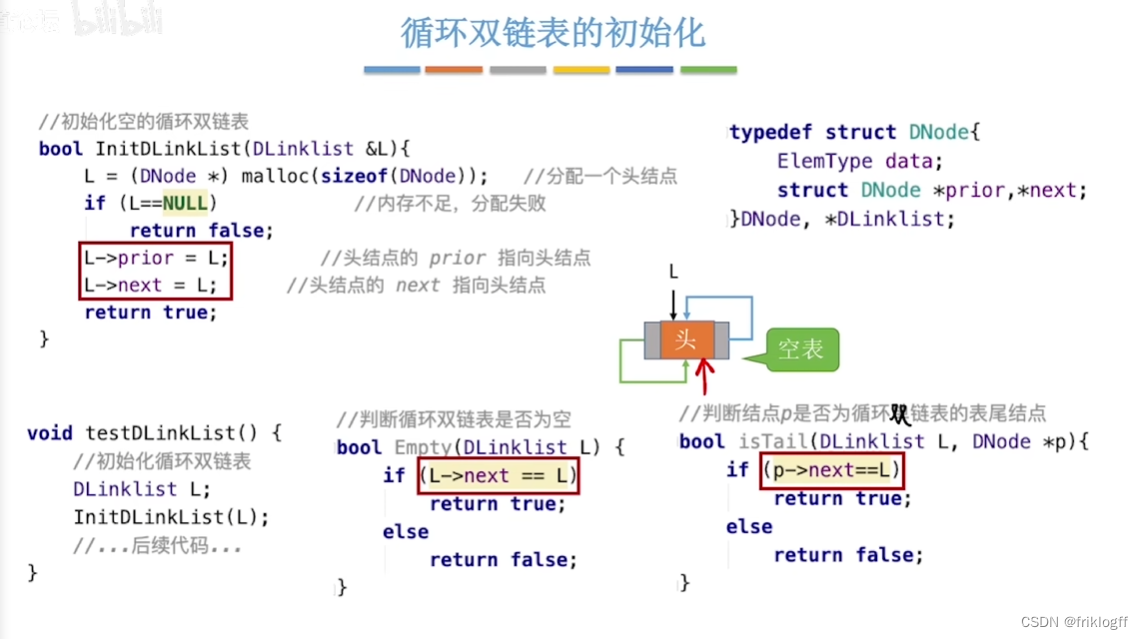
循环双链表
-
-
概念
- 与循环单链表区别:头结点的prior指针还要指向表尾结点
-
判空条件
- 当循环双链表为空时,头结点的prior域和next域都等于L
-
-
小结
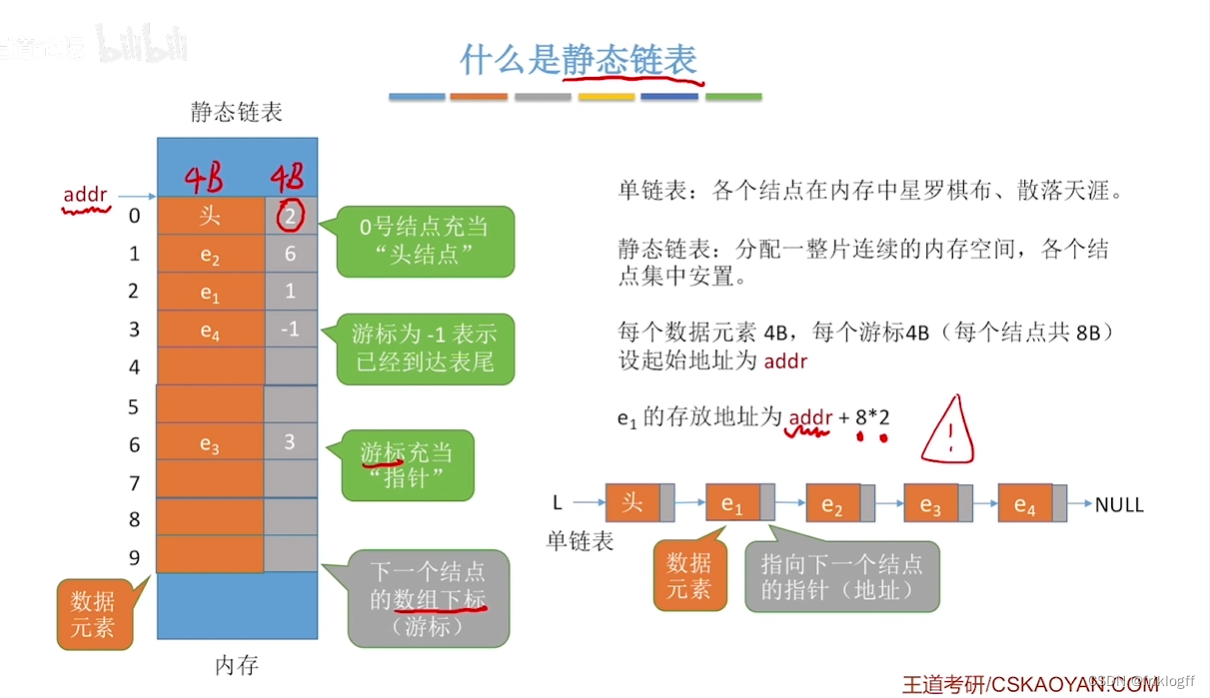
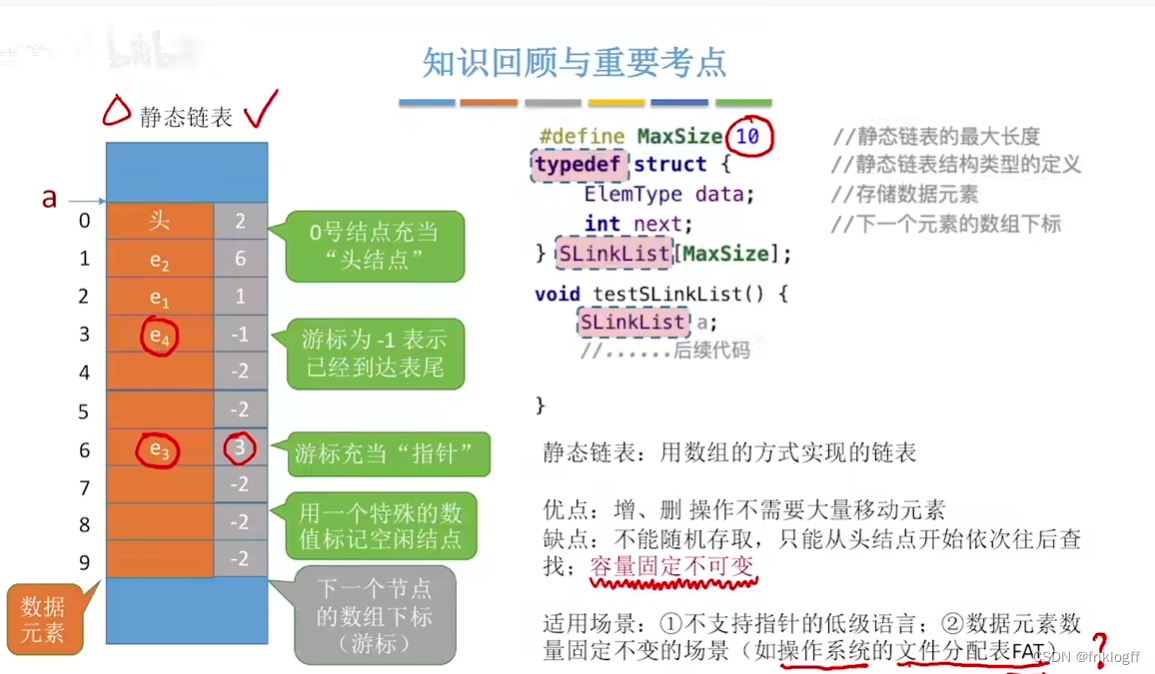
静态链表
-
-
概念
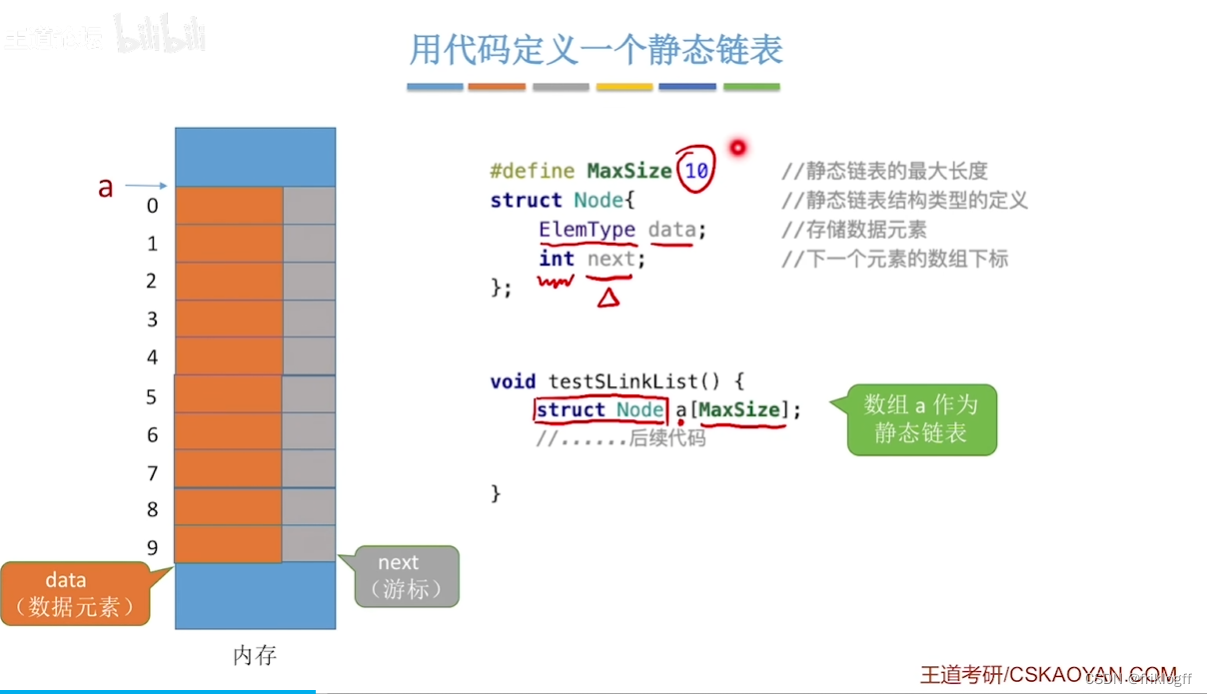
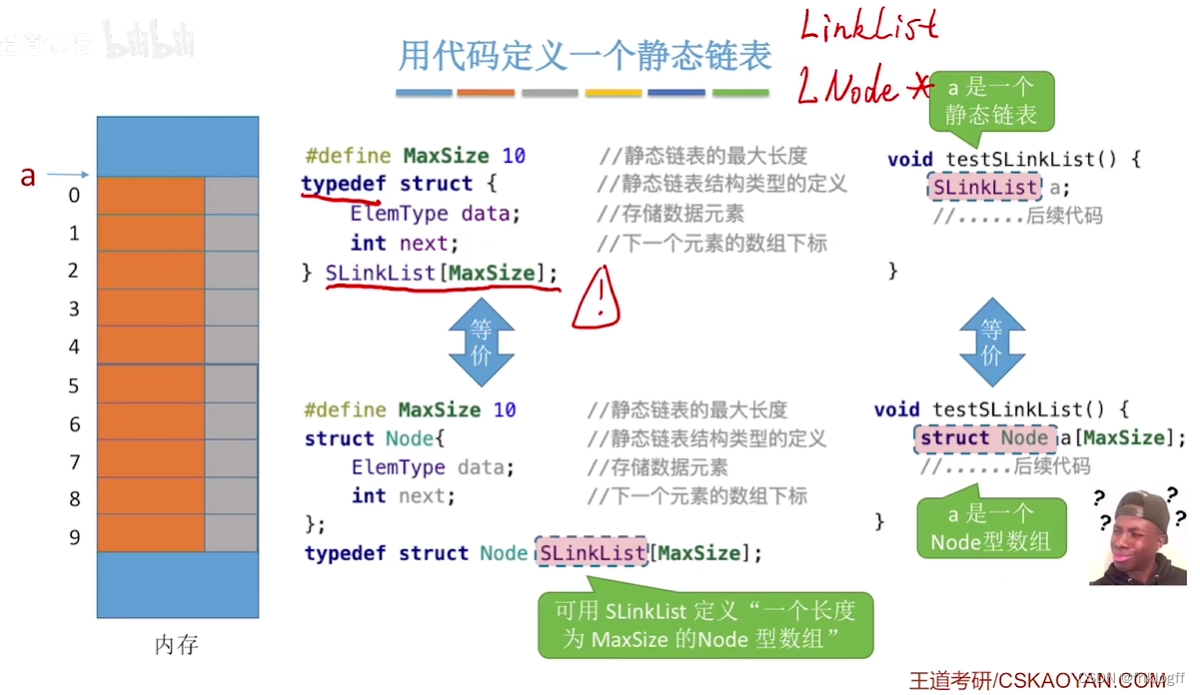
- 静态链表借助数组来描述线性表的链式存储结构,结点也有数据域和指针域,其指针是结点的相对地址(数组下标,又称游标)
-
特点
- 需要预先分配一块连续内存空间(容量固定不变)、插入删除无需移动元素、不能随机存取
-
适用场景
- 不支持指针的低级语言、数据元素数量固定不变的场景(如操作系统的文件分配表FAT)
- 不支持指针的低级语言、数据元素数量固定不变的场景(如操作系统的文件分配表FAT)
-

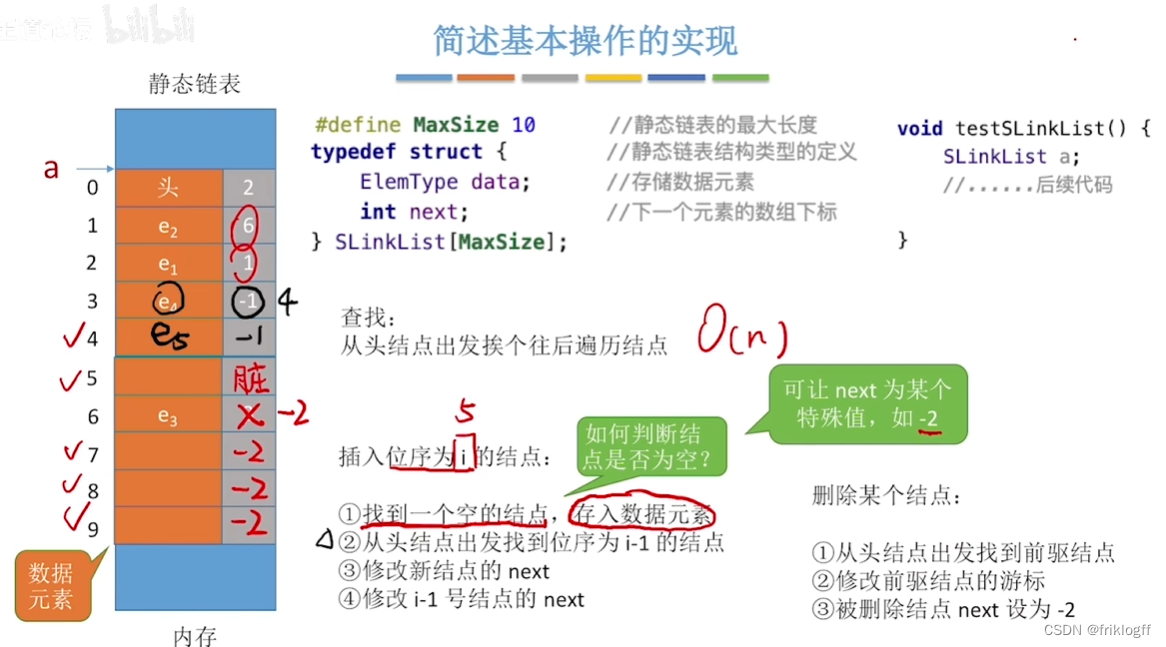
小结
顺序表V.S.链表
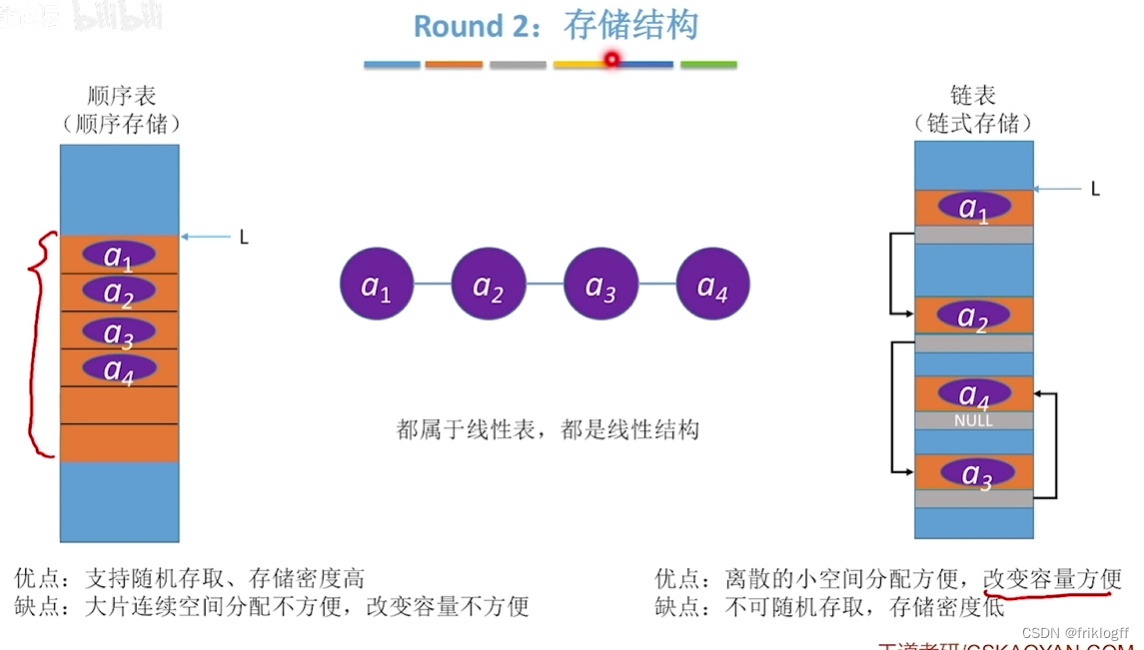
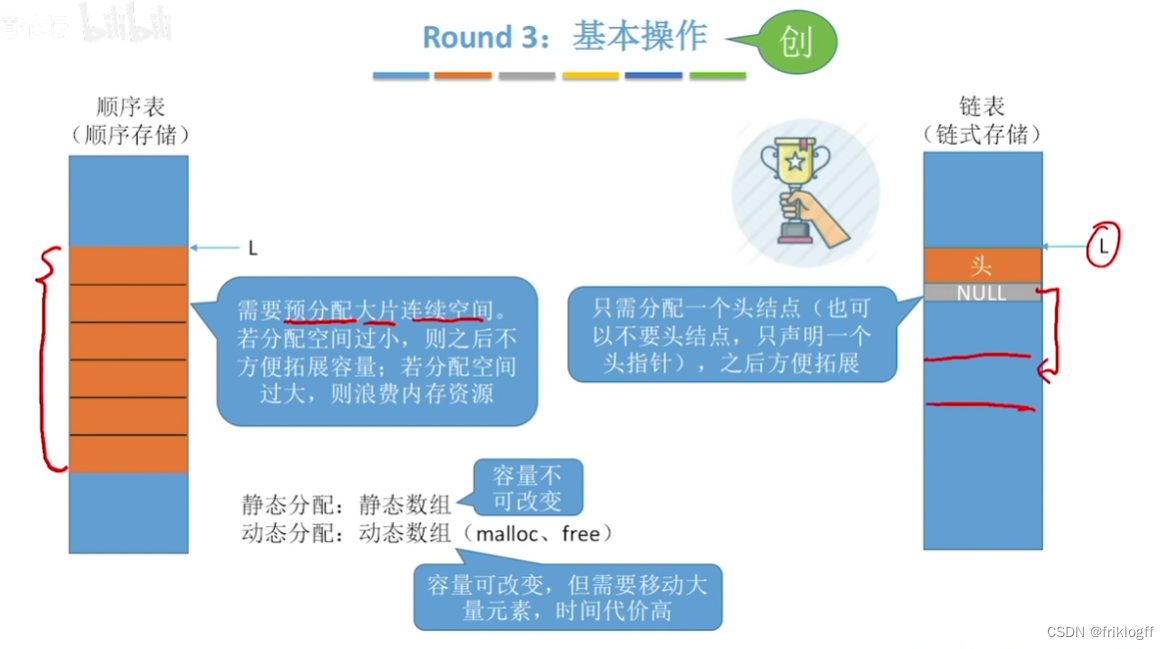
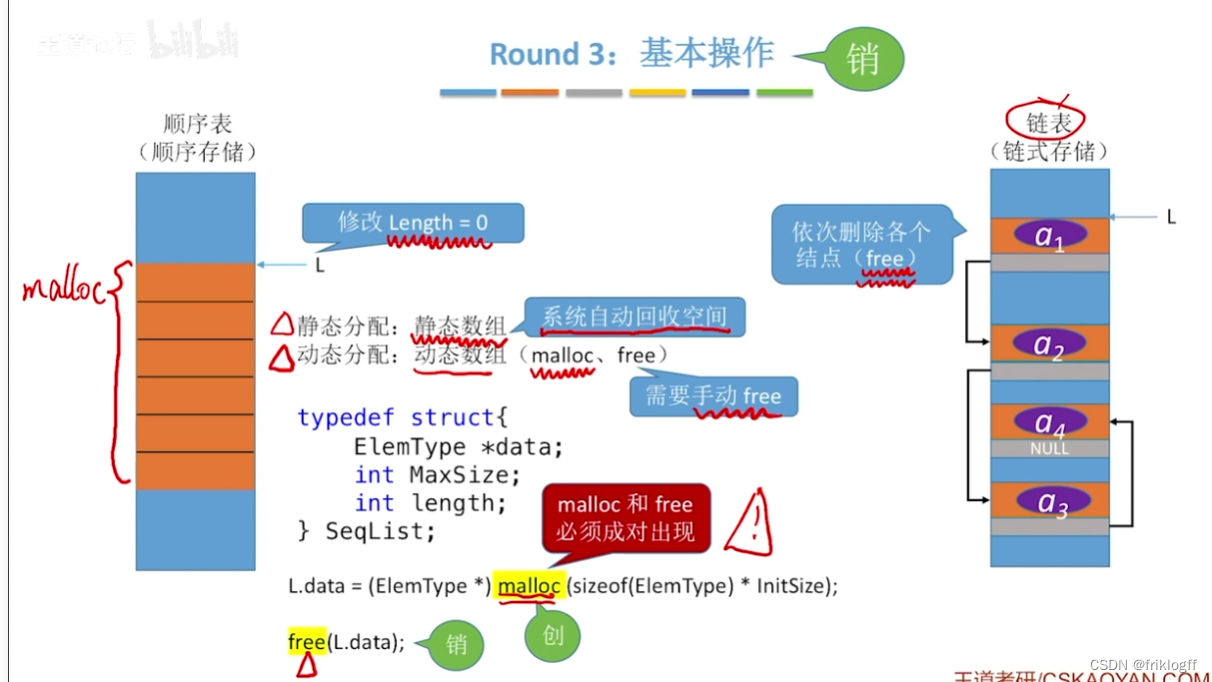
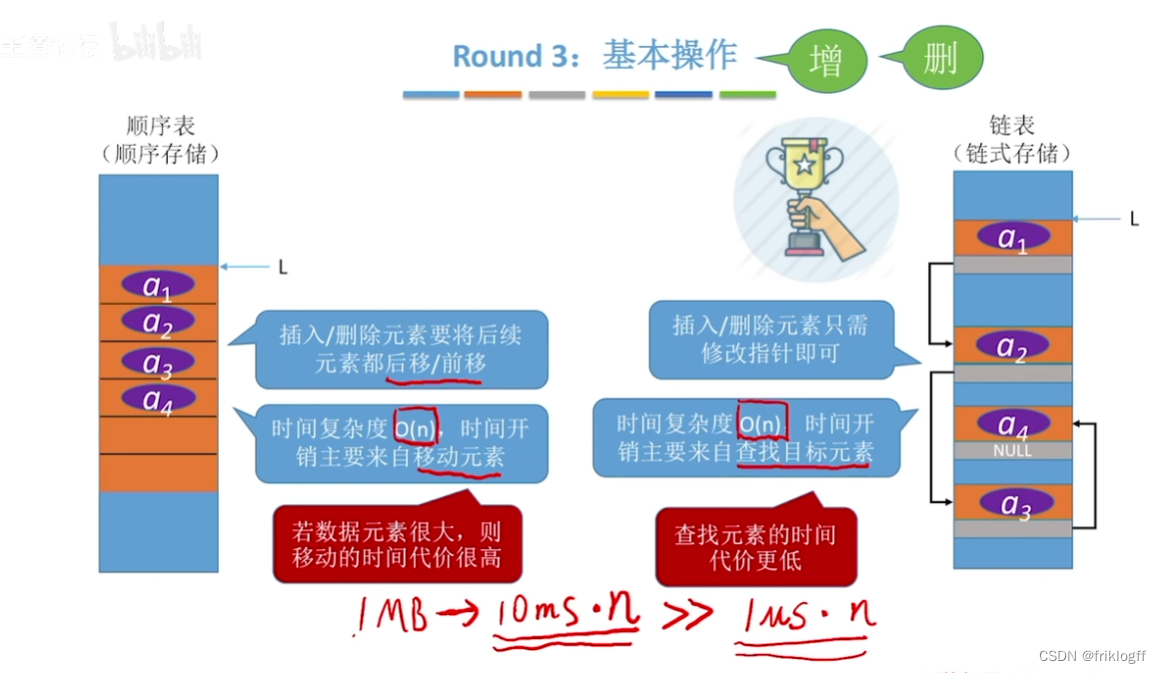
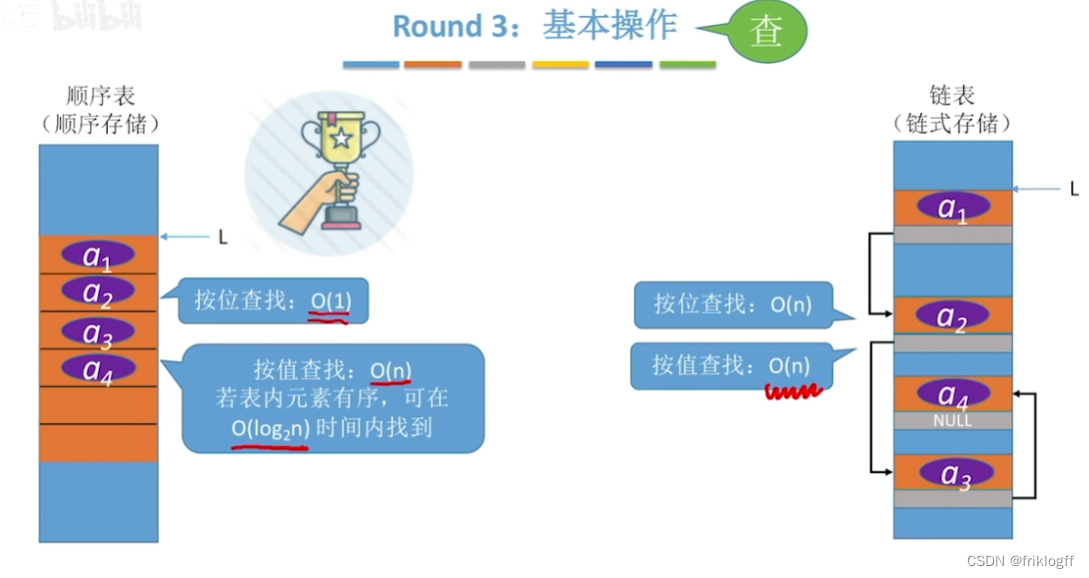


不同链表的时间效率比较
| 序号 | 链表类型 | 查找表头结点时间复杂度 | 查找表尾结点时间复杂度 | 查找结点*P的前驱结点时间复杂度 |
|---|---|---|---|---|
| 1 | 带头结点的单链表L | L->next,时间复杂度O(1) | 从L->next依次向后遍历,时间复杂度O(n) | 通过p->next无法找到其前驱(双指针可以) |
| 2 | 带头结点仅设头指针L的循环单链表 | L->next,时间复杂度O(1) | 从L->next依次向后遍历,时间复杂度O(n) | 通过p->next可以找到其前驱,时间复杂度O(n) |
| 3 | 带头结点仅设尾指针R的循环单链表 | R->next,时间复杂度O(1) | R,时间复杂度O(1) | 通过p->next可以找到其前驱,时间复杂度O(n) |
| 4 | 带头结点的双向循环链表L | L->next,时间复杂度O(1) | L->prior,时间复杂度O(1) | p->prior,时间复杂度O(1) |
顺序表和链表的比较
| 比较项目/存储结构 | 顺序表 | 链表 |
|---|---|---|
| 存储空间 | 预先分配,会导致空间闲置或溢出 | 动态分配,不会出现闲置或溢出现象 |
| 存储密度 | 不用为表示结点间的逻辑关系而增加额外存储开销 | 需要借助指针体现元素间逻辑关系,存储密度小于1 |
| 存取元素 | 随机存取,按位置访问元素时间为O(1) | 顺序存取,按位置访问元素复杂度为O(n) |
| 插入、删除 | 平均移动约表中一半元素,时间复杂度O(n) | 无需移动元素,确定位置后时间复杂度为O(1) |
| 适用情况 | 表长变化不大,且能事先确定变化范围,很少进行插入删除操作,经常按元素位置访问 | 长度变化较大,频繁进行插入或删除操作 |
补充代码
C++也可以用STL中的vector容器实现动态增长的数组
- STL是C++的标准模版库,也就是C++标准里帮我们写好了一些经常用到的东西,对于基础的数据结构,都已经给我们写好,比如写广度优先,队列的代码就可以直接用STL的queue容器,我们只要调用函数即可
随便给大家找个使用指南https://blog.csdn.net/weixin_43772166/article/details/104076670
相当于在处理算法题时候STL可以很方便帮我们完成数据结构部分,不用自己造轮子,但对于考研,如果题目就是让你实现一个循环队列,那就老老实实自己写,总之可以用但最好自己写(自己写相当于在说我很牛,你咋么敢扣分的啊),如果时间不够可以考虑用
单链表(数组模拟)
-
int v[N], l[N], idx; //初始化,分别为值、下一结点坐标、下一结点下标void init(){l[0] = -1;idx = 1;}void insert(int k, int x){ //去head,直接idx=0存头指针,使k无需-1,且消除头结点的特殊操作v[idx] = x;l[idx] = l[k];l[k] = idx++;}void delete_v(int k){l[k] = l[l[k]];}
双向链表(数组模拟)
-
int v[N], l[N], r[N], idx; //同理void init(){l[0]=-1, r[0]=1, l[1]=0, r[1]=-1; //用最开始两个结点做头尾指针idx=2;}void insertL(int k,int x){ //注意这里的三个函数,由于占用了数组前两个元素,题目给的k值需要+1v[idx] = x;l[idx] = l[k];r[idx] = k;r[l[k]] = idx;l[k] = idx++;}void insertR(int k,int x){v[idx] = x;r[idx] = r[k];l[idx] = k;l[r[k]] = idx;r[k] = idx++;}void delete_v(int k){r[l[k]] = r[k];l[r[k]] = l[k];}
考研真题
408 - 2023
(考研真题待更新)


![[AIGC] Redis基础命令集详细介绍](https://img-blog.csdnimg.cn/direct/43ef8148a08a4984886cd00b3cac1a7e.png)
