参考博客:
(1)算法数据结构——动态规划算法(Dynamic Programming)超详细总结加应用案例讲解
(2)【路径规划】全局路径规划算法——动态规划算法(含python实现)
(3)路径规划与轨迹跟踪系列算法学习_第3讲_动态规划算法
(4)全局路径规划算法-动态规划算法DP
1 动态规划简介
动态规划最早由理查德 · 贝尔曼于 1957 年在其著作「动态规划(Dynamic Programming)」一书中提出。这里的 Programming 并不是编程的意思,而是指一种「表格处理方法」,即将每一步计算的结果存储在表格中,供随后的计算查询使用。
- 动态规划是运筹学的一个分支,是求解多阶段决策过程最优化问题的数学方法
- 各个阶段决策的选取不是任意确定的,它依赖于当前面临的状态,又影响以后的发展。当各个阶段的决策确定后,就组成了一个决策序列,因而也就决定了整个过程的一条活动路线,这样的一个前后关联具有链状结构的多阶段过程就称为多阶段决策问题。
- 动态规划在车辆工程技术领域有着广泛的应用,如“两档变速器最优换挡规律”、“混合动力汽车最优能量管理策略”、“栅格地图最优路径搜索”等
2 算法思想
动态规划最优化原理:把多阶段决策问题转化为一系列单阶段最优化问题,简而言之,一个最优策略的子策略必然也是最优的
逆向寻优,正向求解。
DP本质由三个阶段组成
(1)逆向遍历每一个阶段
(2)遍历每一个阶段的每一个状态
(3)遍历当前状态所在阶段的上一阶段的每一个状态
(4)更新当前状态的到上一个阶段的状态的最短距离
(5)直到遍历完所有节点
3 动态规划
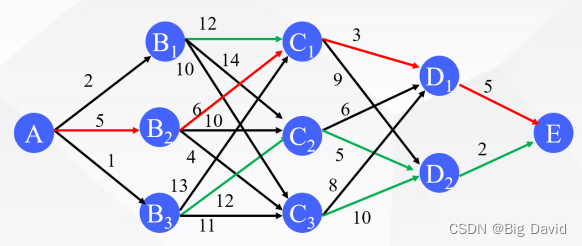
设终点为E,逆向运用DP算法
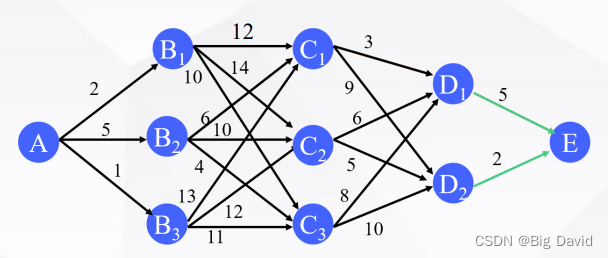
① 第四阶段(D→E): D有两条路线到终点E
f 4 ( D 1 ) = 5 f 4 ( D 2 ) = 2 f_{4}\left(D_{1}\right)=5 \quad f_{4}\left(D_{2}\right)=2 f4(D1)=5f4(D2)=2
② 第三阶段(C→D): C到D有6条路线
第3阶段的C有3个状态值,分别讨论经过该状态
值的最优路线

③ 第二阶段(B →C): B 到C有9条路线

④ 第一阶段(A→B): A到B有3条路线

Python:
INF = float('INF')
### 状态节点定义
graph = {'4': {'D1': {'E': 5}, 'D2': {'E': 2}},'3': {'C1': {'D1': 3, 'D2': 9}, 'C2': {'D1': 6, 'D2': 5}, 'C3': {'D1': 8, 'D2': 10}},'2': {'B1': {'C1': 12, 'C2': 14, 'C3': 10}, 'B2': {'C1': 6, 'C2': 10, 'C3': 4}, 'B3': {'C1': 13, 'C2': 12, 'C3': 11}},'1': {'A': {'B1': 2, 'B2': 5, 'B3': 1}}}
### 最优路径及其距离值定义
INF = float('INF')
# 初始时距离为无穷大
dists = {'A': INF,'B1': INF,'B2': INF,'B3': INF,'C1': INF,'C2': INF,'C3': INF,'D1': INF,'D2': INF,'E': 0}path_opt = {'A': ['A'],'B1': ['B1'],'B2': ['B2'],'B3': ['B3'],'C1': ['C1'],'C2': ['C2'],'C3': ['C3'],'D1': ['D1'],'D2': ['D2'],'E': ['E']
}# 每一个节点的父节点
parents = {'A': None,'B1': None,'B2': None,'B3': None,'C1': None,'C2': None,'C3': None,'D1': None,'D2': None,'E': None}# 动态规划函数
def DP(graph, dists, parents):# 逆向遍历每一个阶段for period_key in graph.keys():# 遍历每个阶段的每一个状态节点for key_i in graph[period_key].keys(): min_key = None# 遍历当前阶段的每个状态节点到下一阶段的每一条路径for key_i_dist in graph[period_key][key_i].keys(): if graph[period_key][key_i][key_i_dist] + dists[key_i_dist] < dists[key_i]:dists[key_i] = graph[period_key][key_i][key_i_dist] + dists[key_i_dist]parents[key_i] = key_i_dist# 找出最小距离值的节点min_key = key_i_dist# 将最小距离值的节点添加到最优路径集合path_opt[key_i].extend(path_opt[min_key]) DP(graph, dists, parents)
print("E到每个节点的最短距离:\n",dists)
print("====================")
print("最优时每个节点的父节点:\n",parents)
print("====================")
print("最优路径:\n",path_opt)
E到每个节点的最短距离:{'A': 19, 'B1': 20, 'B2': 14, 'B3': 19, 'C1': 8, 'C2': 7, 'C3': 12, 'D1': 5, 'D2': 2, 'E': 0}
====================
最优时每个节点的父节点:{'A': 'B2', 'B1': 'C1', 'B2': 'C1', 'B3': 'C2', 'C1': 'D1', 'C2': 'D2', 'C3': 'D2', 'D1': 'E', 'D2': 'E', 'E': None}
====================
最优路径:{'A': ['A', 'B2', 'C1', 'D1', 'E'], 'B1': ['B1', 'C1', 'D1', 'E'], 'B2': ['B2', 'C1', 'D1', 'E'], 'B3': ['B3', 'C2', 'D2', 'E'], 'C1': ['C1', 'D1', 'E'], 'C2': ['C2', 'D2', 'E'], 'C3': ['C3', 'D2', 'E'], 'D1': ['D1', 'E'], 'D2': ['D2', 'E'], 'E': ['E']}
Matlab(参考Ally)
clc
clear
close all%% 阶段-状态定义
stages = 5;
nodes_dist = cell(stages-1,3);% 第1阶段
nodes_dist{1,1} = 1;
nodes_dist{1,2} = [1,2,3];
nodes_dist{1,3} = [2,5,1];% 第2阶段
nodes_dist{2,1} = [1;2;3];
nodes_dist{2,2} = [1,2,3];
nodes_dist{2,3} = [12, 14, 10; 6, 10, 4; 13, 12, 11];% 第3阶段
nodes_dist{3,1} = [1;2;3];
nodes_dist{3,2} = [1,2];
nodes_dist{3,3} = [3, 9; 6, 5; 8, 10];% 第4阶段
nodes_dist{4,1} = [1;2];
nodes_dist{4,2} = 1;
nodes_dist{4,3} = [5; 2];% 第4阶段
nodes_dist{5,1} = 1;
nodes_dist{5,2} = 1;
nodes_dist{5,3} = 0;% 最优路径及其距离值定义
path = cell(stages, 1);
dist = cell(stages, 1);
for i = 1:stages-1dist{i, 1} = nodes_dist{i,1};dist{i, 2} = inf(length(dist{i, 1}), 1);path{i, 1} = nodes_dist{i,1};
end
dist{stages, 1} = 1;
dist{stages, 2} = 0;
path{stages, 1} = 1;
path{stages, 2} = 1;
% 根据最后一个阶段,直接初始化%% 逆向寻优% 第一层循环:逆向遍历每一个阶段
for i = stages-1:-1:1num_states_f = length(nodes_dist{i, 1}); % 第二层循环:遍历第i阶段的每一个状态for j = 1:num_states_fnum_states_r = length(nodes_dist{i+1, 1}); % 第三层循环:遍历第i阶段的第j个状态到第i+1阶段的每一条路径for k = 1:num_states_rif nodes_dist{i,3}(j,k) + dist{i+1,2}(k,1) < dist{i,2}(j,1)dist{i,2}(j,1) = nodes_dist{i,3}(j,k) + dist{i+1,2}(k,1);path{i, 2}(j,:) = [j, path{i+1, 2}(k,:)];endendend
end%% 正向求解
path_opt = path(1,:);
dist_opt = dist{1,2};