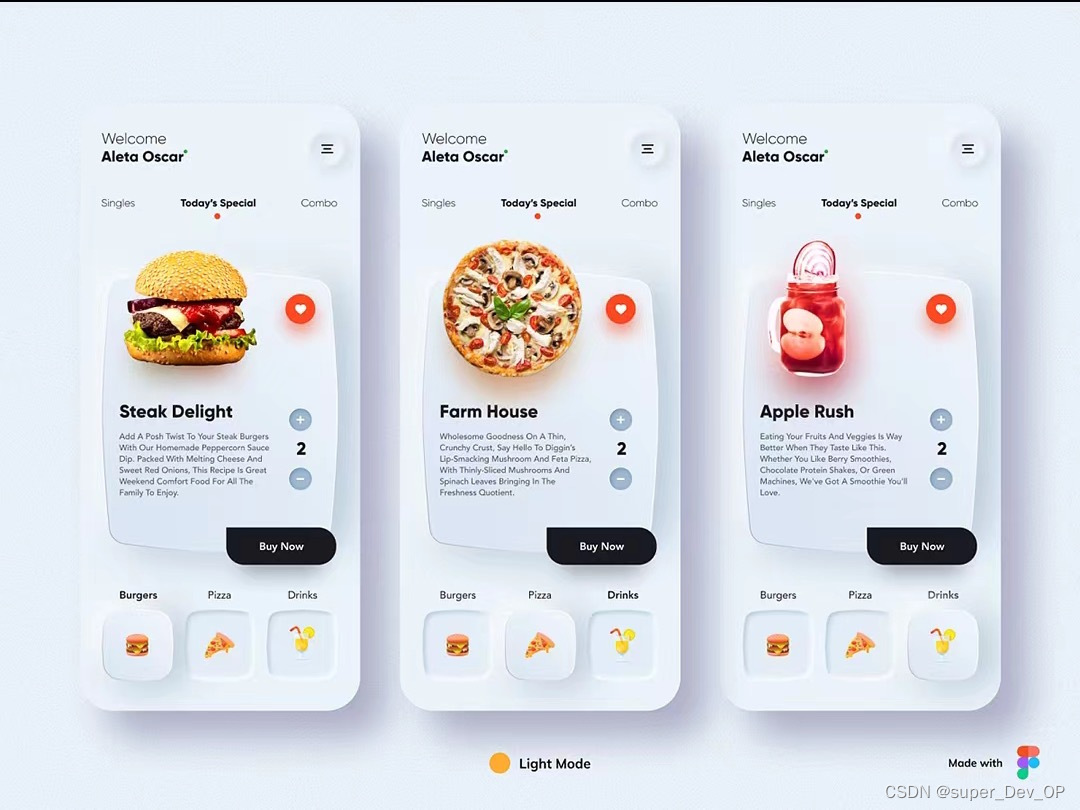
紧接着上一篇幅,点火条件的图形表示如下。
利用单位阶跃函数可表示点火的式子:y=u(w1x1+w2x2+w3x3-θ)

因为u表示的是单位阶跃函数,那么一般化点火的式子可以表示为:y=a(w1x1+w2x2+w3x3-θ),此处的a表示激活函数,x1、x2、x3 是模型允许的任意数值,与上面不同的是,抛出了生物的限制,y 是函数 a 能取到的任意数值,不止于取0或1,这里涉及到了神经元与神经单元的不同。
神经元是基于生物上的,而神经单元是我们抽象化、简化后的神经元数学模型。其不同如下:

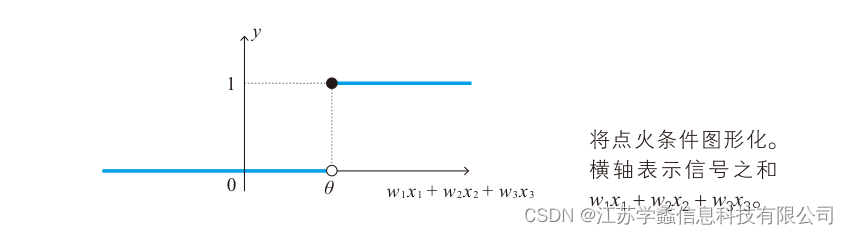
激活函数Sigmoid 函数 σ(z)的表达式
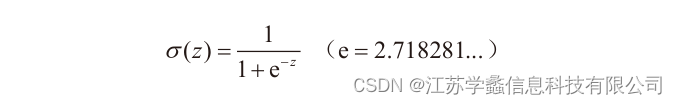
对式子y=a(w1x1+w2x2+w3x3-θ)再进行优化:y=a(w1x1+w2x2+w3x3+b),其中b称为偏置,加权输入z=w1x1+w2x2+w3x3+b。
加权输入z可以看作是两个向量的内积(内积是对应位置的数值相乘再相加即可),则z=(w1,w2,w3,b)(x1,x2,x3,1)
神经网络
将神经元的工作在数学上抽象化,并以其为单位人工地形成网络,这样的人工网络就是神经网络。简单的说,就是神经单元连接而成的网络就是神经网络。
神经网络可以分为三层,各层称为输入层、隐藏层、输出层,其中隐藏层称为中间层。各层分别执行特定的信号处理操作。
- 输入层负责读取给予神经网络的信息。属于这个层的神经单元没有输入箭头,它们是简单的神经单元,只是将从数据得到的值原样输出。
- 隐藏层的神经单元执行加权输入z和输出y的处理操作。在神经网络中,这是实际处理信息的部分。
- 输出层与隐藏层一样执行信息处理操作,并显示神经网络计算出的结果,也就是整个神经网络的输出。
例题

解答如下
前一层的神经单元与下一层的所有神经单元都有箭头连接,这样的层构造称为全连接层。

![[云原生] K8S声明式资源管理](https://img-blog.csdnimg.cn/direct/06b922e839a748c7b189047639cc07c9.png)