R-B Tree
- 简介
- 特性
- B树
- 特性
- m阶B树的性质(这些性质是B树规定的)
- B树的搜索
- B树的添加
- B树的删除——非叶子结点
简介
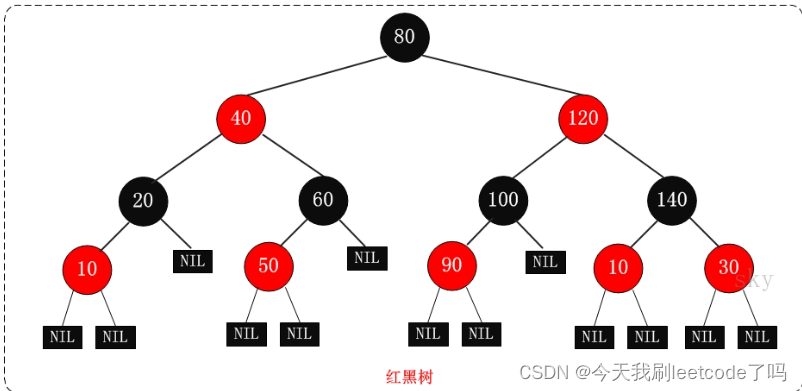
R-B Tree又称为Red-Black Tree,红黑树。是一种特殊的二叉查找树,红黑树的每个节点上都有存储为表示结点的颜色,可以是红或者黑色。
特性
- 每个结点或者是黑色或者红色
- 根结点是黑色
- 每个叶子节点是黑色(这里的叶子结点指的是:NULL的叶子结点——外部节点 (写代码时候不用加入这些结点))
- 如果一个节点红色的,则它的子结点黑色的
- 结点红色的,则它的父结点黑色的(否则:如果父结点是红色,那么不满足上一条性质 如果该节点是红色的,那么它的子结点是黑色的这个性质了)
- 从根结点到叶子结点(外部节点)的所有路径上不能包含两个连续的红结点
- 从任意节点到叶子结点的所有路径都包含相同数量的黑节点
特性5说明:确保没有一条路径会比其他路径长出俩倍。因而,红黑树是相对是接近平衡的二叉树。
这样使得在叶子结点中原来的度为0或者度为1的结点最后全部变成了度为2的结点
B树
B树是一种平衡的多路搜索树
特性
- B树的一个节点可以存储超过两个元素,可以拥有超过两个子结点
- 平衡,每个结点的所有子树高度一致
- B树 比较矮
m阶B树的性质(这些性质是B树规定的)
可以理解为一个节点最多拥有的子结点数目(3阶B树:代表一个结点最多含有3个子结点)
m阶B树:代表一个结点最多包含5个子结点
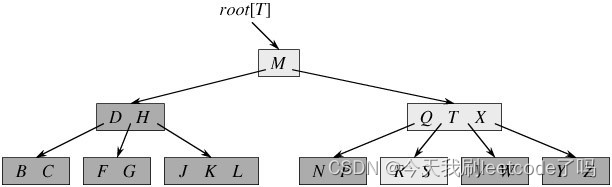
下图所示的B树:最多的结点是(包含元素QTX结点,最多包含了4个结点——称为4阶B树)
前提:假设一个节点存储的元素个数为X,
- 那么其根结点:1≤X≤m-1(当X=m-1时候才会存在m个根结点)
- 那么对于非根结点:┌m/2┐-1≤X≤m-1()
- 一个节点它的子结点的个数等于这个结点的元素个数+1:子结点的个数为y=x+1
4 那么非根结点的个数:为非根结点的元素左右加一:┌m/2┐≤y≤m
例如:8阶B树,其子结点的个数≤8, m=8, ┌m/2┐ = 4, 4≤y≤8, 3≤X≤7,则8阶B树可以称为(4,8)树;4-8树- 非根结点:┌m/2┐(┌m┐表示对m向上取整)-1≤X≤m-1
思考为什么非根结点必须满足┌m/2┐-1的向上取整的性质
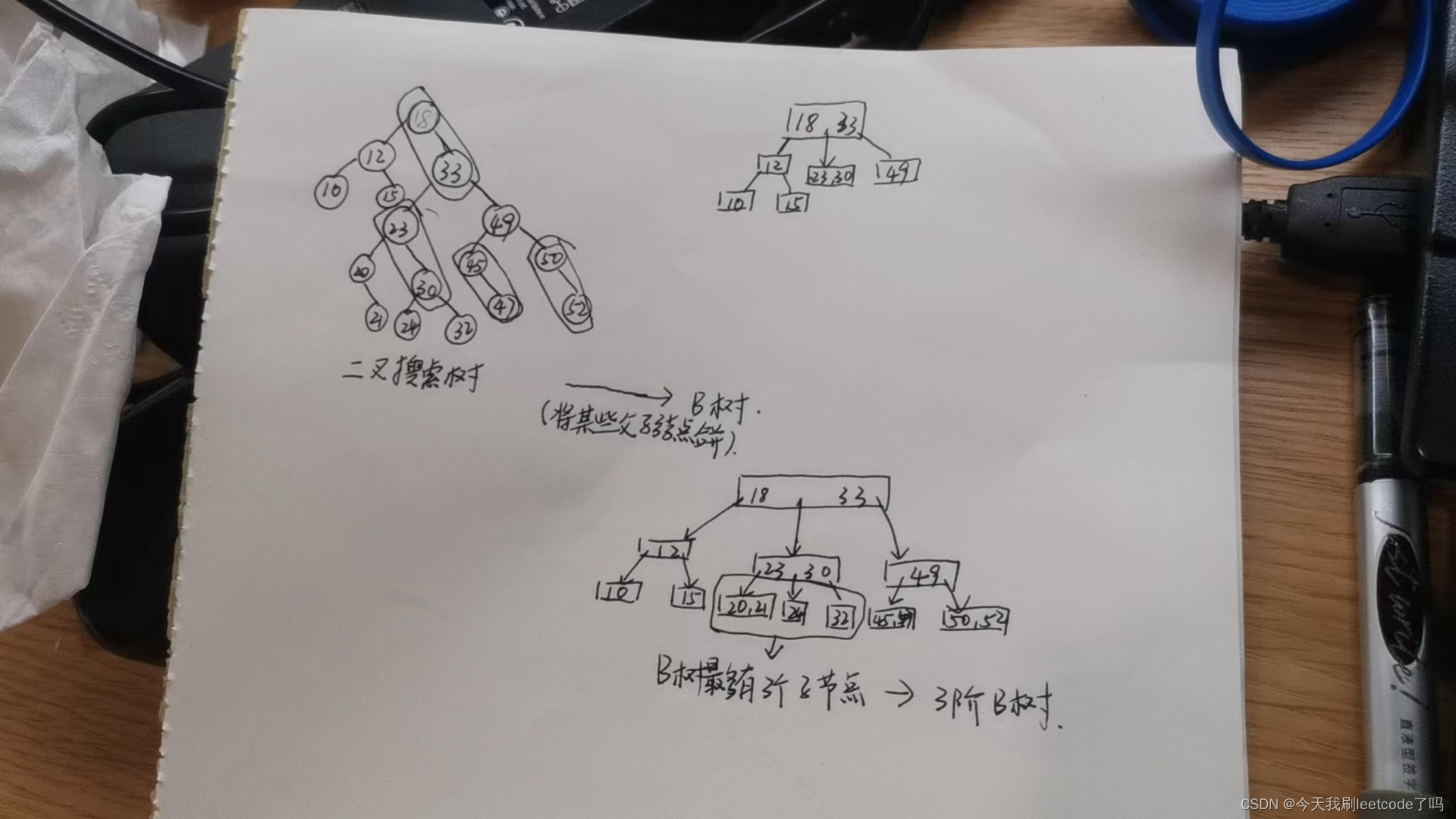
B树与二叉搜索树具有等价性:
二叉搜索树的多代结点合并可以获得一个超级结点(存储多个元素)
两代合并的超级结点首先满足如果根结点存在子结点,那么子结点的数目是根结点的数目+1===>y = x+1最多含有四个子结点
三代合并的超级结点(那么合并的超级结点 其存在的元素个数最多是将3代中的七个结点 合并在一个结点中,最终形成了具有7个元素的超级结点,那么最终其子节点的个数最多有8个(8阶B树))
n代合并的超级结点,那么最多含有2n个子结点也就是2n阶树可以理解为n代的子结点的最多个数
m阶B树,最多需要log2m代进行合并
B树的搜索
此图呈现的是4阶B树
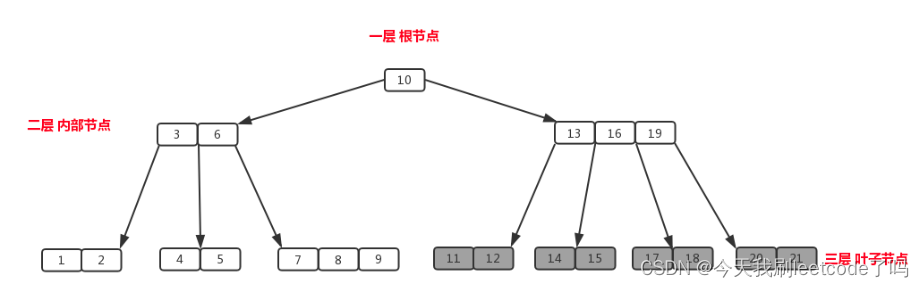
B树的搜索流程:
- 先在结点内部通过从小到大顺序来搜索元素
- 如果命中,搜索结束
- 如果未命中,再通过去对应的子结点中搜索元素,重复步骤1的操作。
B树的添加
明确:新添加的元素必定是添加到叶子结点(不断比较,直到到最后一层,进行结点的添加)
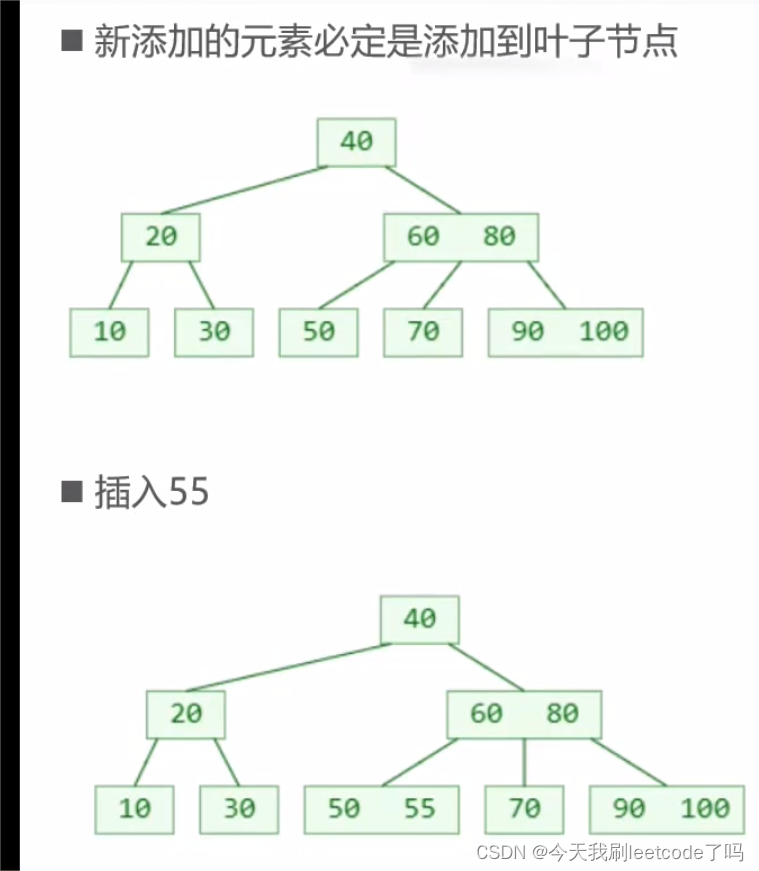
如果这个B树是3阶B树——>结点最多存储2个元素,此时如果插入98到右下角的子结点以后,出现上溢(overflow)
上溢结点的元素个数必然等于B树的阶数
求出上溢结点最中间元素的位置为K,将K位置的元素与父结点合并,再将K位置的元素向上与父结点合并
将[0,k-1]以及[k1,m-1]的位置的元素分裂成两个子结点
这两个子结点的元素的个数,必然都不会低于最低限制(┌m/2┐-1)
一次分裂完毕后,可能导致父结点上溢,依然按照上述方式解决。
最极端的情况可能是一直分裂到根结点。
B树的删除——非叶子结点
假如需要删除的元素在非叶子节点中
1)先找到前驱或者后继元素,然后使得这个直接前驱或者直接后继元素覆盖掉所要删除的元素的值
2)再把这个直接前驱或者直接后继元素删除
往往非叶子节点的前驱或者后继元素必定在叶子节点中
所以最终的删除前驱或者后继元素,就是最开始提到的情况删除的元素在叶子结点中——往往真正删除的元素都发生在叶子节点中
但是必须要满足对于非根结点,其对应的结点的个数为┌m/2┐-1但是删除后的结点可能不满足这个硬性要求(叶子节点被删掉一个元素后,元素的个数可能会低于最低限制┌m/2┐-1)。此时需要做的操作为因为下溢结点的元素数量必然满足其值等于┌m/2┐-2,所以,如果下溢结点的邻近的兄弟结点,至少有┌m/2┐个元素,那么此时产生下溢的结点可以向其兄弟节点借一个元素——将父结点的元素b插入到下溢结点的0(最小位置),然后用兄弟节点的a(最大的元素)代替父结点中的元素b——这种操作其实满足旋转
但是对于下溢结点其邻近的结点只有┌m/2┐-1个元素的情况——(也就是不能元素借位),选择把中间的父结点的元素b挪下来将左右子节点进行合并,合并后的结点的元素个数┌m/2┐+┌m/2┐-2≤m-1
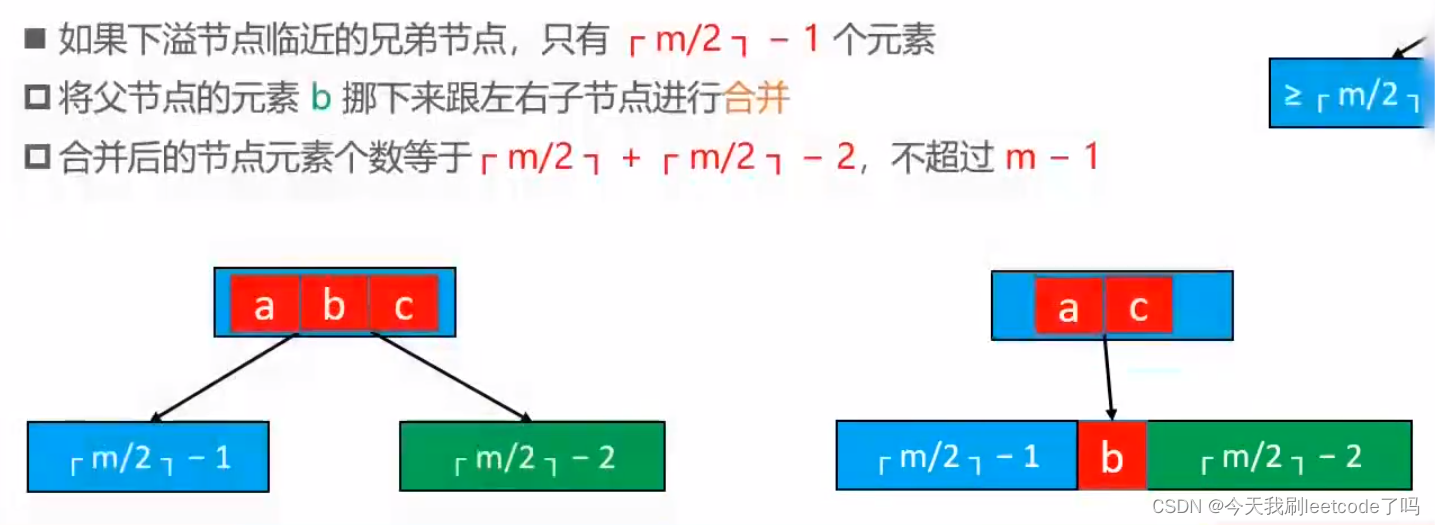
这个可能导致父结点的下溢——依然按照上述的方法解决,下溢现象可能会一直往上传播,最终传播到根结点
唯一一种能够让B树长高的情况——添加元素后,上溢一直持续到根结点
唯一一种能够让B树变矮的情况——删除元素后,下溢一直持续到根结点
同时,在下溢进行右旋转的时候,如果借的兄弟节点的右子树存在,那么这个右子树需要更改插入到已经借结点成功的结点的最左子树——因为从父结点下来的结点,肯定该元素是小于右侧子节点的最小元素值,所以插入0位置,同时原本该父结点的左子树的右子树的值也比该元素小,所以需要插入到该结点元素的最左子树位置