using System;

namespace Zhou.CSharp.Algorithm
{
    /// <summary>
    /// 矩阵类
    /// 作者：周长发
    /// 改进：深度混淆
    /// https://blog.csdn.net/beijinghorn
    /// </summary>
    public partial class Matrix
    {
        /// <summary>
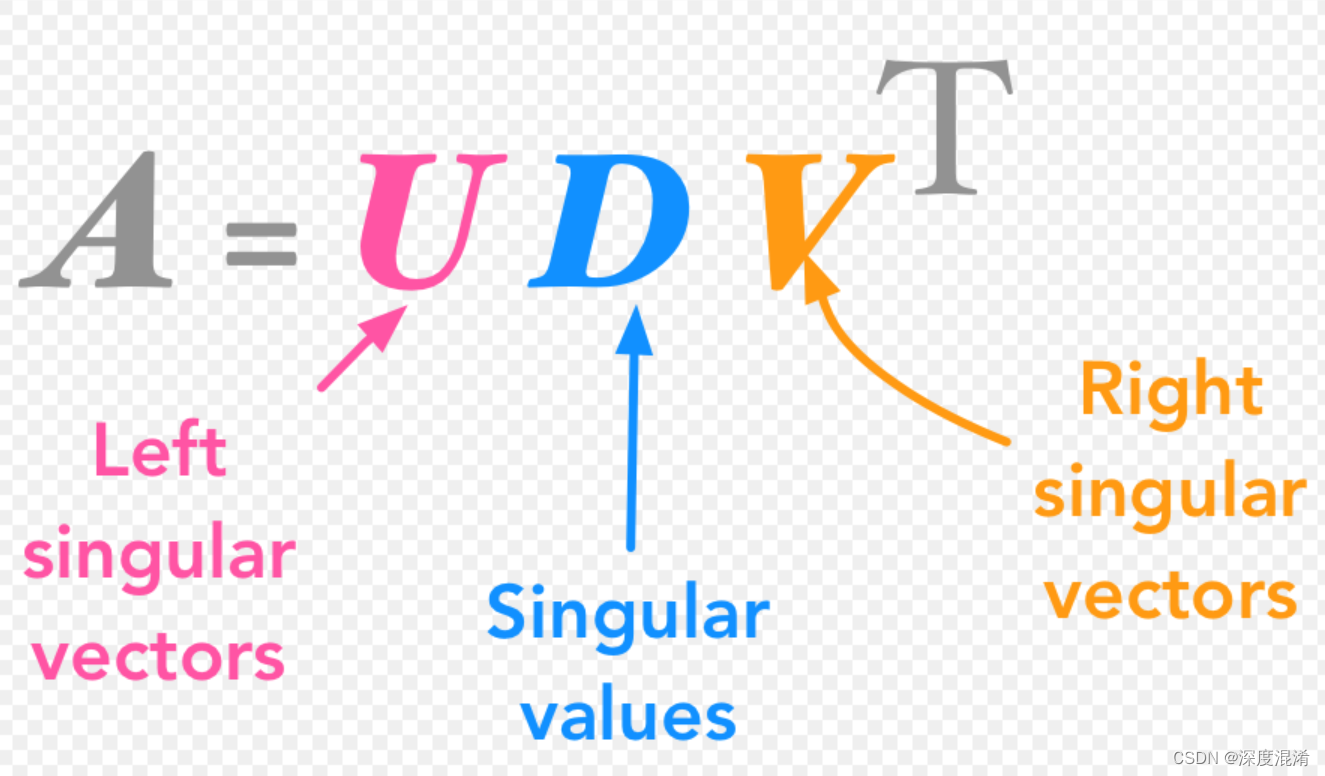
        /// 求广义逆的奇异值分解法，分解成功后，原矩阵对角线元素就是矩阵的奇异值
        /// </summary>
        /// <param name="src">源矩阵</param>
        /// <param name="mtxAP">原矩阵的广义逆矩阵</param>
        /// <param name="mtxU">分解后的U矩阵</param>
        /// <param name="mtxV">分解后的V矩阵</param>
        /// <param name="eps">计算精度</param>
        /// <returns>求解是否成功</returns>
        public static bool InvertUV(Matrix src, Matrix mtxAP, Matrix mtxU, Matrix mtxV, double eps)
        {
            int i, j, k, u, t, p, q, f;

            // 调用奇异值分解
            if (!SplitUV(src, mtxU, mtxV, eps))
            {
                return false;
            }
            int m = src.Rows;
            int n = src.Columns;

            // 初始化广义逆矩阵
            if (!mtxAP.Init(n, m))
            {
                return false;
            }
            // 计算广义逆矩阵

            j = n;
            if (m < n)
            {
                j = m;
            }
            j = j - 1;
            k = 0;
            while ((k <= j) && Math.Abs(src[k * n + k]) > float.Epsilon)//([k * n + k] != 0.0))
            {
                k = k + 1;
            }
            k = k - 1;
            for (i = 0; i <= n - 1; i++)
            {
                for (j = 0; j <= m - 1; j++)
                {
                    t = i * m + j;
                    mtxAP[t] = 0.0;
                    for (u = 0; u <= k; u++)
                    {
                        f = u * n + i;
                        p = j * m + u;
                        q = u * n + u;
                        mtxAP[t] = mtxAP[t] + mtxV[f] * mtxU[p] / src[q];
                    }
                }
            }

            return true;
        }
    }
}