openjudge 1805:碎纸机 解析报告
总时间限制: 1000ms 内存限制: 65536kB
描述
你现在负责设计一种新式的碎纸机。一般的碎纸机会把纸切成小片,变得难以阅读。而你设计的新式的碎纸机有以下的特点:
1.每次切割之前,先要给定碎纸机一个目标数,而且在每张被送入碎纸机的纸片上也需要包含一个数。
2.碎纸机切出的每个纸片上都包括一个数。
3.要求切出的每个纸片上的数的和要不大于目标数而且与目标数最接近。
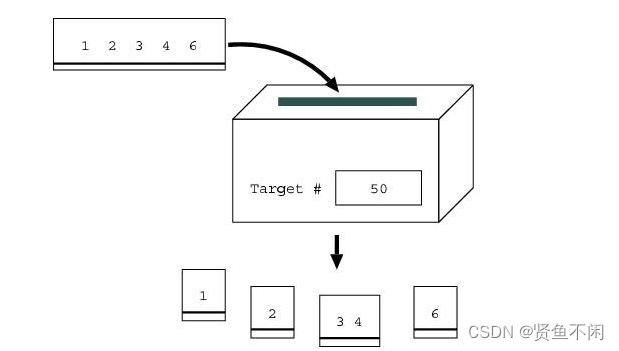
举一个例子,如下图,假设目标数是50,输入纸片上的数是12346。碎纸机会把纸片切成4块,分别包含1,2,34和6。这样这些数的和是43 (= 1 + 2 + 34 + 6),这是所有的分割方式中,不超过50,而又最接近50的分割方式。又比如,分割成1,23,4和6是不正确的,因为这样的总和是34 (= 1 + 23 + 4 + 6),比刚才得到的结果43小。分割成12,34和6也是不正确的,因为这时的总和是52 (= 12 + 34 + 6),超过了50。
还有三个特别的规则:
1.如果目标数和输入纸片上的数相同,那么纸片不进行切割。
2.如果不论怎样切割,分割得到的纸片上数的和都大于目标数,那么打印机显示错误信息。
3.如果有多种不同的切割方式可以得到相同的最优结果。那么打印机显示拒绝服务信息。比如,如果目标数是15,输入纸片上的数是111,那么有两种不同的方式可以得到最优解,分别是切割成1和11或者切割成11和1,在这种情况下,打印机会显示拒绝服务信息。
为了设计这样的一个碎纸机,你需要先写一个简单的程序模拟这个打印机的工作。给定两个数,第一个是目标数,第二个是输入纸片上的数,你需要给出碎纸机对纸片的分割方式。
输入
输入包括多组数据,每一组包括一行。每行上包括两个正整数,分别表示目标数和输入纸片上的数。已知输入保证:两个数都不会以0开头,而且两个数至多都只包含6个数字。
输入的最后一行包括两个0,这行表示输入的结束。
输出
对每一组输入数据,输出相应的输出。有三种不同的输出结果:
sum part1 part2 ...
rejected
error
第一种结果表示:
1.每一个partj是切割得到的纸片上的一个数。partj的顺序和输入纸片上原始数中数字出现的次序一致。
2.sum是切割得到的纸片上的数的和,也就是说:sum = part1 + part2 +...
第一种结果中相邻的两个数之间用一个空格隔开。
如果不论怎样切割,分割得到的纸片上数的和都大于目标数,那么打印“error”。
如果有多种不同的切割方式可以得到相同的最优结果,那么打印“rejected”。
样例输入
50 12346
376 144139
927438 927438
18 3312
9 3142
25 1299
111 33333
103 862150
6 1104
0 0
样例输出
43 1 2 34 6
283 144 139
927438 927438
18 3 3 12
error
21 1 2 9 9
rejected
103 86 2 15 0
rejected
这道题很玄学,因为这道题的数据特别小。所以很水。水来了~水来了~水来了~
虽然全片都没有数据范围。但是这道题的数据位数不超过10.很小很有趣。
而我们的搜索思路就现的很简单了。就是区间内枚举断点。用深搜的思路来枚举断点。
这里有个小小的初始化。map_1[i][j]表示的是从第i到第j位,组成的数字。
举个栗子,12346 中 map_1[1][5]表示的就是12346
这样会方便我们判断,就不用重复的去做拼凑。
dfs(int x ,int y,int k)中。
x代表区间起点。y代表区间的中点。k代表这个区间内断点的数量。
而这里的判断标准就是。当没有断点可以枚举的时候,最后的总和就是这个我们把整个数分解完之后的结果。之和。
而往下传递的时候有很多小细节需要注意。
1,这里面涉及到剪枝.29行里。如果map_1xi这个区间里的数已经比目标数大了或者这个区间和与全面之后也要比目标数大,就没必要再去枚举。毕竟越枚举越大。
2,28行里。y-i<k 这也是个剪枝。这个剪枝就是涉及到当前的区间里的空格数要比目标断点小。这个就塞不进去。。这个式子的原写法是 y-i-1 < k-1 这个写法可能会更好看懂一些。如果你真的列出来。并且画出区间。一目了然/
3,最后就是在输出的时候。每一行最后一定不要多输出空格。不然会WA。会很尴尬。
接下来贴出程序。
#include<cstdio>
#include<algorithm>
#include<string.h>
using namespace std;
int flag=0;
int a[13],ans[13],num[13],max_1,max_z,n;
int map_1[13][13];
int DFS(int x,int y,int k)
{if(k==0){if(map_1[x][y]>max_z||map_1[x][y]+n>max_z)return 0;if(map_1[x][y]+n<=max_z&&map_1[x][y]+n>max_1){num[++num[0]]=map_1[x][y];max_1=map_1[x][y]+n;memcpy(ans,num,sizeof(num));--num[0];flag=0;}else if(map_1[x][y]+n==max_1)//处理重复{flag=1;}return 0;}for(int i=x;i<=y;i++){if(y-i<k)break;if(map_1[x][i]>max_z||map_1[x][i]+n>max_z)break;//越界问题n+=map_1[x][i];num[++num[0]]=map_1[x][i];DFS(i+1,y,k-1);num[num[0]]=0;--num[0];n-=map_1[x][i];}return 0;}int main(){int m,k;while(~scanf("%d%d",&max_z,&m)){if(max_z==0)break;if(max_z==m){printf("%d %d\n",max_z,max_z);continue;}flag=0;max_1=0;n=0;memset(a,0,sizeof(a));memset(map_1,0,sizeof(map_1));memset(num,0,sizeof(num));memset(ans,0,sizeof(ans));for(k=1;m!=0;++k){a[k]=m%10;m/=10;}--k;for(int i=1;i<=k/2;i++)//交换位置不要忘了swap(a[i],a[k-i+1]);for(int i=1;i<=k;++i){for(int j=i;j<=k;++j){map_1[i][j]=map_1[i][j-1]*10+a[j];//初始化断点}}int sum=0;for(int i=1;i<=k;++i){sum+=a[i];}if(sum>max_z){printf("error\n");continue;}for(int i=0;i<=k-1;++i)//枚举断点。这个不能忘。{DFS(1,k,i);}if(flag){printf("rejected\n");continue;}sum=0;for(int i=1;i<=ans[0];++i)sum+=ans[i];printf("%d ",sum);for(int i=1;i<=ans[0];++i){if(i!=ans[0])printf("%d ",ans[i]);else printf("%d\n",ans[i]);}}return 0;
}