[C++]二叉搜索树

一、定义

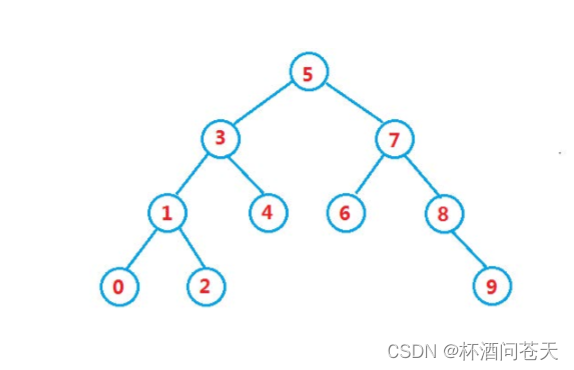
二叉搜索树又称二叉排序树，它或者是一棵空树，或者是具有以下性质的二叉树:

若它的左子树不为空，则左子树上所有节点的值都小于根节点的值
若它的右子树不为空，则右子树上所有节点的值都大于根节点的值
它的左右子树也分别为二叉搜索树

二、插入insert

对于二叉搜索树的插入操作，我们将需要插入的key值与当前结点（初始结点是root结点）比较，若小于该结点的值，则往左子树走；若大于该结点的值，则往右子树走。走到空结点的时候，那么这个位置就是这个key值的归宿。

template<class K, class V>
struct BSTreeNode
{BSTreeNode<K, V>* left;BSTreeNode<K, V>* right;K _key;V _value;
};template<class K, class V>
class BSTree
{typedef BSTreeNode<K, V> Node;
public:BSTree(){_root = nullptr;}bool Insert(const K& key, const V& value){if (_root == nullptr){_root = new Node;_root->_key = key;_root->_value = value;_root->left = nullptr;_root->right = nullptr;}else{Node* cur = _root;Node* parent = _root;while (cur){if (key < cur->_key){parent = cur;cur = cur->left;}else if (key > cur->_key){parent = cur;cur = cur->right;}}cur = new Node;cur->left = nullptr;cur->right = nullptr;cur->_key = key;cur->_value = value;if (key < parent->_key){parent->left = cur;}else{parent->right = cur;}}return true;}
private:Node* _root = nullptr;
};

三、查找操作find

对于二叉搜索树的查找操作，我们将需要查找的key值与当前结点（初始结点是root结点）比较，若小于该结点的值，则往左子树走；若大于该结点的值，则往右子树走。

若走到空，则说明没有这个值，返回空指针。若找到该值，则返回该值的结点。

	Node* Find(const K& key){Node* cur = _root;while (cur){if (key < cur->_key){cur = cur->left;}else if (key > cur->_key){cur = cur->right;}else{return cur;}}return nullptr;}

四、删除操作

	bool Erase(const K& key){Node* cur = _root;Node* parent = _root;while (cur){//若key小于当前结点的值，则往左子树走if (key < cur->_key){parent = cur;cur = cur->left;}//若key大于当前结点的值，则往右子树走else if (key > cur->_key){parent = cur;cur = cur->right;}//若key值与当前结点的值相等，则说明该结点就是需要删除的else{//该结点左右子树皆为空的情况if (cur->left == nullptr && cur->right == nullptr){//直接删除if (key < parent->_key){parent->left = nullptr;}if (key > parent->_key){parent->right = nullptr;}delete cur;}//该结点左子树为空的情况else if (cur->left == nullptr){//将该结点的左子树链接到该结点的父结点的子树上，然后删除该结点if (key < parent->_key)parent->left = cur->right;elseparent->right = cur->right;delete cur;}//该结点右子树为空的情况else if (cur->right == nullptr){//将该结点的右子树链接到该结点的父结点的子树上，然后删除该结点if (key < parent->_key)parent->left = cur->left;elseparent->right = cur->left;delete cur;}//左右子树皆不为空//该情况下，我们需要找到左子树的最大结点/右子树的最小结点//然后将需要删除的结点的值和找到的最大结点/最小结点的值交换//此时我们只需要删除交换之后值为需要删除的数值的结点//这里以与左子树的最大结点交换为例else{//del是之后需要删除的结点Node* del = cur->left;//tmp是需要删除的结点的父结点Node* tmp = del;//找到左子树的最大结点，记录为del，此时tmp为del的父结点while (del->right){tmp = del;del = del->right;}//交换key值swap(cur->_key, del->_key);//如即将被删除的结点有左子树，则将其链接到tmp上if (del->left){tmp->right = del->left;}//否则直接将tmp指向即将被删除的结点的指针置空else{tmp->right = nullptr;}//删除交换key值后的结点delete del;}return true;}}return false;}

五、中序遍历InOrder

使用中序遍历二叉搜索树时，我们得到的是一个递增序列。

	void _InOrder(Node* root){if (root == nullptr){return;}_InOrder(root->left);cout << root->_key << ' ';_InOrder(root->right);}void InOrder(){_InOrder(_root);cout << endl;}

六、完整代码

#include<iostream>
#include<string>template<class K, class V>
struct BSTreeNode
{BSTreeNode<K, V>* left;BSTreeNode<K, V>* right;K _key;V _value;
};template<class K, class V>
class BSTree
{typedef BSTreeNode<K, V> Node;
public:BSTree(){_root = nullptr;}bool Insert(const K& key, const V& value){if (_root == nullptr){_root = new Node;_root->_key = key;_root->_value = value;_root->left = nullptr;_root->right = nullptr;}else{Node* cur = _root;Node* parent = _root;while (cur){if (key < cur->_key){parent = cur;cur = cur->left;}else if (key > cur->_key){parent = cur;cur = cur->right;}}cur = new Node;cur->left = nullptr;cur->right = nullptr;cur->_key = key;cur->_value = value;if (key < parent->_key){parent->left = cur;}else{parent->right = cur;}}return true;}Node* Find(const K& key){Node* cur = _root;while (cur){if (key < cur->_key){cur = cur->left;}else if (key > cur->_key){cur = cur->right;}else{return cur;}}return nullptr;}bool Erase(const K& key){Node* cur = _root;Node* parent = _root;while (cur){//若key小于当前结点的值，则往左子树走if (key < cur->_key){parent = cur;cur = cur->left;}//若key大于当前结点的值，则往右子树走else if (key > cur->_key){parent = cur;cur = cur->right;}//若key值与当前结点的值相等，则说明该结点就是需要删除的else{//该结点左右子树皆为空的情况if (cur->left == nullptr && cur->right == nullptr){//直接删除if (key < parent->_key){parent->left = nullptr;}if (key > parent->_key){parent->right = nullptr;}delete cur;}//该结点左子树为空的情况else if (cur->left == nullptr){//将该结点的左子树链接到该结点的父结点的子树上，然后删除该结点if (key < parent->_key)parent->left = cur->right;elseparent->right = cur->right;delete cur;}//该结点右子树为空的情况else if (cur->right == nullptr){//将该结点的右子树链接到该结点的父结点的子树上，然后删除该结点if (key < parent->_key)parent->left = cur->left;elseparent->right = cur->left;delete cur;}//左右子树皆不为空//该情况下，我们需要找到左子树的最大结点/右子树的最小结点//然后将需要删除的结点的值和找到的最大结点/最小结点的值交换//此时我们只需要删除交换之后值为需要删除的数值的结点//这里以与左子树的最大结点交换为例else{//del是之后需要删除的结点Node* del = cur->left;//tmp是需要删除的结点的父结点Node* tmp = del;//找到左子树的最大结点，记录为del，此时tmp为del的父结点while (del->right){tmp = del;del = del->right;}//交换key值swap(cur->_key, del->_key);//如即将被删除的结点有左子树，则将其链接到tmp上if (del->left){tmp->right = del->left;}//否则直接将tmp指向即将被删除的结点的指针置空else{tmp->right = nullptr;}//删除交换key值后的结点delete del;}return true;}}return false;}void _InOrder(Node* root){if (root == nullptr){return;}_InOrder(root->left);cout << root->_key << ' ';_InOrder(root->right);}void InOrder(){_InOrder(_root);cout << endl;}private:Node* _root = nullptr;
};