摘要:
此研究介绍了考虑机场容量,拥堵以及需求随机性的枢纽网络设计问题(HNDC),其综合考虑了战略和运营层面的决策,提出了基于路径的混合整数二阶锥规划 (SOCP) 。 作者利用 SOCP 对偶性结果,提出了一种基于Benders 分解和列生成的精确算法来解决此问题,并使用机场容量可行方案的特定表征来加速求解过程,同时开发有效的branch-and-cut算法来解决主问题。 作者进行了广泛的数据实验来测试所提出的方法的性能,并根据具体实例得出管理见解,包括枢纽拥塞成本、考虑需求的不确定性以及底层网络的完整性,都会对枢纽网络设计和系统的性能产生重大影响。
关键词:航空航天、枢纽拥堵、网络设计
1. 引言
枢纽在交通领域和电信网络中发挥着关键作用,它是分销网络中的整合点,因此可提供规模经济。枢纽网络在各种现实应用中的广泛使用促使大量学者对枢纽网络设计问题 hub network design problem(HND)的经典方法进行了一些扩展。 在这项研究中,作者重点关注HND问题在枢纽拥塞方向的扩展,因为忽视 HND 的枢纽拥堵会损害系统性能,从而导致总体成本变高以及服务质量变差。决策者可以从战略和运营层面采取措施来避免拥塞。 在战略层面,可以通过考虑拥堵成本和需求不确定性来决定枢纽容量;而在运营层面,可以考虑动态路由和枢纽分配,以最有效的方式选择枢纽容量。 因此作者引入了具有枢纽容量、拥塞和随机需求考虑因素的枢纽网络设计问题 (HNDC) ,以涵盖广泛的战略到运营层面的决策。此问题具有以下关键特征。 (i) 枢纽有容量限制,枢纽的拥塞成本取决于可用容量的使用量。(ii) 网络结构为有向图。 因此底层交通网络可以是complete的,也可以是incomplete的,并且每条边所涉及的成本不必满足三角不等式。若在网络图中所有的点之间都相互连接,则此网络图为complete网络,否则称作incomplete网络。(iii) 从某一起点到终点的OD对 (origin-destination) 路径最多可以访问 κ \kappa κ个枢纽,参数 κ \kappa κ用于限制来自运营商或用户角度的操作要求。(iv) 可以在观察需求后动态分配枢纽和确定 OD 路径,以充分利用网络中的可用容量,同时考虑拥堵和运输成本。HNDC 旨在找到最小化包括开设枢纽、枢纽容量获取、拥塞和运输成本的最佳网络设计。为了对此问题进行建模,作者提出了一种新颖的基于路径的混合整数二阶锥规划(MISOCP),并为其解决方案开发了 Benders 分解方法。 Benders 子问题是基于路径的二阶锥规划 (SOCP),其中使用列生成技术确定最佳路线。 SOCP 的对偶结果用于生成新的列和 Benders cuts。主问题被重新表述,以保证生成容量可行的解决方案,并通过branch-and-cut算法解决。 作者对改编自土耳其 (TR) 数据集以及澳大利亚邮政 (AP) 数据集中的实例进行了广泛的数值实验,从而探究不同因素对最优网络设计的影响。
2. 模型描述
此模型定义在有向图G=(N,A)上,N与A分别代表点集和边集。H为潜在的枢纽点集, L为枢纽的容量层级集合,各层级所对应的容量为 q l q^{l} ql,K为OD对集合,起点与终点分别为 o k o_{k} ok与 d k d_{k} dk。 P k P_{k} Pk为在k-OD对下所有可行的路线集合,作者使用列生成方法 (CG) 来生成所有可行路线。此方法从小集合 P k P_k Pk开始,在此集合中,每组OD对有一个成本无限大的人工路径 p k = { o k , d k } p_k = \{o_k,d_k\} pk={ok,dk},如果新路径 p p p的检验数为负,则其可以被增加到当前 P k P_{k} Pk中。各边单位运输成本为 c i j c_{ij} cij,枢纽的开设成本为 f h l f_{h}^l fhl,枢纽间运输的折扣因子为$\alpha $。
在两阶段随机优化模型中,第一阶段用来确定枢纽位置与容量决策,用二元变量 y h l y_{h}^l yhl来表示大小为l的枢纽是否在h点开放。第二阶段是关于操作层面的路线决策,其中用S表示场景的集合, ϕ s \phi_{s} ϕs为场景s发生的概率,并假设从起点 o k o_{k} ok到目的地 d k d_{k} dk的流量遵循泊松分布,均值为 w k ( s ) w_{k}(s) wk(s)。以下是将HNDC问题转化成二阶段随机混合整数非线性优化模型 (MINLP):
min ∑ h ∈ H ∑ l ∈ L f h l y h l + ∑ s ∈ S ϕ ( s ) ( ∑ h ∈ H ∑ l ∈ L b h u h l ( s ) q l − u h l ( s ) + ∑ k ∈ K ∑ p ∈ P k c p v p ( s ) ) ( 1 ) \min \sum_{h\in H}\sum_{l\in L}f_h^l y_h^l + \sum_{s\in S}\phi(s)\Big(\sum_{h\in H}\sum_{l\in L}b_h\frac{u_h^l(s)}{q^l - u_h^l(s)}+\sum_{k\in K}\sum_{p\in P_k}c_pv_p(s)\Big) \quad (1) minh∈H∑l∈L∑fhlyhl+s∈S∑ϕ(s)(h∈H∑l∈L∑bhql−uhl(s)uhl(s)+k∈K∑p∈Pk∑cpvp(s))(1)
目标函数中第一项是开设新枢纽所需总共的成本,第二项是期望的拥堵成本(此成本函数来源 Elhedhli and Wu (2010),其中 b h b_{h} bh为拥塞成本系数, u h l u_{h}^l uhl为通过具有容量层级l的枢纽h聚合的总流量)与运输成本( v p ( s ) v_p(s) vp(s)为从起点到终点选择路线p的乘客流量分数)。
subject to : ∑ p ∈ P k v p ( s ) = 1 , ∀ k ∈ K , s ∈ S ( 2 ) \text{subject to :} \sum_{p\in P_{k}} v_p(s) = 1, \quad \forall k\in K, s\in S \quad (2) subject to :p∈Pk∑vp(s)=1,∀k∈K,s∈S(2)
此约束确保每个场景s下每个OD对的乘客需求都被满足。
∑ k ∈ K ∑ p ∈ P k : h ∈ p w k ( s ) v p ( s ) = ∑ l ∈ L u h l ( s ) , ∀ h ∈ H , s ∈ S ( 3 ) \sum_{k\in K}\sum_{p\in P_{k}:h\in p} w_k(s)v_p(s) = \sum_{l\in L}u_h^l(s), \quad \forall h\in H, s\in S\quad (3) k∈K∑p∈Pk:h∈p∑wk(s)vp(s)=l∈L∑uhl(s),∀h∈H,s∈S(3)
此约束计算每个场景s中经过每个枢纽的总流量。
u h l ( s ) ≤ q l y h l , ∀ h ∈ H , l ∈ L s ∈ S ( 4 ) u_h^l(s)\leq q^l y_h^l, \quad \forall h\in H, l\in L s\in S\quad (4) uhl(s)≤qlyhl,∀h∈H,l∈Ls∈S(4)
此约束计算每个场景s中每个枢纽的总流量不超过可分配的总容量。
∑ l ∈ L y h l ≤ 1 , ∀ h ∈ H ( 5 ) \sum_{l\in L}y_h^l \leq 1, \quad \forall h\in H \quad (5) l∈L∑yhl≤1,∀h∈H(5)
此约束确保每个枢纽最多可选择一种容量层级。
y h l ∈ { 0 , 1 } ∀ h ∈ H , l ∈ L ( 6 ) y_h^l \in \{0,1\} \quad \forall h\in H, l\in L \quad (6) yhl∈{0,1}∀h∈H,l∈L(6)
v p ( s ) ≥ 0 , ∀ k ∈ K , p ∈ P k , s ∈ S ( 7 ) v_p(s) \geq 0, \quad \forall k\in K, p\in P_k, s\in S \quad (7) vp(s)≥0,∀k∈K,p∈Pk,s∈S(7)
u h l ( s ) ≥ 0 , ∀ h ∈ H , l ∈ L , s ∈ S ( 8 ) u_h^l(s) \geq 0, \quad \forall h\in H, l\in L, s\in S \quad (8) uhl(s)≥0,∀h∈H,l∈L,s∈S(8)
约束 (6) - (8) 为决策变量的取值范围。
由于理论研究的进步和内点法的快速发展,SOCP 技术已被应用于解决广泛的优化问题,作者通过以下方法将非线性从目标函数转化到约束条件,从而得到混合整数二阶锥规划(MISOCP)。
添加人工变量 r h l ( s ) r_{h}^l(s) rhl(s),并添加约束:
r h l ( s ) ≥ 0 , ∀ h ∈ H , l ∈ L , s ∈ S ( 9 ) r_h^l(s) \geq 0, \quad \forall h\in H, l\in L, s\in S \quad (9) rhl(s)≥0,∀h∈H,l∈L,s∈S(9)
r h l ( s ) ≥ u h l ( s ) q l − u h l ( s ) , ∀ h ∈ H , l ∈ L , s ∈ S ( 10 ) r_h^l(s) \geq \frac{u_h^l(s)}{q^l - u_h^l(s)}, \quad \forall h\in H, l\in L, s\in S \quad (10) rhl(s)≥ql−uhl(s)uhl(s),∀h∈H,l∈L,s∈S(10)
将式(10)两边同乘 q l q^l ql后,再加 ( u h l ( s ) ) 2 (u_h^l(s))^2 (uhl(s))2,得到
( u h l ( s ) ) 2 ≤ ( q l r h l ( s ) − u h l ( s ) ) ( q l − u h l ( s ) ) , ∀ h ∈ H , s ∈ S , l ∈ L ( 11 ) (u_h^l(s))^2 \leq (q^lr_h^l(s)-u_h^l(s))(q^l-u_h^l(s)), \quad \forall h\in H,s\in S, l\in L \quad (11) (uhl(s))2≤(qlrhl(s)−uhl(s))(ql−uhl(s)),∀h∈H,s∈S,l∈L(11)
由 ξ 2 ≤ ξ 1 ξ 2 \xi^2\leq \xi_1 \xi_2 ξ2≤ξ1ξ2 可得 可得 可得 ∣ ∣ ( 2 ξ , ξ 1 − ξ 2 ) ∣ ∣ ≤ ξ 1 + ξ 2 ||(2\xi,\xi_1-\xi_2)||\leq \xi_1 +\xi_2 ∣∣(2ξ,ξ1−ξ2)∣∣≤ξ1+ξ2,即式(11)可转化为:
∣ ∣ ( 2 u h l ( s ) , q l r h l ( s ) − q l ) ∣ ∣ ≤ q l r h l ( s ) + q l − 2 u h l ( s ) , ∀ h ∈ H , s ∈ S , l ∈ L ( 12 ) ||(2u_h^l(s),q^lr_h^l(s)-q^l )|| \leq q^lr_h^l(s) +q^l-2u_h^l(s), \quad \forall h\in H,s\in S, l\in L \quad (12) ∣∣(2uhl(s),qlrhl(s)−ql)∣∣≤qlrhl(s)+ql−2uhl(s),∀h∈H,s∈S,l∈L(12)
HNDC可转化为
min ∑ h ∈ H ∑ l ∈ L f h l y h l + ∑ s ∈ S ϕ ( s ) ( ∑ h ∈ H ∑ l ∈ L b h r h l ( s ) + ∑ k ∈ K ∑ p ∈ P k c p v p ( s ) ) ( 13 ) \min \sum_{h\in H}\sum_{l\in L}f_h^l y_h^l + \sum_{s\in S}\phi(s)\Big(\sum_{h\in H}\sum_{l\in L}b_hr_h^l(s)+\sum_{k\in K}\sum_{p\in P_k}c_pv_p(s)\Big) \quad (13) minh∈H∑l∈L∑fhlyhl+s∈S∑ϕ(s)(h∈H∑l∈L∑bhrhl(s)+k∈K∑p∈Pk∑cpvp(s))(13)
subject to : (2)-(9), (12) \text{subject to : (2)-(9), (12)} subject to : (2)-(9), (12)
3. Benders 分解过程
作者使用Benders分解方法将HNDC问题分解为一个主问题 (MP) 以及每个场景下的子问题 (SP),即二元变量y将在MP中被处理,而连续变量u和v将根据MP而确定的枢纽位置和容量决策在子问题中被处理。SP确定每个枢纽的流量以及每组OD对下的路线,以使拥塞和路线成本总和最小化。 对于给定场景s,原锥子问题 (PCSP) 如下图 (14) – (23) 表示,其中 y ˉ h l \bar{y}_{h}^l yˉhl为固定值,约束(18) - (21)表示锥约束。

作者进一步运用对SOCP问题Benders分解中的对偶化形式来求解此问题,令$\gamma_k(s), \delta_h(s), \eta_h^l(s), \mu_h^l(s), v_h^l(s)
$来表示约束(15) - (20)的对偶变量,则对偶锥子问题(DCSP)的表述由上图所示。
HNDC的主问题MP包括枢纽位置和容量分配决策以及用变量 Ω \Omega Ω代表子问题中的拥堵和运输成本,则主问题(MP)的表述由上图所示,其中$\bar\gamma_k^j(s), \bar\eta_h^{lj}(s), \bar\mu_h^{lj}(s), \bar v_h^{lj}(s)
$代表在s场景下子问题中得到的值,J是最优乘子向量的集合,约束(31)代表加入到主问题的最优cuts。
然而,对于从MP中得到的y,如果被分配的枢纽容量不足以满足路线上的所有需求,则一个或多个场景的子问题可能会不可行,因此作者采用线性不等式来增强主问题,线性不等式用来保证枢纽容量在子问题中满足所有需求。用 K i K_i Ki(此处被称作超OD对集)表示终点为i的所有OD对, z ~ h i \tilde{z}_{hi} z~hi表示为终点为i的流量在枢纽h处保留的容量,则主问题MP可被改进为MP-CUT:
MP-CUT: Min (30) \text{MP-CUT: Min (30)} MP-CUT: Min (30)
s.t. ( 31 ) − ( 34 ) , ∑ i ∈ N z ~ h i = ∑ l ∈ L q l y h l , ∀ h ∈ H ( 35 ) \text{s.t.} (31) - (34), \sum_{i\in N}\tilde{z}_{hi} = \sum_{l\in L}q^ly_h^l, \quad \forall h\in H \quad (35) s.t.(31)−(34),i∈N∑z~hi=l∈L∑qlyhl,∀h∈H(35)
∑ h ∈ H ˉ z ~ h i ≥ ∑ k ∈ K i w k ( s ) , ∀ i ∈ N , H ˉ ∈ H i , s ∈ S ( 36 ) \sum_{h\in \bar{H}}\tilde{z}_{hi} \geq \sum_{k\in K_i}w_k(s), \quad \forall i\in N, \bar{H}\in H_i, s\in S \quad (36) h∈Hˉ∑z~hi≥k∈Ki∑wk(s),∀i∈N,Hˉ∈Hi,s∈S(36)
z ~ h i ≥ 0 , ∀ h ∈ H , i ∈ N ( 37 ) \tilde{z}_{hi}\geq 0, \quad \forall h\in H, i\in N \quad (37) z~hi≥0,∀h∈H,i∈N(37)
其中,约束(35)确定了对枢纽的容量分配。约束(36)保证了枢纽容量可行性,此处 H ˉ ⊆ H \bar{H}\subseteq H Hˉ⊆H被称作超OD对集 K i K_i Ki的最小cut集,即对 k ∈ K i k\in K_i k∈Ki的所有路线来说,其通过了至少一个来自 H ˉ \bar{H} Hˉ的枢纽,且 H ˉ \bar{H} Hˉ的任一真子集都无此性质。
4. 数值实验
本文运用TR数据集和AP数据集来探索以下因素对HNDC方案的影响:(1) complete网络与incomplete网络; (2) 反映流量值的需求乘子HDM;(3) 枢纽间运输的折扣因子$\alpha ; ( 4 ) 拥塞成本系数 ;(4) 拥塞成本系数 ;(4)拥塞成本系数b_{h}$。
下图为拥塞成本系数对 TR 实例中的枢纽网络设计和运营成本的影响。其中图(a)反映了 b h b_{h} bh与一条路线上平均通过的枢纽数量的关系;(b)反映了 b h b_{h} bh与路由成本的关系;©反映了当 α \alpha α为0.75时, b h b_{h} bh与容量成本的关系;(d)反映了当 α \alpha α为0.75时, b h b_{h} bh与拥堵成本的关系。
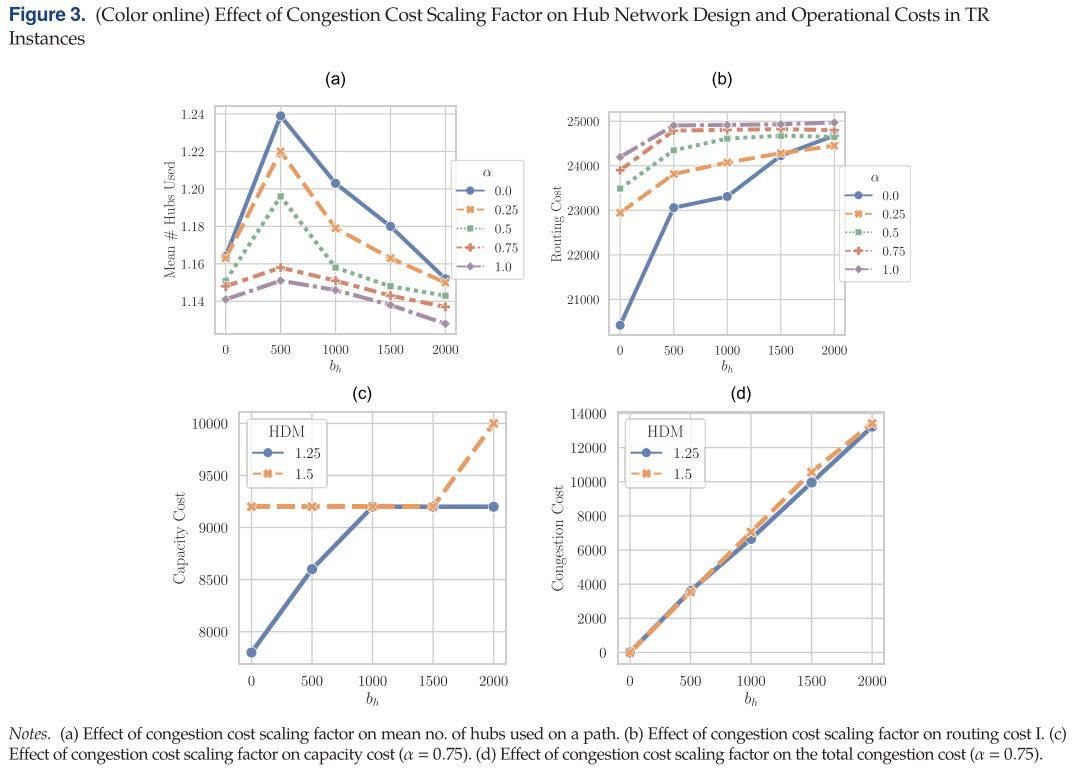
从图(a)可知, b h b_{h} bh与路线上平均通过的枢纽数量之间存在非线性关系。当 b h ≤ 500 b_{h}\leq 500 bh≤500时,随着拥塞成本系数的增加,生成的结果中的路径经过更多的枢纽,因此允许产生更大的路由成本以在一定程度上避免枢纽的拥塞成本。但当 b h > 500 b_{h}>500 bh>500时,拥塞成本对总体成本的贡献较高,模型会尝试使用具有尽可能少枢纽的路径,从而导致路线上平均通过的枢纽数量减少。由图(b)可知,随着枢纽间运输的折扣因子$\alpha 的增加,即客流量汇集带来的规模经济的减少,路由成本也会增加。然而,随着 的增加,即客流量汇集带来的规模经济的减少,路由成本也会增加。 然而,随着 的增加,即客流量汇集带来的规模经济的减少,路由成本也会增加。然而,随着b_{h} 的增加, 的增加, 的增加,\alpha 所带来的路由成本的差异逐渐消失。由图 ( c ) 可知, 所带来的路由成本的差异逐渐消失。由图(c)可知, 所带来的路由成本的差异逐渐消失。由图(c)可知,b_{h} 的增加会导致更高的枢纽容量水平从而对冲枢纽成本的非线性增加。当 H D M 较小时, 的增加会导致更高的枢纽容量水平从而对冲枢纽成本的非线性增加。当HDM较小时, 的增加会导致更高的枢纽容量水平从而对冲枢纽成本的非线性增加。当HDM较小时,b_{h} 的增加会导致更高的容量,而当 H D M 较大时,分配的容量更大, 的增加会导致更高的容量,而当HDM较大时,分配的容量更大, 的增加会导致更高的容量,而当HDM较大时,分配的容量更大,b_{h}$开始只在较高水平上影响容量决策,因为模型生成具有大容量的枢纽网络设计解决方案,以应对不确定的高水平需求,并利用这些额外容量抵御拥堵的风险,直到某一特定程度。这在图(d)中进一步说明了如何通过为较高HDM值分配更多容量,帮助防止拥堵成本的显著增加。图(d)还提示了在设计枢纽网络时要考虑拥堵成本的重要性,否则可能会面临重大损失。
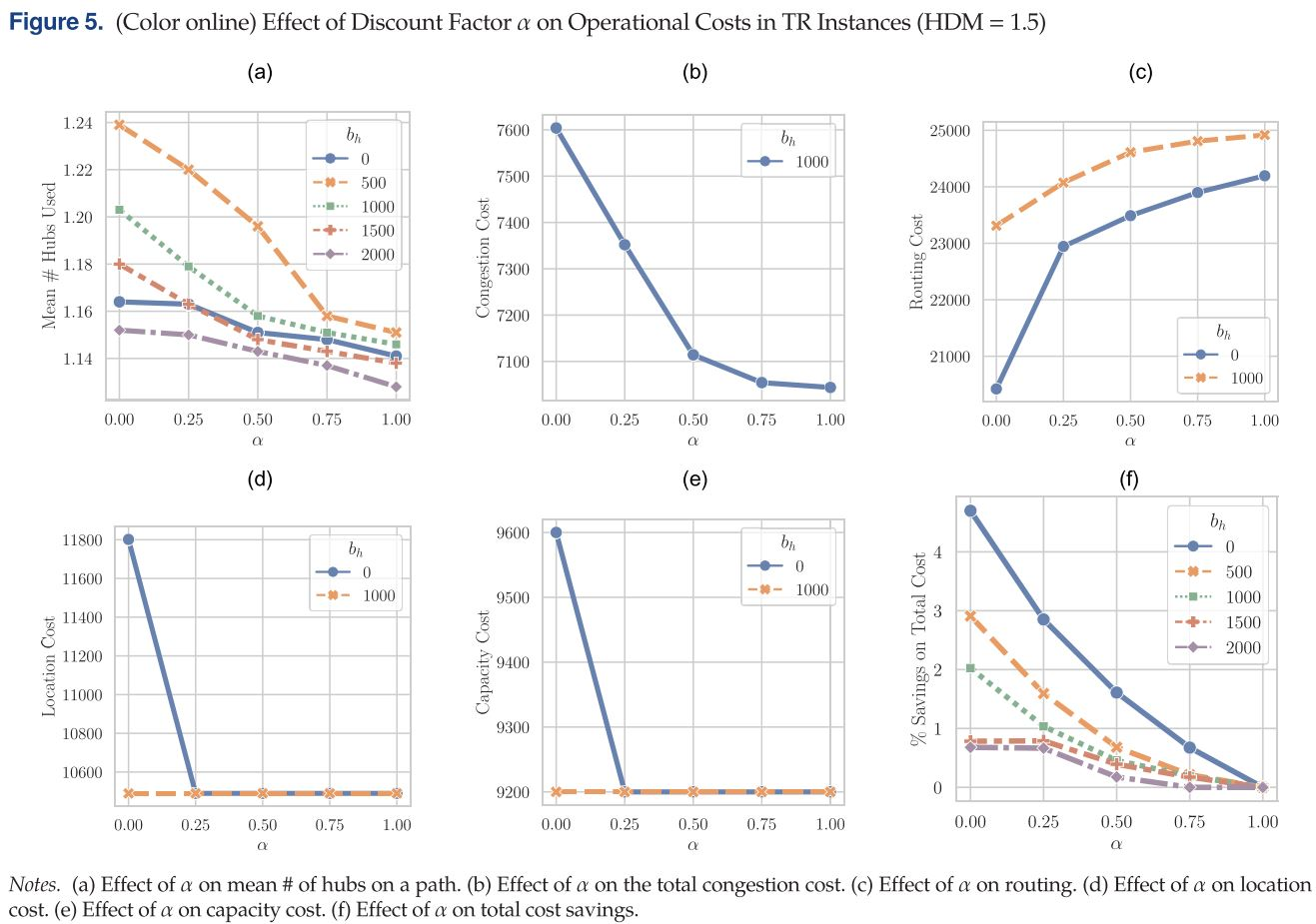
Figure 5. 体现了折扣因子$\alpha 对不同拥塞程度的平均枢纽数量 ( 5 a ) 、拥塞成本 ( 5 b ) 、路由成本 ( 5 c ) 、位置成本 ( 5 d ) 、容量成本 ( 5 e ) 和节省的总成本 ( 5 f ) 的影响。随着折扣因子 对不同拥塞程度的平均枢纽数量 (5a)、拥塞成本 (5b)、路由成本 (5c)、位置成本 (5d)、容量成本 (5e) 和节省的总成本 (5f) 的影响。随着折扣因子 对不同拥塞程度的平均枢纽数量(5a)、拥塞成本(5b)、路由成本(5c)、位置成本(5d)、容量成本(5e)和节省的总成本(5f)的影响。随着折扣因子\alpha 的增加,两个枢纽之间的规模经济优势逐渐减弱,路径上使用的枢纽的平均数量也会减少 ( 5 a ) 。由于规模经济,枢纽间规模经济导致流量整合在枢纽处,从而使枢纽的拥堵成本,路由成本降低,这种权衡体现在 ( 5 b , 5 c ) 。从图 ( 5 d , 5 e ) 中可看出,当 的增加,两个枢纽之间的规模经济优势逐渐减弱,路径上使用的枢纽的平均数量也会减少 (5a)。 由于规模经济,枢纽间规模经济导致流量整合在枢纽处,从而使枢纽的拥堵成本,路由成本降低,这种权衡体现在 (5b, 5c)。从图 (5d, 5e) 中可看出,当 的增加,两个枢纽之间的规模经济优势逐渐减弱,路径上使用的枢纽的平均数量也会减少(5a)。由于规模经济,枢纽间规模经济导致流量整合在枢纽处,从而使枢纽的拥堵成本,路由成本降低,这种权衡体现在(5b,5c)。从图(5d,5e)中可看出,当\alpha 与 与 与b_h 都为 0 时,解决方案中枢纽的数量更多,容量更大,以从规模经济中受益并节省路由成本。随着 都为0时,解决方案中枢纽的数量更多,容量更大,以从规模经济中受益并节省路由成本。随着 都为0时,解决方案中枢纽的数量更多,容量更大,以从规模经济中受益并节省路由成本。随着\alpha 与 与 与b_h 的值变大,总拥塞成本与路由成本变大,解决方案中提供了一种具有更少的枢纽和更小的容量的网络结构,以节省总成本。图 ( 5 f ) 体现出 的值变大,总拥塞成本与路由成本变大,解决方案中提供了一种具有更少的枢纽和更小的容量的网络结构,以节省总成本。图 (5f) 体现出 的值变大,总拥塞成本与路由成本变大,解决方案中提供了一种具有更少的枢纽和更小的容量的网络结构,以节省总成本。图(5f)体现出\alpha 与 与 与b_h 都对总成本有影响,但当 都对总成本有影响,但当 都对总成本有影响,但当b_h 较大时 ( 例如图中所示的 2000 ) , 较大时 (例如图中所示的2000), 较大时(例如图中所示的2000),\alpha 从 0 增加到 0.25 时并不能带来任何显着的净节省,而如果 从0 增加到 0.25 时并不能带来任何显着的净节省,而如果 从0增加到0.25时并不能带来任何显着的净节省,而如果b_h$降低至0,则通过更多地使用枢纽间的路线,总成本可大量减少。
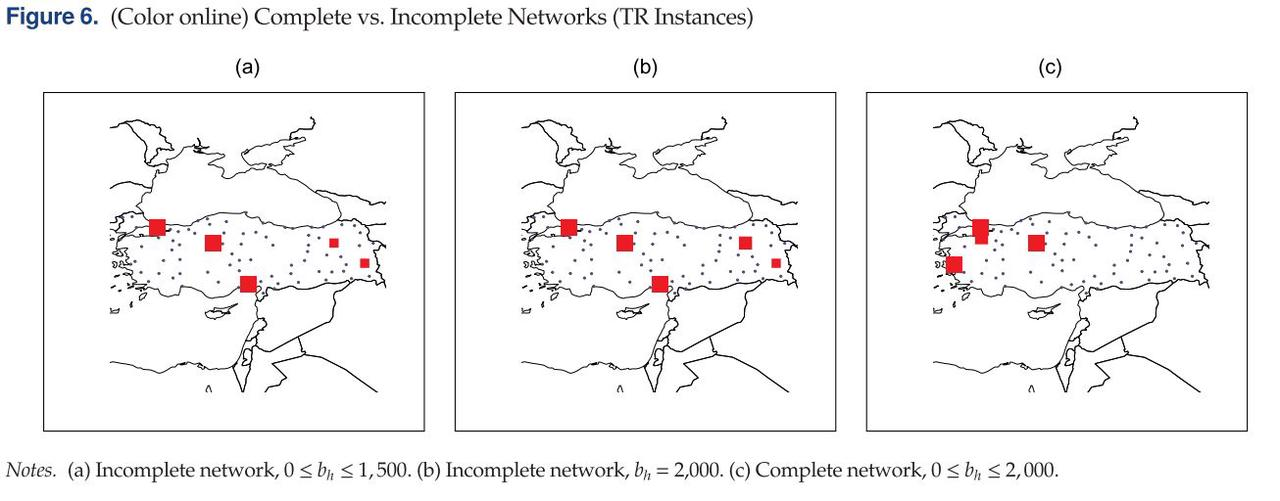
Figure 6. 体现了当 α = 0.75 \alpha =0.75 α=0.75, HDM = 1.5时,使用Complete网络与Incomplete网络下的网络设计差异。正方形所在位置为枢纽位置,正方形面积大小体现了枢纽容量。在Incomplete网络下, b h b_h bh的值影响枢纽容量,不影响枢纽数量。 然而在Incomplete网络下,最终的设计会开设数量较少但容量较大的枢纽,它们主要集中在人口密集的城市。
5. 总结与展望
本研究提出了一种新方法,通过将容量获取决策和拥塞成本整合到经典的枢纽位置问题中来解决枢纽网络设计中的拥塞问题。 作者提出了考虑枢纽拥塞、容量和随机需求的枢纽网络设计问题,它允许根据预期路由和拥塞成本对枢纽位置和容量获取进行动态路由和联合决策。此问题为基于路径的混合整数二阶锥规划,作者开发了一种基于 Benders 分解和列生成的有效求解算法。计算实验表明,考虑拥塞成本和需求的不确定性会导致保留更大的枢纽容量水平,并且当底层网络为incomplete network时,最终生成的网络往往具有更多数量的分散枢纽。 忽略拥塞成本、需求的不确定性和网络结构,会导致总成本更高,甚至可能导致解决方案不可行。 除此之外,决策者需要权衡考虑为了实现枢纽间规模经济而整合的枢纽流量与因流量整合而增加的拥堵成本。在本研究中,作者假设网络设计过程为单阶段,因此未来研究可以扩展到需要分多个步骤构建的网络、需求趋势不断变化且每个阶段使用的资源有限的应用, 同时结合用户反馈和服务质量生成满足需求的网络解决方案。
参考文献:
[1] V. Bayram, B. Yıldız, and M. S. Farham, “Hub network design problem with capacity, congestion, and stochastic demand considerations,” Transportation Science, 2023.
[2] Elhedhli S, Wu H (2010), “ A Lagrangean heuristic for hub-and-spoke system design with capacity selection and congestion,” INFORMS J. Comput. 22(2):282–296.