🌈个人主页:秦jh__https://blog.csdn.net/qinjh_?spm=1010.2135.3001.5343
🔥 系列专栏:《数据结构》https://blog.csdn.net/qinjh_/category_12536791.html?spm=1001.2014.3001.5482

目录
交换排序
快速排序
hoare版代码呈现
快排优化
三数取中法
小区间优化
挖坑法
前后指针版本
非递归版本快排
前言
💬 hello! 各位铁子们大家好哇。
今日更新了快速排序的内容
🎉 欢迎大家关注🔍点赞👍收藏⭐️留言📝
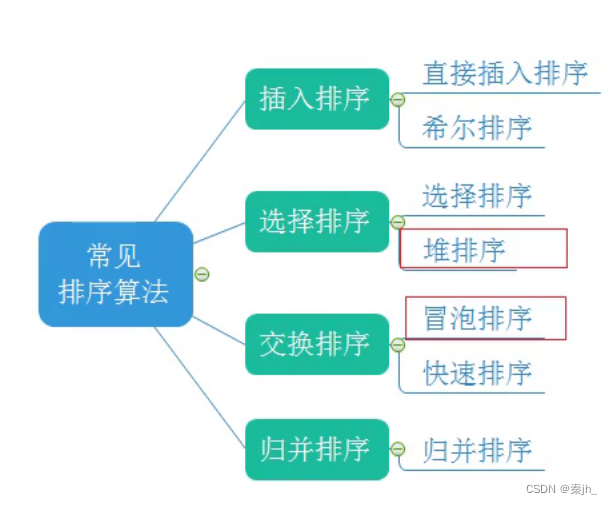
交换排序
快速排序
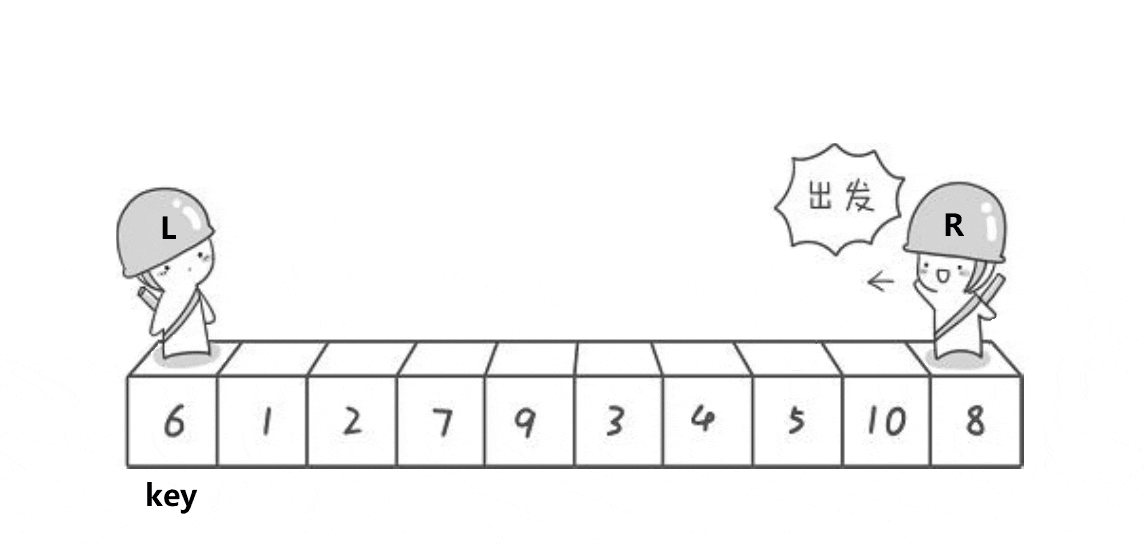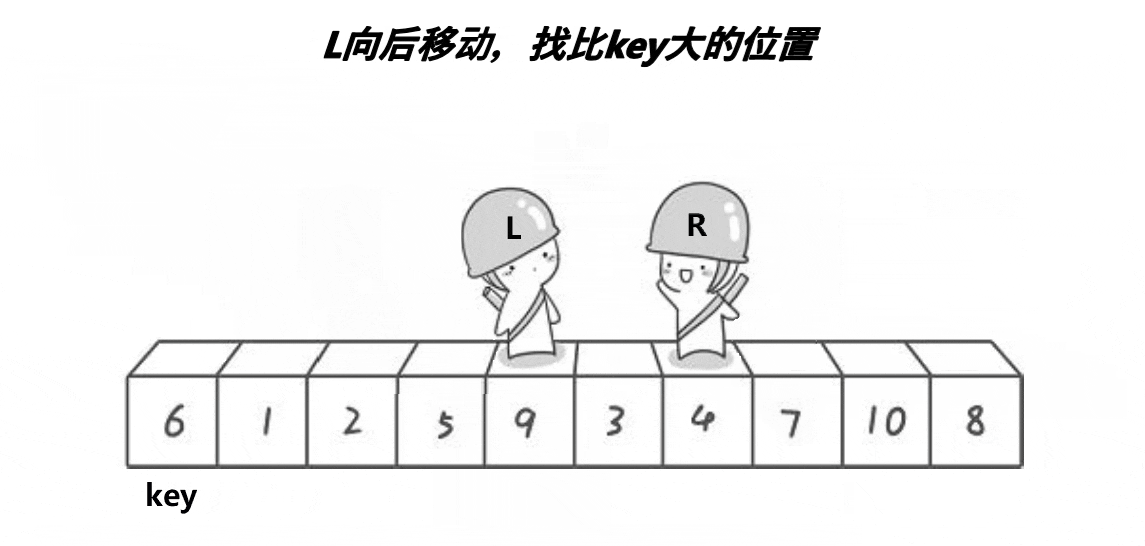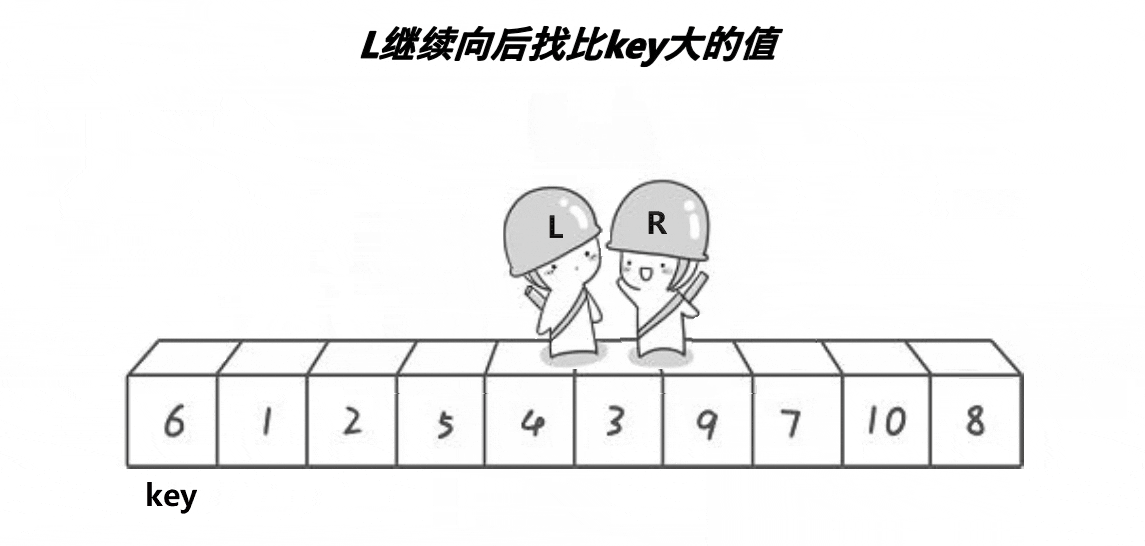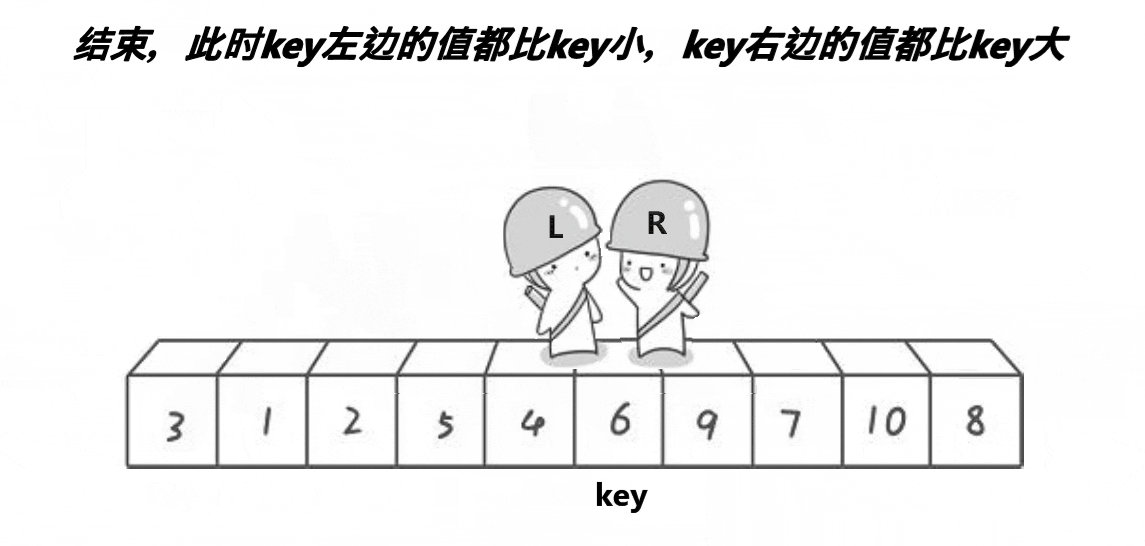
快排的过程图如下:
hoare版代码呈现
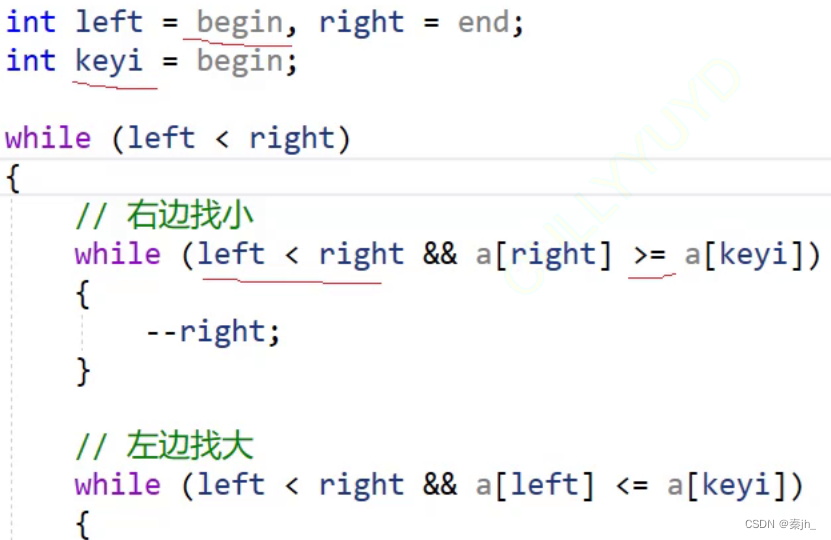
void QuickSort(int* a, int begin,int end)
{if (begin >= end){return;}int left = begin, right =end;int keyi = begin;while (left < right){//右边找小while (left < right && a[right] >= a[keyi]){right--;}//左边找大while (left < right && a[left] <= a[keyi]){left++;}Swap(&a[left], &a[right]);}Swap(&a[left], &a[keyi]);keyi = left;// [begin,keyi-1] keyi [keyi+1,end]QuickSort(a, begin, keyi - 1);QuickSort(a, keyi+1, end);
}分析:快排过程就是左边找比key大的值,右边找比key小的值,找到后就交换。直到left与right相遇,就交换keyi和left对应的值。这是单趟的,后续过程重复,可以思考二叉树的递归过程,快排递归与其相似(见下图)。
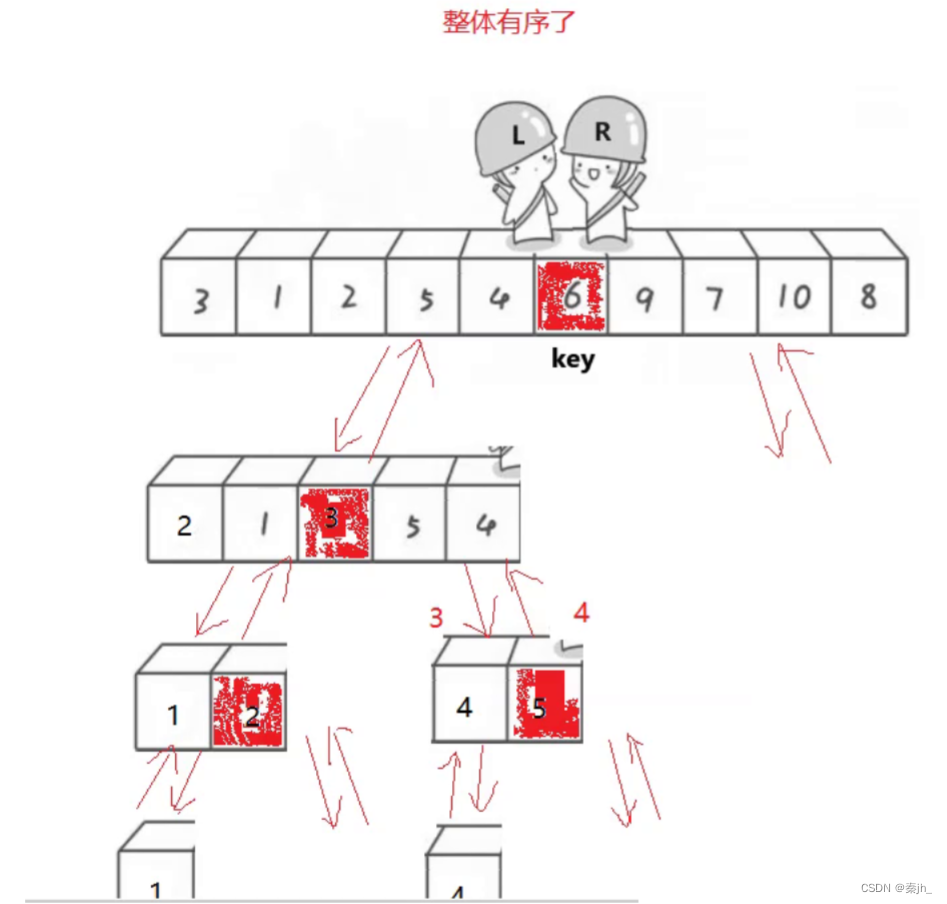
下图中,划红线的地方是容易出错的地方。
理解了前面,这里解释一下为什么相遇位置比keyi位置的值要小?
因为右边先走。
相遇有2种情况
- R遇L->R没有找到比key小,一直走,直到遇到L,相遇位置是L,比key小。
- L遇R->R先走,找到小的停下来了,L找大,没有找到,遇到R停下来了,相遇位置是R,比key小。
如果左边做key,R先走。
如果右边做key,L先走。
快排优化
- 三数取中法选key
- 递归到小的子区间时,可以考虑使用插入排序
三数取中法
快排对于有序的数据,效率不是很高。
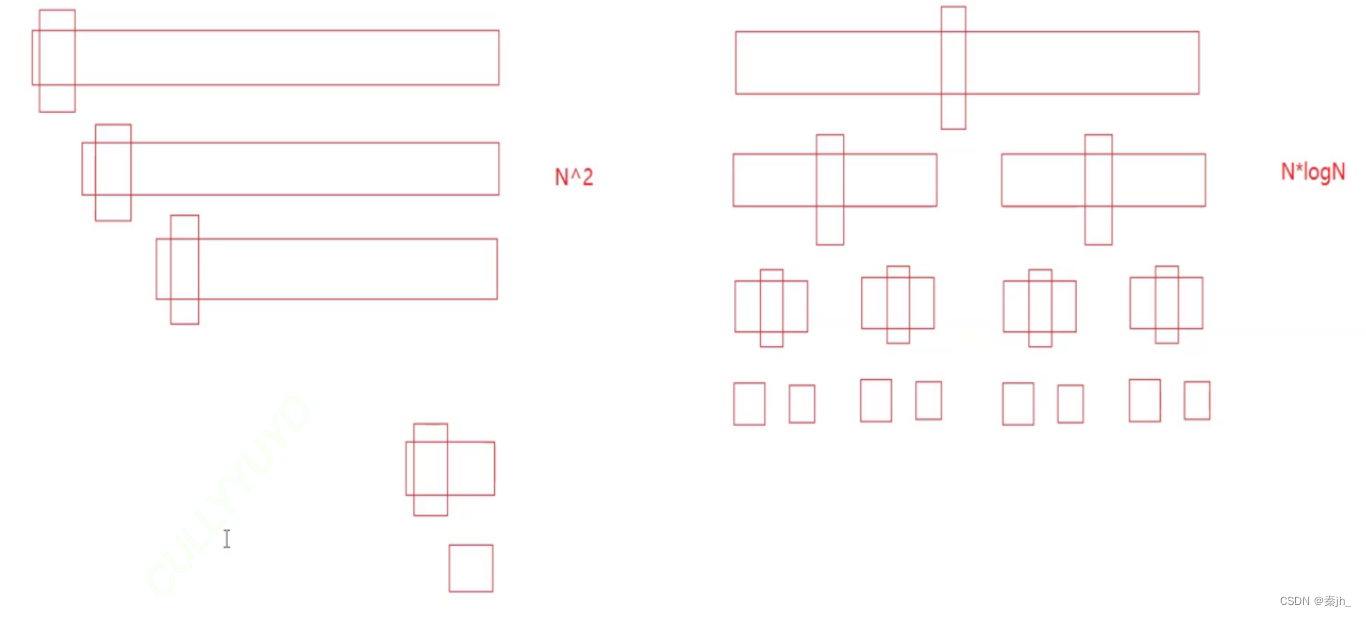
如上图,我们前面的快排是固定选key的,也就是左边第一幅图,效率很低。理想情况下,每一次都二分,这样效率就能提高。这时就用到三数取中法。
三数取中法指三个数里面取中间大小的数,然后将他与key交换位置,让这个中间大小的数作key。
完整代码如下:
int GetMidi(int* a, int begin, int end)
{int midi = (begin + end) / 2;//begin end midi三个数中选中位数if (a[begin] < a[midi]){if (a[midi] < a[end])return midi;else if (a[begin] > a[end])return begin;elsereturn end;}else{if (a[midi] > a[end])return midi;else if (a[begin] < a[end])return begin;elsereturn end;}
}void QuickSort(int* a, int begin, int end)
{if (begin >= end)return;int midi = GetMidi(a, begin, end);Swap(&a[midi], &a[begin]);int left = begin, right = end;int keyi = begin;while (left < right){//右边找小while (left < right && a[right] >= a[keyi]){right--;}//左边找大while (left < right && a[left] <= a[keyi]){left++;}Swap(&a[left], &a[right]);}Swap(&a[left], &a[keyi]);keyi = left;// [begin,keyi-1] keyi [keyi+1,end]QuickSort(a, begin, keyi - 1);QuickSort(a, keyi + 1, end);
}小区间优化
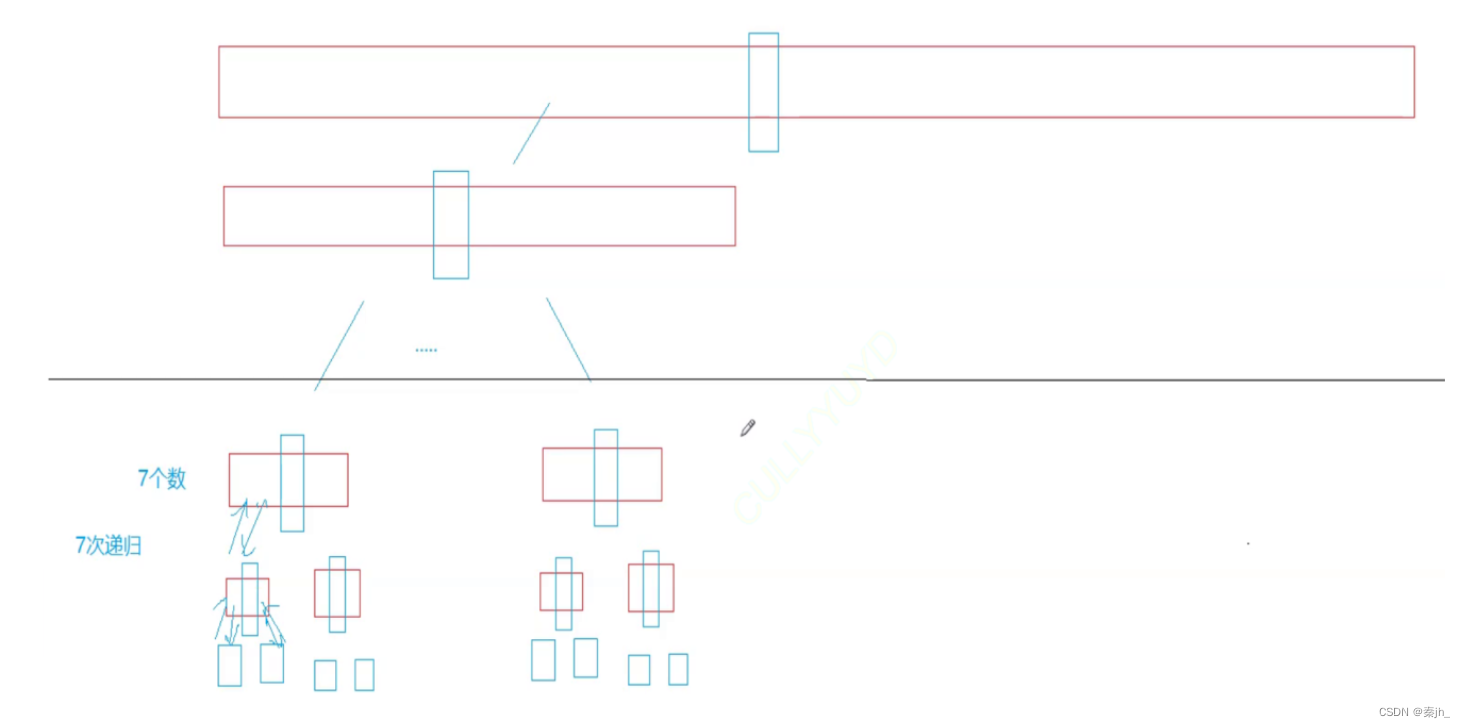
假设在理想情况下,每次递归都像二叉树那样,递归到最后面几层时,假设还剩7个数,我们还得递归7次,这样明显不好。我们就可以在最后几层时,使用其他排序方法进行。这里使用插入排序。
完整代码如下:
void QuickSort(int* a, int begin, int end)
{if (begin >= end)return;if (end - begin + 1 <= 10){InsertSort(a+begin, end - begin + 1);}else {int midi = GetMidi(a, begin, end);Swap(&a[midi], &a[begin]);int left = begin, right = end;int keyi = begin;while (left < right){//右边找小while (left < right && a[right] >= a[keyi]){right--;}//左边找大while (left < right && a[left] <= a[keyi]){left++;}Swap(&a[left], &a[right]);}Swap(&a[left], &a[keyi]);keyi = left;// [begin,keyi-1] keyi [keyi+1,end]QuickSort(a, begin, keyi - 1);QuickSort(a, keyi + 1, end);}
}挖坑法
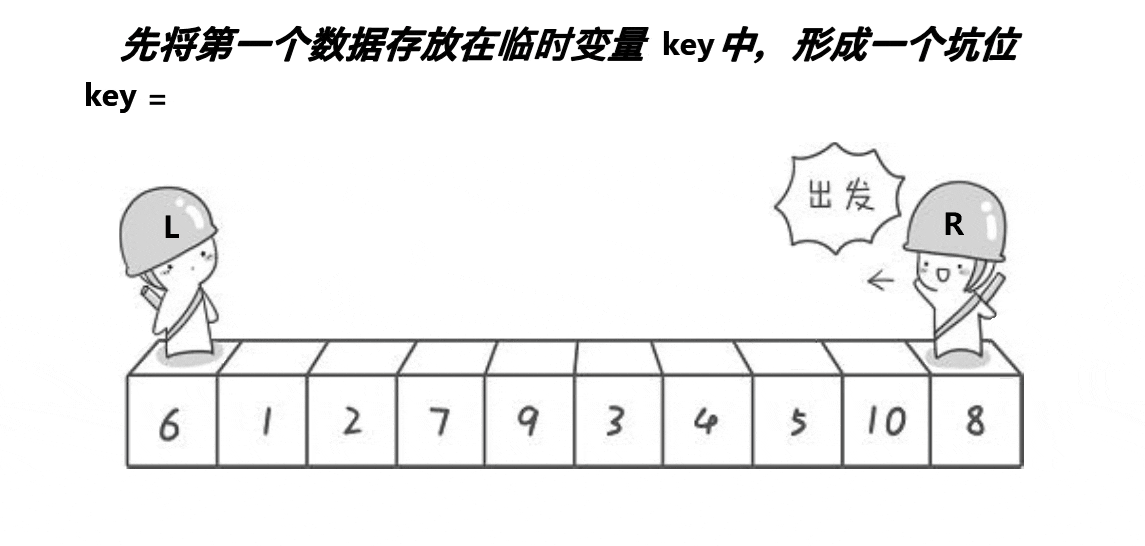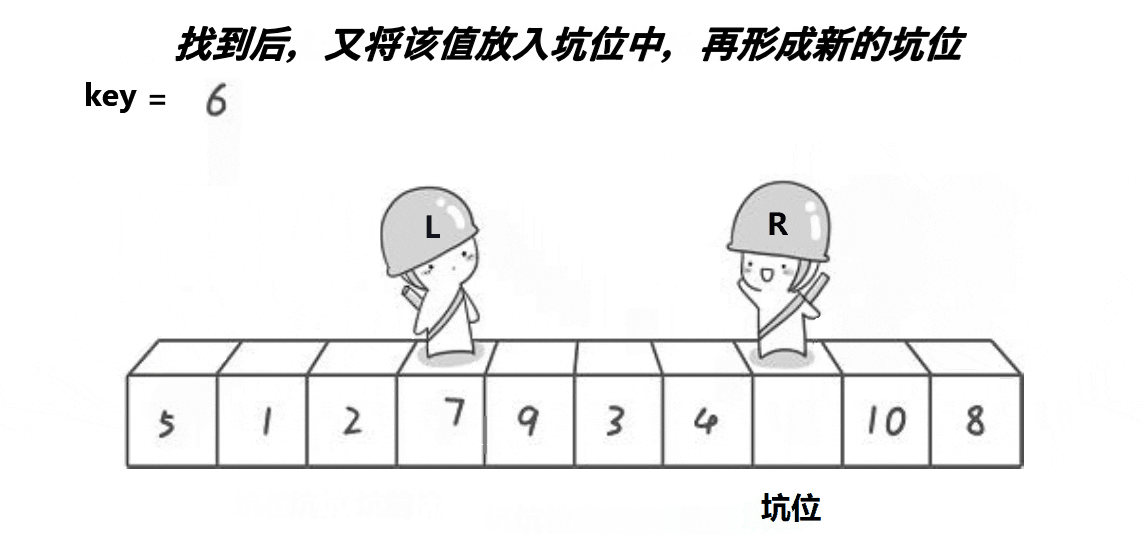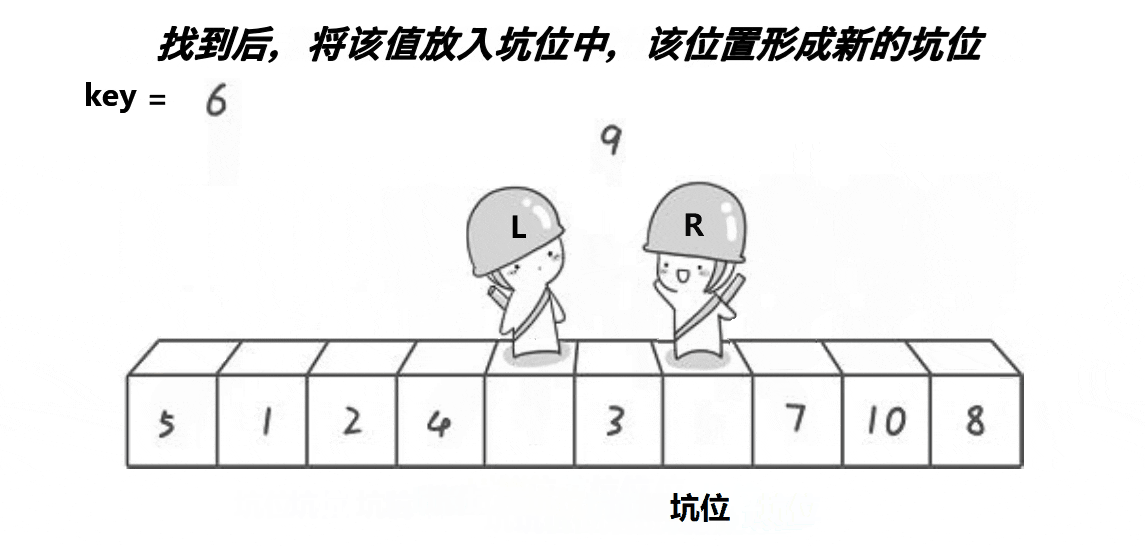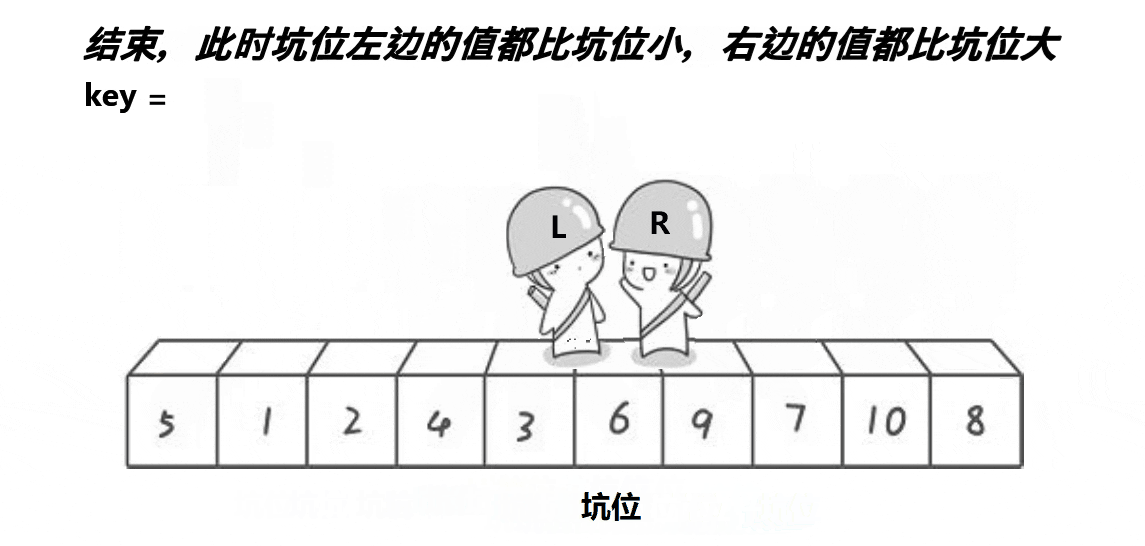
我们把不同方法的单趟排序重新弄成一个函数。
hoare版本:
//hoare版本
int PartSort1(int* a, int begin, int end)
{int midi = GetMidi(a, begin, end);Swap(&a[midi], &a[begin]);int left = begin, right = end;int keyi = begin;while (left < right){//右边找小while (left < right && a[right] >= a[keyi]){right--;}//左边找大while (left < right && a[left] <= a[keyi]){left++;}Swap(&a[left], &a[right]);}Swap(&a[left], &a[keyi]);return left;
}挖坑法完整代码:
//挖坑法
int PartSort2(int* a, int begin, int end)
{int midi = GetMidi(a, begin, end);Swap(&a[midi], &a[begin]);int key = a[begin];int hole = begin;while (begin < end){//右边找小,填到左边的坑while (begin < end && a[end] >= key){end--;}a[hole] = a[end];hole = end;//左边找大,填到右边的坑while (begin < end && a[begin] <= key){begin++;}a[hole] = a[begin];hole = begin;}a[hole] = key;return hole;
} void QuickSort(int* a, int begin, int end)
{if (begin >= end)return;int keyi = PartSort2(a, begin, end);QuickSort(a, begin, keyi - 1);QuickSort(a, keyi+1, end);}
分析:挖坑法其实跟hoare版本比没啥提升,只不过更易理解,本质上没变。但不同的版本,单趟排序后的结果可能会不同。
前后指针版本
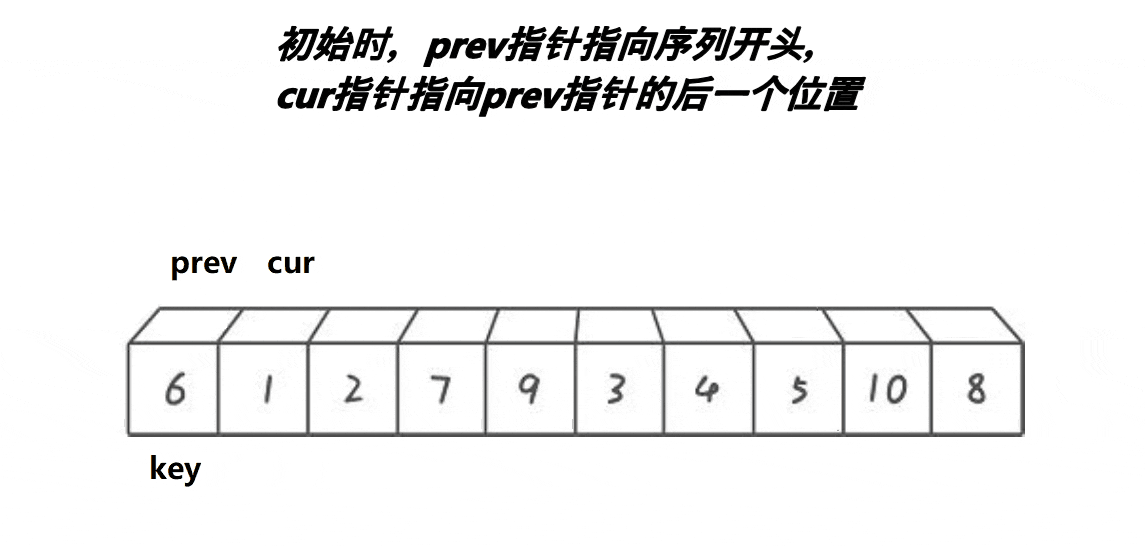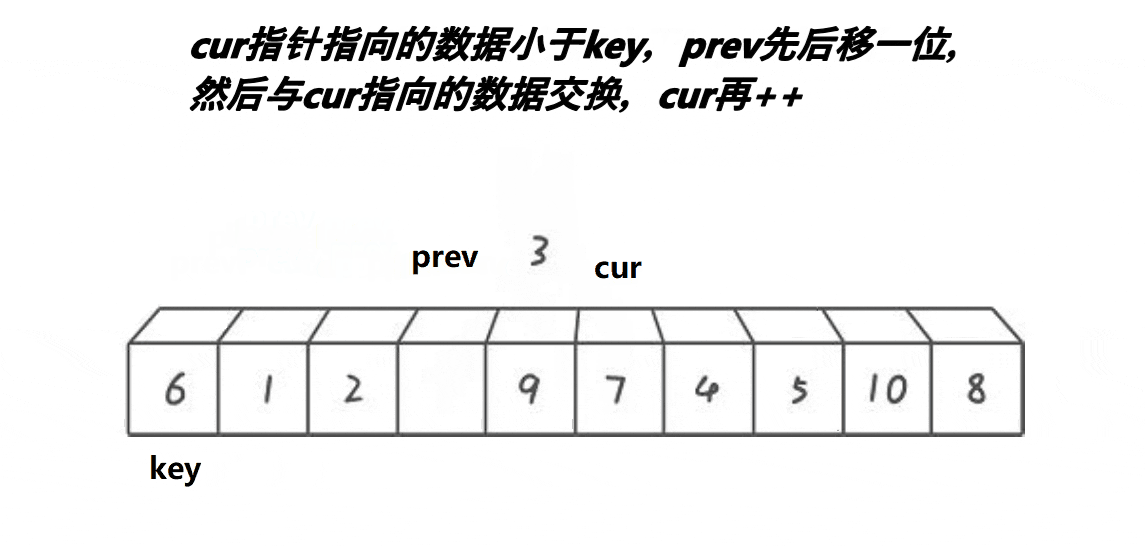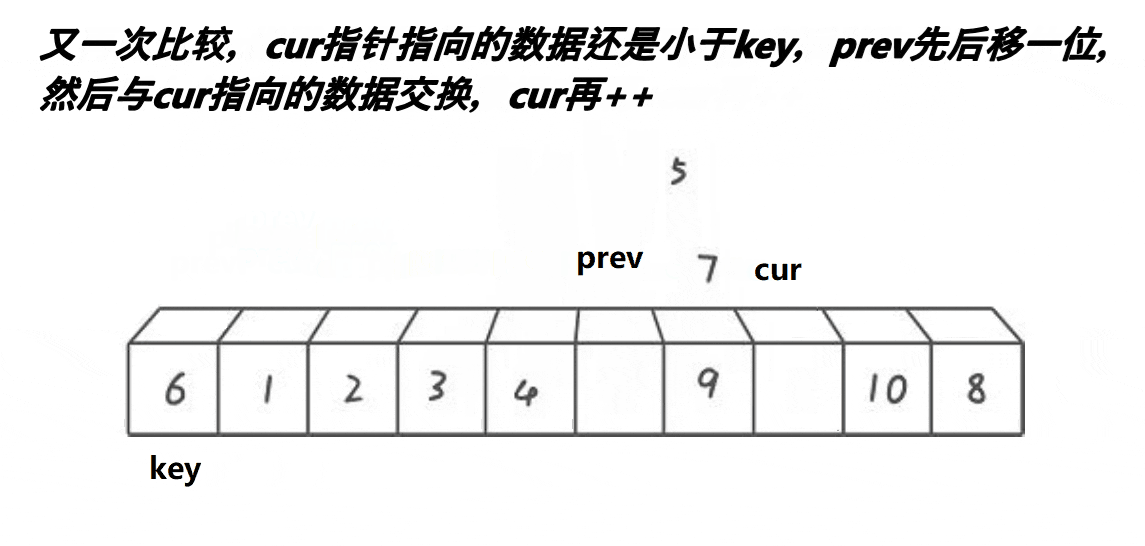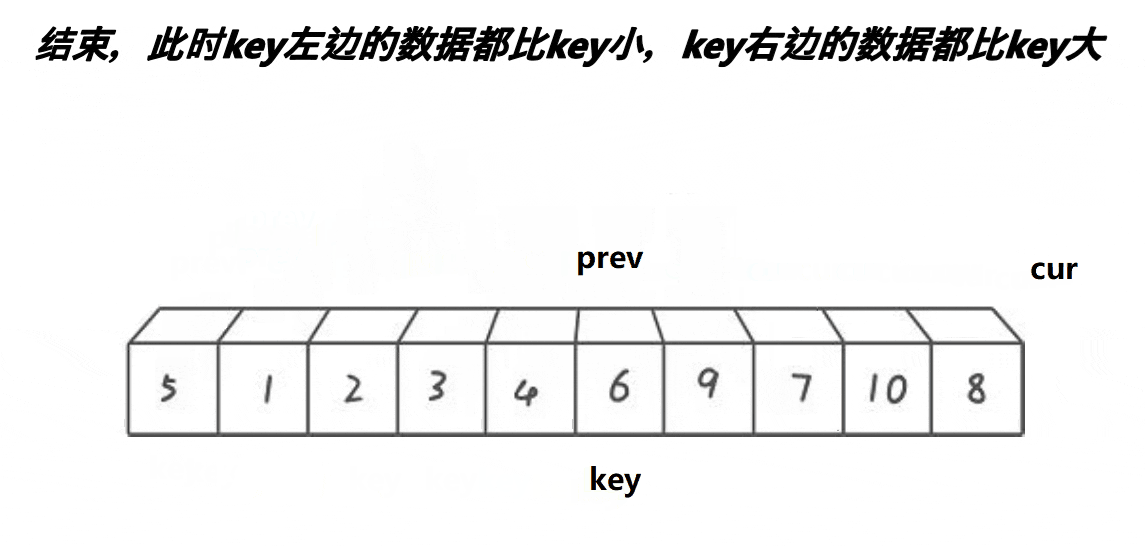
分析:
- cur遇到比key大的值,cur++
- cur遇到比key小的值,++prev,交换prev和cur位置的值,++cur
代码实现
//前后指针法
int PartSort3(int* a, int begin, int end)
{int midi = GetMidi(a, begin, end);Swap(&a[midi], &a[begin]);int keyi = begin;int prev = begin;int cur = prev + 1;while (cur <= end){if (a[cur] < a[keyi] && ++prev!=cur)Swap(&a[prev], &a[cur]);++cur;}Swap(&a[prev], &a[keyi]);keyi = prev;return keyi;
}非递归版本快排
非递归版本的快排需要用到栈。下面给出需要的栈的函数:
void STInit(ST* pst)
{assert(pst);pst->a = NULL;pst->capacity = 0;pst->top = 0;//pst->top = -1;
}void STDestroy(ST* pst)
{free(pst->a);pst->a = NULL;pst->capacity = pst->top = 0;}//栈顶插入删除
void STPush(ST* pst, STDataType x)
{assert(pst);if (pst->top == pst->capacity){int newcapacity = pst->capacity == 0 ? 4 : pst->capacity * 2;STDataType* tmp = (STDataType*)realloc(pst->a, sizeof(STDataType) * newcapacity);if (tmp == NULL){perror("realloc fail");return;}pst->a = tmp;pst->capacity = newcapacity;}pst->a[pst->top] = x;pst->top++;
}void STPop(ST* pst)
{assert(pst);assert(pst->top > 0);pst->top--;
}STDataType STTop(ST* pst)
{assert(pst);assert(pst->top > 0);return pst->a[pst->top - 1];
}bool STEmpty(ST* pst)
{assert(pst);//if (pst->top == 0)//{// return true;//}//else//{// return false;//}return pst->top == 0;
}
非递归代码实现:
void QuickSortNonR(int* a, int begin, int end)
{ST s;STInit(&s);STPush(&s, end);STPush(&s, begin);while (!STEmpty(&s)){int left = STTop(&s);STPop(&s);int right = STTop(&s);STPop(&s);int keyi = PartSort3(a, left, right);// [left,keyi-1] keyi [keyi+1,right]if (keyi+1 < right){STPush(&s, right);STPush(&s, keyi+1);}if (left < keyi - 1){STPush(&s, keyi - 1);STPush(&s, left);}}STDestroy(&s);
}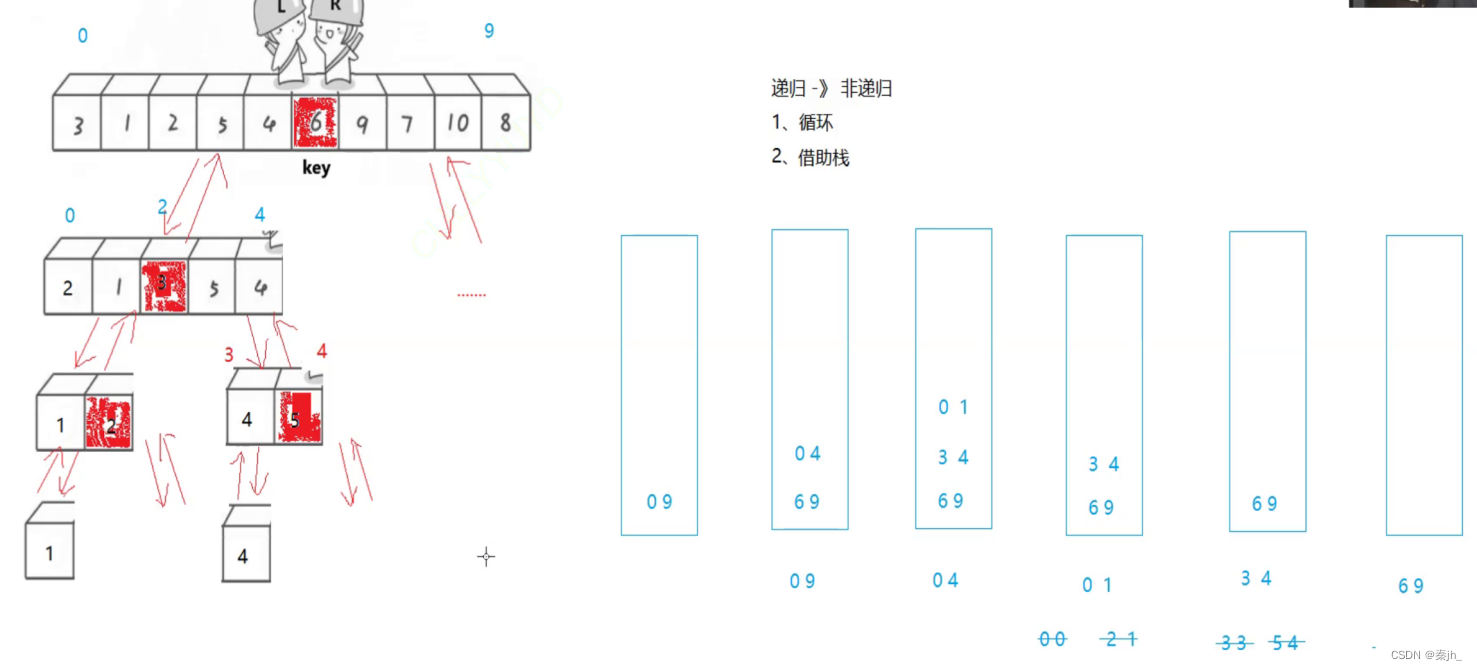
分析:栈是后进先出,这里用栈是模拟递归的过程。先模拟递归左边,像二叉树递归那样,先入右边的数,再入左边,这样出的时候就先出左边的,然后就可以模拟先往左边递归了。