二叉树基础oj题目及思路总结
前文中,介绍了二叉树的基本概念及基础操作,进一步对于二叉树的递归遍历及子问题的处理思想有了一定的了解。本文将带来几道二叉树经典的oj题目。
目录
二叉树基础oj题目
- 对称二叉树
- 平衡二叉树
- 二叉树的层序遍历
二叉树基础oj题目
1、对称二叉树
leetcode题目链接
题目描述:给你一个二叉树的根节点 root , 检查它是否轴对称。如下图就是一颗对称二叉树:
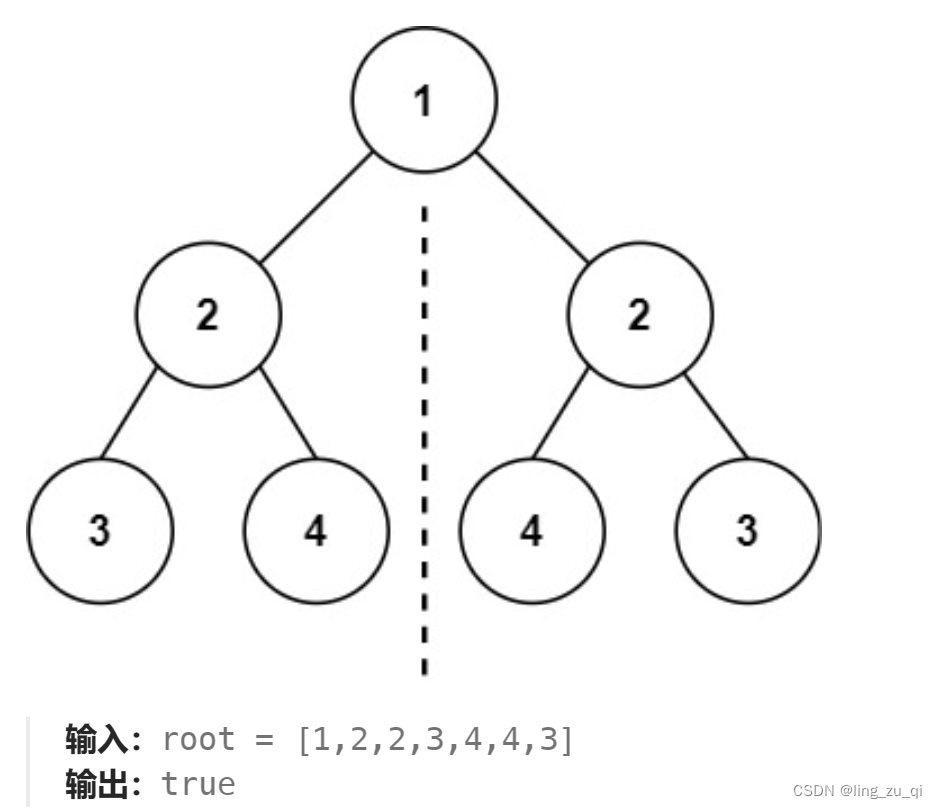
我们可以模拟判断二叉树是不是对称二叉树:
1、对于结点1,左孩子结点为2,右孩子结点为2,目前是对称二叉树。
2、对于1的左孩子结点2,左孩子结点为3,右孩子结点为4, 对于1的右孩子结点2,右孩子结点3,左孩子结点为4,左与右对应,右与左对应,仍是对称二叉树。
可以发现,只要将右子树翻转(左到右,右到左)判断是否与左树相同即可。在总体框架上,仍然使用递归(子问题思路)的方式实现。
public boolean isSymmetric(TreeNode root) {if(root==null) {return false;}return isSameTree(root.left,invertTree(root.right));}public TreeNode invertTree(TreeNode root) {//翻转二叉树if(root==null) return null;TreeNode tep = root.left;//引入tmp结点交换左右结点root.left = root.right;root.right = tep;invertTree(root.left);//递归实现子树的翻转invertTree(root.right);return root;}public boolean isSameTree(TreeNode p, TreeNode q) {//判断左右树是否相同if(p==null&&q!=null||q==null&&p!=null) {//一个为空,一个不为空必不同return false;}if(p==null&&q==null) {return true;}if(p.val!=q.val) {//值不同,结点必不同return false;}return isSameTree(p.left,q.left)&&isSameTree(p.right,q.right);//递归模拟遍历树}
2、平衡二叉树
leetcode题目链接
给定一个二叉树,判断它是否是高度平衡的二叉树。本题中,一棵高度平衡二叉树定义为:
一个二叉树每个节点 的左右两个子树的高度差的绝对值不超过 1。下图就是一颗平衡二叉树。
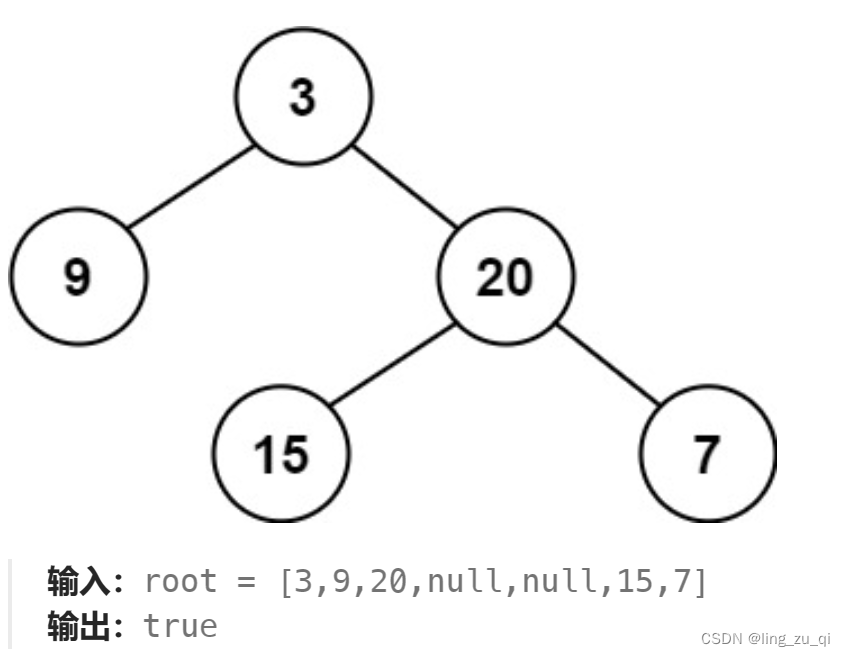
这道题目有两个思路:
- 1、自顶向下的递归
- 2、自底向上的递归
对于自顶向下的递归,需要对于当前遍历到的节点,首先计算左右子树的高度,如果左右子树的高度差不超过1,再分别递归地遍历左右子节点,并判断左子树和右子树是否平衡。这是一个自顶向下的递归的过程。这种递归需要计算每一个结点的高度,时间复杂度较高,为O(N^2)。
而对于自底向上的递归,可以递归地判断其左右子树是否平衡,再判断以当前节点为根的子树是否平衡。如果一棵子树是平衡的,则返回其高度(高度一定是非负整数),否则返回 −1。**如果存在一棵子树不平衡,则整个二叉树一定不平衡。**这种递归方式较为高效,时间复杂度为O(N)。
它们之间的根本区别就是自底向上的递归相较于自顶向下的递归,能够记录下底部的结点构成的子树是不是平衡的,一旦不平衡,就可以直接返回-1,得到这棵树不平衡的结论,可以省去在递归过程中许多重复的计算。下面给出自底向上的递归的代码:
public boolean isBalanced(TreeNode root) {return height(root) >= 0;//不平衡height()返回的是-1}public int height(TreeNode root) {if (root == null) {return 0;}int leftHeight = height(root.left);int rightHeight = height(root.right);if (leftHeight == -1 || rightHeight == -1 //左右子树已经不都平衡,直接返回-1|| Math.abs(leftHeight - rightHeight) > 1) {//从高度上判断树不平衡,返回-1return -1;} else {return Math.max(leftHeight, rightHeight) + 1;//该结点的子树仍平衡,返回最大深度}}
3、二叉树的层序遍历
leetcode题目链接
给你二叉树的根节点 root ,返回其节点值的 层序遍历。(即逐层地,从左到右访问所有节点)。
如下图所示。
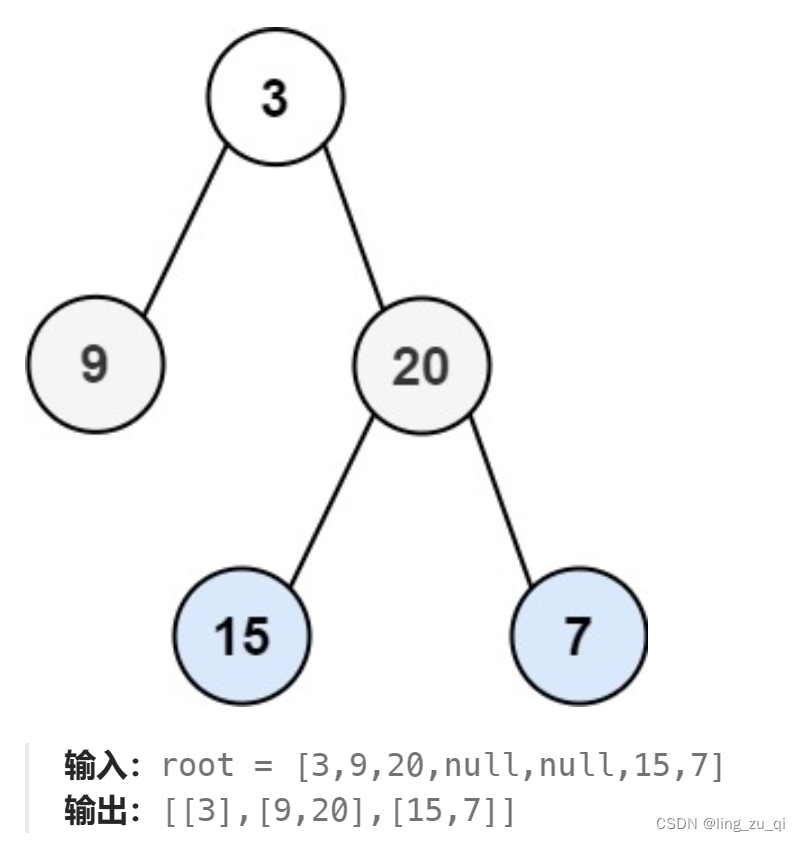
要解决这个问题,似乎我们不能直接通过递归遍历的方式解决。思考一下,第二层的结点都是第一层的根的孩子结点,第三层的根都是第二层的根的孩子结点…而我们打印的顺序也是从上往下打印,有一种先进先出的感觉,这是我们可以考虑使用队列这种数据结构解决问题。
思路:
**对于第一个结点:1、为空,直接return返回。2、不为空,进入队列。
1、循环条件:队列不为空。2、获取队列长度size。3、判断刚入队结点的左孩子结点与右孩子结点,将不为空的结点入队列。4、将size个结点出队列,并输出这些结点的值。当队列为空时,输出结束。**下面是具体代码的呈现:
public List<List<Integer>> levelOrder(TreeNode root) {//返回的实际上是一个二维数组List<List<Integer>> list = new ArrayList<>();if(root==null) {return list;}Queue<TreeNode> q = new LinkedList<>();//队列中放的是结点,泛型规定为TreeNodeq.offer(root);while(!q.isEmpty()) {//队列不为空List<Integer> l = new ArrayList<>();int size = q.size();//获取队列长度while(size!=0) {TreeNode cur = q.poll();l.add(cur.val);if(cur.left!=null) {//判断左孩子是否为空q.offer(cur.left);}if(cur.right!=null) {//判断右孩子是否为空q.offer(cur.right);}size--;}list.add(l);//将一维顺序表加到list中}return list;}