1.1 CartPole-v0
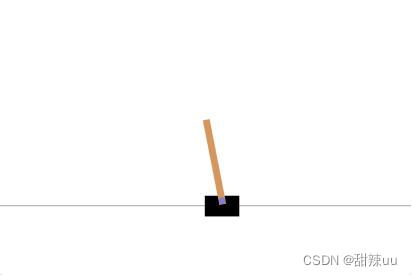
Cart Pole 在 OpenAI 的 gym 模拟器里面是相对比较简单的一个游戏。游戏里面有一个小车,上有 一根杆子。小车需要左右移动来保持杆子竖直。如果杆子倾斜的角度大于 15°,那么游戏结束。小车也不 能移动出一个范围(中间到两边各 4.8 个单位长度)。小车的状态变量有车的位置、杆子的角度、车速、角 度变化率 4 个维度,以及左移、右移两个动作。左移或者右移小车的 action 之后,env 都会返回一个 +1 的 reward。到达 200 个 reward 之后,游戏也会结束。
2 算法
2.1 Q-Learning 算法摘要
Q-Learning 是一种简单而有效的强化学习算法,它不需要对环境进行建模,即使是对带有随机因素 的状态转移概率矩阵或者收益函数也不需要进行特别的改动。对于任何有限马尔可夫决策过程(Finite MDP),给定一个部分随机的策略和无限的探索时间,Q-Learning 都能找到一个可以最大化所有步骤期 望收益的策略。
Q-Learning 的核心是 Q-Table。Q-Table 行和列分别表示 state 和 action 的值,Q(s, a) 衡量对状态 s 采取动作 a 的价值,然后我们可以根据 Q 值来选取某一状态下能获得最大收益的动作。在训练过程中, 我们使用 Bellman Equation 去更新 Q-Table:Q(s, a) = r + γ maxa Q(s′, a′)。考虑到学习率和收益折扣 因素,实际应用中 Q-Table 更新的基本公式为:
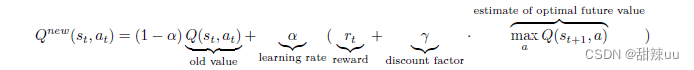
一般 Q-Learning 方法的算法如下:

2.2 Gradient Policy 算法摘要
策略梯度法与上述两种方法有很大不同,后两种方法优化的重点落在了值函数上,不论是 Q-Learning 还是 DQN,只要能够得到精确的值函数,就可以使用 Bellman 公式求出最优策略,即 a = arg max Q(s, a), a = π(s)
策略梯度法则使用另一种思路:强化学习的目标是最大化长期期望收益,即
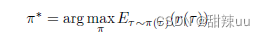
其中 τ 表示用策略进行交互得到的一条轨迹,r(τ ) 表示这条轨迹的总体回报。该目标实际上也是一 个函数,假如这个函数性质良好,其实可以考虑用梯度上升方法对其进行优化。具体而言:如果我们可以 讲值函数表示为策略参数的某个函数,就可以求出值函数关于策略参数的梯度,并使参数沿着梯度上升 的方向更新,从而提升策略。
用 J (θ) 表示上述目标函数,则有
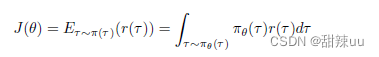
对上式求导,由于策略函数通常是定义良好的函数,所以求导和积分运算可以互换,这样可以得到
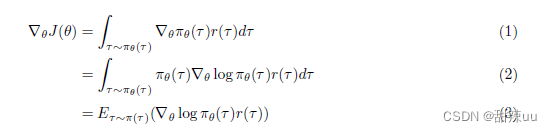
再配合一些技巧,可以将上式拆解。最后,我们再使用蒙特卡洛法,将公式中的期望用蒙特卡洛近似 方法进行替代,可以得到求解梯度的最终式
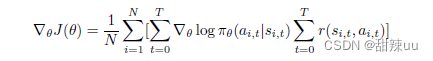
完成了对梯度的求解,接下来便是参数更新。总结起来,Policy Gradient 方法分为两步:
计算 θ J (θ)
θ = θ + α**θ J (θ)
2.3 DQN 算法摘要
Q-Learning 用表格来存储每一个状态 state、每一个行为 action 所拥有的 Q 值,对于状态、动作空 间都为低维离散空间的问题,Q-Learning 不失为一种好方法。但对于连续的状态空间,或是过大的离散 状态空间,用表格来存储会占用大量内存,而且每次在这么大的表格中搜索也分困难。一种解决方法就 是价值函数近似(Value Function Approximation),即学习 f (s, a, w) 使得 Q(s, a) ≈ f (s, a, w)。
机器学习中,神经网络可以很好地近似函数。因此,我们可以将状态和动作当作输入,经过神经网络 计算后得到动作的 Q 值。这样我们就避免了用表格记录 Q 值,而是直接用神经网络生成 Q 值。这种方 法将 Q-Learning 和 Neural Network 的优势结合起来,这便是 DQN(Deep Q Network)方法。
神经网络训练是一个有监督问题,所以我们需要大量的有标签数据。对此,我们可以考虑利用 Q- Learning 的思想为 Q 网络提供有标签数据。Q-Learning 的更新公式为 Q(S, A) = (1 α)Q(S, A)+ α(R + γ maxa Q(S′, a)),我们的优化目标是让 Q 值趋近目标 Q 值 R + γ maxa Q(S′, a),所以目标 Q 值便可作 为标签。自然的,Q 网络的损失函数可以定义为 Es[(R + γ maxa′ Q(s′, a′, w) Q(s, a, w))2]。这样,DQN 的算法框架基本成型。
Q-Learning 方法是一种在线学习方法,每一次模型利用交互生成的数据进行学习,学习后的样本就 被直接丢弃。但如果 DQN 也采用这样的在线学习方法,就可能遇到两个问题:
1.交互得到的序列存在一定的相关性:对机器学习模型来说,训练样本独立同分布是一个基本假设。 而交互序列中状态、动作存在一定的相关性,这样会导致学习得到的值函数模型存在很大的波动。
2.交互数据的使用效率:采用梯度下降法进行参数更新时,模型训练往往需要多轮迭代才能收敛,如 果每次计算的样本在更新完一次梯度后就被丢弃,那么我们就需要花费更多时间与环境交互并收集样本。
为了解决这两个问题,DQN 提出者 Minh V 等人 [2] 采用了 Replay Buffer 这个数据结构,其交互 流程如下:
可以看出,Replay Buffer 保存了交互的样本信息,一般来说每个样本都会保存当前状态 s、行动 a 和长期累积回报。一般可以将 Replay Buffer 的大小设置得比较大,这一较长时间的样本都可以被保存起 来。训练值函数时,我们就可以从中取出一定数量的样本,根据样本记录的信息进行训练。
总体而言,Replay Buffer 包括收集样本和采样两个过程。收集样本时按照时间先后顺序存入结构中, 如果 Replay Buffer 已经存满,新的样本就会按时间顺序覆盖旧样本。另外,Replay Buffer 每次会从缓存 中随机均匀采一批样本进行学习。这样每次训练的样本通常来自多次交互序列,避免了交互序列的相关 性问题。同时一份样本也可以被多次训练,提高了样本的利用率。
3 实验结果分析
3.1 Q-Learning
由于普通的 Q-Learning 算法是一种表格形式的 Agent,所以我们有必要对状态空间进行离散化。为 此,我们用”bins=numpy.linspace(statemin,statemax,num)” 和”numpy.digitize(x,bins)” 函数对状态中的 各个特征值进行离散化处理,分成 0*,* 1*,* 2*,* *...,* *num* 1 共 num 种离散的特征,故而对应的总状态个数为 *num*4 种状态。注意到离散化状态的形式,我们用 num 进制离散状态进行整合,得到一个整数,而这个

整数由于进制的性质,与状态是一一对应的,并且是从 0 开始连续增加的正整数,故而建立 Q-table 其 索引与整合后的状态值一一对应。代码种重要的 Q-Learning 更新过程如下:

此外,上述的 action 选择中用的是 ** greedy:

运行代码,对于 num=10,num=20,我们得出以下关于 episode 和 reward 的折现图。可以看出,刚 开始随着时间的运行,Q-Learning 能很好地想着最优策略的方向学习,使得相应的 reward 不断增加,但 是到达一定训练后,策略提升的速度开始放缓,此外不断地震荡;同时,对比 num 不同的两种情况,我 们可以看出状态空间的精确度提高,的确对策略的提升有正面的影响。
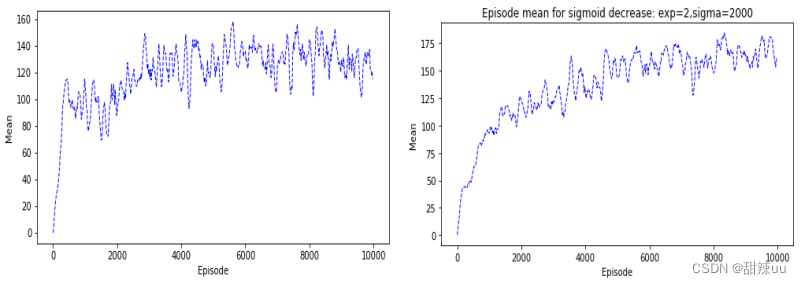
Figure 1: Q-Learning for num=10,num=20
依照 Singh[3] 提出的渐近行为探索策略,我们对上述的 ** greedy 策略添加 sigmoid 类渐近机制,
如下所示:
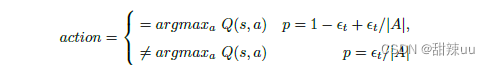
其中
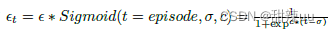
。我们取

= 2000,c = 2, 对 num=10 和 num=20 有以下结果:显然,添加 sigmoid 等函数使得-greedy 的随机性随着训练减小,有利于最终学习算法的收敛和稳定。
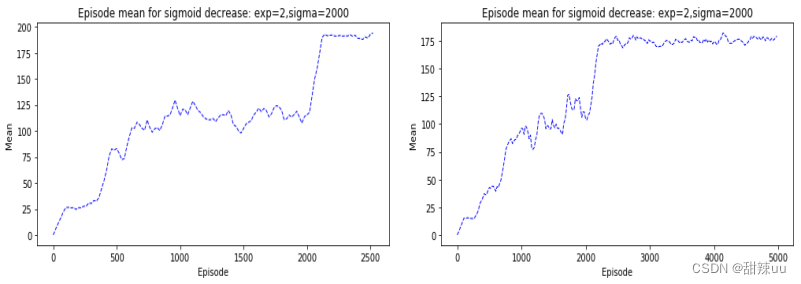
Figure 2: Q-Learning for num=10,num=20 with sigmoid decrease
由于 CartPole-v0 环境中对失败状态的 reward 为-1,对学习的惩罚激励影响较小,所以我们对最后 失败状态的 reward 调整为 reward = 10,最终对 num=10 下,sigmoid 衰减的学习结果如下:可以看出,适当增大失败惩罚有利于学习的高效性,使得学习到更好的结果。
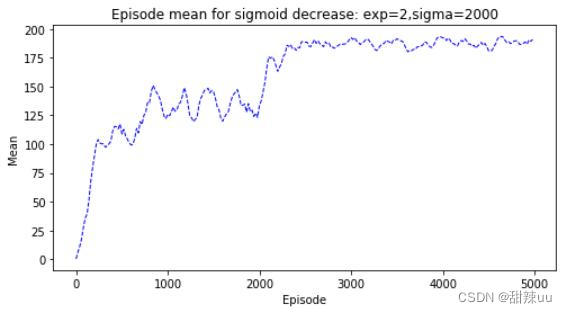
Figure 3: Q-Learning for num=10 with sigmoid decrease
3.2 Policy-Gradient
我们参考了 Morvanzhou 的代码框架,调参、改进并修正了源代码的一些错误,最终完成了自己的代 码并且得到了更好的效果,以下开始分析:
首先,我们定义了一个具有三个全连接层和一个 softmax 输出层的神经网络取逼近策略。Hornik[1] 证明了对于单隐层的三层神经网络,只要中间隐层个数充分大,激活函数为单调连续增加的,那么其在 input×output 上的连续可微函数空间是稠密的,即可以充分近似其上的连续可微连续函数。故而,我们前三个全连接层以 Relu 为激活函数,对于多隐层的神经网络避免的梯度消失情况,减少了变量依赖,提高了运算效率;其次以 softmax 层为输出,得到了输入为状态,输出为动作值概率的函数。
其次,由 Policy Gradient 算法,我们的更新需要涉及到策略(神经网络)的梯度,同时后面还有一 个价值函数对步长和方向进行修正。但是在代码中,我们给出的先是交叉熵损失函数
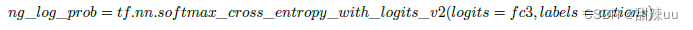
换言之,我们认为实际运行中的动作是理想的,那么实际动作就成为了一个概率(但是是确定的), 类似 极大似然估计,我们的目标就成为更新参数,使得概率最大(等价于交叉熵最小);此外,再通过添加一 个价值函数对更新的步长和方向进行修正,从似然函数的角度,步长为正,越大,那么更新的方向朝着使 得交叉熵最小,未来期望回报增大的方向,对于步长为负,越小的情况,有相反的效果。
此外,由于单纯用蒙特卡洛模拟代价是较大的,为此,我们先通过当前的轨迹回报序列,计算出该场 景下的每个时刻的值函数(注意是该时刻的,即知识单纯地对未来的时刻汇报做指数相加),此外,为了 基于以上的值函数训练,我们将它们通过减去均值,除以方差的“正则化”处理,其关于实际的值函数是无 偏的,同时又降低了方差,使得其能够代替实际的值函数,运用到上述损失函数中。实验中发现这种方法 的确会带来好的效果,但是不敢保证在更复杂空间的可行性。
实验结果如下所示:
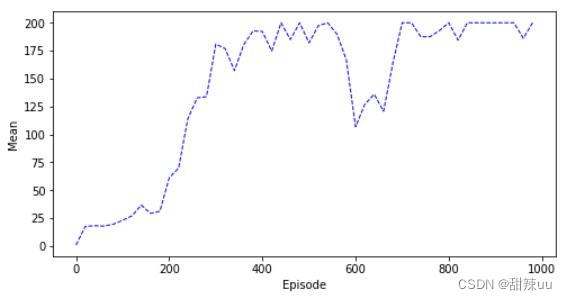
Figure 4: Q-Learning for num=10 with sigmoid decrease
通过此和之前值函数的方法进行比较,可以看出,基于策略梯度的算法在收敛上明显快于值函数方 法,此外其可以在连续的状态空间上进行处理。但是通过运行结果发现,其经常在稳定一段时间后出现一 小段的波动,可能是由于步长的选择,表示策略的函数过于复杂导致的。从这个角度讲,单纯的策略梯度 方法鲁棒性有所欠缺。在基于策略梯度使得梯度单调提升的方向上,目前 TRPO,GAE,PPO 等优秀算 法,这是值的仔细探究的。
3.3 Deep-Q-Network
我们参考 Flood Sung 的代码框架,调参、改进并修正了原代码的一些错误,取得了不错的结果。DQN 与 Q-Learning 都基于 Q-Table 框架,算法原理多有类似,下面就一些 DQN 算法的独特之处进行分析。 在 cartpole 问题中,状态空间是连续的,而 DQN 能处理连续的状态,所以不必像 Q-Learning 一样 对状态空间进行离散化。我们构造了一个 DNN 网络来作为价值函数 Q(s, a) 的近似:将 4 维的状态作为输入,中间 2 层为 20 节点的隐藏层,输出层维度为 2,即与动作空间维度相同。
每个 episode 的每一步,actor 以一定概率随机生成动作,其他情况下按照网络的近似给出最优动作。 收到环境给出收益后,将状态、动作、收益、下一步状态记录下来,提供给网络训练。经过调参和测试,
我们得到图 5 所示结果:
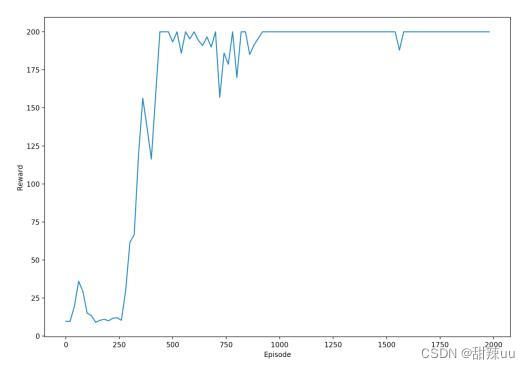
Figure 5: DQN
完整代码:https://download.csdn.net/download/qq_38735017/87391949


![[Linux]进程概念以及进程状态](https://img-blog.csdnimg.cn/344e7b45e32f4042ab62a76d42887351.png)