K-D Tree 算法

　　 $\mathrm{k-d\ tree}$ 即 $\mathrm{k-dimensional\ tree}$ ，是一种分割k维数据空间的数据结构，常用来多维空间关键数据的搜索(如：范围搜素及近邻搜索)，是二叉空间划分树的一个特例。通常，对于维度为 $k$ ，数据点数为 $N$ 的数据集， $\mathrm{k-d\ tree}$ 适用于 $N \gg 2^k$ 的情形。

k-d tree算法原理

　　为了避免比较生硬苦涩的文字说明，这里我采用简单的例子表明 $\mathrm{k-d\ tree}$ 算法。假设有6个二维数据点 $\left \{ (2,3),(5,4),(9,6),(4,7),(8,1),(7,2)\right \}$ 数据点位于二维空间内(如图1所示)。k-d树算法就是要确定图1中这些分割空间的分割线(多维空间即为分割平面，一般为超平面)。下面就要通过一步步展示k-d树是如何确定这些分割线的。

图1 二维数据k-d树空间划分示意图
　　

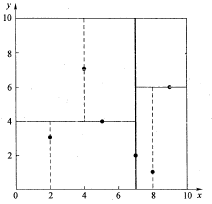
k−d tree k − d t r e e $\mathrm{k-d\ tree}$ 算法可以分为两大部分，一部分是有关k-d树本身这种数据结构建立的算法，另一部分是在建立的k-d树上如何进行最邻近查找的算法。

k-d树构建算法

　　首先列出构建k-d树的伪代码见表1，其中k-d树每个节点中主要包含的数据结构见表2。(参考于王永明王贵锦编著的《图像局部不变特性特征与描述》)

表1 构建k-d树的伪码

算法：构建k-d树（createKDTree）
输入：数据点集Data-set和其所在的空间Range
输出： Kd，类型为Kd-tree
1 If Data-set 是空的，则返回空的 Kd-tree
2 调用节点生成程序：　　（1）确定split域：对于所有描述子数据（特征矢量），统计它们在每个维上的数据方差。以SURF特征为例，描述子为64维，可计算64个方差。挑选出最大值，对应的维就是split域的值。数据方差大表明沿该坐标轴方向上的数据分散得比较开，在这个方向上进行数据分割有较好的分辨率；　　(2）确定Node-data域：数据点集Data-set按其第split域的值排序。位于正中间的那个数据点被选为Node-data。此时新的Data-set’ = Data-set\Node-data（除去其中Node-data这一点）。
3 　　dataleft = {d属于Data-set’ && d[split] ≤ Node-data[split]} 　　Left_Range = {Range && dataleft} 　　dataright = {d属于Data-set’ && d[split] > Node-data[split]} 　　Right_Range = {Range && dataright}
4 left = 由（dataleft，Left_Range）建立的k-d tree，即递归调用createKDTree（dataleft，Left_ Range）。并设置left的parent域为Kd； right = 由（dataright，Right_Range）建立的k-d tree，即调用createKDTree（dataleft，Left_ Range）。并设置right的parent域为Kd。

表2 k-d树中每个节点的数据类型

域名	数据类型	描述
Node-data	数据矢量	数据集中某个数据点，是n维矢量（这里也就是k维）
Range	空间矢量	该节点所代表的空间范围
split	整数	垂直于分割超平面的方向轴序号
Left	k-d树	由位于该节点分割超平面左子空间内所有数据点所构成的k-d树
Right	k-d树	由位于该节点分割超平面右子空间内所有数据点所构成的k-d树
parent	k-d树	父节点

以上述举的实例来看，过程如下：

　　由于此例简单，数据维度只有2维，所以可以简单地给 $x，y$ 两个方向轴编号为 $0,1$ ，也即split= $\left \{0,1\right\}$ 。
　　（1）确定split域的首先该取的值。分别计算 $x，y$ 方向上数据的方差得知 $x$ 方向上的方差最大，所以split域值首先取 $0$ ，也就是 $x$ 轴方向；
（2）确定Node-data的域值。根据 $x$ 轴方向的值 $2,5,9,4,8,7$ 排序选出中值为 $7$ ，所以Node-data= $(7,2)$ 。这样，该节点的分割超平面就是通过 $(7,2)$ 并垂直于split = $0$ ( $x$ 轴)的直线 $x = 7$ ；
　　（3）确定左子空间和右子空间。分割超平面 $x = 7$ 将整个空间分为两部分，如图2所示。 $x \leq 7$ 的部分为左子空间，包含3个节点 $\left \{(2,3),(5,4),(4,7) \right \}$ ；另一部分为右子空间，包含2个节点 $\left \{(9,6),(8,1) \right \}$ 。

图2 x=7将整个空间分为两部分
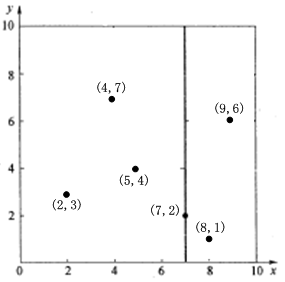
　如算法所述，k-d树的构建是一个递归的过程。然后对左子空间和右子空间内的数据重复根节点的过程就可以得到下一级子节点

(5,4) ( 5 , 4 ) $(5,4)$ 和

(9,6) ( 9 , 6 ) $(9,6)$ （也就是左右子空间的’根’节点），同时将空间和数据集进一步细分。如此反复直到空间中只包含一个数据点，如图1所示。最后生成的k-d树如图3所示。
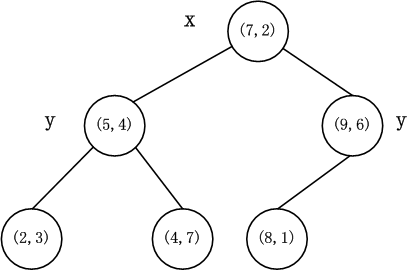
　这里写图片描述

图3 上述实例生成的k-d树
　　注意：每一级节点旁边的’x’和’y’表示以该节点分割左右子空间时split所取的值。
　　
　　 python 实现

from collections import namedtuple
from operator import itemgetter
from pprint import pformatclass Node(namedtuple('Node', 'location left_child right_child')):def __repr__(self):return pformat(tuple(self))def kdtree(point_list, depth=0):try:k = len(point_list[0]) # assumes all points have the same dimensionexcept IndexError as e: # if not point_list:return None# Select axis based on depth so that axis cycles through all valid valuesaxis = depth % k# Sort point list and choose median as pivot elementpoint_list.sort(key=itemgetter(axis))median = len(point_list) // 2 # choose median# Create node and construct subtreesreturn Node(location=point_list[median],left_child=kdtree(point_list[:median], depth + 1),right_child=kdtree(point_list[median + 1:], depth + 1))def main():"""Example usage"""point_list = [(2,3), (5,4), (9,6), (4,7), (8,1), (7,2)]tree = kdtree(point_list)print(tree)if __name__ == '__main__':main()

输出结果：

((7, 2),((5, 4), ((2, 3), None, None), ((4, 7), None, None)),((9, 6), ((8, 1), None, None), None))

k-d树上的最邻近查找算法

　　在k-d树中进行数据的查找也是特征匹配的重要环节，其目的是检索在k-d树中与查询点距离最近的数据点。这里先以一个简单的实例来描述最邻近查找的基本思路。
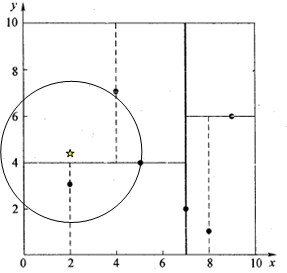
　　星号表示要查询的点 $(2.1,3.1)$ 。通过二叉搜索，顺着搜索路径很快就能找到最邻近的近似点，也就是叶子节点 $(2,3)$ 。而找到的叶子节点并不一定就是最邻近的，最邻近肯定距离查询点更近，应该位于以查询点为圆心且通过叶子节点的圆域内。为了找到真正的最近邻，还需要进行’回溯’操作：算法沿搜索路径反向查找是否有距离查询点更近的数据点。此例中先从 $(7,2)$ 点开始进行二叉查找，然后到达 $(5,4)$ ，最后到达 $(2,3)$ ，此时搜索路径中的节点为<script type="math/tex" id="MathJax-Element-36"><(7,2),(5,4),(2,3)></script>，首先以 $(2,3)$ 作为当前最近邻点，计算其到查询点 $(2.1,3.1)$ 的距离为 $0.1414$ ，然后回溯到其父节点 $(5,4)$ ，并判断在该父节点的其他子节点空间中是否有距离查询点更近的数据点。以 $(2.1,3.1)$ 为圆心，以 $0.1414$ 为半径画圆，如图4所示。发现该圆并不和超平面 $y = 4$ 交割，因此不用进入 $(5,4)$ 节点右子空间中去搜索。

图4 查找

(2.1,3.1) ( 2.1 , 3.1 ) $(2.1,3.1)$ 点的两次回溯判断
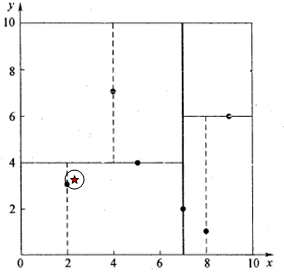
　　再回溯到

(7,2) ( 7 , 2 ) $(7,2)$ ，以

(2.1,3.1) ( 2.1 , 3.1 ) $(2.1,3.1)$ 为圆心，以

0.1414 0.1414 $0.1414$ 为半径的圆更不会与

x=7 x = 7 $x = 7$ 超平面交割，因此不用进入

(7,2) ( 7 , 2 ) $(7,2)$ 右子空间进行查找。至此，搜索路径中的节点已经全部回溯完，结束整个搜索，返回最近邻点

(2,3) ( 2 , 3 ) $(2,3)$ ，最近距离为

0.1414 0.1414 $0.1414$ 。
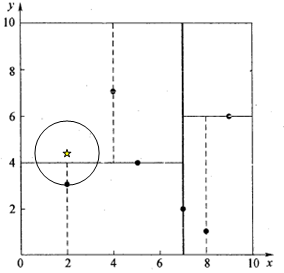
　　一个复杂点了例子如查找点为

(2,4.5) ( 2 , 4.5 ) $(2,4.5)$ 。同样先进行二叉查找，先从

(7,2) ( 7 , 2 ) $(7,2)$ 查找到

(5,4) ( 5 , 4 ) $(5,4)$ 节点，在进行查找时是由

y=4 y = 4 $y = 4$ 为分割超平面的，由于查找点为

y y $y$ 值为

4.5

$4.5$ ，因此进入右子空间查找到

(4,7) ( 4 , 7 ) $(4,7)$ ，形成搜索路径

<(7,2),(5,4),(4,7)>， < ( 7 , 2 ) , ( 5 , 4 ) , ( 4 , 7 ) > ， <script type="math/tex" id="MathJax-Element-60"><(7,2),(5,4),(4,7)>，</script>取

(4,7) ( 4 , 7 ) $(4,7)$ 为当前最近邻点，计算其与目标查找点的距离为3.202。然后回溯到

(5,4) ( 5 , 4 ) $(5,4)$ ，计算其与查找点之间的距离为

3.041 3.041 $3.041$ 。以

(2,4.5) ( 2 , 4.5 ) $(2,4.5)$ 为圆心，以

3.041 3.041 $3.041$ 为半径作圆，如图5所示。可见该圆和

y=4 y = 4 $y = 4$ 超平面交割，所以需要进入

(5,4) ( 5 , 4 ) $(5,4)$ 左子空间进行查找。此时需将

(2,3) ( 2 , 3 ) $(2,3)$ 节点加入搜索路径中得

<(7,2),(2,3)> < ( 7 , 2 ) , ( 2 , 3 ) > <script type="math/tex" id="MathJax-Element-69"><(7,2),(2,3)></script>。回溯至

(2,3) ( 2 , 3 ) $(2,3)$ 叶子节点,

(2,3) ( 2 , 3 ) $(2,3)$ 距离

(2,4.5) ( 2 , 4.5 ) $(2,4.5)$ 比

(5,4) ( 5 , 4 ) $(5,4)$ 要近，所以最近邻点更新为

(2,3) ( 2 , 3 ) $(2,3)$ ，最近距离更新为

1.5 1.5 $1.5$ 。回溯至

(7,2) ( 7 , 2 ) $(7,2)$ ，以

(2,4.5) ( 2 , 4.5 ) $(2,4.5)$ 为圆心

1.5 1.5 $1.5$ 为半径作圆，并不和

x=7 x = 7 $x = 7$ 分割超平面交割，如图6所示。至此，搜索路径回溯完。返回最近邻点

(2,3) ( 2 , 3 ) $(2,3)$ ，最近距离

1.5 1.5 $1.5$ 。
　　这里写图片描述

　　图5 查找

(2,4.5) ( 2 , 4.5 ) $(2,4.5)$ 点的第一次回溯判断
这里写图片描述

图6 查找

(2,4.5) ( 2 , 4.5 ) $(2,4.5)$ 点的第二次回溯判断
k-d树查询算法的伪代码如下：

  算法：k-d树最邻近查找  输入：Kd，    //k-d tree类型  target  //查询数据点  输出：nearest， //最邻近数据点  dist      //最邻近数据点和查询点间的距离  1. If Kd为NULL，则设dist为infinite并返回  2. //进行二叉查找，生成搜索路径  Kd_point = &Kd；                   //Kd-point中保存k-d tree根节点地址  nearest = Kd_point -> Node-data；  //初始化最近邻点  while（Kd_point）  push（Kd_point）到search_path中； //search_path是一个堆栈结构，存储着搜索路径节点指针  If Dist（nearest，target） > Dist（Kd_point -> Node-data，target）  nearest  = Kd_point -> Node-data；    //更新最近邻点  Min_dist = Dist(Kd_point，target）；  //更新最近邻点与查询点间的距离  ***/  s = Kd_point -> split；                       //确定待分割的方向  If target[s] <= Kd_point -> Node-data[s]     //进行二叉查找  Kd_point = Kd_point -> left；  else  Kd_point = Kd_point ->right；  End while  3. //回溯查找  while（search_path != NULL）  back_point = 从search_path取出一个节点指针；   //从search_path堆栈弹栈  s = back_point -> split；                      //确定分割方向  If Dist（target[s]，back_point -> Node-data[s]） < Max_dist   //判断还需进入的子空间  If target[s] <= back_point -> Node-data[s]  Kd_point = back_point -> right；  //如果target位于左子空间，就应进入右子空间  else  Kd_point = back_point -> left;    //如果target位于右子空间，就应进入左子空间  将Kd_point压入search_path堆栈；  If Dist（nearest，target） > Dist（Kd_Point -> Node-data，target）  nearest  = Kd_point -> Node-data；                 //更新最近邻点  Min_dist = Dist（Kd_point -> Node-data,target）；  //更新最近邻点与查询点间的距离的  End while

python实现

def searchTree(tree, data):k = len(data)if tree is None:return [0] * k, float('inf')split_axis = tree['split']median_point = tree['median']if data[split_axis] <= median_point[split_axis]:nearestPoint, nearestDistance = searchTree(tree['left'], data)else:nearestPoint, nearestDistance = searchTree(tree['right'], data)nowDistance = np.linalg.norm(data - median_point)  # the distance between data to current pointif nowDistance < nearestDistance:nearestDistance = nowDistancenearestPoint = median_point.copy()splitDistance = abs(data[split_axis] - median_point[split_axis])  # the distance between hyperplaneif splitDistance > nearestDistance:return nearestPoint, nearestDistanceelse:if data[split_axis] <= median_point[split_axis]:nextTree = tree['right']else:nextTree = tree['left']nearPoint, nearDistanc = searchTree(nextTree, data)if nearDistanc < nearestDistance:nearestDistance = nearDistancnearestPoint = nearPoint.copy()return nearestPoint, nearestDistance

完整代码见github。
寻找 $(2.1,3.1)$ 最近的点：
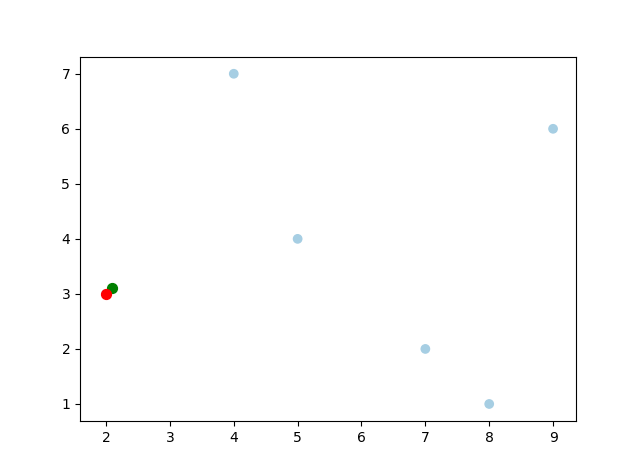
这里写图片描述
寻找 $(2,4.5)$ 最近的点：

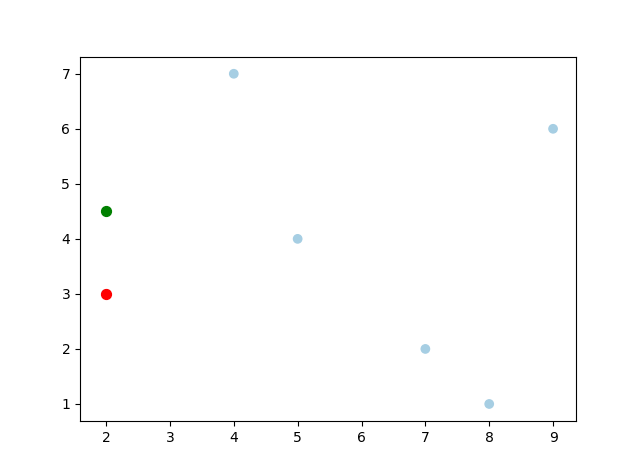
　　上述两次实例，当寻找 $(2.1,3.1)$ 最近的点用时 $0.0$ ，寻找 $(2,4.5)$ 用时 $0.001004934310913086$ 。这表明当查询点的邻域与分割超平面两侧空间交割时，需要查找另一侧子空间，导致检索过程复杂，效率下降。研究表明 $N$ 个节点的 $K$ 维k-d树搜索过程时间复杂度为： $t_{worst}=O(kN^{1-1/k})$ 。
　　

后记

　　以上为了介绍方便，讨论的是二维情形。像实际的应用中，如SIFT特征矢量128维，SURF特征矢量64维，维度都比较大，直接利用k-d树快速检索（维数不超过20）的性能急剧下降。假设数据集的维数为 $D$ ，一般来说要求数据的规模N满足 $N \gg 2D$ ，才能达到高效的搜索。所以这就引出了一系列对k-d树算法的改进。有待进一步研究学习。
　

更多机器学习干货、最新论文解读、AI资讯热点等欢迎关注”AI学院(FAICULTY)”
欢迎加入faiculty机器学习交流qq群：451429116 点此进群
版权声明：可以任意转载，转载时请务必标明文章原始出处和作者信息.
本文转载http://www.cnblogs.com/eyeszjwang/articles/2429382.html ，并做些了修改和补充。

参考文献

[1]. http://www.cnblogs.com/eyeszjwang/articles/2429382.html
[2]. https://leileiluoluo.com/posts/kdtree-algorithm-and-implementation.html
[3]. http://blog.csdn.net/weixin_37895339/article/details/78809528