这个标题描述了一种优化模型或算法,用于在日前电量市场中耦合碳排放权市场、可再生能源绿色证书市场和消纳量市场进行交易的交互式优化。我将解析标题的关键词和概念:
- 日前电量市场:指的是电力市场中进行短期调度和交易的市场,其中电力交易通常提前一天或几天进行。
- 耦合:在这个上下文中,耦合表示将不同市场或交易模块进行整合和协调,使它们在优化模型中相互影响和交互。
- 碳排放权市场:这是一个碳交易市场,其中企业可以买卖碳排放配额或权益,以满足法规或减少碳排放成本。
- 绿色证书市场:绿色证书是由可再生能源发电项目发行的可交易证书,用于证明对可再生能源的投资或使用。
- 消纳量市场:这个市场涉及到可再生能源发电的消纳或接纳情况,即将可再生能源的电量纳入电力系统并分配给消费者或用于满足发电需求。
因此,标题提到的交互式优化是指通过一个综合的优化模型或算法,将碳排放权市场、绿色证书市场和消纳量市场耦合在日前电量市场中进行交易,并在交互过程中实现最优化的决策。优化的目标可能是最大化可再生能源消纳量、最小化碳排放量或实现经济效益的最大化。这样的优化模型可以帮助制定者和参与者在电力系统运营中更好地协调碳减排、可再生能源消纳和市场交易的决策。
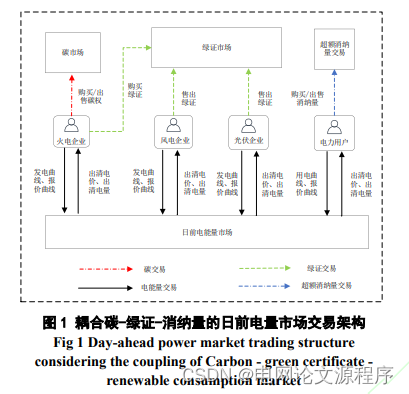
摘要:随着“双碳”目标的提出,电力行业减碳步伐加快,碳交易、绿证交易与超额消纳量交易成为减少碳排放与促进新型电力系统发展的重要市场手段。首先,基于双边集中竞价模式,构建火电、风电、光伏企业与电力用户共同参与的耦合碳-绿证-消纳量的日前电量市场交易机制。其次,兼顾市场成员收益与电量市场社会福利最优目标,建立了上下层迭代交互式交易优化模型。最后,采用交替方向乘子法进行迭代求解,并在IEEE-30节点系统上分析碳配额基准、绿证比例及消纳量交易价格对电量市场出清结果及市场成员收益/成本的影响。算例结果表明,与单一电能量市场交易机制相比,耦合碳-绿证-消纳量的电量市场交易机制能够显著降低火电企业的碳排放量,同时提高风电、光伏企业的中标电量,激励用户跟踪系统新能源出力,减轻系统弃风、弃光现象。
这个摘要描述了一项研究,涉及到电力行业在实现减少碳排放和促进新型电力系统发展的背景下,采用了耦合碳交易、绿色证书交易和超额消纳量交易的日前电量市场交易机制,并建立了相应的交易优化模型。
首先,该研究基于双边集中竞价模式,构建了火电、风电、光伏企业和电力用户共同参与的交易机制。这意味着各类电力企业以及电力用户都可以在该机制中参与交易。
其次,研究考虑到市场成员的收益和电量市场社会福利的最优化目标,建立了上下层迭代的交互式交易优化模型。这意味着市场参与者在交易中既追求自身利益,又考虑整个电量市场的社会效益。
最后,研究采用交替方向乘子法进行迭代求解,并在IEEE-30节点系统上进行了算例分析,评估了碳配额基准、绿证比例和消纳量交易价格对电量市场结果以及市场参与者的收益和成本的影响。
算例结果表明,相较于单一电能量市场交易机制,耦合碳交易、绿证交易和消纳量交易的电量市场交易机制可以显著降低火电企业的碳排放量,提高风电和光伏企业的中标电量,同时激励用户跟踪系统新能源出力,减轻系统弃风和弃光现象。
这项研究的目标是通过优化电量市场交易机制,推动电力行业向低碳发展,最大限度地利用可再生能源,并在市场竞争中实现经济效益和社会效益的双赢。
关键词:碳交易;绿证交易;超额消纳量交易;电量交易; 耦合优化;交互优化;
解读关键词:
-
碳交易:碳交易是一种市场机制,用于减少温室气体排放。在碳交易市场中,参与者可以买卖排放权,即向空气中排放一定数量的温室气体的权利。这种交易机制旨在鼓励减少排放和采用更清洁的能源和生产方式。
-
绿证交易:绿证交易是一种可再生能源交易机制。在这种交易中,可再生能源发电厂生产的每一单位电力都会产生一定数量的绿色证书(绿证),这些证书可以被卖给需要符合可再生能源配额或减排目标的企业或个人。绿证交易市场的目的是促进可再生能源的发展和使用。
-
超额消纳量交易:超额消纳量交易是指将可再生能源电力超过配额的部分进行交易。在可再生能源配额制度下,当电力系统中的可再生能源电力超过政府设定的配额时,这部分超额电力可以以一定价格进行交易,以便更好地利用可再生能源和鼓励清洁能源的发展。
-
电量交易:电量交易是指对电力的买卖交易。这种交易可以在电力市场中进行,参与者可以买入或卖出一定数量的电力。电量交易市场的目的是实现电力供需平衡、提高电力市场竞争效率和促进电力市场的开放与自由化。
-
耦合优化:耦合优化是指将不同的系统、领域或变量之间的相互影响与相互关系纳入考虑,通过综合考虑和最优化方法,使不同系统或领域之间的优化目标得到最佳的协调和平衡。在能源领域,耦合优化可以帮助协调电力系统、能源市场、能源调度等方面的决策和运营。
-
交互优化:交互优化是指在多个参与者之间协同优化决策的过程。在能源领域,特别是电力市场中,多个市场参与者(如发电厂、负荷方、储能设施等)通过相互交互和协商,共同优化决策,以实现整体效益最大化和资源配置的优化。
以上是对关键词的简要解读,这些概念在能源领域和环境政策中具有重要意义,用于推动清洁能源发展、减少碳排放和优化能源系统运营等方面的工作。
仿真算例:选取一天 24 个时段进行日前电量市场出清优 化,采用 IEEE30 节点输电网系统进行仿真分析, 选取母线 4 为参考节点。在日前电量市场发电侧,共有 4 座燃煤电厂,1 个风电场,1 个光伏电站参 与交易。其中,火电 1 碳排放量低,机组电能量成 本较高;火电 2 碳排放量较少,电能量成本较低; 火电 3 机组碳排放系数高,电能量成本较高;火电 4 为碳捕集电厂,其电能量成本最高,包含机组燃 料成本和碳捕集装置运行能耗带来的附加成本, 碳捕集率为 90%,固定能耗为 3MW,捕获单位 CO2 的运行能耗为 0.269MWh/t[39]。由于风电和光 伏具有随机性和波动性,需投入更多的运维费用 和备用成本,风电、光伏的电能量成本高于常规 火电。为了直观体现发电机组特性,列出机组经 济技术参数如附表 B1 所示[22,40-43]。用电侧共有 3 个用户参与日前电量市场交易。各市场交易参数 及 ADMM参数设置见附表 B2。风电、光伏日预测 出力曲线如图 2 所示。根据上述提到的机组碳配额 基准线划分方法,将火电 1、2 划分为 I 类机组, 火电 3 与碳捕集火电 4 划分为 II 类机组,两类机组 执行不同的碳配额基准,碳配额基准及绿证比例 参数见附表 1。由于碳市场交易范围不仅包括电力 行业,还涵盖了航天、钢材等行业,主体数量多, 故本文不考虑火电企业的碳配额供需对碳价的影 响。另外,碳、绿证、可再生能源配额考核均以 年为履约期,发电商、用户可以在全年不同交易 时段购买或卖出碳配额、绿证、消纳量,但全年 中碳配额、绿证、消纳量交易产生的成本都能够 分摊到机组和用户的电量中,对每 1 度电成本产生 影响。不失一般性,本文碳、绿证、消纳量市场 价格采用年度交易均价,考虑碳、绿证等市场的 交易时间尺度能够涵盖日前市场时间尺度,分析 1 天中碳、绿证、消纳量交易对电量市场的影响。
仿真程序复现思路:
根据以上描述,可以将仿真复现分为以下几个步骤,并使用程序语言进行表示:
-
定义电力系统和节点信息:选择IEEE30节点输电网系统,并选择母线4为参考节点。定义节点的输电网拓扑结构、电力负荷和发电机组等相关信息。
-
定义发电侧参与交易的电力源:在日前电量市场发电侧,共有4座燃煤电厂、1个风电场和1个光伏电站参与交易。根据描述中的经济技术参数,定义各个发电机组的碳排放量、电能量成本等信息。
-
定义用电侧参与交易的用户:确定用电侧共有3个参与日前电量市场交易的用户,定义其电力需求和交易参数。
-
定义市场交易参数:根据描述中提到的附表B2,定义各个市场交易的参数,包括碳配额基准、绿证比例和ADMM算法的参数设置。
-
定义风电和光伏的日预测出力曲线:根据描述中提到的图2,定义风电和光伏电站的日预测出力曲线,考虑其随机性和波动性。
-
进行碳配额基准划分和碳、绿证、消纳量交易:根据描述中提到的碳配额基准线划分方法,将发电机组划分为不同的类别,并执行不同的碳配额基准。考虑碳、绿证、消纳量在全年不同交易时段的购买和销售情况,分析其对电量市场的影响。
-
进行电量市场出清优化:选取一天24个时段进行日前电量市场出清优化,根据市场交易参数和各参与方的需求,使用优化算法(如线性规划或基于价差的方法)对电量市场进行出清优化,以实现整体效益的最大化。
具体的程序实现方式可以根据所选择的编程语言和优化库来进行。下面是一个示例,使用Python和Pyomo库进行线性规划优化的表示:
import numpy as np
from scipy.optimize import minimize# 定义问题参数
n_generators = 6 # 发电侧的机组数量
n_consumers = 3 # 用电侧的用户数量
n_timesteps = 24 # 时间步数# 定义机组参数
costs = np.array([10, 5, 12, 20, 8, 8]) # 机组电能量成本
emissions = np.array([1, 0.5, 1.5, 2, 0.8, 0.8]) # 机组碳排放量
...# 定义用户参数
demands = np.array([50, 30, 20]) # 用户需求
...# 定义ADMM参数
rho = 0.1 # 步长参数
max_iterations = 100 # 最大迭代次数
tolerance = 1e-6 # 收敛容差# 定义ADMM更新函数
def admm_update(lambda_, mu):# 定义发电侧机组的优化问题def generator_optimization(x):# 目标函数:最小化总成本total_cost = np.sum(costs * x)# 约束:需求满足demand_constraint = np.sum(x) - np.sum(demands)# 约束:碳排放满足emission_constraint = np.sum(emissions * x) - np.sum(lambda_)# 目标函数和约束条件构建return total_cost + np.dot(mu, [demand_constraint, emission_constraint])# 优化求解发电侧机组的最优解optimization_result = minimize(generator_optimization, np.zeros(n_generators), method='SLSQP')# 更新发电侧机组的操作变量generator_operations = optimization_result.x# 更新用电侧的操作变量consumer_operations = demands + mu[0] / rhoreturn generator_operations, consumer_operations# 初始化ADMM变量
lambda_ = np.zeros(n_consumers) # 用于存储乘子变量
mu = np.zeros(1) # 用于存储ADMM增广变量# 迭代优化过程
for timestep in range(n_timesteps):# 更新发电侧机组的预测出力generator_forecasts = np.zeros(n_generators) # 根据实际需求更新预测出力# 执行ADMM的迭代过程converged = Falseiteration = 0while not converged and iteration < max_iterations:# 保存前一次的操作变量generator_operations_prev = generator_operations.copy()consumer_operations_prev = consumer_operations.copy()# 执行ADMM更新步骤generator_operations, consumer_operations = admm_update(lambda_, mu)# 更新乘子变量和增广变量lambda_ += rho * (consumer_operations - demands)mu += rho * (np.sum(generator_operations) - np.sum(consumer_operations))# 判断收敛性if np.linalg.norm(generator_operations - generator_operations_prev) < tolerance and \np.linalg.norm(consumer_operations - consumer_operations_prev) < tolerance:converged = Trueiteration += 1# 输出最优解print(f"Time Step: {timestep + 1}")print("Generator Operations:", generator_operations)print("Consumer Operations:", consumer_operations)# 绘制结果等
...
注意,这只是一个伪代码示例,无法直接运行。你需要根据具体问题进行调整和扩展,如添加实际机组和用户的参数、预测出力曲线的更新方法、结果的输出和可视化等。此外,你可能要选择适合你问题的优化方法和库。
此示例提供了一个基本的ADMM算法的框架,以帮助你开始编写仿真程序。根据问题的复杂性,你可能需要进行更多的调整和优化。 同时,请注意可能的数值稳定性问题,并根据需要增加异常处理和边界条件的代码。